基于聚类算法的脉冲电压绝缘老化实验漏电流检测方法

蒋存波，王西乐，焦 阳，杨家志，王怀红，孔祥丽

(桂林理工大学信息科学与工程学院，广西桂林 541004)

基于聚类算法的脉冲电压绝缘老化实验漏电流检测方法

蒋存波，王西乐，焦 阳，杨家志，王怀红，孔祥丽

(桂林理工大学信息科学与工程学院，广西桂林 541004)

在绝缘加速老化实验中，一般将漏电流作为绝缘失效的判别标准。为了从回路电流检测信号中去除电容过渡过程电流从而获得漏电流值，设计一种基于相邻采样点距离进行漏电流判别的聚类分析算法。在双极性高频方波脉冲下电容过渡过程电流主要集中于方波脉冲边沿5τ以内，10τ后过渡过程基本结束，此后试样的回路电流可看为漏电流。据此电流变化过程及对应的数值关系，采用聚类分析的方法从采样周期数据中分类出漏电流数据，最后对漏电流数据求取平均值。仿真结果表明，在采样周期为51个以上时，采用该聚类分析算法得到的漏电流检测值相对误差在2%以内，可以有效去除电容过渡过程电流和随机噪声对漏电流检测的影响，较好地满足脉冲电应力绝缘寿命加速老化实验的要求以及提高实验结果的可靠性。

漏电流检测;聚类分析;绝缘寿命

0 引言

为了快速获取电气绝缘材料/绝缘系统(EIM/ EIS)的绝缘状态和寿命信息，目前主要采用的是对试样加速老化的方法。在EIS(EIM)加速老化实验中，一般通过漏电流值进行绝缘失效判别［1－3］。因此漏电流值的准确性对绝缘失效判别和剩余寿命的预估非常重要。由于试样和电极对之间具有电容特性，在PWM脉冲激励下，直接用回路电流作为试样漏电流存在较大的误差。为了实验结果的准确性与可靠性，需要从回路电流中检测出漏电流。使用硬件电路的方法虽然可以从试样回路电流中分离出漏电流，但由于电路较为复杂，难以满足绝缘老化实验长期稳定运行的需要。本文介绍一种利用聚类分析的软件方法，可以从回路电流中分离出漏电流，简化了硬件电路，满足长期稳定运行的需要［4－5］。

1 漏电流检测的实验方法

针对绝缘寿命老化实验，给出其等效模型，在实验模型的基础上，对电路的电流特征进行分析，提出解决思路，然后给出取样电阻电压表达式和A/D采样电路。

1.1 实验主回路模型及电流特征

依据电机绝缘寿命实验标准［6－7］，选择上升沿0.04～1μs、频率为1～20 kHz、脉冲幅值300～3 000 V的双极性方波脉冲源来进行加速老化实验。实验主回路主要由双极性方波脉冲电源UM、限流电阻RX、试样S和取样电阻RT构成。其实验原理如图1所示。

图1中的试样S由上下电极和中间的绝缘薄膜组成。根据已有的研究成果，试样S可由等效电容C与绝缘电阻RLS并联表示［8］。其等效模型图如图2所示。

图1 实验原理图Fig.1 Experimental principle

图2 等效模型图Fig.2 Equivalentmodel

等效电容C范围在100～2 000 pF;绝缘电阻RLS范围为0.38～100 MΩ。在实验中取双极性脉冲电源的幅值为UM=640 V，频率f=20 kHz，限流电阻RX=750Ω，取样电阻RT=2Ω。试样回路的RC时间常数为

由上述等效模型可以计算出回路时间常数10－9s≤τ≤10－7s，τ＜T(T为双极性脉冲电源周期)。定义稳态时回路电流Icof:

此时电路电流时域响应表达式如下:

①电容电流为

③回路电流为

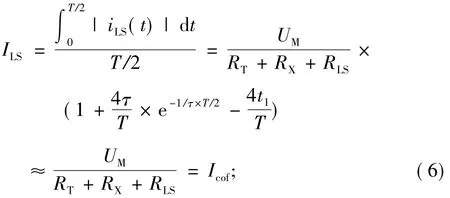
在有噪声情况下回路电流表达式为

图3 电流曲线图Fig.3 Current curve

式中:ε(t)为白噪声函数，且E(ε(t))=0。在电压UM=640 V、频率f=20 kHz、限流电阻RX=750 Ω、取样电阻RT=2Ω时，实际测得的0.025 mm的聚酰亚胺绝缘薄膜试样的回路电流波形如图4所示。

图4 采样点分布图Fig.4 Sampling points distribution

根据电流表达式(1)～(3)和电流曲线图3可以看出，单个周期的电流特征(［0，T/2］内):

1)在电容过渡过程时间tw(tw≈5τ)内电容过渡过程电流以时间常数τ为指数进行衰减［9］。

2)从图3b和式(6)可以看出，在tw时间后电容过渡过程电流趋向于0，此时回路电流的主要成分为漏电流。对于［T/2，T］区间，其变化特征与［0，T/2］相同。

绝缘老化是一个渐进的随机过程，随着老化程度的增加，漏电流稳定缓慢增大;但在单个脉冲内，由于脉冲时间短，漏电流几乎不变。在老化程度加剧后、绝缘失效前，漏电流会产生波动，局部放电现象明显增多。

根据单个周期内的电流特征，为了消除电容过渡过程电流的影响，使用一种基于聚类分析的方法把回路电流采样点分类得到漏电流数据。为了消除单个周期内回路电流值略微下降而造成的漏电流下降假象，采用求取多个周期漏电流平均值的方法，对漏电流数据滑动求取每个观察区间内多个周期的漏电流均值，从而得到较为准确的漏电流检测值，同时减少了计算量。另外对于白噪声的干扰，根据式(7)，对多个周期的统计数据求均值亦可有效消除。

1.2 漏电流检测A/D采样电路

本漏电流检测A/D采样电路图如图5所示。

图5 A/D采样电路图Fig.5 A/D sampling circuit

取样电阻 RT将回路电流 ii(t)转换为电压Ut(t)=ii(t)×RT，放大倍数为K，故Uo(t)=K× UT(t)=K×RT×ii(t)。限幅电路后的输出信号为－5 V≤Ulim(t)≤5 V。本实验中取K=20，RT=2 Ω。绝对值电路的输出信号Uab(t)为

由以上的分析可知，对于稳定过程来说，ii(t) =iLS(t)，且由于其取样电阻两端电压UT(t)5 V，故在经过放大电路和限幅绝对值电路后输出信号Uab(t)=|K×RT×ii(t)|=|K×RT×iLS(t)|。从采样数据中分类出稳定过程的采样数据，对其除以K×RT，即可得到漏电流值。由于绝对值电路和输入模拟信号在［0，T/2］与［T/2，T］的对称性，采样数字信号数据的波形周期为原方波脉冲的一半。下文中采样周期即为数字信号波形的周期。

2 漏电流检测算法思想与描述

2.1 聚类算法思想

根据第1.1节的电流特征及分析，提出一种基于相邻点的距离对采样数据进行聚类分析的思路。先计算出距离阈值，根据相邻采样点间的距离确定该点是否为漏电流采样点并按照规则对非漏电流采样点进行填充，然后在观察周期内进行统计平均求取漏电流值。该思路的重点是确定距离阈值和采样数据的分类和填充。

本算法选用绝对距离，非漏电流采样点选用上一个采样周期的均值填充。相邻采样点的绝对距离大于距离阈值，则该采样点分为漏电流类;否则为非漏电流类，按规则进行填充。

本算法针对原始采样点，先求出采样波形的频率和一个周期的采样点个数;然后以每50个采样周期为一个观察区间，在每个采样周期内对采样点进行聚类划分，求出每个采样周期的漏电流均值。然后求出本次观察区间的漏电流均值;把观察区间的采样数据左移一个采样周期，新加一个采样周期的数据，重复上述程序得到下一个采样周期的漏电流均值;对于每个新到的采样周期数据，重复上述操作。

为了描述的方便，先给出一些变量概念:

(a)最大值Max:采样得到的数据中的最大值。

(b)最大值位置Pos:在本算法中该位置指的是在采样数据数组中该点的值为Max，且其在数组中的前一个数据的值不是Max。

(c)采样间隔时间ΔT:当采样频率为2 MHz时，其值为5×10－7s。

(d)一个采样周期的采样间隔数intervalNum:两个相邻最大值位置(Pos)之间的采样点个数，值为两个相邻最大值位置的差。

(e)漏电流平均值数组I［50］:记录每个周期漏电流的平均值Ii(i为1，2，…，50)，连续求50个采样周期，并将每个周期的结果存入此数组中。

(f)漏电流检测值数组ILS［50］:记录每个周期的漏电流检测值ILSi(i为1，2，…，50)。对于ILSi，值为I1，I2，…，Ii的均值。

(g)两相邻采样点间的距离Dis(Di，Di+1):两个相邻采样点的距离，值为|Di－Di+1|(i=1，2，…，m)。

(h)最小值Min:一个采样周期内采样数据的最小值，在有无噪声影响下，其均出现在稳定过程中;在有噪声情况下，其每个采样周期的值可能不同。

(i)距离阈值DisThreshold:定义为最小值与其左右相邻点的距离的较小值。

2.2 算法描述

①对于采样数据数组，求出其最大值Max。

②在数组中，求出其相邻的2个最大值位置，记为Pos1，Pos2。然后求出intervalNum=Pos2－Pos1。据此，可求出方波脉冲源的频率为fsquare=1/ (2×intervalNum×ΔT)。

③从采样数据数组中选取连续的1个波形周期的数据，可从任意数据开始，特殊的也可以从出现的第一个最大值位置开始，数据个数为interval-Num+1。组成新的数组U［interval+1］。

④对于数组 U［interval+1］，求出其最小值Min，然后求取其距离阈值DisThreshold。

⑤对于数组U［interval+1］，求出其每两个相邻元素的距离 Dis(Ui，Ui+1)。若 Dis(Ui，Ui+1) ＞DisThreshold，按规则填充对应点至数组ULS中;反之，把元素Ui和Ui+1添加到漏电流数据数组ULS中，注意当有连续元素满足和连续元素不满足时，均不重复添加。

⑥对数组U［interval+1］遍历结束后，对数组ULS求平均值，即为I1。

⑦选取下一个采样周期数据，重复上述步骤④～⑥，得到漏电流均值I2、I3、…、I20;对数组I［50］取平均值，求出该观察区间的漏电流检测值ILS1。

⑧把I［50］左移一位，即I1←I2、I2←I3，…，I49←I50。添加新的采样周期数据到U［interval+ 1］，重复步骤④ ～⑥，记漏电流平均值为I50。对数组I［50］取平均值，求出下一个观察区间的漏电流检测值ILS2。相似的，可求出漏电流检测值ILS3、ILS4、…、ILSn。

依据上述思想，该算法流程图如图6所示。图6a说明了如何对数据进行聚类，图6b说明了如何用统计的方法求观察区间内的漏电流值。

3 算法仿真与结果分析

采用Matlab R2012(a)对实验主回路和漏电流检测A/D采样电路进行仿真，得出采样数据;然后用VS2010编写漏电流检测的聚类分析算法，对采样数据进行处理，得出漏电流均值;最后把漏电流均值导入Excel 2007中，输出散点图。本实验的Matlab电路仿真图见图7。

在无噪声时，仿真条件如下:极性方波脉冲源的幅值640 V，频率为20 kHz;放大倍数K=20;限幅为5 V;ADC采样位数为12位，采样频率为2 MHz，一个采样周期为500 ns。RX=75Ω，RT=2 Ω，RLS=0.5 MΩ，C=500 pF。根据上述仿真图，用Matlab仿真后得到的电流原始采样数据如图8a所示。针对该采样数据，在VS2010中经过本文算法处理后，用Excel绘出散点折线图如图8b所示。

图6 算法流程图Fig.6 Algorithm flow chart

图7 Matlab实验电路仿真图Fig.7 Experiment circuit simulation by Matlab

经实验测试，用示波器测得的噪音幅值不超过10 V，故选择噪声源幅值为10 V;其他条件与无噪声情况下相同。根据实验仿真图 (图7)，用Matlab仿真得到的部分原始采样点如图9a所示。对于有噪声情况的采样点，在VS2010中经过本文算法处理后得到的漏电流检测值以及相对误差如图9b和图9c所示。

根据上述仿真结果，可以有如下结论:

(1)无噪声情况。无噪声情况下的漏电流信号为真实的漏电流信号。由于仿真条件下绝缘电阻的值是恒定的，故每个周期的漏电流均值都相同，为ILS。从图8b可以看出，原始采样点经过算法处理后的漏电流检测值为一条直线，与图中黑色直线所示的漏电流理论值波形相符。

由于ADC的分辨率，采样存在一定的固有误差，这点在图8b中可以清晰地反映出来。

在本文给定的仿真条件下，一个采样周期内漏电流的理论平均值为

由于ADC采样器的分辨率，造成其漏电流相对误差为

δ=(1.282－1.278)/1.278=0.31%。

图8 无噪声的漏电流仿真分析图Fig.8 Simulation analysis of leakage current under no-noise condition

(2)有噪声情况。在有噪声的情况下，从图9b可以看出采用本算法得到的漏电流检测值接近漏电流理论值，并且运行时间越长，采样个数越多，最终得到的漏电流检测值越能消除随机噪声的影响。从图9c中可以得到，在该仿真条件下，采样周期个数大于51时，得到的漏电流检测值的相对误差小于2%。此误差可以满足文献［8］中相对偏差率小于3.03%要求。

因此，本算法在有噪声的情况下亦可以很好地检测出漏电流值，并且采样的时间越长，输出的漏电流值更加精确，消除了随机噪声对漏电流的干扰。

4 结束语

本文将聚类分析算法应用于绝缘寿命老化实验的漏电流检测中，该算法首先确定了采样周期的频率，然后根据相邻采样点间的距离和距离阈值从采样周期内的数据中分类出漏电流数据，对其求均值，通过多个周期漏电流均值的相加求平均，消除了随机噪声对实验电路的影响。仿真实验表明:采用该算法的漏电流检测值非常接近漏电流的理论均值，在有噪声情况下，其相对误差仍可小于2%。与文献［8］相比，在满足应用精确度要求的情况下，该算法简化了硬件电路设计，满足长期稳定运行的需求。但这只是对预老化过程中噪声影响下漏电流检测的初步探索，对于具体噪声下的电流变化过程及绝缘逐渐失效时噪声对漏电流的影响还有待进一步研究。

图9 有噪声的漏电流仿真分析Fig.9 Simulation analysis of leakage current under noise condition

［1］蒋存波，曾莎，闫军部，等．一种绝缘寿命测试用高压方波脉冲电源的研制［J］．电测与仪表，2012，49(9):91－96．

［2］周力任，吴广宁，高波，等．聚酰亚胺薄膜中电荷输运机理和空间电荷特性［J］．电工技术学报，2009，24(12): 6－11．

［3］Wheeler JCG．Effects of converter pulses on the electrical in-sulation in low and medium voltagemotors［J］．IEEE Electrical Insulation Magazine，2005，21(2):22－29．

［4］孙吉贵，刘杰，赵连宇．聚类算法研究［J］．软件学报，2008，19(1):48－61．

［5］公茂果，王爽，马萌，等．复杂分布数据的二阶段聚类算法［J］．软件学报，2011，22(11):2760－2772．

［6］周凯，吴广宁，雷克刚，等．脉冲电压下局部放电对聚酰亚胺膜寿命的影响［J］．材料科学与工程学报，2008，26 (3):361－364．

［7］Mazzanti G，MontanariG C，Dissado L A．A space-charge life model for ac electrical aging of polymers［J］．IEEE Transactions on Dielectrics and Electrical Insulation，1999，6(6): 864－875．

［8］蒋存波，项春雷，杨家志，等．基于方波脉冲电压绝缘寿命实验的漏电流检测［J］．电测与仪表，2014，51(18): 68－72．

［9］知田．RC、RL和RCL电路中的过渡过程 (状态)规律［J］．家电检修技术，2004(9):26－27．

Leakage current detection method in insulation aging experiment under pulse power based on cluster algorithm

JIANG Cun-bo，WANG Xi-le，JIAO Yang，YANG Jia-zhi，WANG Huai-hong，KONG Xiang-li (College of Information Science and Engineering，Guilin University of Technology，Guilin 541004，China)

The leakage current is taken as discrimination standard for insulation failure in insulation accelerated experiment．In order to obtain the leakage currentby removing the capacitor transient current from the loop current detection signal，a cluster analysis algorithm thatmakes decision by use of the distance between neighbor sampling points is designed．Capacitor transient current ismainly concentrated in the time of square pulse edge’0～5τin the high-frequency bipolar pulse power accelerated aging experiment．The transient process is finished basically within 10τand the loop current of samplemay be regarded as the leakage current after that．Based on the current variety process and the corresponding numerical relations，cluster analysis can classify the leakage current data from the sampling period data and calculate themean value of the leakage current data．The simulation results prove that on under this conditin the sampling periods aremore than 50，the biggest relative error of the acquired leakage current by the cluster analysis algorithm is 2%．Thus it can eliminate the effect of capacitor transient process current and random noise on detection of leakage current effectively，meet the requirement of accelerated aging experiment under pulse electrical stresswell and improve the reliability of the experiment result．

leakage current detection;cluster analysis;insulation aging

TP206.3

:A

2015－08－20

国家自然科学基金项目(51167004);广西自然科学基金项目(2011GXNSFA018022;2013GXNSFBA019250);专利支持项目(KY2015ZL100)

蒋存波(1962—)，男，教授，研究方向:嵌入式系统及应用、自动检测与控制装置、计算机应用，jiangcunbo@163.com。

蒋存波，王西乐，焦阳，等．基于聚类算法的脉冲电压绝缘老化实验漏电流检测方法［J］．桂林理工大学学报，2016，36(4):823－829．

1674－9057(2016)04－0823－07

10.3969/j．issn.1674－9057.2016.04.030