卵形弹体侵彻预开孔靶理论分析*

邓佳杰,张先锋,乔治军,2,郭 磊,何 勇,陈东东

(1.南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094;2.中国人民解放军95856部队，江苏 南京 210000)

卵形弹体侵彻预开孔靶理论分析*

邓佳杰1,张先锋1,乔治军1,2,郭 磊1,何 勇1,陈东东1

(1.南京理工大学智能弹药技术国防重点学科实验室，江苏 南京 210094;2.中国人民解放军95856部队，江苏 南京 210000)

以破爆型串联战斗部后级随进弹对预开孔靶侵彻过程为研究对象，基于锥形预开孔和库仑摩擦模型，发展完善了包括扩孔/开坑和稳定侵彻的卵形弹体侵彻预开孔靶理论模型。分别对该模型在侵彻脆性和弹塑性靶体的有效性进行了实验验证。利用该模型分析了弹头曲径比、预开孔直径、预开孔形状等对侵彻结果的影响。研究结果表明：发展完善的模型计算结果与实验数据吻合较好。柱形开孔情况下，侵彻速度、弹头曲径比及相对孔径同侵彻深度呈正比；在侵彻容积相同的条件下，弹体侵彻预开锥孔的侵深结果与锥角及相对入孔孔径变化关系较大。

爆炸力学；侵彻深度；空腔膨胀理论；预开孔靶体；串联战斗部

破爆型串联战斗部是毁伤坚固目标最有效的武器之一。串联战斗部后级随进弹沿前级聚能装药预开孔道侵入靶体内部爆炸，相对同口径动能战斗部具有更好的毁伤目标能力。串联战斗部对目标的毁伤效能取决于后级随进弹的侵彻深度，随进动能弹侵彻预开孔靶体的能力是实现串联战斗部毁伤效能的关键所在。因此，研究弹体侵彻预开孔靶过程具有重要意义。

针对破爆型战斗部后级随进弹侵彻过程已有大量研究，J.A.Teland[1]应用空腔膨胀理论分析了预制孔侵彻问题，得到了预测随进侵彻深度公式；张雷雷等[2]在Teland理论基础上，引入靶体损伤系数修正了侵彻深度计算公式；王树有[3]针对不同头形弹体、靶体孔形、靶体损伤类型等对后级随进侵彻进行了较细致的研究，并得到了相应的理论模型；王静等[4]对不同预开孔孔径的侵彻问题进行了数值计算，并重新定义了Teland模型中靶体阻力参量；文鹤鸣等[5]提出后级随进侵彻的四阶段模型，进一步修正Teland理论；Jr.E.N.Folsom[6]在低速侵彻预开孔混凝土靶实验基础上引入经验常数，改进ACE经验公式；F.J.Mostert等[7]通过预开孔靶低速侵彻实验及数值模拟，验证了其预开孔混凝土侵彻模型。目前，大部分关于预开孔靶侵彻的研究未考虑侵彻过程中的扩孔/开坑阶段，且对侵彻速度、弹体头部几何尺寸、靶体开孔形式等影响侵彻结果的因素研究较少。模型适用性较低，难以真实反映随进动能弹对预开孔靶的侵彻过程，对破爆型串联战斗部的优化设计指导意义有限。

本文中综合考虑侵彻过程的扩孔/开坑和稳定侵彻阶段、弹体头部摩擦阻力及与实际射流开孔近似的理想锥形预开孔，借助球形空腔膨胀理论，发展一种卵形弹体侵彻预开孔靶理论模型，同时开展相关实验，结合已有实验数据，验证模型适用性。在此基础上，分析侵彻速度、弹头曲径比、孔径对预开孔靶侵彻深度的影响。并结合射流开孔孔形的研究成果，分析弹体侵彻典型锥形预开孔靶体的侵彻性能。

1 卵形弹体侵彻预开孔靶体模型

1.1 弹体侵彻预开孔靶过程及相关参数

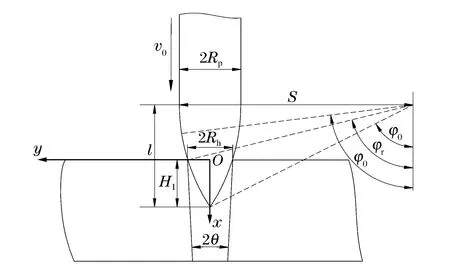
图1 弹体与预开孔靶参数的定义Fig.1 Parameter definition of projectile and pre-drilled target

弹体侵彻预开孔靶过程可分为扩孔/开坑和稳定侵彻两个阶段。分析弹体侵彻预开孔靶作用过程，假设射流开孔孔形为理想锥形；弹体垂直侵彻且弹体轴线与预开孔孔径中心无弹道误差；考虑弹体头部摩擦力，弹靶间摩擦力采用库仑摩擦形式，动摩擦因数的选取参考已有文献数据并结合预开孔侵彻模型；弹体为刚性，侵彻过程中无变形及质量侵蚀。

以靶体迎弹面与弹轴交汇点为坐标原点，弹体沿x轴正向侵彻，建立如图1所示的几何关系。模型所涉及的参数定义如下：l为弹体头部长度；Rp为弹体半径，d=2Rp；S为头部圆弧半径；φ0为弹尖处圆弧段圆心角，φ0=sin-1[(S-Rp)/S]；φr为圆弧段与靶体表面接触位置圆心角；φ为圆弧段与靶体接触任意位置圆心角；Rh为靶体预开孔入孔半径；弹头曲径比为S/d；2θ为靶体预开孔锥角，θ=0为柱形预开孔；H1为弹体从侵入靶体孔道至接触靶体的距离；H2、H3分别为两阶段侵彻深度；H为弹体最终的侵彻深度，H=H1+H2+H3。

1.2 空腔膨胀理论靶体响应力模型

从基本的守恒方程和连续介质力学原理出发，根据球形空腔膨胀达到稳定后的弹塑性区域及靶体材料的本构关系，获得弹体头部响应力与空腔膨胀速度的二次函数关系[8]：

σr=A+Bv2

(1)

式中：A、B为与靶体材料相关的常数项,v为空腔膨胀速度。根据任意位置的头部圆弧段与靶体接触圆心角φ，可确定稳定侵彻阶段瞬时轴向速度vx处弹体表面法向应力

σn=A+B(vxcosφ)2

(2)

M.J.Forrestal等[9-10]在对弹体侵彻混凝土和铝材料研究基础上，分别提出脆性材料和弹塑性材料的靶体响应力表达式。

脆性材料(混凝土、岩石、陶瓷等脆性材料)

(3)

式中:fc为靶体无围压强度,Sc为靶体静阻力分量,ρt为材料密度。

理想弹塑性材料(金属材料)

(4)

式中:σs为靶体静阻力,E为弹性模量,Y为屈服强度,n为应变硬化指数。

1.3 卵形弹体侵彻预开孔靶过程分析模型

1.3.1 第1阶段(侵彻扩孔/开坑阶段)

该阶段靶体在压应力作用下向最小抗力方向产生塑性流动，靶体自由面产生延性扩孔/锥形开坑，靶体孔道大于弹径。该阶段的初始及终了条件为：H1≤x≤H1+H2，v1≤vx≤v0。

在进入扩孔/开坑阶段前，弹体以恒定速度侵入靶体孔道一定深度直至弹靶接触，该深度与弹体头部几何尺寸及预开孔孔径有关，即

(5)

根据对脆性材料开坑区确定方法的研究结果[11-13]，并结合文献[6]中侵彻不同孔径预开孔混凝土靶的开坑崩落实验现象，假设该阶段侵彻预开孔靶深度与2倍弹径成正比且与预制孔孔径变化有关，即

(6)

由于扩孔/开坑阶段历时较短，为保证两阶段弹体受靶体阻力的连续性，可视扩孔/开坑阶段弹体表面法向应力同侵彻深度呈线性关系变化，即

(7)

式中:σn为稳定侵彻阶段表面法向应力，遵循空腔膨胀理论。

弹体表面位置角dφ对应的弹头表面力为:

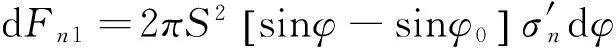
(8)

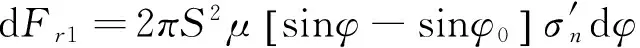
(9)

(10)

故瞬时侵彻深度x处弹体表面阻力为:

(11)

式中:μ为弹靶间动摩擦因数；弹头圆弧段与靶体接触范围[φ1,φ2]由该阶段侵彻深度及弹靶几何关系确定，瞬时侵深x处的锥形开孔截面半径ah为:

(12)

瞬时侵深x处的弹靶接触部分头部圆弧段与靶体初始接触位置圆心角φ1为:

(13)

圆心角φ2为弹体头部圆弧段与靶体最后接触位置对应的角度，即

(14)

由式(11)～(14)，得到侵彻阻力关于瞬时侵彻速度vx及对应瞬时侵彻深度x的函数值F1(vx,x)。根据F1(vx,x)=-ma=-mvxdvx/dx，可得到第1阶段瞬时侵彻速度与侵彻深度的关系：

(15)

式中:v1为该阶段结束时刻的瞬时速度。

1.3.2 第2阶段(稳定侵彻阶段)

稳定侵彻阶段靶体仅沿径向运动，符合球形空腔膨胀理论规律，此阶段侵彻孔道直径与弹径相等。该阶段的初始及终了条件为：H1+H2≤x≤H1+H2+H3，0≤vx≤v1。

稳定侵彻阶段瞬时侵彻深度x处弹体表面阻力为

(16)

由F2(vx,x)=-mvxdvx/dx及该阶段的边界条件，得到如下关系:

(17)

式中:H3为该阶段的侵彻深度。最终的侵彻深度H由式(5)～(6)和(17)得到。

2 分析模型的实验验证

2.1 无预开孔半无限靶侵彻

在上述理论模型推导的基础上，利用已有半无限铝靶和混凝土靶侵彻实验，验证在预开孔孔径Rh=0(即无预开孔靶侵彻情况)的特殊情况下理论模型的适用性。

2.1.1 铝靶

计算采用6061-T6511侵彻实验数据[14]。弹体质量m=20.5 g，半径Rp=3.555 mm，头部长度l=11.8 mm，头部圆弧半径S=21.33 mm，弹头曲径比为3。靶体密度ρt=2.71 g/cm3，弹性模量E=69 GPa，屈服强度Y=276 MPa，应变硬化指数n=0.072，弹靶间动摩擦因数μ=0.03[15]。由图2可见，该模型的预估侵彻深度与实验数据吻合较好。相对于Forrestal模型而言，本文中模型综合考虑了侵彻扩孔/开坑阶段，较好地诠释了弹体侵彻全过程。

2.1.2 混凝土靶

模型采用M.J.Forrestal等[16]的实验结果。弹体质量m=1.6 kg，半径Rp=15.25 mm，头部长度l=50.5 mm，头部圆弧半径S=91.5 mm，弹头曲径比为3。靶体密度ρt=2.26 g/cm3，无围压强度fc=51 MPa，弹靶间动摩擦因数μ=0.05[13,17]。由图3可见，模型预估与实验结果吻合较好。

图2 6061-T6511靶侵彻数据与理论模型预估Fig.2 Experiment and theory results of 6061-T6511 target

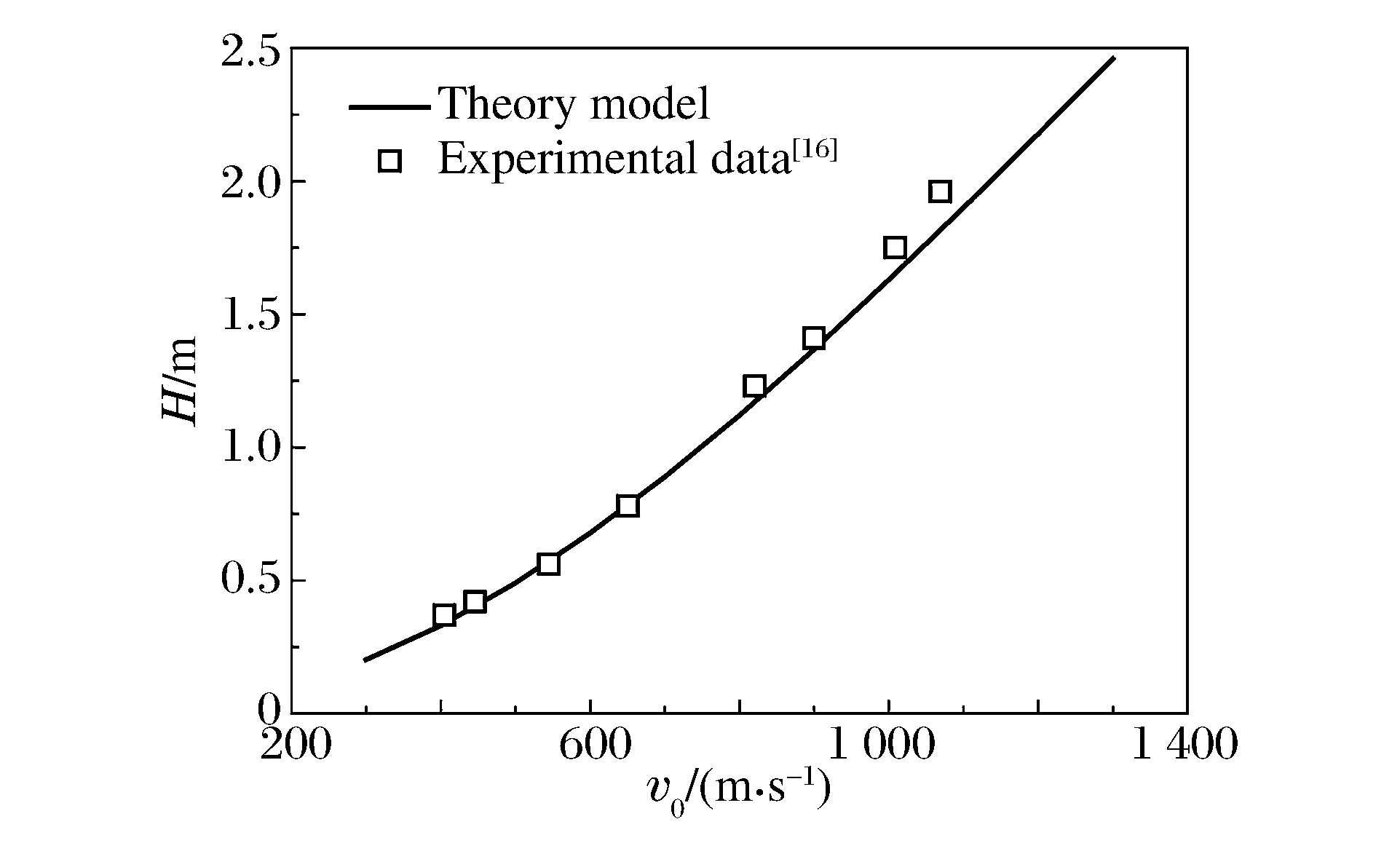
图3 混凝土靶侵彻数据与理论模型预估Fig.3 Experiment and theory results of concrete target

2.2 预开孔半无限靶侵彻

图4 实验弹外形图Fig.4 Photo of actual oval-nosed projectile

为确定卵形弹体侵彻预开孔靶模型的有效性，开展卵形弹体侵彻预开柱孔靶实验。如图4所示，弹体材料为30CrMnSiNi2A，直径14.5 mm，质量m=67 g，头部长度l=24.05 mm，头部圆弧半径S=43.5 mm，弹头曲径比为3。靶体为2024铝，直径100 mm，密度ρt=2.71 g/cm3，弹性模量E=70 GPa，屈服强度Y=320 MPa，应变硬化指数n=0.05，弹靶间的滑动摩擦因数μ=0.03[15]，如图5所示，靶体中心预制有3种不同尺寸的预开柱形孔。

图5 实验前后靶体实物图Fig.5 Photographs of 2024 aluminum targets

表1给出了实验侵彻深度与模型计算结果的对比值。由表1可知，实验结果与理论计算的相对误差在9%以下，模型预估与实验结果吻合较好，以上实验验证表明：预开孔侵彻理论分析模型能够较准确地计算侵彻深度。

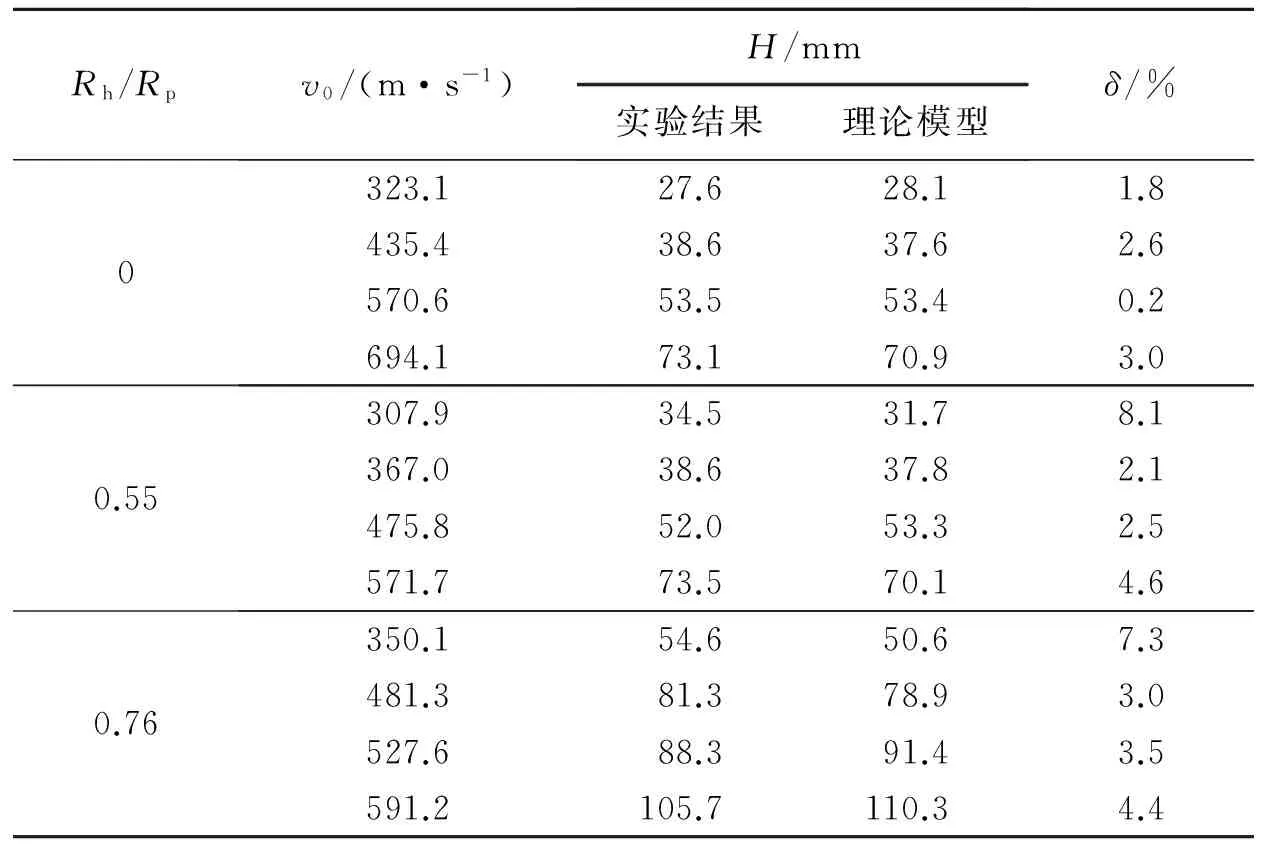
表1 侵彻深度实测值与计算结果的对比Table 1 Comparison of experimental results with theoretical calculation

3 卵形弹体侵彻预开孔靶体影响因素分析

串联战斗部前级侵彻作用过程复杂，射流开孔尺寸及孔形不定，后级弹体同预开孔靶接触产生的轴向阻力不同，侵彻深度也不同。此外，弹体头部形状及侵彻速度对后级随进的侵彻结果影响也很大。

以串联随进原型弹麦菲斯托(MephiSto)战斗部后级动能弹侵彻C40混凝土靶为例，在已验证的计算模型基础上，研究侵彻速度、相对孔径、弹头曲径比及混凝土预开孔孔形对实际串联随进钻地弹后级随进战斗部侵彻性能的影响。参照战斗部技术性能表[18]，确定模型相关参数。弹体质量m=350 kg，弹径d=240 mm，C40混凝土靶体密度ρt=2.4 g/cm3，无围压强度fc=40 MPa，根据文献[11,13]的研究结果，弹靶间动摩擦因数选用μ=0.05。

3.1 侵彻速度的影响

利用预开孔侵彻理论研究弹头曲径比为4的弹体以200～1 000 m/s的速度正侵彻Rh/Rp=0、0.3、0.5和0.7的预开孔混凝土靶。由图6可见，弹体侵彻深度随入射速度和预开孔孔径的增大而增加，速度低于400 m/s时，侵彻深度提高量较小；随着速度提高弹体侵彻深度显著增加，且在相对孔径Rh/Rp≥0.5时，侵深增幅变大，侵彻速度每增加100 m/s相应的侵彻速度提高量大于25%。这是由于侵彻速度较高时，弹体侵彻预开孔靶体过程中稳定侵彻阶段历程相对较长且弹靶接触面积小，侵彻阻力相对较小，导致最终的侵彻深度有明显增加。

3.2 弹靶相对孔径的影响

计算弹体以相同速度正侵彻不同相对孔径(Rh/Rp=0～0.8)柱形预开孔混凝土靶的侵彻结果。计算中弹体头部曲径比为4，速度分别为250、500和750 m/s。由计算结果(见图7)可以看出，相对孔径较小的情况，随相对孔径的增加，弹体以同一速度侵彻预开孔混凝土靶的侵彻深度增大较慢，当Rh/Rp≥0.4时，侵彻深度随相对孔径的增大明显加快，特别在Rh/Rp=0.6～0.8时，侵彻深度提高较快，相对孔径每增加0.1，相应的侵彻深度提高量超过16%。

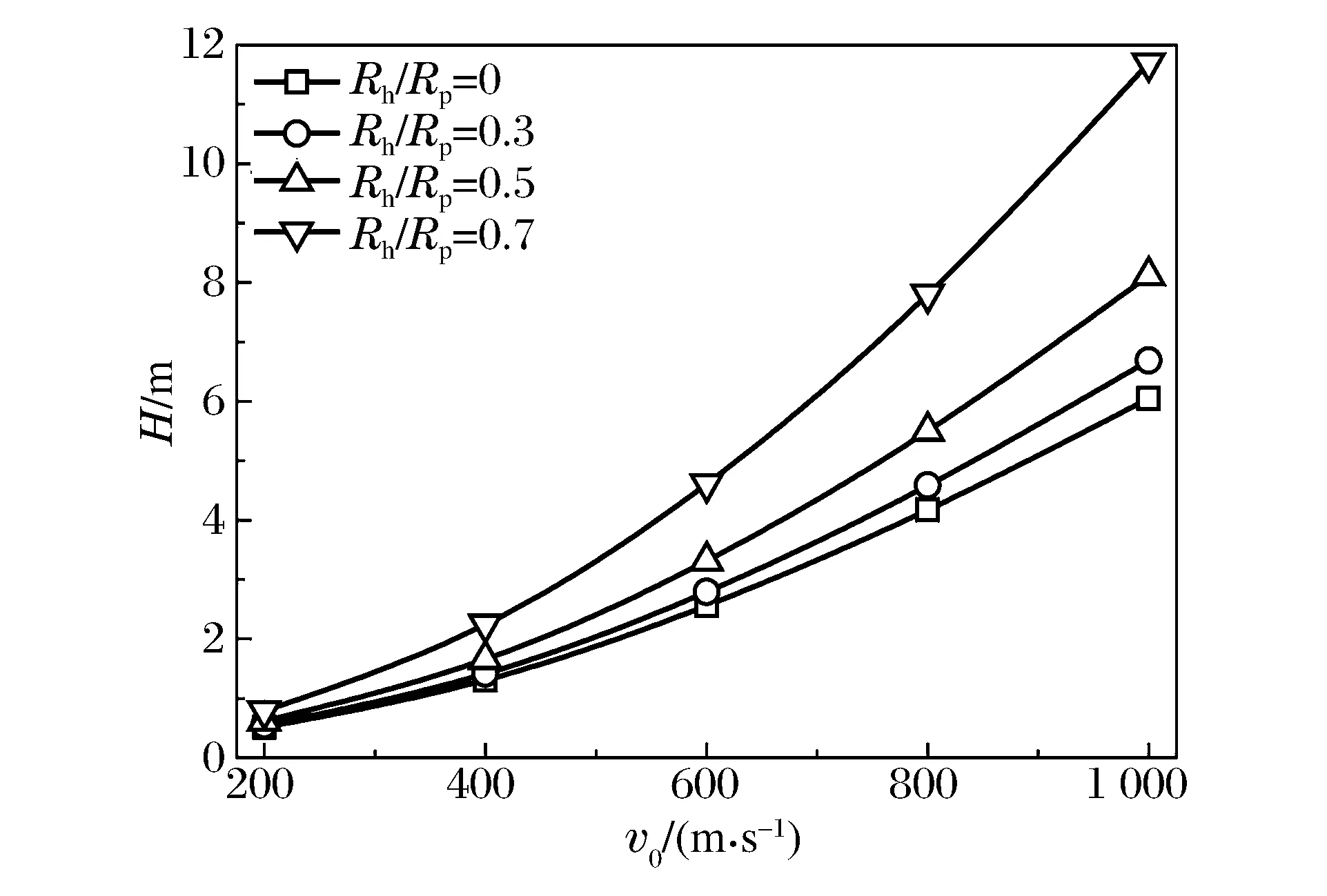
图6 靶体开孔情况下入射速度与侵彻深度的关系Fig.6 Velocity vs. penetration depth into pre-drilled targets

图7 靶体开孔情况下相对孔径与相对侵彻深度的关系Fig.7 Relative cavity radius vs. relative penetration depth into pre-drilled targets

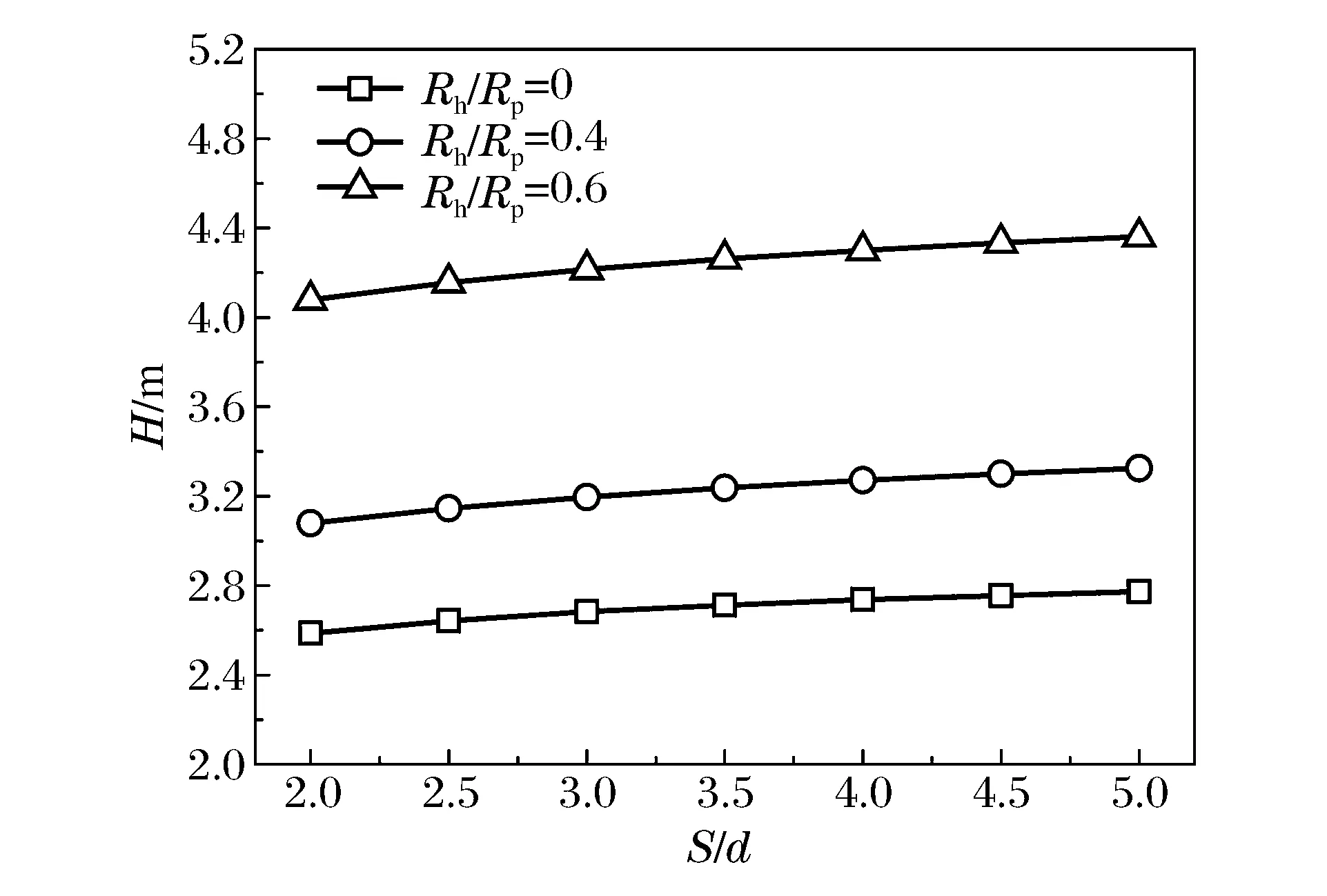
图8 不同开孔下的弹体头部曲径比与侵彻深度的关系Fig.8 CRH vs. penetration depthinto pre-drilled targets

3.3 弹体头部形状(曲径比)的影响

基于弹体质量相同的条件，分别计算不同弹头曲径比情况下，弹体以600 m/s速度侵彻3种相对孔径预开孔混凝土靶体，研究弹体头形对预开孔混凝土靶侵彻结果的影响规律。由图8可知，对于不同预开孔靶情况，随弹头曲径比的增大，侵彻深度单调增加，但提高不显著，曲径比为5对应的侵彻深度与曲径比为2的相比，提高量均低于10%。分析表明，串联随进侵彻过程中，改变卵形弹体头部形状(曲径比)能够影响其侵彻性能，相对侵彻速度及预开孔孔径，弹体头部形状(曲径比)对其影响较小。

3.4 预开孔参数的影响

串联战斗部侵彻作用过程中，在炸高、射流侵彻损耗、靶体材料特性等因素的影响下，聚能装药实际开孔孔形一般为近似锥形。基于肖强强等[19-20]的聚能射流侵彻混凝土开孔孔形研究，得到典型锥形开孔的锥角，并以孔深度和孔容积相等为标准，给出如表2所示的不同锥角下的靶体预开孔参数，表中h为孔深，Vc为孔容积，θ为半锥角，θ=0°为与锥形开孔等效的柱形开孔。

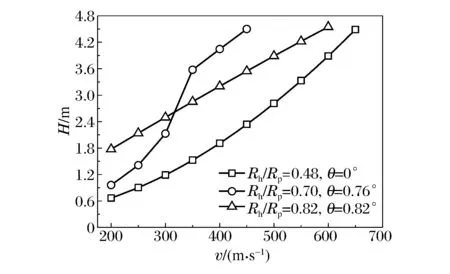
图9 锥形开孔靶体侵彻速度与侵彻深度的关系Fig.9 Velocity vs. penetration depth into concrete targets with various pre-drilled taper holes

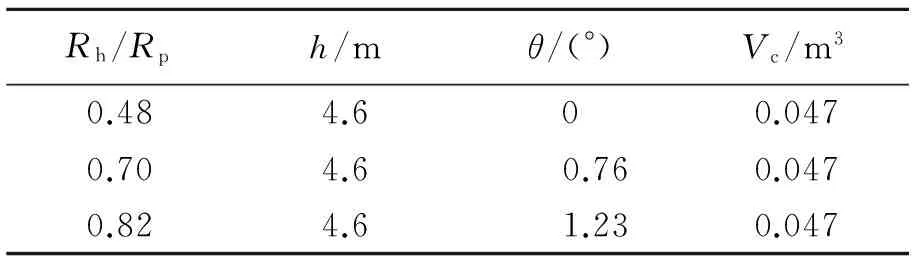
表2 靶体锥形预开孔参数Table 2 Taper hole parameters

基于理论模型及表2中的参数，计算不同锥形预开孔情况下弹体的侵彻深度。由图9可知，孔深和孔容积一定时，孔锥角及入口孔径直接影响弹体侵彻深度随速度变化规律。在θ=0°的特殊情况，侵彻深度随速度的提高呈指数形式增加。由于孔容积一定，对于有一定锥度的预开孔侵彻，侵彻深度变化趋势同锥角和孔径相关，在θ=1.23°、Rh/Rp=0.82情况下，侵彻深度近似呈线性变化。当预开孔参数为θ=0.76°、Rh/Rp=0.70，侵彻速度低于350 m/s时，侵彻深度随速度增加呈指数趋势急剧提高；而速度相对较高时，侵彻深度趋势明显减缓，但侵彻深度大于θ=1.23°、Rh/Rp=0.82时的侵深，这是由于较高速度下侵彻较大锥孔一定深度后，弹体仍具有较高的剩余速度，弹靶接触面积增大、阻力增加进而导致侵彻深度趋势变化。该现象说明预开孔侵彻过程弹体的受力状态受相对开孔孔径及锥角制约。以上分析表明，在弹体条件相同的情况下，串联战斗部前级近似锥形预开孔孔形对后级弹体侵彻性能影响较大。该结果可为串联战斗部设计中前后级匹配关系问题的确定提供一定的参考。

4 结 论

基于理想锥形开孔假设和库仑摩擦模型，发展完善了一种考虑扩孔/开坑阶段的预开孔侵彻模型，定义扩孔/开坑区域侵彻深度与弹径及预开孔径的关系，再结合空腔膨胀理论确定弹体阻力，进而得到最终的侵彻深度，该分析模型诠释了弹体侵彻全过程并能较好预测不同弹靶情况的侵彻深度，与实验结果吻合较好。

通过研究得到如下结论：(1)侵彻速度是卵形弹体侵彻预开孔混凝土靶性能的重要因素，速度大于400 m/s、孔径较大时，侵彻速度每增加100 m/s相应的侵彻深度提高量大于25%；(2)在弹体几何尺寸及速度一定时，预开柱孔孔径是影响侵彻性能的关键因素，侵彻深度与预开孔孔径呈正比，在Rh/Rp=0.6～0.8时，每增加0.1倍相对孔径侵彻深度提高量超过16%；(3)靶体预开孔孔锥角、相对孔径和弹体侵彻速度变化共同影响最终的侵彻结果，如何合理匹配串联战斗部后级弹体头部形状、侵彻速度与前级预开孔径，是提高战斗部侵彻效能的关键。

[1] Teland J A. Cavity expansion theory applied to penetration of targets with pre-drilled cavities[C]∥19th International Symposium on Ballistics. Interlaken, Switzerland: IBC, 2001:1329-1335.

[2] 张雷雷,黄风雷.基于修正空腔膨胀理论的随进弹丸侵彻规律分析[J].北京理工大学学报,2007,26(12):1038-1042. Zhang Leilei, Huang Fenglei. Analysis on the penetration performance of a following projectile based on modified cavity expansion theory[J]. Transactions of Beijing Institute of Technology, 2007,26(12):1038-1042.

[3] 王树有.串联侵彻战斗部对钢筋混凝土介质的侵彻机理[D].南京：南京理工大学,2006.

[4] 王静,王成.修正的卵形弹丸侵彻带有预制孔混凝土靶板的理论模型与数值模拟研究[J].计算力学学报,2009,26(4):558-561. Wang Jing, Wang Cheng. A modified theoretical model of the concrete target with pre-drilled cavities penetrated by the ogive-nose projectile and its numerical simulations[J]. Chinese Journal of Computational Mechanics, 2009,26(4):558-561.

[5] 文鹤鸣,郭晓钧.空穴膨胀模型及其在二级弹头系统中的应用[C]∥第十一届全国冲击动力学学术会议文集.咸阳:中国力学学会,2013.

[6] Folsom Jr E N. Projectile penetration into concrete with an inline hole[R]. Lawrence Livermore National Laboratory, UCRL-53786, 1987.

[7] Mostert F J. Penetration of steel penetrators into concrete targets with pre-drilled cavities of different diameters[C]∥Proceedings of the 18th International Symposium on Ballistics. San Antonio, Texas, USA: IBC, 1999:1042-1048.

[8] 冯兴民.空腔膨胀的数值模拟研究及其在侵彻力学中的应用[D].长沙：国防科学技术大学,2011.

[9] Forrestal M J, Altman B S, Cargile J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994,15(4):395-405.

[10] Forrestal M J, Warren T L. Penetration equations for ogive-nose rods into aluminum targets[J]. International Journal of Impact Engineering, 2008,35(8):727-730.

[11] 柴传国,皮爱国,武海军,等.卵形弹体侵彻混凝土开坑区侵彻阻力计算[J].爆炸与冲击,2014,34(5):630-635. Chai Chuanguo, Pi Aiguo, Wu Haijun, et al. A calculation of penetration resistance during cratering for ogive-nose projectile into concrete[J]. Explosion and Shock Waves, 2014,34(5):630-635.

[12] Forrestal M J, Frew D J, Hanchak S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[13] 吴昊,方秦,龚自明.考虑刚性弹弹头形状的混凝土 (岩石) 靶体侵彻深度半理论分析[J].爆炸与冲击,2012,32(6):573-580. Wu Hao, Fang Qin, Gong Ziming. Semi-theoretical analyses for penetration depth of rigid projectiles with different nose geometries into concrete (rock) targets[J]. Explosion and Shock Waves, 2012,32(6):573-580.

[14] Piekutowski A J, Forrestal M J, Poormon K L, et al. Penetration of 6061-T6511 aluminum targets by ogive-nose Steel projectiles with striking velocities between 0.5 and 3.0 km/s[J]. International Journal of Impact Engineering, 1999,23(1):723-734.

[15] Forrestal M J, Okajima K, Luk V K. Penetration of 6061-T651 aluminum targets with rigid long rods[J]. Journal of Applied Mechanics, 1988,55(4):755-760.

[16] Forrestal M J, Frew D J, Hanchak S J, et al. Penetration of grout and concrete targets with ogive-nose steel projectiles[J]. International Journal of Impact Engineering, 1996,18(5):465-476.

[17] Wang Y N, Wu H J, Huang F L, et al. Analysis of rigid motion for penetration of concrete[C]∥Proceedings of the 7th International Conference on Shock & Impact Loads on Structures. Beijing: The Chinese Society of Theoretical and Applied Mechanics, 2007:627-638.

[18] 午新民,王中华.国外机载武器战斗部手册[M].北京：兵器工业出版社,2005.

[19] 肖强强,黄正祥,祖旭东.双材质复合射流对混凝土的侵彻[J].爆炸与冲击,2014,34(4):457-463. Xiao Qiangqiang, Huang Zhengxiang, Zu Xudong. Penetration of jacketed jet into concrete[J]. Explosion and Shock Waves, 2012,32(6):573-580.

[20] 肖强强.聚能装药对典型土壤/混凝土复合介质目标的侵彻研究[D].南京：南京理工大学,2012.

(责任编辑 曾月蓉)

An analytic model of penetration for oval-nosed projectile penetrating into pre-drilled target

Deng Jiajie1，Zhang Xianfeng1，Qiao Zhijun1,2，Guo Lei1，He Yong1，Chen Dongdong1

(1.MinisterialKeyLaboratoryofZNDY，NanjingUniversityofScienceandTechnology,Nanjing210094，Jiangsu，China;2.TheUnit95856ofPLA，Nanjing210000，Jiangsu，China)

In this work, to investigate the penetration performance of a projectile into pre-drilled targets, we proposed and improved a penetration model of an oval-nosed projectile penetrating into the pre-drilled target using the conical pre-drilling assumption and coulomb friction model for analyzing the hole drilling/reaming versus the penetration depth and stabilization of the projectile. The analytic model was verified with tests of the projectile penetrating targets made from brittle and elastic-plastic targets. The results from our improved model are fairly consistent with those from the tests. In the case of a cylindrical hole, the impact velocity, CRH and the cavity/radius ratio are in direct proportion to the projectile's penetrating depth into a pre-drilled target. Withe same volume of the penetration, the angle of the conical hole and the relative has a great influence on the penetration depth, and the greater the angle, the weaker the degree to which CRH affects the penetration performance.

mechanics of explosion; penetration; cavity expansion theory; pre-drilled target; tandem warhead

10.11883/1001-1455(2016)05-0625-08

2015-02-04； < class="emphasis_bold">修回日期：2015-05-20

2015-05-20

国家自然科学基金项目(10902053)；中央组织部青年拔尖人才支持计划项目(2014年)； 爆炸冲击防灾减灾国家重点实验室(解放军理工大学)开放基金项目(DPMEIKF201405)

邓佳杰(1990— )，男，博士研究生,jiajie_0827@163.com。

O385 <国标学科代码：13035 class="emphasis_bold"> 国标学科代码：13035 文献标志码：A国标学科代码：13035

A