环形方管道中爆轰胞格的三维研究*
归明月,范宝春,张 辉
(1.南京理工大学瞬态物理重点实验室,江苏 南京 210094;2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
环形方管道中爆轰胞格的三维研究*
归明月1,2,范宝春1,张 辉1
(1.南京理工大学瞬态物理重点实验室,江苏 南京 210094;2.北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
通过实验和三维数值模拟研究了爆轰波在环形管道内的传播。实验采用烟迹板记录了爆轰波的胞格结构。数值模拟基于带化学反应的三维Euler方程,采用五阶精度的WENO格式捕捉激波,采用具有TVD性质的三阶Runge-Kutta法处理时间项,并结合并行技术,对爆轰波的传播进行了数值研究。结果表明,环形管道外壁为收敛壁面,由于其对流场的压缩效应,外壁面及附近的胞格较小,且较均匀。而内壁为发散壁面,其对流场起稀疏效应,内壁面及附近的胞格较大,且呈周期性变化。同时,不同壁面的胞格结构均出现了拍波(slapping wave),其形状呈弯曲的折线。
爆炸力学;自持传播;三维数值模拟;爆轰胞格;环形管道
在预混可燃介质中,由激波诱导的、以稳定方式传播的燃烧称为爆轰波。由于该燃烧的化学反应比较剧烈,因此具有极高的火焰传播速度,其产物也具有极高的温度和压力。这些特性使得爆轰具有两个重要的应用背景,一个是工业灾害的防治,另一个是航空航天领域的应用,如脉冲爆轰发动机、驻定爆轰发动机、旋转爆轰发动机等。因而,与爆轰相关的基础理论研究引起了广泛的关注。
大量的实验和数值研究表明,自持的爆轰波具有复杂的三维非定常结构,其波阵面三波点的轨迹形成了胞格结构,胞格的宽度体现了燃料的爆轰本征特性。最早关于爆轰波三维结构的实验研究可追朔到20世纪60年代的D.White等[1]和R.Strehlow[2]的研究。随后,J.Lee等[3]在方管中通过烟膜记录观察到了爆轰波的单头螺旋模式(spinning mode)。M.Hanana等[4]通过实验研究了直管中爆轰波的胞格结构,提出了2种爆轰波模式:矩形模式(rectangular mode)和对角模式(diagonal mode)。然而,由于实验测量手段的限制,爆轰波三维结构中瞬态流场的许多详细信息无法获得。因而,数值研究对实验研究起到了很好的补充。通过早期对爆轰波一维[5]和二维[6-7]的数值模拟,爆轰流场的稳定性和结构特性得到了较好的理解。随着计算机性能的提升和高精度算法的发展,爆轰波三维结构的数值研究[8-12]逐渐展开,并借助数值手段再现了爆轰波结构中的上述3种模式。以上的研究均是在直管中进行的。
但是,在实际应用中,爆轰波并不仅仅是在直管中传播,比如旋转爆轰发动机中,爆轰波是在环形管道中传播的。因此,对环形管道中爆轰波结构的研究对理解旋转爆轰发动机中爆轰波的稳定传播有重大的指导意义。张旭东等[13-14]对爆轰波在环形管道内的传播进行了实验和二维数值研究,结果表明,在外壁面过驱爆轰的带动下,内壁面依次经历爆轰熄火和再生的周期变化。王昌建等[15]对弯管内爆轰波的传播进行了实验和数值研究,结果表明,壁面稀疏波和压缩波的影响使爆轰波阵面发生畸变,但由于弯管曲率半径较大,未出现爆轰熄灭。H.Nakayama等[16]和Y.Sugiyama等[17]通过对弯曲管道内爆轰的传播进行实验和数值研究,来确定爆轰波稳定传播的条件。结果表明,弯曲管道内径的曲率半径越大,爆轰波越稳定。爆轰稳定传播的临界曲率半径是内径等于胞格宽度的21~32倍。然而,以上研究均是针对二维情形的,无法体现爆轰波结构的三维本质。
本文中通过实验和三维数值模拟对爆轰波在环形管道中的传播进行研究。实验采用烟膜技术,得到环形管内爆轰波传播的胞格图。数值计算采用五阶精度的WENO格式,结合并行技术,得到稳定传播的爆轰波,分析相应的胞格结构。
1 实验系统
实验装置如图1所示,由爆轰管、环形管道和泄爆管组成。爆轰管的横截面为30 mm×10 mm,长度为2 000 mm,其作用是产生稳定的爆轰波。环形管道与爆轰管之间用法兰连接,其横截面尺寸与爆轰管一样,内径为85 mm,外径为115 mm,其作用是做为测试段研究旋转爆轰传播特性。泄爆管一端与环形管道相连,另一开口端用薄膜密封,其横截面尺寸与爆轰管、环形管道一样,其作用是防止外面空气回流对胞格图像的破坏。
实验时,向已经抽成真空的实验装置充入等当量比的预混可燃气体。利用爆轰管底端的等离子体点火,迅速形成爆轰。随后,爆轰波进入环形管道,在预先放置于环形管道底部的烟迹板上形成胞格结构。最后,爆轰波从泄爆管泄出,进入管外的大气。实验气体为等当量比的氢气/空气预混气体,初始压力和温度分别为10 kPa和300 K。

图1 实验装置图Fig.1 Experimental setup
2 数值模拟
假设混合气体为理想气体,忽略扩散、黏性和热传导,在贴体坐标系中,带化学反应的三维Euler方程为:
(1)
式中:守恒向量Q,对流通量F、G、H及源项S的表达式分别为:
(2)
式中:u、v、w分别是笛卡尔坐标系中x、y、z方向的速度分量,且
(3)
t、ρ、p和Z分别表示时间、混合物的密度、压力和反应物的质量分数。e为单位质量总能量,e满足以下关系式:
e=p/[ρ(γ-1)]+(u2+v2+w2)/2+Zq
(4)
式中:q为反应热。化学反应采用单步不可逆反应,反应速率满足
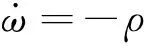
(5)
式中:Af为指前因子,Ea为活化能,R为通用气体常数。本文中所用预混气为氢气/空气混合物,方程中的热力学和化学动力学参数采用文献[18]采用的参数,量纲一参考状态取p0=100 kPa,T0=300 K。
数值计算时,采用时间分裂格式,对流项采用五阶精度的WENO格式[19],时间项采用三阶TVD性质的Runge-Kutta法,同时结合了基于MPI的并行计算技术。
环形管道计算示意图如图2所示,其内外径分别为85、115 mm,高度为10 mm。为节省计算资源,本文中采用移动计算窗口(见图2(a)中阴影区域),使该窗口随着爆轰波一起运动,从而保证其始终覆盖着爆轰波。计算窗口所用网格数为ξ×η×ζ=300×800×100。

图2 环形管道计算示意图Fig.2 Schematic of computational domain in an annular tube

图3 爆轰波ZND结构中的化学反应度分布图Fig.3 Reaction progress distribution in ZND detonation structure
本文中计算所用氢气/空气混合物的初始条件为:压力p=10 kPa,温度T=300 K,在该条件下的ZND模型如图3所示,其中横坐标表示距离激波的长度,纵坐标表示化学反应度(λ=1-Z),图中可以观测到,半个反应区长度约为2.03 mm,本文中外壁面网格尺寸为0.1 mm,内壁面网格为0.074 mm,意味着半个反应区至少有20个网格,这样的网格尺寸足以描述爆轰波的精细结构。计算时,以一维ZND结构的分析解作为初始条件,赋值于图2(b)中阴影区域(位置η=0处),环形管道其余区域的状态为:压力p=10 kPa,温度T=300 K。
在移动计算窗口,顶部和底部均为滑移、绝热固壁边界条件,前后部均为零梯度条件,内外壁面采用的边界条件为:
3 结果与讨论

图4 环形管道顶部的爆轰胞格结构Fig.4 Cellular structure of detonation on top wall of annular tube
图4为环形管道顶部的爆轰波的胞格结构。由图可见,实验和数值计算结果定性一致,均反映了爆轰波可以稳定旋转,且外侧胞格明显小于内侧胞格。在爆轰波的精细结构中,沿着波阵面横向传播的横波是支持爆轰波稳定传播和形成胞格结构的关键,而横波的间距直接影响胞格的宽度和爆轰波的强度。环形管道内外壁面具有收敛和发散的特性,该特性使其附近的流场发生相应的变化,进而改变胞格的尺寸。外壁面为凹型收敛壁面,对流场有压缩作用,压力得不到足够的疏解,因而形成过驱爆轰,爆轰胞格变小;而内壁面为凸型发散壁面,其膨胀效应使爆轰波削弱,爆轰胞格变大。同时,这种敛散作用使爆轰波阵面各处的线速度不同,即外壁面的线速度最大(约1 728.5 m/s),内壁面的线速度最小(约1 252.5 m/s),从而使爆轰波以稳定的角速度(约1.68°/s)旋转,即使旋转爆轰波自持。

图5 环形管道内爆轰波的三维胞格结构Fig.5 3D cellular structure of detonationin annular tube

图6 环形管道内的爆轰胞格结构(爆轰波从左往右传播)Fig.6 Cellular structure of detonation in an annular tube (detonation propagation from left to right)
爆轰波本质是三维结构,其在环形管道内传播时的三维胞格结构如图5所示,内外壁的敛散性使得环形管道不同壁面的胞格具有不同的特性,图5还描述了爆轰胞格的生成、发展和稳定传播过程。为了详细分析该过程,将管道内外壁面展开,如图6所示,图6(a)、(b)分别表示环形管道位置角η=0~π/2、π/2~π时的胞格结构。初始时刻,将ZND结构爆轰赋值于环形管道的底端(方位角为0°),随后,上下壁面的反射和内外壁面的敛散的联合作用使爆轰波阵面弯曲,出现不规则反射,形成横波,胞格结构开始出现,通过流场的自调整,大约在π/3附近时,形成的胞格开始稳定,如图6(a)所示。外壁面的强烈压缩使得外壁面的胞格和顶部壁面中靠近外侧的胞格均比较小,且胞格的宽度一直维持在2.5 mm左右。而内壁面的发散效应使得内壁面的胞格呈现周期性的变化,其胞格宽度在10~20 mm之间变化,如图6(b)所示。同时,沿着径向,胞格的大小从内壁到外壁逐渐减小。同时,在3个壁面的胞格图像中,均可以观察到拍波(slapping wave),即胞格结构中沿着横波方向的亮光区域,其呈现弯曲的折线状,这与直管中观察到的拍波形状[4]是不一样的,这是由于内外壁面的敛散性改变了爆轰波结构的流场特性所致,而拍波只有在三维结构中才可以被观察到。
4 结 论
通过实验和三维数值模拟研究了爆轰波在环形管道中传播的胞格结构,结果表明,环形管道外壁为凹型收敛壁面,内壁为凸型发散壁面,该几何特性使流场被压缩或稀疏,从而导致外壁及其附近的胞格较小,且较均匀,而内壁及其附近的胞格较大,且呈周期性变化。同时,爆轰波阵面的线速度从内侧到外侧逐渐增加,从而维持爆轰波以稳定的角速度自持旋转。在环形管道的不同壁面观察到了拍波结构,其呈弯曲的折线状。
[1] White D, Cary K. Structure of gaseous detonation. II. Generation of laminar detonation[J]. Physics of Fluids, 1963,6(5):749-750.
[2] Strehlow R. Multi-dimensional detonation wave structure[J]. Astronaut Acta, 1970,15(5):345-357.
[3] Lee J H, Oppenheim A K. Current views on gaseous detonation[J]. Astronaut Acta, 1969,14(5):565-584.
[4] Hanana M, Lefebvre M, Tiggelen P. Pressure profiles in detonation cells with rectangular and diagonal structures[J]. Shock Waves, 2001,11(2):77-88.
[5] Bourlioux A, Majda A, Roytburd V. Theoretical and numerical structure for unstable one-dimensional detonations[J]. SIAM Journal on Applied Mathematics, 1992,90(3/4):211-229.
[6] Bourlioux A, Majda A. Theoretical and numerical structure for unstable two-dimensional detonations[J]. Combustion and Flame, 1991,51(2):303-343.
[7] Gamezo M, Desbordes D, Oran E. Formation and evolution of two-dimensional cellular detonations[J]. Combustion and Flame, 1999,116(1/2):154-165.
[8] Williams D, Bauwens L, Oran E. Details structure and propagation of three-dimensional detonations[J]. Proceedings of the Combustion Institute, 1996,26:2991-2998.
[9] Deledicque V, Papalexandris M. Computational study of three-dimensional gaseous detonation structures[J]. Combustion and Flame, 2006,144(4):821-837.
[10] Dou H, Tsai H, Khoo B, et al. Simulations of detonation wave propagation in rectangular ducts using a three-dimensional WENO scheme[J]. Combustion and Flame, 2008,154(4):644-659.
[11] Wang C, Shu C, Han W, et al. High resolution WENO simulation of 3D detonation waves[J]. Combustion and Flame, 2013,160(2):447-462.
[12] Huang Y, Ji H, Lien F, et al. Numerical study of three-dimensional detonation structure transformation in a narrow square tube: From rectangular and diagonal modes into spinning models[J]. Shock Waves, 2014,24(4):375-392.
[13] 张旭东,范宝春,潘振华,等.旋转爆轰胞格结构的实验及数值研究[J].爆炸与冲击,2011,31(4):337-342. Zhang Xudong, Fan Baochun, Pan Zhenhua, et al. Experimental and numerical investigation on cellular patterns of rotating detonations[J]. Explosion and Shock Waves, 2011,31(4):337-342.
[14] Zhang X D, Fan B C, Pan Z H, et al. Experimental and numerical study on detonation propagating in an annular cylinder[J]. Combustion Science and Technology, 2012,184(10/11):1708-1717.
[15] 王昌建,徐胜利,费立森.等.弯管内爆轰波传播的流场显示和数值模拟[J].力学学报,2006,38(1):9-15. Wang Changjian, Xu Shengli, Fei Lisen, et al. Schlieren visualization and numerical simulation on gaseous detonation propagation through a bend tube[J]. Journal of Theoretical and Applied Mechanics, 2006,38(1):9-15.
[16] Nakayama H, Moriya T, Kasahara J, et al. Stable detonation wave propagation in rectangular-cross-section curved channels[J]. Combustion and Flame, 2012,159(2):859-869.
[17] Sugiyama Y, Nakayama Y, Matsuo A, et al. Numerical investigations on detonation propagation in a two-dimensional curved channel[J]. Combustion Science and Technology, 2014,186(10/11):1662-1679.
[18] Gamezo V, Ogawa T, Oran E. Flame acceleration and DDT in channels with obstacles: Effect of obstacle spacing[J]. Combustion and Flame, 2008,155(1/2):302-315.
[19] Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996,126(2):202-228.
(责任编辑 曾月蓉)
Three-dimensional study of detonation cell in annular tube
Gui Mingyue1,2, Fan Baochun1, Zhang Hui1
(1.LaboratoryofTransientPhysics,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China;2.StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China)
In this work we carried out experimental and 3D numerical study of cellular structure of detonation propagating in an annular tube. Detonation cellular patterns were recorded using a smoked foil. Based on the 3D reactive Euler equations with the one-step irreversible Arrhenius kinetics model, detonation propagation of hydrogen/air mixture in an annular tube was investigated numerically. Fifth-order weighted essentially non-oscillatory (WENO) scheme and third-order TVD Runge-Kutta were used to discretize the spatial derivatives and the time term, respectively. Moreover, parallel technology was also adopted. The results indicate that the outer wall of the annular tube is the convergent wall, which reduces the cell sizes of the outer wall and makes it more uniform due to its compression. However, the inner wall of the annular tube is the divergent wall, which enlarges the cell sizes of the inner wall and leads to its periodical variation due to its expansion. Simultaneously, slapping waves appear in all the tube walls and its shape is a bent line.
mechanics of explosion; self-sustained propagation; three-dimensional simulation; detonation cell; annular tube
10.11883/1001-1455(2016)05-0577-06
2015-03-24; < class="emphasis_bold">修回日期:2015-09-07
2015-09-07
国家自然科学基金项目(11202104); 爆炸科学与技术国家重点实验室(北京理工大学)开放基金项目(KFJJ13-3M)
归明月(1977— ),男,博士,副研究员,mygui@njust.edu.cn。
O382 <国标学科代码:13035 class="emphasis_bold"> 国标学科代码:13035 文献标志码:A国标学科代码:13035
A

