全加器在逻辑设计中的应用

唐民丽，吴恒玉

(海南软件职业技术学院 电子工程系，海南 琼海　571400)



全加器在逻辑设计中的应用

唐民丽，吴恒玉

(海南软件职业技术学院 电子工程系，海南 琼海571400)

摘要：从全加器的逻辑功能和通用性出发，提出一些应用全加器的非常规逻辑电路设计方法，并举例说明全加器的逻辑设计过程及全加器在逻辑电路设计中的具体应用方法.利用全加器的非常规逻辑电路设计方法，具有使用方便、设计迅速、简化电路等优点.

关键词：全加器；逻辑设计；应用

全加器的基本功能是实现二进制数的算术加运算，表1所示是一位全加器的真值表，图1所示是其逻辑符号，其中：A为被加数；B为加数；C为低一位来的进位数；S为本位和；J为向高一位的进位数[1-2].

两个输出函数的逻辑表达式为

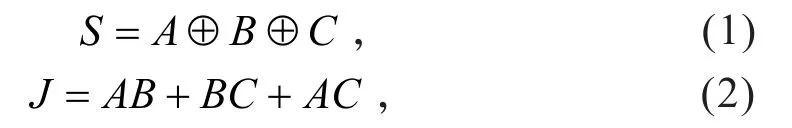
表1　全加器真值表

图1　全加器逻辑符号

式(1)、(2)表明，全加器还具有逻辑运算功能.

全加器在组合逻辑电路设计中的应用有：用全加器构成逻辑门，用全加器构成奇、偶判别电路，用全加器构成多数判别电路.

1　用全加器构成逻辑门

令式(1)、(2)中的一个或两个输入变量为常量，则可用全加器构成逻辑门.

1) 令C=0或接地时，S= A⊕ B，J=AB，此时全加器可作为异或门及与门使用.

2) 令C=0，B=0或C=1，B=1时，S=A，此时全加器可作为传输门使用.

4) 令C=1时，S= Ae B，J=A+B，此时全加器可作为同或门和或门使用.

2　用全加器构成奇、偶判别电路

当输入变量的取值含有奇数个1时，输出为1，为奇数判别；当输入变量的取值含有偶数个1时，输出为1，为偶数判别[1-2].

表1及式(1)表明，全加器的和数输出即为三变量奇、偶判别函数.将多个全加器级联，可实现多于三个输入变量的奇、偶判别电路[1-2].

表2　四个输入变量的奇、偶判别电路真值表

例如，表2是四个输入变量A、B 、C、D的奇、偶判别电路的真值表，F1为奇数判别输出，F2为偶数判别输出.由表2可写出F1的表达式为

用二级全加器实现时，将式(3)改写成

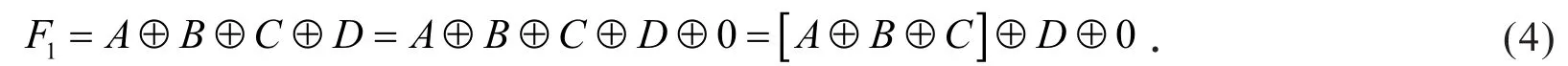
按式(4)可画出逻辑电路图如图2所示.

由表2可写出F2的表达式为

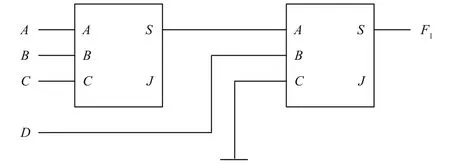
图2　四个输入变量的奇数判别电路

用二级全加器实现时，将式(5)改写成

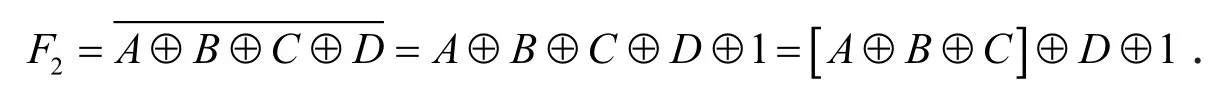
按式(5)可画出逻辑电路图如图3所示.

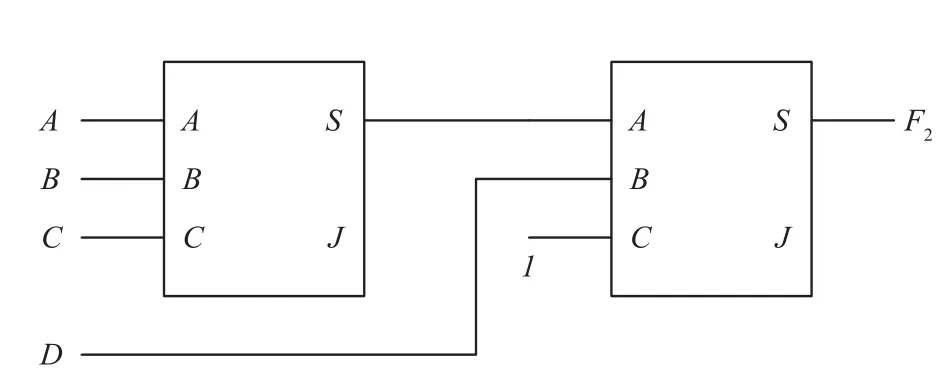
图3　四个输入变量的偶数判别电路

按此方法可以用全加器构成更多输入变量的奇、偶判别电路.

3　用全加器构成多数判别电路

多数判别的功能是：当输入变量取值为1的占多数时，输出为1，显然要求输入变量个数为奇数.表1及式(2)表明，全加器的进位输出J即为三变量的多数判别函数.

为便于推广到多于三个变量的多数判别情况，将表1改变成表3的形式，即将全加器的输出记为二进制数的形式，其中b2对应原表中的J，b1对应原表中的S，判别结果F在b2、b1上产生.以b2、b1为变量作F的卡诺图[3]，如图4所示，得F=b2，即为全加器的进位输出J.

当输入变量多于三个且为奇数时，可将所有变量求和得二进制数表示的和数，再以二进制和数为变量求输出F的表达式.用全加器实现二进制数的和数，用附加门实现函数F.表4为五个变量A、B、C、D、E多数判别的真值表，其中b4、b2、b1为二进制和数，F为判别输出函数.

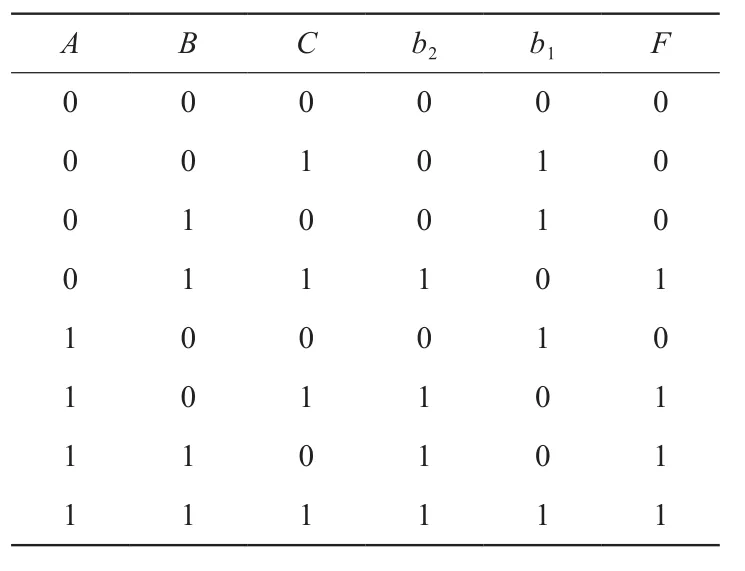
表3　修改后的三个变量多数判别真值表

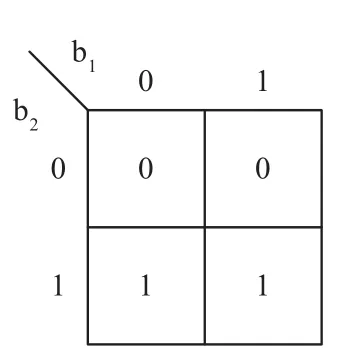
图4　F的卡诺图

表4　五个变量多数判别的真值表

以b4、b2、b1为变量作的卡诺图如图5所示[3-5]，可得 F=b4+b2b1.

用三个全加器实现A、B、C、D、E求和，得二进制和数，用与门、或门实现，画出逻辑电路图如图6所示.

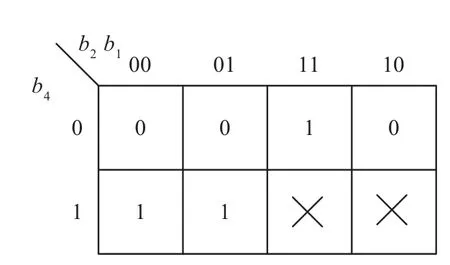
图5　F的卡诺图

图6　五变量的多数判别电路

4　结论

利用全加器的非常规逻辑电路设计方法，不仅使逻辑电路的设计更加简单，而且可以充分发挥全加器的应用潜力，所以此设计方法在逻辑电路的设计中应用，不仅具有使用方便、设计迅速、简化电路等优点，而具有一定的实用意义.

参考文献：

[1]李中发.数字电子技术[M].北京：中国水利水电出版社，2008：76-78.

[2]刘守义，钟苏.数字电子技术[M].西安：西安电子科技大学出版社，2001：2.

[3]吴恒玉，唐民丽.函数子卡诺图及其在逻辑设计中的应用[J].华北科技学院学报，2005，2(2)：84-85.

[4]吴恒玉，唐民丽.次态卡诺图在时序逻辑电路中的应用[J].南京工业职业技术学院学报，2006(2)：71-73.

[5]吴恒玉.引入变量卡诺图(VEM)的作图方法[J].河北北方学院学报，2007(1)：1-3.

(责任编辑：沈凤英)

The Application of Full Adder in the Logical Design

TANG Min-li，WU Heng-yu
(Department of Electronic Engineering，Hainan College of Software Technology，Qionghai 571400，China)

Abstract：This paper provides some design methods of irregular logical circuits with full adders based on the logical function and universality of full adders.Some examples are given to illustrate the process of the logical design of full adders and the application methods in logical circuits designs in detail.This method enjoys such merits as convenience in usage， rapidity in design and simplification of the circuits.

Key words：full adder；the logical design；application

作者简介：唐民丽(1967-)，女，辽宁阜新人，教授，硕士，主要从事电子技术研究.

收稿日期：2015-12-03；修回日期：2015-12-30

DOI：10.16219/j.cnki.szxbzk.2016.01.004

中图分类号：TN79+1

文献标志码：A

文章编号：1008-5475(2016)01-0020-03

引文格式：唐民丽，吴恒玉.全加器在逻辑设计中的应用[J].苏州市职业大学学报，2016，27(1)：20-22.