特殊情况下的压力系数和自喷系数计算方法

李传亮，朱苏阳

（西南石油大学石油与天然气工程学院，成都610599）



特殊情况下的压力系数和自喷系数计算方法

李传亮，朱苏阳

（西南石油大学石油与天然气工程学院，成都610599）

摘要：压力系数是油气藏评价的基本参数，可以用来评价油气藏的压力状态。但是，在地形起伏较大的地区或高油气柱油气藏，用传统方法计算的压力系数会出现较大偏差。研究了压力系数计算出现偏差的原因，对于地形起伏较大的地区，主要是静水压力的计算出了偏差，把计算起始深度由地面改为潜水面，即可消除计算偏差。对于高油气柱油气藏，选取油气柱中部深度计算压力系数，即可消除计算偏差。油气藏压力—深度关系曲线的截距值，即油气藏流体流到地面的剩余压力，定义为油气藏流体的自喷系数，自喷系数越大，油气藏流体的自喷能力就越强。

关键词：油气藏；地层压力；静水压力；压力系数；异常高压；自喷系数

油气藏的压力状态可用绝对压力和相对压力（压力系数）2个指标进行评价。按地层压力（绝对压力）可以将油气藏分为低压油气藏（地层压力低于20 MPa）、中等压力油气藏（地层压力20～40 MPa）、高压油气藏（地层压力40～60 MPa）和超高压油气藏（地层压力大于60 MPa）[1]。压力系数定义为实测地层压力与相同深度处静水压力的比值[2]。按压力系数可以将油气藏分为异常低压油气藏（压力系数小于0.8）、正常压力油气藏（压力系数0.8～1.2）和异常高压油气藏（压力系数大于1.2）[3]。地层流体的自喷能力与绝对压力没有直接关系，而与相对压力有一定的关系，即压力系数越高，地层流体的自喷能力就越强。在过去相当长的时间内，压力系数的使用一直未出现问题[4-8]。但是，随着山区和塬上油气资源的开发，压力系数出现了令人匪夷所思的现象，一个油气藏的压力系数变化范围很大，即可以是异常高压，同时又可以是正常压力，有时候甚至还可以是异常低压，让开发管理人员无所适从。因此，需要对这一问题进行深入的研究。

1　压力系数

静水压力的计算公式为[1]

计算静水压力时，地层水的密度取1.0 g/cm3.静水压力随深度的变化趋势为一条直线（图1a）。

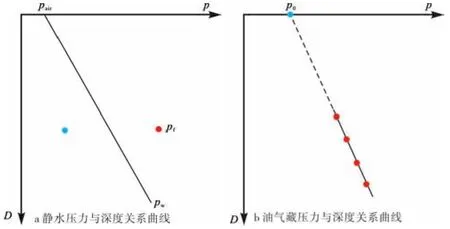
图1　静水压力和油气藏压力与深度关系曲线

实测地层压力偏离静水压力的程度用压力系数来衡量，计算公式为[3]

压力系数为相对压力，数值越高，说明地层流体的能量越强，其自喷能力也就越强。

2　自喷系数

把油气藏每一点的实测地层压力绘制在直角坐标系中，将得到一条直线（图1b），回归后得油气藏的压力与深度关系方程为

Gp为曲线的斜率，为油气藏流体密度与重力加速度的乘积。

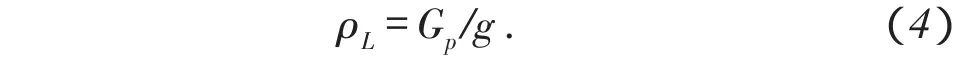
可以通过（4）式确定油气藏的流体密度，然后判断油气藏的流体类型[1]。若ρL>1.0 g/cm3，则为水；若ρL为0.5～1.0 g/cm3，则为油；若ρL<0.5 g/cm3，则为气。

（3）式中的p0为压力—深度关系曲线的外推截距，即D=0时的地层压力，也即流体从地下流到地面的剩余压力[1]。若p0低于或等于大气压，油气藏流体则不能自喷；若p0高于大气压，则能够自喷，而且数值越大，自喷能力就越强。笔者将油气藏的剩余压力p0定义为油气藏流体的自喷系数。p0<5 MPa时，油气井的自喷能力弱；p0为5～15 MPa时，自喷能力中等；p0> 15 MPa时，自喷能力强。

压力系数只能定性反映油气藏的能量，有些异常低压油气藏不能自喷，而有些却能够自喷。自喷系数则能定量反映油气藏的能量，不会出现模棱两可的情况，因而对生产实践具有直接的指导意义。

3　地形起伏大的情况

压力系数的计算公式是针对平坦地形而言的，静水压力的计算起点是地表，即产生静水压力的水柱高度与地层埋深相同。但是，当把（2）式用于起伏较大的地形时就会出现偏差，起伏较大的地形有2种：一是像鄂尔多斯盆地的塬上地区；二是像四川盆地的山区。

在塬上地区大部分油气井位于塬上的平台区，少部分油气井位于塬上的侵蚀沟里（图2）。

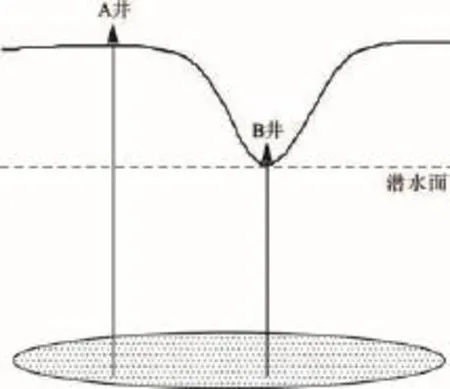
图2　塬上地形及油气井位置示意

若图2中油气藏的地层压力为7.00 MPa，B井的地层埋深为0.7 km，由（1）式计算的静水压力为6.96 MPa，由（2）式计算的压力系数为1.01，为正常压力油气藏；若A井的地层埋深为1.0 km，由（1）式计算的静水压力为9.90 MPa，由（2）式计算的压力系数为0.707，为异常低压油气藏。

A井和B井位于同一个油气藏，两井的压力状态却截然不同。

若图2中油气藏的海拔为-0.5 km，油气藏的流体密度为0.4 g/cm3，则油气藏压力与海拔的关系方程为

图2中A井的地面海拔为0.5 km，B井的地面海拔为0.2 km，代入（5）式计算得A井和B井的自喷系数分别为3.08 MPa和4.26 MPa.两口井的自喷能力很接近，皆为弱自喷能力。而由压力系数的计算结果可以看出，A井为异常低压，B井为正常压力，差别甚大。可见，在地形起伏较大情况下压力系数的计算出了偏差。之所以出现这种情况，是因为静水压力的计算不正确。

用（1）式计算静水压力时是从地面起算的，实际上静水压力应该从潜水面起算，因为静水压力是由地下静水柱产生的。由于实际的潜水面很难确定，为了计算方便，选取区域最低点作为潜水面的基准面，其他井都参考该基准面进行计算。因此，可将（1）式改写为

图2中A井的潜水面深度为0.3 km，B井的潜水面深度为0 km.将潜水面深度代入（6）式，计算A井和B井的静水压力均为6.96 MPa，代入（2）式计算的压力系数均为1.01，为正常压力油气藏。

对于四川盆地的山区，大部分油气井位于山下平地，少部分油气井位于山上（图3）。在计算压力系数和自喷系数时，采用与塬上相同的方法即可。

图3　山区地形及油气井位置示意

4　高油气柱的情况

即使在平原地区，若地层的油气柱较大，计算压力系数时也会出现偏差。图4中E井地层埋深为1.0 km，静水压力为9.90 MPa；F井地层埋深为0.7 km，静水压力为6.96 MPa.

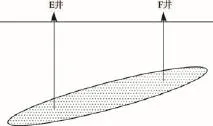
图4　高油气柱地层

若E井的实测地层压力为10.00 MPa，则压力系数为1.01，为正常压力。

若地层流体的密度为0.4 g/cm3，可以得出油气藏的压力—深度关系方程为

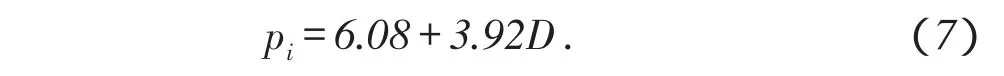
由于地势平坦，为了方便起见，（7）式采用了深度，而非海拔。由（7）式计算的F井的地层压力为8.82 MPa，压力系数为1.27，为异常高压。

同一个地层，也出现了两种截然不同的压力状态。由（7）式计算的E井和F井的自喷系数相同，皆为6.08 MPa，两口井的自喷能力均为中等。但是，两井的压力系数相差较大。之所以出现这种情况，是因为油气藏的油气柱较高所致，E井位于油气柱的底部，而F井位于油气柱的顶部，两口井的井底出现了较大的高差。

为了避免出现因为高差带来的压力系数计算偏差，在高油气柱的情况下，压力系数的计算选点应定在油气柱的中部，只有这样才能代表油气藏的平均压力状态。由E井和F井计算的油气藏中部深度为0.85 km，代入（1）式得静水压力为8.43 MPa.由（7）式计算出该深度处的地层压力为9.41 MPa，代入（2）式，得该油气藏的压力系数为1.12，为正常压力。

5　结论

（1）静水压力是地下静水柱产生的压力，计算静水压力时应从潜水面起算，而不应简单地从地面起算。

（2）对于存在地形起伏的山区和塬上来说，若从地面计算静水压力，将会导致压力系数的计算结果出现偏差，进而导致油气藏压力状态的误判。

（3）对于油气柱较高的油气藏，应该选取油气柱中部深度计算压力系数，否则将会出现偏差。

（4）油气藏压力—深度关系方程的截距压力（剩余压力）定义为油气藏的自喷系数，该数值越大，油气藏流体的自喷能力就越强。

符号注释

D——油气藏埋藏深度，km；

Dw——潜水面深度，km；

Gp——油气藏压力梯度，MPa/km；

g——重力加速度，m/s2；

H——海拔，km；

p0——油气藏剩余压力，自喷系数，MPa；

pair——大气压，MPa；

pf——实测地层压力，MPa；

pi——油气藏原始地层压力，MPa；

pw——静水压力，MPa；

α——压力系数，无因次；

ρL——油气藏流体密度，g/cm3；

ρw——地层水密度，g/cm3.

参考文献：

［1］李传亮.油气藏工程原理（第二版）［M］.北京：石油工业出版社，2011：107-120. LI Chuanliang.Fundamentals of reservoir engineering（2nd edition）［M］.Beijing：Petroleum Industry Press，2011：107-120.

［2］秦同洛，李璗，陈元千.实用油藏工程方法［M］.北京：石油工业出版社，1989：69-70. QIN Tongluo，LI Dang，CHEN Yuanqian.Practical reservoir engi⁃neering methods［M］.Beijing：Petroleum Industry Press，1989：69-70.

［3］SY/T6365—1998.油气藏原始地层压力及压力系统确定方法［S］.北京：石油工业出版社，1998. SY/T6365—1998.Methodology for the initial pressure and the hy⁃drodynamic system in hydrocarbon reservoirs［S］.Beijing：Petro⁃leum Industry Press，1998.

［4］薛国刚，高渐珍.东濮凹陷异常高压油气藏形成机理［J］.新疆石油地质，2014，35（2）：149-152. XUE Guogang，GAO Jianzhen.The formation mechanism of abnor⁃mal high pressure reservoirs in Dongpu sag,Bohai Bay basin［J］. XinjiangPetroleum Geology，2014，35（2）：149-152.

［5］唐守宝，高峰，樊洪海，等.库车坳陷大北地区白垩系—古近系异常高压形成机制［J］.新疆石油地质，2011，32（4）：370-372. TANG Shoubao，GAO Feng，FAN Honghai，et al.Formation mecha⁃nism of Cretaceous-Paleogene abnormal pressure in Dabei area of Kuqa depression,Tarim basin［J］.Xinjiang Petroleum Geology，2011，32（4）：370-372.

［6］李传亮.压力系数的上限值研究［J］.新疆石油地质，2009，30 （4）：490-492. LI Chuanliang.A study on the maximum of pressure factor of forma⁃tion［J］.XinjiangPetroleum Geology，2009，30（4）：490-492.

［7］李传亮.地层异常压力原因分析［J］.新疆石油地质，2004，25 （4）：443-445. LI Chuanliang.Analysis of abnormal reservoir pressure［J］.Xinji⁃angPetroleum Geology，2004，25（4）：443-445.

［8］王震亮，孙明亮，耿鹏，等.准南地区异常地层压力发育特征及形成机理［J］.石油勘探与开发，2003，32（1）：32-34. WANG Zhenliang，SUN Mingliang，GENG Peng，et al.The develop⁃ment features and formation mechanisms of abnormal high formation pressure in southern Junggar region［J］.Petroleum Exploration and Development，2003，32（1）：32-34.

（编辑叶良）

Calculation of Pressure Factor and Spontaneous Production Factor under Special Conditions

LI Chuanliang,ZHU Suyang
(School of Petroleum Engineering，Southwest Petroleum University，Chengdu,Sichuan 610599,China)

Abstract:Pressure factor is a basic parameter for petroleum reservoir evaluation,which can be used to analyze the pressure status of reser⁃voirs.However,in an area or reservoir with uneven surface and/or high hydrocarbon column,the calculation of pressure factor may lead to result with large deviations.This paper studies the reasons for the phenomena above.For the area with uneven surface,it is the calculation of hydrostatic pressure that leads to the deviations,which can be eliminated by replacing the depth from surface with depth from water lev⁃el.For the reservoir with high hydrocarbon column,it is the mischoice of calculation datum depth of pressure factor that results in deviated pressure factors,which can be eliminated by using the middle depth rather than the top or bottom depth of hydrocarbon column.The inter⁃cept pressure of hydrostatic pressure-depth curve,a surplus pressure of reservoir fluids flowing from underground to surface,is defined as spontaneous production factor of reservoir fluids.The larger the spontaneous production factor,the stronger the ability of reservoir fluids to flow spontaneously.

Keywords:reservoir；formation pressure；hydrostatic pressure；pressure factor；abnormal high pressure；spontaneous production factor

作者简介：李传亮（1962-），男，山东嘉祥人，教授，博士，油藏工程，（Tel）028-83033291（E-mail）cllipe@qq.com

收稿日期：2015-08-26

文章编号：1001-3873（2016）02-0246-03

DOI：10.7657/XJPG20160223

中图分类号：TE618.13

文献标识码：A