气象无人机风速解算新模型的设计及仿真研究
李阳 孔毅 赵现斌(解放军理工大学气象海洋学院,南京 211101)
气象无人机风速解算新模型的设计及仿真研究
李阳孔毅赵现斌
(解放军理工大学气象海洋学院,南京 211101)
摘要:气象无人机探测过程中,风速矢量由无人机飞行参数解算得到,解算方法和对应参数的测量直接影响测风精度。从现有风速解算模型出发,考虑了气动角、欧拉角、航迹角,最终确定引入“航迹倾斜角”和“俯仰角”,建立了一种新的风速解算模型。模型推导过程中发现,当无人机平稳飞行时,航迹倾斜角、俯仰角是影响测风精度的关键因素。与现有模型相比,新模型能有效提高测风精度,当航迹倾斜角与俯仰角不等时,必须对风速偏差进行修正。基于新模型的测风误差仿真分析结果表明:存在某一角度,当偏流角小于该角时,风速误差受航迹倾斜角、俯仰角及偏流角共同影响;当偏流角大于该角时,风速误差受航迹倾斜角、俯仰角影响较小,该角的大小与传感器的测量值和误差值有关。
关键词:气象无人机,风速解算模型,航迹倾斜角,俯仰角,仿真
0 引言
高空风的探测对了解大气层的运动状况具有十分重要的意义,同时也是研究全球及区域气候变化、准确预报天气现象的重要手段。现有的高空风测量方法包括:气球法测风、风廓线仪测风、探空火箭测风、无人机测风。前三种测风法往往在小区域范围内探测垂直廓线,而无人机由于具有续航时间长、飞行高度高、机动性强、在危险环境中按指定航线探测等优点,可对大区域水平风场进行连续探测。为满足不同探测需求,以无人机为平台进行气象探测日益受到人们青睐。
目前气象无人机高空风探测方法主要包括水平空速归零法、解析测风法、航位推算法以及皮托管测风法。其中水平空速归零法要求无人机在高空水平面上盘旋飞行,不利于大区域、长航探测;解析测风法运算过程复杂,无法实时给出风场信息;航位推算法算法简单、较易实现,但测风精度低;皮托管测风法具有直接探测的优点,可对大区域进行连续测量,且估计频率相对较高,能够为无人机的飞行控制提供高精度的实时风参数。因此皮托管测风法是未来无人机测风技术的发展方向。
皮托管测风法的提出可追溯至1992年,澳大利亚气象局的Dr Greg Holland论证了可以用气象无人机携带皮托-静压管等有关仪器进行高空风探测[1],并于1995年在美国海军无人机研究办公室的支持下,推出了一系列高性能Aerosonde无人机。到目前为止,Aerosonde系列高性能无人机已多次成功跨越大西洋和南极考察,经受住恶劣天气的考验,获得大量有价值的气象数据。近年来,皮托管测风技术已经在国内外掀起新的研究高潮,如何进一步提高三维风场的测量精度是当前需要迫切解决的问题。已有的研究表明[2],气象无人机飞行姿态的不稳定性、运动状态的变化性、传感器的精度以及野值的处理方法是影响和制约测风准确度的关键因素。
随着无人机皮托管技术的不断进步,国内外研究人员开始考虑从无人机不同飞行状态出发,推导非惯性运动状态的测风模型[3-4],该过程测量仪器较多,探测成本高,而且引入更多的中间量,误差的传递性导致测量的波动性较大,不仅如此,无人机在实际运动过程中,往往加速中伴随着转动,推导出的单一的非惯性运动模型仍然存在局限性;另外,也有相关学者从地速测量入手,利用卡尔曼滤波法提高导航精度[5]。当前无人机地速采用GPS测得,其信号分为P码和C/A码,目前民用的为C/A码,定位误差在2.93~29.3m,测速误差为0.3m/s[6],因此,几乎可以忽略地速误差对测风精度的影响。鉴于此,本文在现有风速解算模型的基础上,忽略非惯性运动状态和地速误差对测风精度的影响,通过引入航迹倾斜角和俯仰角,将所测得的气流空速和航迹地速同时转换到地理坐标系中,提出一种基于气象无人机飞行姿态改进的测风模型。
1 风速解算模型
1.1现有风速解算模型
气象无人机测风原理[7-11]主要是通过探测仪器测量空速、地速,然后利用空速、地速、风速构成的矢量三角形关系解算风速。
空速测量原理是根据测得的静压、总压和温度,应用伯努利方程[12]和理想气体的状态方程得到空速va:
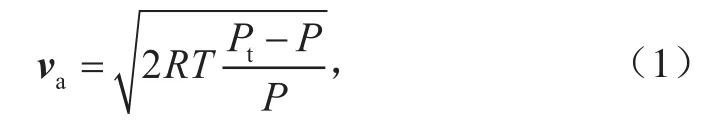
其中:va为空速(m/s);R为气体常数,R≈287m2/(K∙s2);T为静温(K);Pt为皮托-静压管测量的总压(Pa);P为静压(Pa)。静压和总压的测量均由安装在气象无人机上的皮托-静压管完成,总温的测量由温度传感器完成。
地速vg是根据机载GPS给出的无人机飞行参数,采用四星伪距定位法进行计算。
利用GPS与无人机携带的角度传感器测得的数据进行对比运算,可获得偏航角、航迹方位角等。空速、地速、风速三者构成的三角形关系[13]如图1所示。
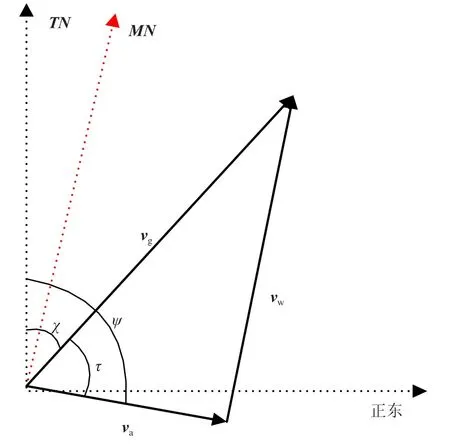
图1 水平面内速度矢量 三角形示意图Fig.1 Triangle chart of velocity vector in the horizontal plane
其公式为:
其中,TN为真北方向,MN为磁北方向,vw为风速(m/s),χ为水平航迹角,Ψ为偏航角,τ为偏流角。
理论上,现用测风模型计算的空速为气流坐标系中的空速,地速为航迹坐标系中的地速,利用空速、地速和风速构成三角矢量关系,需将气流空速和航迹地速同时转换到地理坐标系中再进行计算。而实际应用中为计算方便,简化了坐标系之间的角度关系,认为航迹坐标系、机体坐标系和地理坐标系重合[14],未对空速和地速进行相应的坐标变换,也未考虑坐标系间的角度关系对测风精度的影响。
1.2新型风速解算模型设计研究
鉴于现有风速解算模型存在的问题,本文利用坐标系间的变换关系[15-17],探讨了气动角、欧拉角、航迹角的引入,将现有气象无人机通过皮托管测量得到的空速以及无人机携带GPS设备测得的地速换算到地理坐标系中。其中,气动角表示气流坐标系与机体坐标系之间的角度关系,如图2a所示,包括攻角、侧滑角,攻角是机体纵轴与迎面气流之间的夹角,侧滑角是飞机速度矢量与机体纵向对称平面之间的夹角;欧拉角表示地理坐标系与机体坐标系之间的角度关系,如图2b所示,包括滚动角、俯仰角、偏航角,滚动角是机体横轴与水平面之间的夹角,俯仰角是机体纵轴与水平面之间的夹角,偏航角是机体纵轴相对预定航向在水平面内的偏转角;航迹角表示航迹坐标系与地理坐标系之间的角度关系,如图2c所示,包括水平航迹角、航迹倾斜角,水平航迹角是航迹速度矢量在水平面上的投影与正北方向之间的夹角,航迹倾斜角是航迹速度矢量与水平面之间的夹角。
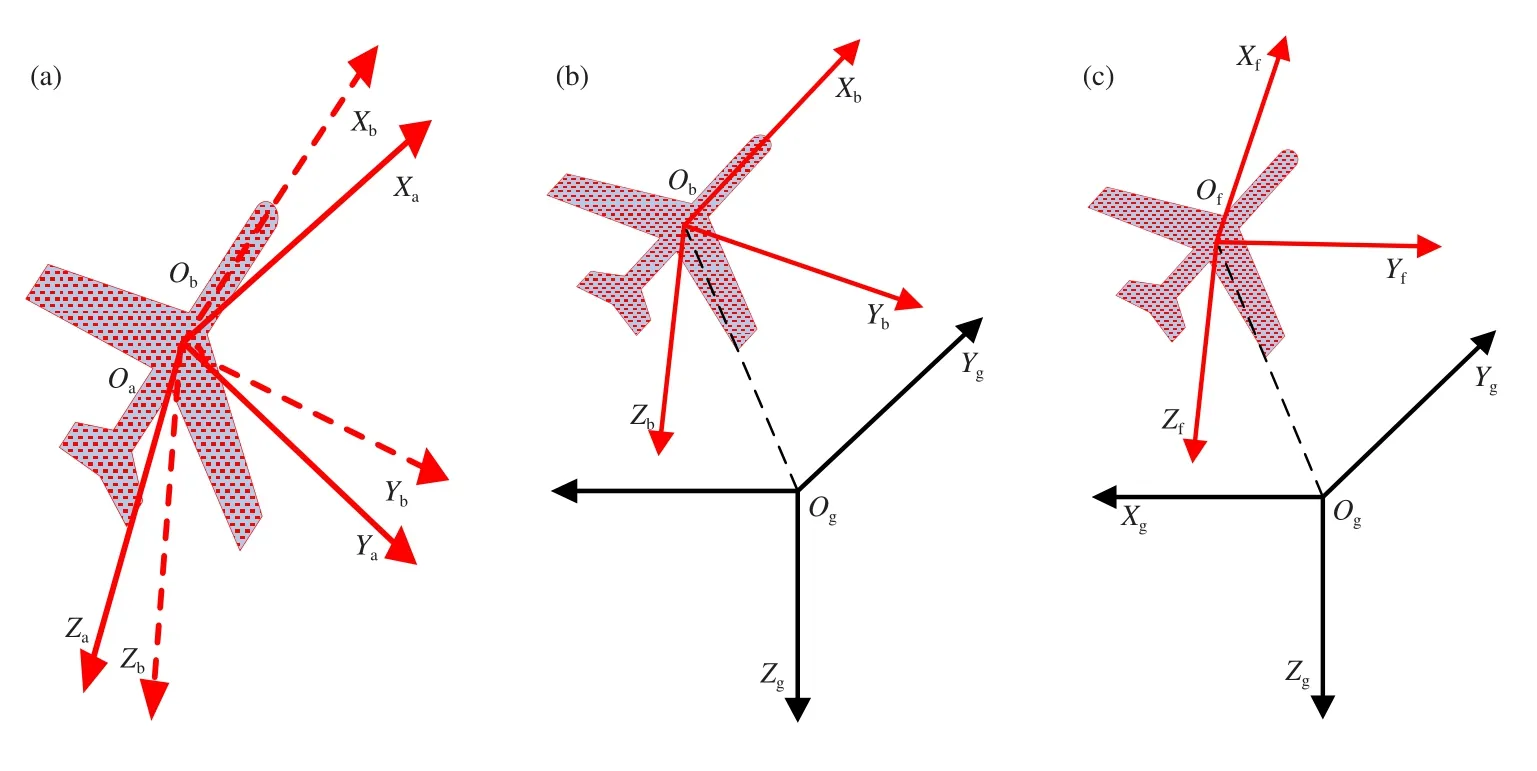
图2 气动角(a)、欧拉角(b)、航迹角(c)示意图Fig.2 Chart of pneumatic angle(a),euler angle(b)and flying track angle(c)
1.2.1气动角的探讨
无人机高空探测过程中,受气流扰动、飞机结构局部不对称以及机体重心位置偏差等因素的影响,导致皮托-静压管测量总压Pt实际为真实气流总压Pat的一个分量。通过引入气动角,可准确获取气流总压Pat,进而得到机体空速。
气流坐标系OaXaYaZa首先绕Za轴旋转β角,再绕Ya轴旋转-α角,得到机体坐标系ObXbYbZb,其中β为侧滑角,α为攻角。气流坐标系与机体坐标系之间的变换矩阵可表示为:
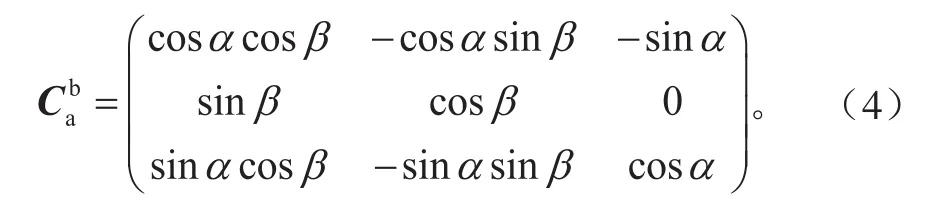
由于皮托管安装方向与机体纵轴方向一致,因此气流总压Pat在机体坐标系中可表示为:

测量总压Pt为Pat在机体坐标系中X轴方向的大小:
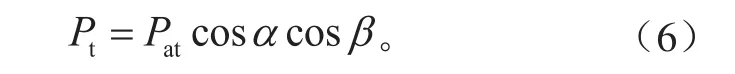
把式(6)代入理想模型的空速方程,得到气流坐标系下的空速大小:

根据气流坐标系与机体坐标系的变换关系,气流空速在机体坐标系中可表示为:
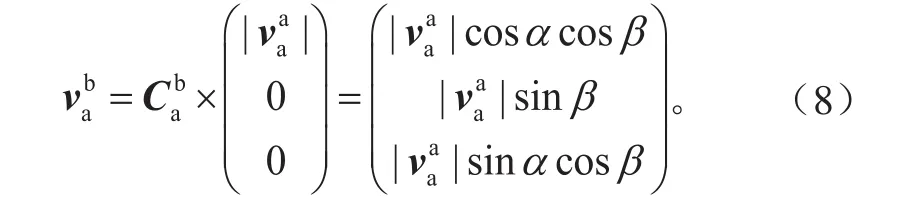
从数学模型的角度出发分析公式(8),当无人机在某一高度层平稳飞行时,其攻角和侧滑角一般较小(≤3°),可以得到,并且,因此可忽略其较小分量。同时在实际探测过程中,气象无人机高空飞行受气流扰动的影响,攻角和侧滑角的测量误差比较大,而且其校正又涉及到皮托管和无人机纵向轴线的对准校正、皮托管弯曲的校正、角速率影响的校正以及侧流和升流影响的校正,需要测量皮托管在不同加速度载荷下的弯曲率以及三个姿态角速率等参数。以上各参数的测量需要复杂的系统和解算过程,这在一定程度上增加了研制经费和时间,另外测量参数的增大也增加了输入误差源。因此在无人机水平探测时,可将式(8)近似表示为:

1.2.2 欧拉角的引入
通过引入欧拉角,可将机体空速转换到地理坐标系中。机体坐标系ObXbYbZb首先绕Xb轴旋转φ角,再绕Yb轴旋转θ角,最后绕Zb轴旋转-Ψ角,得到地理坐标系OgXgYgZg,其中φ为滚动角,θ为俯仰角,Ψ为偏航角。机体坐标系与地理坐标系之间的变换矩阵表示为:
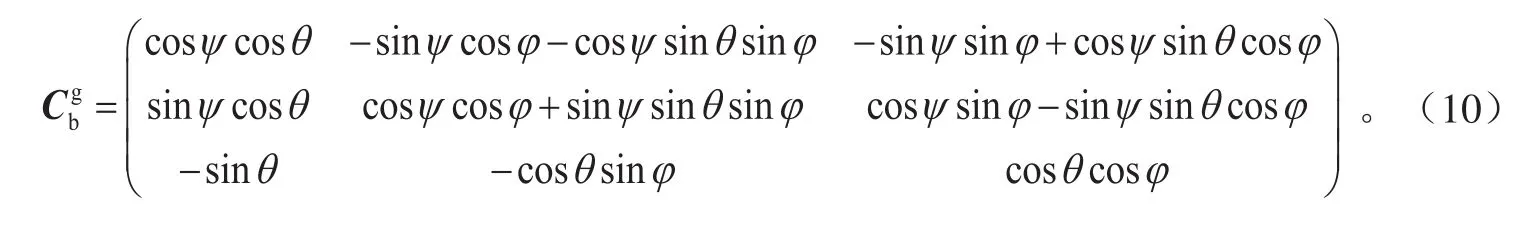
根据机体坐标系与地理坐标系的变换关系,机体空速在地理坐标系中可表示为:

1.2.3航迹角的引入
通过引入航迹角,可将航迹地速转换到地理坐标系中。航迹坐标系OfXfYfZf绕Yf轴旋转δ角,再绕Zf轴旋转χ角,则得到地理坐标系OgXgYgZg,其中χ为水平航迹角,δ为航迹倾斜角。航迹坐标系与地理坐标系之间的变换矩阵为:
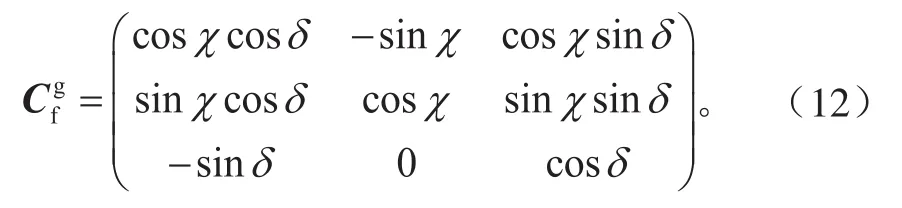
根据航迹坐标系与地理坐标系的变换关系,航迹地速在地理坐标系中可表示为:

1.2.4风速方程的构建
地理空速、地理地速、地理风速在地理坐标系中构成三角形矢量关系:

其中:vw为求解的风速(m/s)。在地理坐标系中,风速最终可表示为:

公式(16)为基于气象无人机飞行角度的风速解算改进模型。上式表明,相对于现有的风速解算模型而言,本文中的新模型仅引入了“航迹倾斜角”和“俯仰角”。
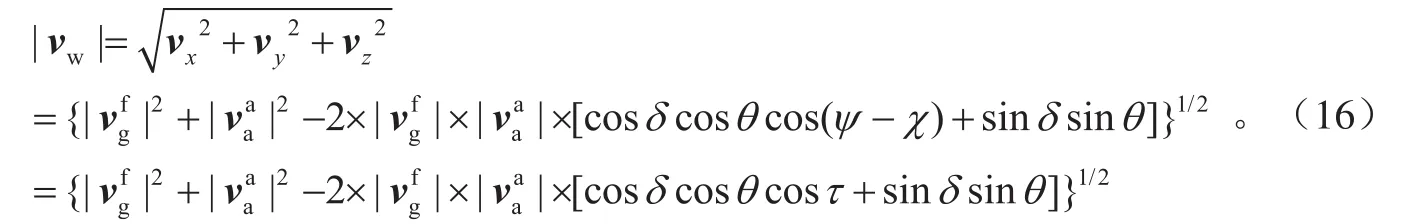
2 模型对比分析
为验证改进模型的准确性,分别从实验论证和仿真模拟的角度,对两者进行对比,同时指出风速偏差随着航迹倾斜角、俯仰角及偏流角变化的规律。
2.1实验论证
现以某无人机大队于2008年4月17日气象探测数据为例,采集飞行高度为5000±20m的数据,并对数据进行预处理,带入现有模型以及改进模型中。由于用GPS和测风雷达跟踪的气球测风法探测精度和探测高度最高,因此将风速解算数据与同一时间同一区域气球法测量的5000m高度的风速进行对比,如图3所示。
由图3可知:通过本次实验数据验证发现,1)改进模型的风速解算值大于或等于现有模型;2)改进模型的风速值在14.5m/s处上下波动,相对于现有模型更接近于气球法测量值。实验显示改进的风速解算模型优于现有模型。

图3 风速解算值对比Fig.3 Comparison of wind speed resolution
现对照探测数据以及风速解算值,发现当航迹倾斜角和俯仰角大小接近时,风速偏差较小,而当航迹倾斜角和俯仰角相差较大时,风速偏差较大,需使用改进模型进行修正。同时当航迹倾斜角、俯仰角不变,风速偏差随着偏流角的增大而减小。
2.2仿真模拟
上述实验验证了改进模型相较于现有模型测风精度更高,现从仿真模拟角度,对两种模型进行差值计算,分析航迹倾斜角、俯仰角及偏流角对测量精度的影响,间接论证引入航迹倾斜角、俯仰角的必要性。考虑到新模型在现有模型基础上引入了航迹倾斜角、俯仰角,因此仿真在不同偏流角情况下,由航迹倾斜角和俯仰角共同引起的风速偏差。
气象无人机在风速测量过程中,地速和空速的变化范围较小,假设航迹地速=50m/s,气流空速=40m/s,航迹倾斜角δ的变化范围为-5°~5°,俯仰角θ的变化范围为-5°~5°,在偏流角τ分别取10°,20°,30°的情况下,风速偏差随航迹倾斜角和俯仰角的变化曲面如图4所示。
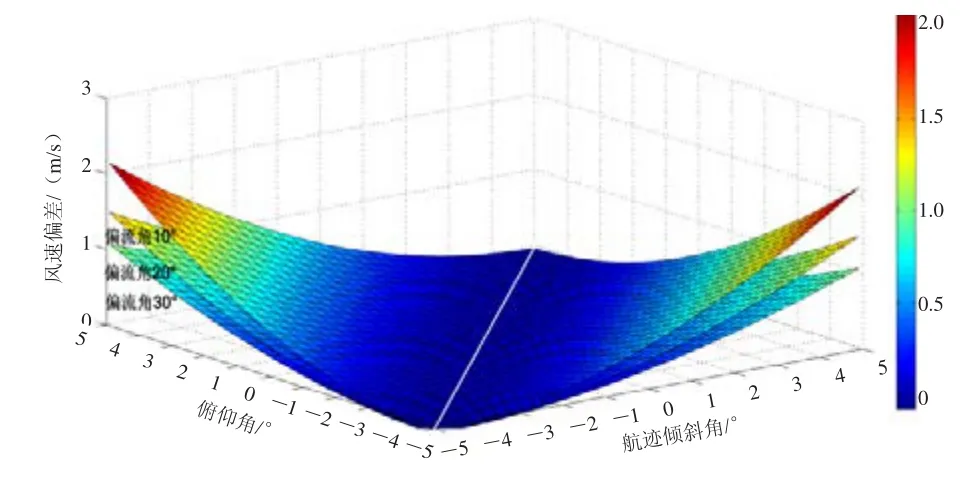
图4 角度引起的风速解算偏差Fig.4 Deviation of wind resolution models caused by the angles
由图4可以看出:1)取航迹倾斜角与俯仰角上的等值点构建一条等值线,如图中白线所示,由角度引起的风速偏差相对于该等值线对称;2)当航迹倾斜角与俯仰角相等时,风速偏差最小;3)在航迹倾斜角和俯仰角不变的情况下,随着偏流角的增大,风速偏差逐渐减小;4)当取等值线左侧,在同一航迹倾斜角的情况下,风速偏差随着俯仰角的增大而增大,当取等值线右侧,在同一情况下,风速偏差随着俯仰角的增大而减小;5)同样,取等值线左侧,在同一俯仰角的情况下,风速偏差随着航迹倾斜角的增大而减小,取等值线右侧时,在同一情况下,风速偏差随着航迹倾斜角的增大而增大;6)改进模型的风速测量值大于现有模型。
仿真结果说明:1)风速偏差对偏流角、航迹倾斜角、俯仰角的大小较敏感,当航迹倾斜角与俯仰角取值相等时,其风速偏差最小。由于无人机飞行过程中受气流扰动影响,航迹倾斜角与俯仰角的大小无法控制,呈无规律变化,因此需在现有风速解算模型中加入航迹倾斜角和俯仰角进行修正。2)现有模型风速解算值往往小于真实值,改进模型实际是在现有模型测量值的基础上加上一个正修正量,其大小与姿态角的正余弦值相关。3)当不考虑航迹倾斜角以及俯仰角情况下,即两者同时为0时,改进的风速解算模型与现用测风模型相同,反证改进模型是在现有模型基础上引入航迹倾斜角和俯仰角两个量,说明改进模型推导过程是正确的。
3 风速误差分析
3.1误差计算模型
误差分析采用标准差形式进行分析。假设各输入误差均服从正态分布,且互不相关,则改进型测风模型中风速误差标准差为:
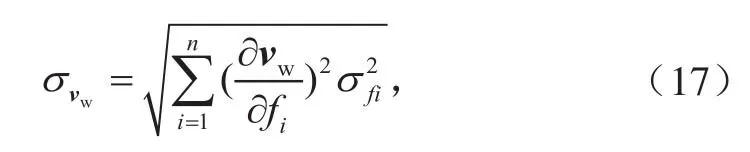
其中,航迹地速、气流空速、航迹倾斜角、俯仰角、偏航角、航迹方位角误差引起的风速误差分别为:
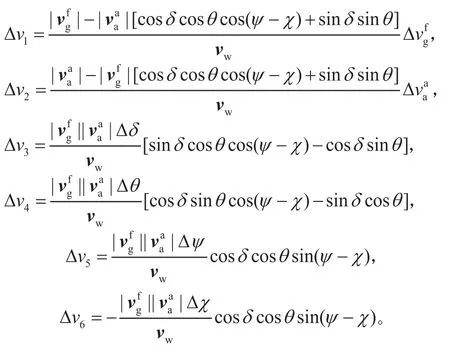
由航迹地速、气流空速、航迹倾斜角、俯仰角、偏航角、航迹方位角引起的风速误差标准差为:

式(18)即为航迹地速、气流空速、航迹倾斜角、俯仰角、偏航角、航迹方位角引起的风速误差标准差计算式,式中,,,,,,分别为航迹地速、气流空速、航迹倾斜角、俯仰角、偏航角、航迹方位角的误差标准差。可以看出,风速误差包括六项误差分量,按照几何和的形式合成得到总误差。
3.2误差分析
由误差计算模型可知,无人机测风精度是飞行参数及其测量误差等多种因素共同作用的结果。现假设航迹地速=50m/s,气流空速=40m/s,本文拟根据现有误差模型对航迹倾斜角和俯仰角引起的测风误差进行仿真分析。其飞行参数和相应测量误差见表1。

表1 无人机瞬时飞行参数及误差表Table 1 UAV instantaneous flight parameters and error
综合考虑各参数值的测量误差,带入误差计算模型,得到在不同偏流角情况下,由航迹倾斜角和俯仰角引起的风速误差示意图,图5a为偏流角≤10°时,角度引起的风速误差;图5b为偏流角>10°时,角度引起的风速误差。

图5 偏流角≤10°时(a)和偏流角>大于10°时(b)角度引起的风速误差Fig.5 The case of drift angle is less than or equal 10°(a)or more than 10°(b)
对比图5a和5b得知,1)该仿真以10°为界,当偏流角<10°时,风速误差变化规律相似,呈三维抛物线状,等值线上的点误差值最小;当偏流角>10°时,不同偏流角对应不同的风速误差,且同一偏流角情况下,风速误差约等于某一定值。其中,对于不同的仿真模型,界定角的大小不同,为准确获取界定角,将空速、地速以及测量误差带入公式(18),得到只包含偏流角、航迹倾斜角及俯仰角的风速误差计算公式。利用偏微分方程,求解风速误差模型的切平面方程。对切平面方程进行解析,发现存在一个界定角,当偏流角大于等于该角时,对于任意一点的切平面斜率约等于零,即风速误差为定值,当偏流角小于该角时,风速误差是航迹倾斜角、俯仰角、偏流角共同作用的结果。2)当偏流角取较小或较大值时,风速误差相对较小。即无人机顺风、逆风飞行或当无人机运动方向与风向垂直时,风速误差相对较小。
我国气象探测要求风速误差在10%以内,大量数据显示5000m高度风速在14~22m/s,为提高测风精度,联系误差计算模型,可将风速误差控制在1.4m/s以内。现提出提高测风精度的两条途径:一是对探测数据进行处理,剔除由加速、转动、上升幅度过大造成的较大偏差且在新模型中又无法相互抵消的值;二是通过提前估算高空风向,控制无人机机轴与风向的夹角。由于高空气流的扰动以及无人机运动的复杂性,使得无人机很难满足机轴方向与风向平行或垂直,因此对探测数据进行处理和修正是提高测风精度的关键任务。
参考文献
[1]Holland G J,Webster P J,Curry J A,et al.The Aerosonde Robotic Aircraft:A new paradigm for environmental observations.Bulletin of the American Meteorological Society,2001,82(5):889-902.
[2]Hou J.Analysis on structure and characteristics of pitot type flowmeter.Journal of Xinjiang University(Natural Science Edition),2005,22(2):189-193.
[3]周树道,王彦杰.基于非惯性运动状态的气象无人机测风方法研究.传感器学报,2011,24(1):155-158.
[4]王彦杰,周树道.基于转动状态的气象无人机测风方法.气象科学,2011,31(5):576-581.
[5]刘伟.基于惯性/多普勒组合导航的风速风向测量研究.南京:南京航空航天大学,2011.
[6]李天文.GPS原理及应用.北京:科学出版社,2003.
[7]Haering E A.Air Data Calibration of a High-Performance Aircraft for Measuring Atmospheric Wind Profiles.NASA Technical Memorandum 101714,1989.
[8]World Meteorological Organization.Aircraft Meteorological Data Relay(AMDAR)Reference Manual.Geneva:WMO,2003.
[9]Klopfenstein R.Air velocity and flow measurement using a pitot tube.ISA Transactions,1998,37(4):257-263.
[10]Bouhy J.Evolution of the pitot tube sensor.Flow Measurement Technology in Practice,1996,21(1):1-4.
[11]Thomas D.Make the most of averaging pitot tubes.Chemical Processing,2005,68(7):33-35.
[12]潘锦珊.气体动力学基础.北京:国防工业出版社,1989.
[13]周伟静,沈怀荣.磁偏角对无人机皮托-静压管测风的影响分析.装备指挥技术学院学报,2006,17(4):97-101.
[14]张志远,罗国富.舰船姿态坐标变换及稳定补偿分析.舰船科学技术,2009,31(4):34-40.
[15]成旭晟.矢量变换控制的分析及仿真.工业科技,2009,38(2):49-50.
[16]徐忠富,王国良,尹照武,等.基于UML的空间位置和坐标变换建模方法.计算机工程,2009,35(16):42-44.
[17]常明飞.GPS/SINS组合导航系统研究.重庆:重庆大学,2007.
A New Method of Meteorological UAV Wind Velocity Resolution Model Design and Simulation
Li Yang,Kong Yi,Zhao Xianbin
(Institute of Meteorology and Oceanography,PLA University of Science and Technology,Nanjing 211101)
Abstract:In the meteorological UAV detection,wind velocity vector is resolved from UAV flying parameters.The detected velocity accuracy is directly affected by the resolution method and the detection measurement of corresponding parameters.Starting from existing wind resolution models,this paper set up a new wind velocity resolution method which has introduced flying track tilt angle and pitch angle in view of pneumatic angle,euler angle and flying track angle.It is discovered in the model derivation procedure that when the UAV flies stably,flying track tilt angle and pitch angle are the key factors which affect the accuracy for wind velocity accuracy.Compared with existing models,the new model can improve wind detection accuracy effectively,when the flying track tilt angle unequals the pitch angle,the wind speed deviation must be corrected.Detecting error result proves that there exists one angle affected by the detecting value and error value of the sensor.When drift angle is smaller than this angle,wind velocity error is mutually affected by flying track tilt angle,pitch angle and drift angle.When drift angle is bigger than itself,wind velocity error is less affected by flying track tilt angle and pitch angle.
Keywords:meteorological UAV,wind velocity resolution model,flying track tilt angle,pitch angle,simulation
通信作者:孔毅(1954—),Email:qyqxxy123@sina.com
收稿日期:2014年8月16日;修回日期:2015年2月9日
DOI:10.3969/j.issn.2095-1973.2016.01.005
第一作者:李阳(1987—),Email:412481016@qq.com
 Advances in Meteorological Science and Technology2016年1期
Advances in Meteorological Science and Technology2016年1期
- Advances in Meteorological Science and Technology的其它文章
- 榜单
- 风电功率预报技术研究综述
- 利用城市夜间灯光资料和NDVI研究成都地区植被覆盖度变化
- 谈谈统计预报的必要性
- 模拟热浪及强降温对Apo E-/-小鼠冠心病影响的实验研究
- 山东省夏季降水的年代际变化和年际变化
