一种基于Burg谱估计和FFT的频偏估计方法

陈　伟,邢依依,刘梦婷

(西安电子科技大学 电子信息攻防对抗与仿真重点实验室,陕西 西安　710071)



一种基于Burg谱估计和FFT的频偏估计方法

陈伟,邢依依,刘梦婷

(西安电子科技大学 电子信息攻防对抗与仿真重点实验室,陕西 西安710071)

摘要针对星间链路通信中常用的BPSK、QPSK、UQPSK和64QAM等调制信号的载波频偏估计问题,提出了一种基于Burg谱估计和FFT的通用频偏估计方法。采用Burg谱估计方法对信号进行粗频偏估计,补偿该频偏后得到含有较小残留频偏的信号;并进行改进的四次方非线性变换,去除调制信息;再利用FFT估计出较高精度的残留频偏值。仿真结果表明,该方法估计精度高、范围大。

关键词星间链路通信;频偏估计;Burg谱估计;FFT

A Frequency Offset Estimation Algorithm Based on Burg Spectrum Estimation and FFT

CHEN Wei,XING Yiyi,LIU Mengting

(Key Laboratory of Electronic Information Countermeasure and Simulation,Xidian University,Xi’an 710071,China)

AbstractA general frequency offset estimation method of BPSK,QPSK,UQPSK and 64QAM signals based on Burg spectrum estimation and FFT is proposed to solve the carrier frequency offset estimation of common signals in inter satellite link communication.First,the coarse frequency offset estimation is obtained by using the Burg spectrum estimation method,and the signal of the residual frequency offset is obtained after the compensation of the frequency offset.Then the improved fourth non-linear transformation is used to remove modulated information.Finally,the residual frequency offset value is estimated by FFT.Simulation results show that this method is of high accuracy and wide acquisition range.

Keywordsinter satellite link communication;frequency offset estimation;Burg spectrum estimation;FFT

MPSK和MQAM这两类调制信号以其高的频带利用率和良好的抗噪性能,目前已在卫星无线通信系统中得到广泛应用。由于多普勒频移和收发双方振荡器不稳定等因素的影响,使得接收机接收信号的载波与本地载波存在较大动态范围的频偏,而载波恢复是通信信号接收的一项关键技术,其恢复效果将直接影响接收机信号接收的性能[1]。

对于MPSK和MQAM信号的频偏估计,前人做了大量的研究。文献[2]提出一种对MPSK信号进行频偏估计的简单方法,称为MAT算法,通过对MPSK信号作M次方运算用于去除相位调制信息,得到频率为M×Δf(Δf为频偏)的正弦波信号,再估计出该正弦波的频率并除以M即可得到原信号的频偏估计值。文献[3]对低通滤波后的MPSK信号,采用现代功率谱估计算法对频率做初步估计[4],再通过M次方非线性变换[5],根据最大似然准则,寻找其最优解,算法可在较低信噪比下比较准确地恢复出载波频偏,这些算法均需要已知信号的调制类型来确定M的大小。文献[6]提到M-QAM信号进行4次方变换后,其频谱中含有4倍载频分量的谱线,据此可估计信号的载频。文献[7]提出首先利用FFT对较短数据频偏进行快速粗估计,获得大的频偏估计范围,然后通过对残余频偏进行非线性变换和数据抽样变换,该算法可获得较高的频偏估计精度以及较宽的估计范围,但该算法利用FFT对MPSK信号进行频偏粗估计的精度不高,可能会对后续的精确估计产生影响。

根据上述分析,本文主要针对星间链路通信中常用的BPSK、QPSK、UQPSK和64QAM调制信号作分析,由于事先不确定信号的调制类型,但未知信号的调制类型是其中的一种,本文通过采用现代谱估计中的Burg算法、改进的4次方去调制和FFT相结合的方法对该未知信号进行频偏估计。

1调制信号的数学模型

1.1MPSK信号模型

假设接收信号是在高斯信道下,已完成定时同步。MPSK的信号模型假设为

x(k)=akej(2πΔfkT+θ)+n(k),k=0,1,2,…,N-1

(1)

式中,ak=ej2πi/M,i=0,1,…,M为调制数据序列;Δf为待求的载波频偏;θ为载波相位;T为符号周期;n(k)是零均值的复高斯白噪声,N为信号长度。显然,当M=2时为BPSK信号;M=4时为QPSK信号。

1.2UQPSK的信号模型

UQPSK信号是非均衡的QPSK信号,与QPSK信号的区别在于正交的两路信号幅度和功率不等,其信号模型为

(2)

1.364QAM信号模型

64QAM信号为64正交幅度调制信号,是一种振幅和相位联合键控。在QAM体制中,信号的振幅和相位作为两个独立的参量同时受到调制,64QAM的信号模型为

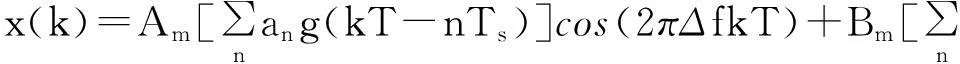
(3)

式中,Am={1,3,5,7},Bm={1,3,5,7},共64种幅度组合。

2算法描述

2.1基于Burg谱估计的频偏估计模型

Burg提出使用线性预测的方法来递推计算不同阶数预测器的系数,然后比较各预测器的误差功率[8]。算法的实现是基于Levinson-Durbin递推,其具体思路为首先求解出观测序列的自相关系数矩阵,然后在此基础上采用Levinson-Durbin递推,求解AR模型的参数。

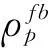
(4)

本文利用Burg算法进行频偏粗估计的步骤如下:

步骤1采用最终预测误差(FPE)准则来确定阶次:取式(5)最小值所对应k值作为模型阶次p。

(5)

(6)

(7)

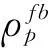
am(k)=am-1(k)+kmam-1(m-k),k=1,2,…,p

am(m)=km

(8)

(9)

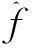
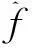
(10)

其中,为fs为信号采样频率,N为FFT点数。

2.2频偏估计方法

文献[2]提到通过对MPSK信号作M次方运算可去除相位调制信息,得到频率为M×Δf的正弦波信号。显然,对BPSK信号或QPSK信号作4次方运算可得到频率为4×Δf的正弦波信号;文献[6]提到通过对M-QAM信号进行4次方变换后,其频谱中含有4倍载频分量的谱线。显然,64QAM也包含在内;而对于UQPSK信号,通过仿真发现,当均衡因子在0~0.27或0.35~0.5之间时,对UQPSK信号进行4次方变换后,其频谱中含有4倍载频分量的谱线,而当均衡因子在0.27~0.35之间时,4次方非线性变换后,频谱没有单独的4倍载频分量谱线,但经过6次方非线性变换后,频谱出现6倍载频分量谱线,但此时信号的信噪比损失变大。

通过上述分析可知:对BPSK,QPSK,UQPSK(≠0.27~0.35)和64QAM调制信号进行4次方非线性变换后,其频谱中将含有4倍载频分量的谱线。为最大限度地降低噪声,提高输出信噪比,可对上述变换作改进,基于改进的4次方变换和FFT的频偏估计的具体步骤如下:

步骤1根据噪声不相关和正弦信号的相关特性,可将4次方变换改为对信号延时后与原信号相乘,再做平方运算

x′4(n)⟹(x′(n-1)x′(n))2

(11)

步骤2对其做N点FFT,得到频谱,搜索其谱峰值点,得到峰值的index1值,继而由下式求出x′(n)的载波频偏估计值

(12)

2.3总体频偏估计算法

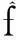
(13)

3算法仿真结果与性能分析

应用Matlab软件对上述算法进行仿真分析。选取BPSK、QPSK、UQPSK和64QAM调制信号为对象,设定信号的载波频率f=1.05GHz+Δf,中心频率为1.05GHz,频偏Δf分别设1MHz、10MHz、50MHz和100MHz,码速率frate为10Mbit·s-1,采样频率fs为600MHz,信号长度N为4 096点,Burg谱估计取前2 048点即可,其中UQPSK的均衡因子α设为0.4。仿真过程中先对信号进行数字正交下变频变换到复基带(I/Q),然后再作频偏估计,信噪比SNR选取范围设为-7~10dB,分别对上述4种信号进行100次蒙特卡洛实验,得到各信号载波频偏估计的绝对值误差曲线如图1~图4所示。

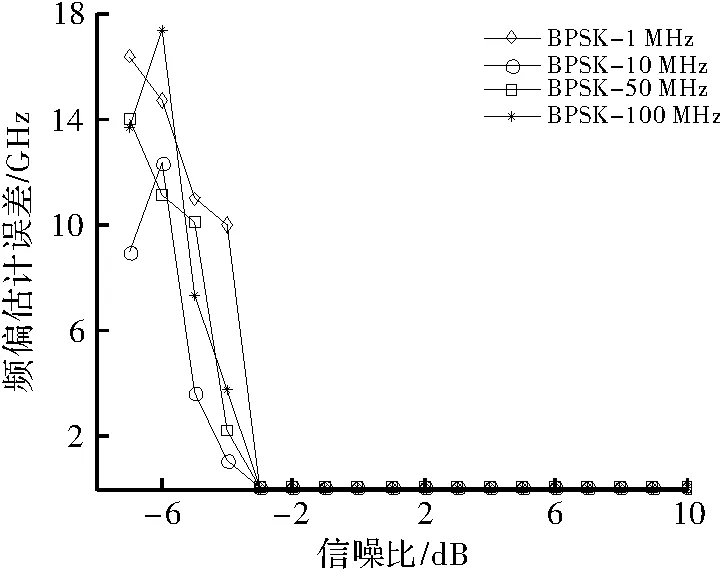
图1　BPSK信号频偏估计误差曲线

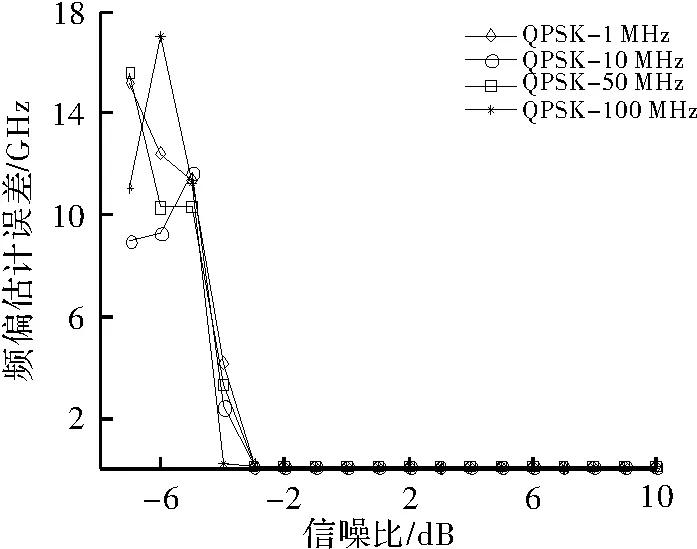
图2　QPSK信号频偏估计误差曲线

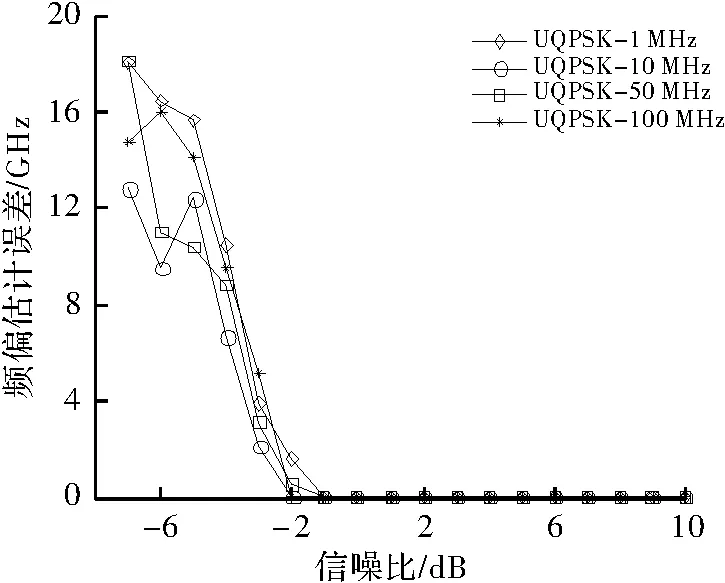
图3　UQPSK信号频偏估计误差曲线

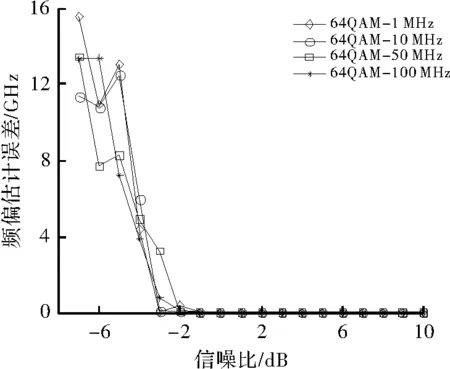
图4　64QAM信号频偏估计误差曲线

信号经过下变频变换到复基带信号后的频率分辨率为fs/2/(4N)=18.310 5 kHz,即估计出来的频偏值误差的绝对值<9.155 3 kHz,显然,频偏估计的精度只与算法的参数有关,则信号长度N的大小可根据系统对频偏估计精度的要求来选择。由上述对4种信号的频偏估计误差仿真图可知,当信噪比SNR≥-3 dB时,该算法可准确地估计出BPSK和QPSK调制信号的频偏值;当信噪比SNR≥-1 dB时,该算法可准确地估计出UQPSK和64QAM调制信号的频偏值。由于采用了Burg谱估计对信号进行频偏粗估计,所以频偏估计范围得到了较大的扩展。由此可得知,本文频偏估计算法在信噪比SNR≥-1 dB条件下,可准确地估计出该未知调制类型信号的频偏值。

4结束语

本文提出了基于Burg谱估计、改进的MAT算法和FFT相结合的频偏估计算法,通过理论分析和仿真实验,结果表明该算法在较低的信噪比条件下能准确的对星间链路通信中常用的BPSK、QPSK、UQPSK(α≠0.27~0.35)和64QAM调制信号进行频偏估计,并且能够同时兼顾频偏估计精度和估计范围,适合于工程应用,但由于UQPSK调制信号在均衡因子α为0.27~0.35时不适用于本文通用算法,具体解决方法还待进一步研究。

参考文献

[1]刘晓冬,陈卫东.一种宽范围高精度的载波频偏估计算法[J].无线电工程,2014,44(3):43-45.

[2]Mounir Ghogho,Ananthmm Swami,Tariq Durrani.Blind estimation of frequency offset in the presence of unknown multipath[C].Piscataway,NJ,USA:2000 IEEE International Conference on Personal Wireless Communications,IEEE,2000.

[3]崔艳鹏,胡建伟,杨绍全,等.一种低信噪比下MPSK信号频率估计方法[J].西安电子科技大学学报:自然科学,2011,38(5):90-94.

[4]Gu Huaijin.Frequency resolution and estimation of AR spectral analysis[J].IEEE Transactions on Signal Processing,1993,41(1):432-436.

[5]Viterbi A J,Viterbi A M.Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmission[J].IEEE Transactions on Information Theory,1983,29(4):543-551.

[6]詹亚锋,曹志刚,马正新.M-QAM信号的调制制式识别[J].通信学报,2004,25(2):68-74.

[7]谭晓衡,张毛.一种高精度的改进FFT频偏估计算法[J].重庆理工大学学报:自然科学,2010,24(7):71-75.

[8]简秦勤.直扩信号的检测与恢复[D].西安:西安电子科技大学,2013.

[9]张威,张路纲.Burg算法最大熵谱估计的VC++仿真分析[J].北京石油化工学院学报,2002,10(3):16-18.

中图分类号TN927+.3

文献标识码A

文章编号1007-7820(2016)03-160-04

doi:10.16180/j.cnki.issn1007-7820.2016.03.042

作者简介:陈伟(1991—),男,硕士研究生。研究方向:通信侦察信号处理,电子对抗。

收稿日期:2015- 08- 06