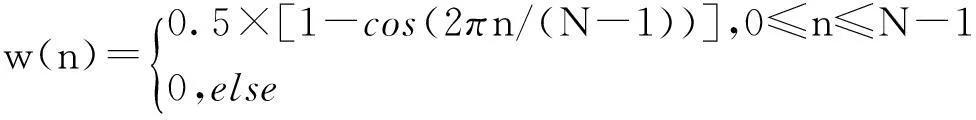基于改进小波包变换的音频指纹提取算法

朱　洁,邓开发

(1.上海理工大学 光电信息与计算机工程学院,上海　200093;2.上海工程技术大学 艺术设计学院,上海　200093)



基于改进小波包变换的音频指纹提取算法

朱洁1,邓开发2

(1.上海理工大学 光电信息与计算机工程学院,上海200093;2.上海工程技术大学 艺术设计学院,上海200093)

摘要数字音频指纹技术在音频信号分析和处理中起着重要作用。针对传统基于时频分析的音频指纹提取算法中仅使用信号能量作为特征参数,而无法全面表征出信号的复杂度和不规则性问题,提出了基于小波包分解与重构,将小波包系数的奇异值熵和样本熵相结合,作为音频信号的特征参数提取指纹。实验证明,该算法提取的指纹提高了音频识别的准确率,在常见信号处理下能保持较强的鲁棒性,并具有明显的区分音频和定位音频篡改位置的能力。

关键词音频指纹;小波包分解;奇异值熵;样本熵;特征提取

An Approach to Audio Fingerprinting Extraction Based on Improved Wavelet Packet

ZHU Jie1,DENG Kaifa2

(1.School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;2.School of Art and Design,Shanghai University of Engineering Science,Shanghai 201620,China)

AbstractDigital audio fingerprinting technology plays an important role in the audio analysis and processing.Aiming at the problem that the traditional audio fingerprinting is extracted based on time frequency analysis using the energy of signal as a single feature parameter that can not fully characterize the complexity and irregularity,the paper proposes a method for audio fingerprinting extraction based on wavelet packet decomposition and reconstruction and combining the sample entropy of wavelet packet coefficients and the entropy singular value as a signal characteristic parameters to extract audio fingerprinting.Experimental results show that the proposed algorithm is accurate in audio recognition,robust in common audio signal operations,and capable of distinguishing different audio and locate tampered position.

Keywordsaudio fingerprinting;wavelet packet decomposes;entropy of singular values;sample entropy;feature extraction

近年来,基于内容的音频检索(Content-Based Audio Retrieval,CBAR)技术出现了许多新的研究和发展方向,而音频指纹(Audio Fingerprinting,AF)技术是 CBAR 的关键技术之一,其主要目的是建立一种有效机制来比较两个音频数据的听觉质量,是从音频中提取的具有音频声学特征的紧致数字签名。AF基金项目:南京市领军型科技创业人才引进计划基金资助项目(No.2014A090002)技术在数字音频内容的音频内容识别、版权保护、内容完整性校验等领域都具有广泛的应用价值,逐渐成为国内外学者研究的热点。

学术界对音频指纹技术的研究主要包括基于时域音频指纹算法、频域音频指纹算法和时频域音频指纹算法[1]。为更好的处理非平稳随机信号和具有频谱时变性的确定信号,目前研究最多的是基于时频分析的音频特征提取算法,如短时傅里叶变换、小波变换、小波包分解和经验模式分解(EMD)等,其目的是将一维的时域信号或频域信号映射成时-频域上的二维信号来处理。多数指纹提取算法基于以下方法:将音乐信号分成互相重叠的帧,对每个帧计算一系列特征,此类特征需要对各种音频信号处理在一定程度上保持不变。文献[2~3]用子带正规化方法来研究音频识别的调制频率特征,文献[4]提出了基于3种鲁棒哈希函数,其中SVD-MFCC性能最佳。

然而,传统基于时频分析的方法在音频特征提取上存在一定的局限性,包括原始信号经小波包变换,得到的由时间轴和频率轴所构成的二维时频信息矩阵维数过大,需要对时频矩阵信息再次甚至多次处理,才能有效提取反映信息矩阵内在特征的特征变量。因此,考虑引入非线性参数估计方法来提取隐藏在时频矩阵中的信号特征。常用的非线性参数主要有信号的能量、分形维数和熵等。

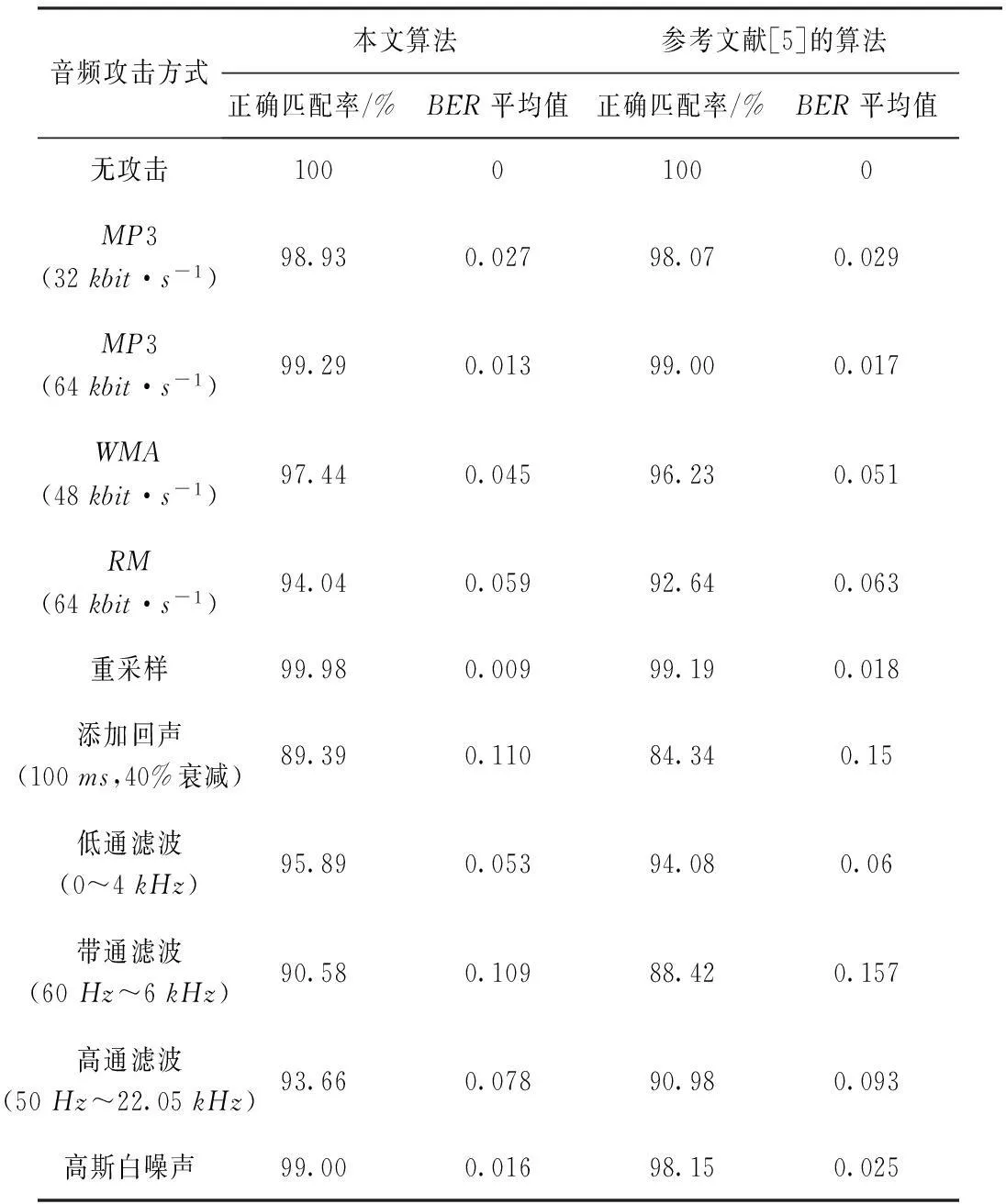
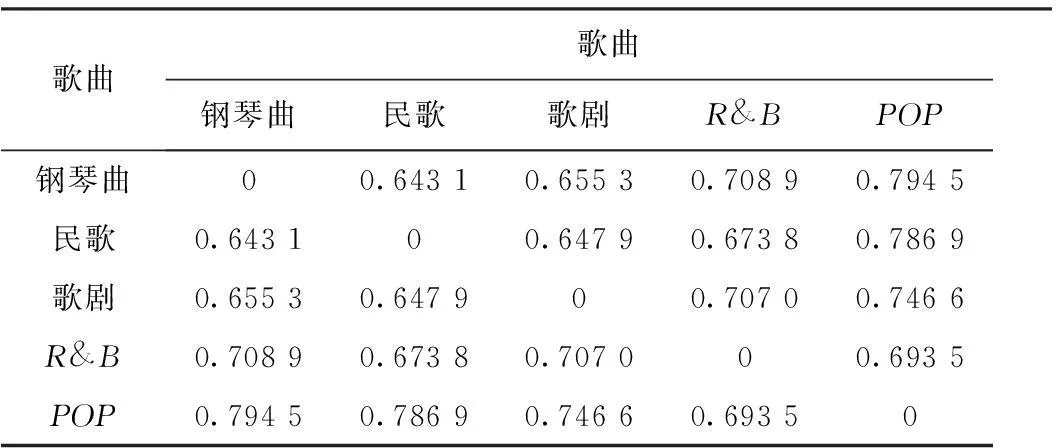
本文将奇异值熵和样本熵引入音频指纹提取中,提出一种基于小波包变换,采用奇异值熵和样本熵相结合的特征向量作为表征音频信号时频矩阵系数的特征参量,再通过统计值计算提取音频指纹。初步实验结果表明,对音频鲁棒性检测的误码率低于0.11,与文献[5]中的0.13相比,达到了很好的鲁棒性。对不同歌曲之间指纹比对的误码率均高于0.64,优于文献[5]中的指纹距离0.5的阈值目标,证明该算法在不同音频间具有很强的可区分性。

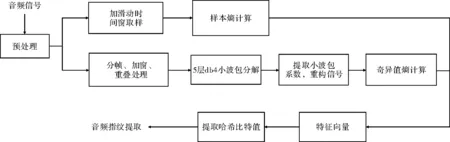
1指纹提取

1.1小波包分解与特征矩阵提取

特征提取是音频指纹生成的关键步骤。在实际音频信号,尤其是非平稳音频信号的处理中,信号任意时刻的频域特征较为重要。因此,需要使用能将时域、频域信息结合起来,用于描述信号的时频分析方法。小波包分析是一种比小波分析更为精细的分解方法,不仅继承了小波变换的多分辨率分析[6]形式,并可实现对信号进行各频带相互衔接、正交和无冗余的分解,可见小波包分析具有更广泛的应用价值。

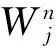
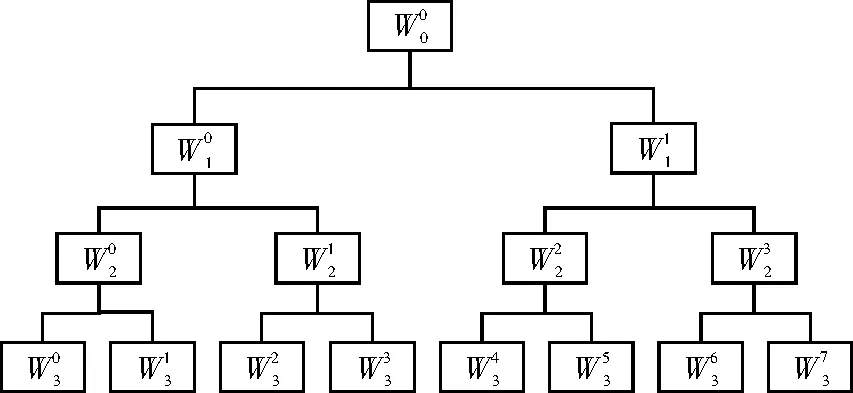
图1　3层小波包分解的树结构

在小波包分解中,分解层数的增加可使信号的高频成分和低频成分的分解都达到很精细的程度,且每级尺度的不同小波包分解系数,对信号的表征程度不同。

因此,本文采用对音频信号S进行5层小波包分解,小波基采用db4小波,将小波包分解系数作为描述信号的特征,只需通过少量系数就能对信号进行很好的刻画,分解后的第5层空间将包含32个子空间,即

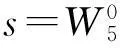
(1)

分别提取第5层从低频到高频各频带成份的小波包分解系数,对所有已得小波包系数进行重Sj(j=0,1,2,…,25-1)表示第5层各节点小波包系数的重构信号,构建信号的特征矩阵为

(2)

1.2奇异值分解及奇异值熵计算

奇异值是矩阵所固有的特征,奇异值可充分地反映矩阵中所含的信息。小波包的奇异值熵是基于奇异值分解理论,将信号经小波包变换后的系数矩阵分解为一系列能反映原系数矩阵基本特征的奇异值,再利用信息熵的统计特性对奇异值集合进行不确定度分析,从而对音频信号的复杂程度给出一个确定的量度。因此,可采用小波包空间特征矩阵A的奇异值作为音频信号的特征,构建特征向量,方法如下[7]:

设A是m×n(假定m>n)矩阵,秩为r(r≤n),则存在m×m正交阵U和n×n正交阵V,使得UΛVT=A(或UΛVH=A),其中,Λ为m×n的非负对角阵

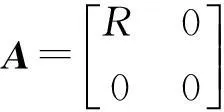
(3)

式中,R=diagram(σ1,σ2,…,σr),其对角元素即为矩阵A的奇异值,将其按照降序排列,即σ1≥σ2≥…≥σr。如果将这些非零奇异值组成一个特征向量x=(σ1,σ2,…,σr)由矩阵奇异值的性质可知,这个特征向量唯一表征了小波包系数矩阵的特征。小波包系数矩阵可反映信号的本质和特征,而特征向量又唯一表征了小波包系数矩阵的特征,所以该特征向量可用于音频信号的表征。

由上文分析可知,奇异值中含音频信号的特征,而奇异值的差异反映的不同频带间的不同特征。为了定量描述这种变化程度,根据信息熵的定义来构造奇异值熵。每个小波系数具有不同的频率成分,且奇异值也不同,对每个分量归一化,得到

(4)

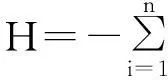
(5)

1.3计算音频信号样本熵

首先对音频信号加滑动时间窗,以0.37s长度为滑动时间窗,计算音频的样本熵,窗口每次移动一个采样点,并计算下0.37s时间窗的音频信号的样本熵,直到计算出最后一次时间窗的音频信号的样本熵为止,从而获得该样本数据中音频信号样本熵的时间序列x={x(1),x(2),…,x(N)},其样本熵的计算步骤为[8]:

(1)给定模式维数m,由原序列组成m维矢量

X(i)={x(i),x(i+1),…,x(i+m-1)}

(6)

式中,i=0,1,2,…,N-m+1;

(2)定义x(i)与x(j)之间的距离

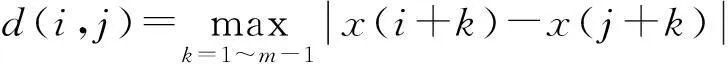
(7)

式中,k=0,1,2,…,m-1;

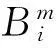
(8)

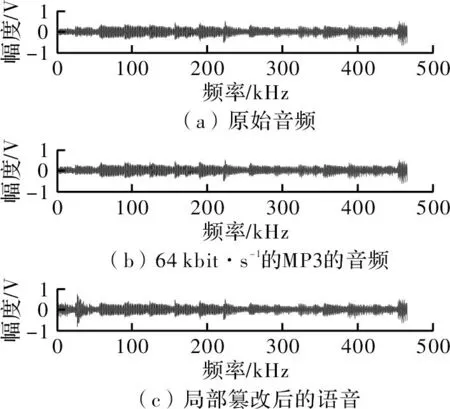
式中,L[d(i,j)

(9)

(4)再对m+1重复步骤(1)～步骤(3),得到Bm+1(r);

(5)理论上,此序列的样本熵为

(10)

当N取有限值时,可得到序列长度为N时的样本熵估计值为

(11)

式中的参数m,r和N参照文献[9],本文选取m=2,r=0.2SD,N=1 024,SD为原始数据的标准差。

2音频指纹提取算法流程

从上述理论分析可看出,各小波包系数的奇异值中包含较全面的音频信号特征,而奇异值的差异反映了音频不同频带间的不同特征,即使相似音频的奇异值熵差别也较大,具有良好的区分度。而样本熵分析方法只需较短数据便可得到稳定的估计值,可表示信号的复杂度和不规则性,具有较好的抗噪能力和抗干扰能力。为此,基于小波包变换将奇异值熵与样本熵相结合来提取音频指纹能全面反映待测音频的特征信息。

本文的音频指纹提取算法如图2所示,主要步骤如下:

图2　音频指纹提取流程

(1)对音频信号进行预处理。将音频转换为16bit/Sample,采样率44.1kHz的单声道信号;

(2)计算样本熵,对音频信号加滑动时间窗,以0.37s长度为滑动时间窗,窗口每次移动得到一个采样点,对所有采样点按式(11)计算样本熵,SampEn0,SampEn1,…,SampEnn;

(3)分帧、加窗与交叠,实验中帧长取2 048,每帧采用汉宁窗平滑帧边缘,交叠因子为P=28/32,汉宁窗公式如下

(12)

(4)采用小波基db4对每一帧音频信号进行5层小波包分解,分别提取第5层从低频到高频各频带成份的小波包分解系数,按照式(2)对所有已得小波包系数进行重构,得到小波包特征矩阵A;

(5)计算奇异值熵,对特征矩阵A进行奇异值分解,得到该矩阵奇异值构成的特征向量σ=(σ0,σ1,…,σn),进而按式(5)计算得到奇异值熵;

(6)将每小波包特征矩阵的奇异值熵与样本熵相结合作为本文音频指纹提取的特征向量,得[SampEn(σ1),SampEn(σ2),…,SampEn(σn)];

(7)提取哈希值,生成音频指纹。统计量的计算是用来提取相关特征值的有效方法。本算法计算以下3个熵统计值

(13)

式中,SampEn(σn)是第k帧i子空间第n个小波包系数的奇异值熵与样本熵相结合的值,Hi表示第k帧i子空间的熵值,HSUMk表示第k帧信号的熵值,Havg表示音乐信号所有帧的平均熵值。

将上述所有帧HSUMk分别与Havg比较,按式(14)每帧产生1位Hash比特值,将所有Hash比特值连接起来即构成该音乐的指纹。

(14)

3实验结果和分析

本文提出的算法性能测试基于Matlab 7.10来实现[10],对待测音频的攻击和编辑使用攻击软件工具StirMark for Audio v0.2完成。实验主要用于验证使用本算法生成的音乐指纹对于常见的音频信号处理是否具有鲁棒性,同时验证不同音乐指纹之间的可区别性。

误码率[11](Bit Error Rate,BER)是数字指纹评价中的一个重要指标,本文采用BER作为未知音乐指纹和原始音乐指纹间的相似性度量标准。设被测指纹和原始指纹的长度为Bbit,不匹配比特位数为n,则BER按式(15)计算

(15)

式中,h′(n)为被测指纹Hash值,h(n)为原始音乐指纹Hash值。

3.1音频指纹鲁棒性测试

鲁棒性测试时验证音频指纹强壮性和实用性的有力指标。本实验随机选取了一段约10.5s的POP风格的音乐片段进行实验。对该音乐先后进行不同的攻击测试:MP3、WMA、RM编码,重采样(将音频信号由原来44 100Hz采样频率变为88 200Hz,然后利用抽取技术还原为原来的采样频率44 100Hz),添加回声,滤波及添加高斯噪声等,提取指纹并分别与原始指纹进行比较,输出误码率作为音乐指纹鲁棒性的判断依据。鲁棒性测试结果如表1所示。

实验数据显示,对于以上常见的音频信号处理,本文算法提取的音频指纹误码率略优于文献[5]算法,其大多数的误码率在0～0.05之间,所有的误码率均低于0.11。尤其是对于现在互联网常用的编码,例如MP3、WMA和RM,在高压缩率下仍能保持低于0.06的误码率,达到了较高的鲁棒性。借鉴Philips研究所的文献[12]中提出的误码率阈值的取值为0.25,若BER低于这个闭值,则认为未知音频片段来源于数据库中被检索出的音频。因此,可认为本算法在经过上述音频处理后提取的指纹具有较高的鲁棒性。

表1　鲁棒性测试结果(BER)

3.2不同歌曲的音频指纹距离实验

音频指纹距离是区分不同音频的重要指标。若不同的音乐片段间具有相似的音频指纹,则会在进行音频指纹检索时引起较高的误码,本实验测试选用5种不同风格的音乐测定不同歌曲间的指纹是否具有足够大的距离,用BER表示的测试结果如表2所示。

实验结果显示,BER越大,不同音乐之间的区别越大,检索结果越准确。由表2明显看出本算法不管是同类或不同类风格的歌曲之间指纹比对的误码率介于0.64~0.794 5之间,多数约在0.70,远超出文献[12]中提出的>0.35的阈值目标,指纹之间具有较大差别,不容易引起误判,这说明该算法在不同歌曲间具有很强的可区分性。

表2　不同歌曲间的音频指纹距离

3.3局部篡改下的指纹性能测试

目前,音频指纹经常会被应用于准确地定位到音频中被局部篡改的帧。由于恶意篡改操作通常对音频的局部进行修改。 由于音频指纹本身是离散的Hash值,因此仅凭BER值无法定位到被篡改音频的位置,还需要通过时间轴上的信号比对来进行判断。若信号的改变是局部的,则可判定是恶意篡改;若信号的变化分布在整个时间轴上,则可认为是正常处理音频的操作,如MP3压缩等,如图3所示。

图3　MP3处理和恶意篡改的信号在时间轴上的区别

将1.035～2.035s的音频用任意1s的音频替换后,算法检测发现24~45共计22个帧的检测错误,说明算法能够较准确地定位到相应被替换的帧。

4结束语

本文提出了一种改进的基于小波包变换的音频指纹提取算法。实验结果表明,该算法提取的音频指纹具有良好的区分度,对常见音频处理具有较高的鲁棒性,尤其是处理非平稳性较强的音频,其鲁棒性和音频

区分能力明显优于Philips算法及其改进算法,同时也具有较强的识别音频篡改能力。

本文算法的优点在于在小波包变换的基础上将数学理论中的奇异值熵和样本熵引入音频指纹提取技术中,充分反映了音频不同频带间的不同特征。下一步工作将着重研究将音频的特征集中到更少的小波包系数上,进一步提高音频指纹的提取时间。

参考文献

[1]李伟,李晓强,陈芳,等.数字音频指纹技术综述[J].小型微型计算机系统,2008,29(11):2124-2130.

[2]SukittanonS,AtlasLE.Modulationfrequencyfeaturesforaudiofingerprinting[C].Shanghai:InternationalConferenceonAcoustic,SpeechandSignalProcessing(ICASSP2002),2002.

[3]SukittanonS,AtlasLE,PittonJW.Modulation-scaleanalysisforcontentidentification[J].IEEETransactionsonSignalProcessing,2004,52(10):3023-3035.

[4]OzerH,SankurB,AnarimE.Perceptualaudiohashingfunctions[J].EURASIPJournalonAppliedSignalProcessing,2005(12):1780-1793.

[5]陈芳,李伟,李晓强.基于小波包最优基的音乐指纹提取算法[J].计算机工程,2009,35(9):236-240.

[6]王松岭,刘锦廉,许小刚.基于小波包变换和奇异值分解的风机故障诊断研究[J].热力发电,2013,42(11):101-106.

[7]陈桂明,杨斌,何庆飞.一种基于奇异值的小波包改进算法[J].噪声与振动控制,2013(1):59-63,67.

[8]周鹏,葛家怡,曹红宝.基于样本熵的运动想象分类研究[J].信息与控制,2008,37(2):191-196.

[9]张毅,冯晓林,罗元.基于改进小波包与样本熵的表面肌电信号特征提取[J].计算机应用研究,2015,32(3):701-704.

[10]胡昌华,李国华,刘涛,等.Matlab6.X的系统分析与设计-小波分析[M].西安:西安电子科技大学出版社,2004.

[11]明建成,韩威.基于音频指纹的压缩域音频识别方法研究[J].科学技术与工程,2014,14(16):1671-1815.

[12]CottonCV,EllisDPW.Audiofingerprintingtoidentifymultiplevideosofanevent[C].Lanzhou:IEEEInternationalConferenceonAcousticsSpeechandSignalProcessingICASSP,2010.

中图分类号TP391

文献标识码A

文章编号1007-7820(2016)03-030-05

doi:10.16180/j.cnki.issn1007-7820.2016.03.008

作者简介:朱洁(1991—),女,硕士研究生。研究方向:音频指纹技术等。邓开发(1965—),男,博士,教授,硕士生导师。研究方向:光信息与计算机处理等。

基金项目:南京市领军型科技创业人才引进计划基金资助项目(2014A090002)

收稿日期:2015- 07- 20