两种针对小信号的脉压优化算法及实现

卢文良

(海军701工厂 研发部,北京　100015)



两种针对小信号的脉压优化算法及实现

卢文良

(海军701工厂 研发部,北京100015)

摘要结合某雷达项目,针对项目LFM和Taylor编码两种小时宽带宽积(TB)信号脉冲压缩效果不理想的问题,通过对两种不同小TB信号的实际回波波形和特性进行了分析,针对性地使用了倒推法和循环迭代法,获得了优化的脉压系数。试验得出结论,较之传统的匹配滤波脉冲压缩系数,采用优化脉压系数的LFM和Taylor编码小TB信号脉冲压缩主副瓣比均能提高十几dB。

关键词脉冲压缩;倒推法;循环迭代法

Two Small Signal Pulse Compression Algorithms and Their Implementation

LU Wenliang

(R & D Department,Navy 701 Factory,Beijing 100015,China)

AbstractBased on a radar project,in which the result of two small TB signal (the LFM and Taylor) pulse compression methods are not good enough,the article firstly analyses the shape and characteristics of the two small TB signal.The optimum compressed coefficient is obtained by the reverse algorithm and the circulation algorithm respectively.Experiments show that the main lobe to sidelobe ratio can be improved by more than 10 dB compared with that by the traditional compression algorithms.

Keywordspulse compression;reverse algorithm;circulation algorithm

众所周知,脉冲压缩体制的雷达可在发射时采用宽脉冲保证足够的作用距离,接收时通过脉冲压缩获得窄脉冲,将目标信息从杂波背景中提取出来,因而能较好地解决作用距离和分辨能力之间的矛盾[1]。随着高速大规模集成电路的发展,数字脉冲压缩系统受到了广泛的重视并普遍应用于各种雷达设计中。它利用一组匹配滤波脉压系数模拟脉冲压缩系统,并通过对脉压系数进行一系列变换来改进脉冲压缩的性能,提高脉冲压缩的主副瓣比。可对于小时宽带宽积信号而言,即便进行加窗脉冲压缩,得到的主副瓣比仍较小,小目标不易被检测出来。且在实际处理过程中,由于回波与发射信号不能够完全匹配、雷达噪声影响较大等因素,进一步降低了小时宽带宽积信号脉冲压缩的主副瓣比,加大了雷达检测小目标的困难程度。因此常常会出现通过理论计算和计算机仿真设定的脉冲压缩技术指标与实际应用结果相差甚远,不容易满足要求的情况出现。为解决这个问题,提高雷达检测性能,人们进行了诸多努力[2-6]。

结合某雷达项目,针对信号处理中LFM和Taylor编码小时宽带宽积信号脉冲压缩效果不理想的问题,本文提出了使用倒推法和循环迭代法分别对两种小时宽带宽积信号产生优化的脉冲压缩系数,以提高脉冲压缩的主副瓣比。通过大量试验,表明倒推法对于LFM信号效果较好,循环迭代法则对Taylor编码信号效果显著。本文介绍了算法的硬件实现和使用方法,即采用FPGA+DSP芯片组合方式的信号处理板,具有并行、高速、大容量、高可靠性的优点。由FPGA芯片进行下变频获得基带信号作为算法输入,根据相应算法得到优化的脉压系数,再将脉压系数存储到DSP芯片中进行脉压运算。最后将两种脉压算法的脉压结果表示出来,大量试验表明这两种算法较传统匹配滤波脉压算法主副瓣比性能有大幅提高。目前上述两种算法已成功得到应用。

1背景介绍

理想情况下的脉冲压缩系统是一个匹配滤波系统,其要求其相频特性与发射信号实现相位共轭匹配[7]。

假设输入信号为ui(t),其频域表达式为式(1)所示

(1)

若使用传统数字频域脉压,脉压系数应为输入信号频谱的共轭转置,即如式(2)所示

(2)

通常会对脉压系数在时域或频域加窗来提高脉压性能。以LFM小时宽带宽积信号为例,加窗后脉冲压缩的主副瓣比较之加窗前有较大提高,仿真证明,时域加窗结果比频域加窗结果效果更为显著。在此选择时域加窗,则时域加窗可表示为

h(t)=ui(t)×hamming(t)

(3)

hamming(t)为汉明窗函数。

将h(t)变换到频域可表示为

(4)

频域加窗系数为输入信号频谱的共轭转置,即

(5)

频域脉压输出为

Uo(ω)=Ui(ω)Hhamming(ω)

(6)

可得匹配滤波脉冲压缩结果为

uo(t)=ifft[Uo(ω)]

(7)

由于匹配滤波脉冲压缩将信号能量集中于一点,而随机噪声能量维持不变,所以能提高输出信号信噪比,将信号从噪声中分离出来。脉冲压缩输出信号的信噪比与输入信号信噪比之比提高了D倍,D等于时宽带宽积,即

(8)

由此可看出,在相同输入信号条件下,大时宽带宽积信号较之小时宽带宽积信号有更好的脉压性能,更易被检测出来。

必须指出在实际实现时通常不可能得到完全匹配,迫使系统工作在一定程度的“失配”状态下,所得脉冲压缩性能要远低于式(8)的结论。因此对于小时宽带宽积信号来说,如何提高脉压性能,达到实际需求就显得尤为重要。

本项目中用到两种信号形式:LFM信号和Taylor四相编码信号。

LFM信号的数学表达式[8]为

(9)

其中,τ为信号时宽;μ为信号的调频斜率;ω0为信号中心频率;A为信号幅度。

Taylor编码信号的一般表达式为

(10)

其中,vk代表第k位Taylor编码,其含义为

vk=js(k-1)Wk

(11)

式中,s是固定值,值为+1或-1;Wk表示第k位二相码,是+1(0°)或-1(180°)。

式(10)中,p(t)是周期为4T的半余弦波形

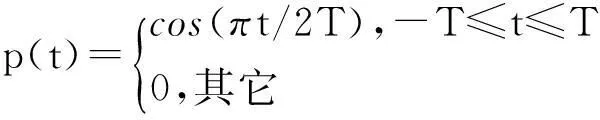
(12)

这里T为子脉冲宽度。

2改进方法

2.1倒推法

倒推法通过提取匹配滤波脉冲压缩输出信号的相位和幅度信息,合成理想的脉冲压缩结果,并对脉冲压缩过程做逆变换,获得优化的脉冲压缩系数。

由前面脉冲压缩的基本原理和推导公式可知,脉冲压缩的输出可表示如式(7)所示,其最大值可以表示为

(13)

表征脉冲压缩性能的主要指标主副瓣比通过下式表征

(14)

为获得理想脉冲压缩结果的理想波形,首先选择输出信号主副瓣比波形中信号主瓣以外的区域,乘以一个主副瓣比降低因子N,将副瓣和噪声区域的分贝值大幅降低,如下式所示

sdbdream(t)=sdb×N

(15)

结合式(14)和式(15)推导得到uabs(t)的表达式为

(16)

脉冲压缩输出信号uo(t)的相位可表示为

α(t)=angle(uo(t))

(17)

则理想脉冲压缩的输出信号udream(t)可表示为

udream(t)=uabs(t)ejα(t)/π

(18)

将其变换到频域,理想脉冲压缩结果为

Udream(ω)=fft(udream(t))

(19)

可得脉压系数的频域表达形式为

(20)

使用式(20)得到的理想频域脉压系数Hdream(ω)进行脉冲压缩可提高输出信号的主副瓣比十几dB。通过改变N的大小,可相应改善脉冲压缩主副瓣比的大小,但N达到一定值后,改善作用便不能提高,这与实际信号的相关性和信号纯净度有关。

2.2循环迭代法

循环迭代法以脉冲压缩输出信号的积分副瓣电平为指标,通过对脉冲压缩过程的不断循环迭代,最终获得积分副瓣电平最小时的脉冲压缩系数。

假设长度为N的Taylor信号第k个采样点可表示为sk,k=0…N-1。将信号{sk}拓展,得到长度为P(P≥N)的脉冲压缩输入信号

S=sT=[0…0s0s1…sN-10…0]

(21)

假设脉冲压缩数字滤波器系数可表示为

hT=[h0h1…hN-1hN…hp-1]

(22)

信号通过脉冲压缩数字滤波器后输出可表示为

y=hHX

(23)

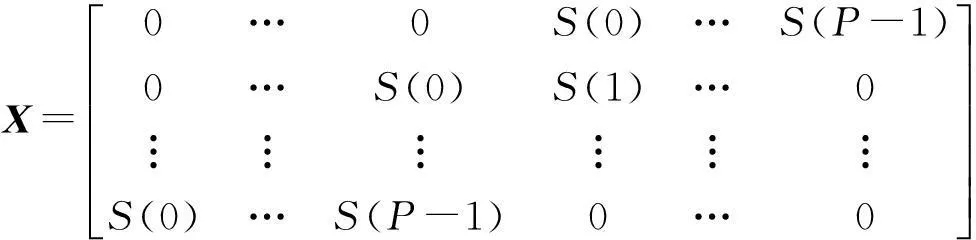
(24)

为增大脉冲压缩输出信号的主副瓣比,采用积分副电平(ISL)作为循环收敛的指标,如下式所示

ISL=yHWy

(25)

W=diag(w1…wp-1wp…w2p-1)=diag(1…101…1)

(26)

同时满足在主瓣方向的输出为一常数,即

(27)

求解,得

h=B-1S(SHBS)-1N

(28)

其中,B=XWXH。由于(SHBS)-1N为一常数,从而

h=B-1S

(29)

式(27)是针对积分副瓣电平而言,实际希望输出峰值副瓣电平最小,这可调整式(26)中权矢量的构成,对高副瓣赋以大的权值。调整公式为

(30)

通过调整加权系数矩阵W以及脉冲压缩数字滤波器阶数P,采用循环迭代算法便可得到较为满意的滤波器设计结果,其过程如图1所示。

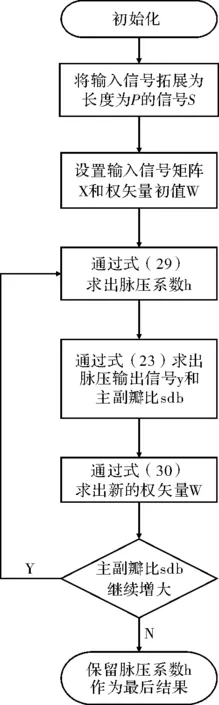
图1　循环迭代法流程图

3硬件实现

上述两种脉压系数产生算法由包含FPGA+DSP芯片组合的信号处理板来实现,FPGA采用Altera公司的CycloneⅡ系列的EP2C484C6芯片[9],完成下变频功能,DSP采用AD公司的TS201芯片,进行脉冲压缩运算,FPGA和DSP之间采用Link口通信。整个系统具有大存储量、大运算量和并行处理的能力,支持高速I/O和级联特性,其处理板结构图如图2所示。算法实现方法如下:

首先信号处理板接收频综产生的中频输入信号,通过A/D变换后,进入FPGA芯片实现下变频,将中频信号转换为基带信号,并经过抽取,通过Link口进入DSP芯片,DSP芯片将采到的基带信号导出,作为上述两种算法的输入信号。计算机使用Matlab对两种算法进行编程,并使用基带信号产生我们所需要的优化脉压系数。将产生的脉压系数烧入DSP芯片内作为脉压系数存储,重新运行脉冲压缩程序,此时信号处理板就能够得到更好的脉冲压缩主副瓣比,脉压结果可导出至Matlab进行观察和比较。

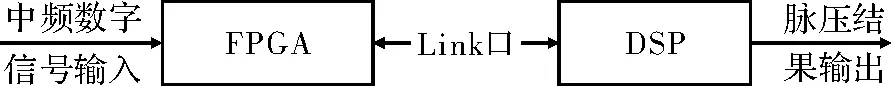
图2信号处理板结构图

4实验结果

图3是采集到的解调后实际LFM小时宽带宽积回波信号波形,时宽为20μs,带宽2MHz,采样频率8MHz。图4是采集到的解调后Taylor编码小时宽带宽积回波实、虚部信号波形,其子脉冲时宽为0.5μs,码元个数为40,采样频率为4MHz。可以看到,LFM和Taylor信号的波形均已发生形变,与计算机仿真波形相差甚远。

图3　LFM小信号实际波形图

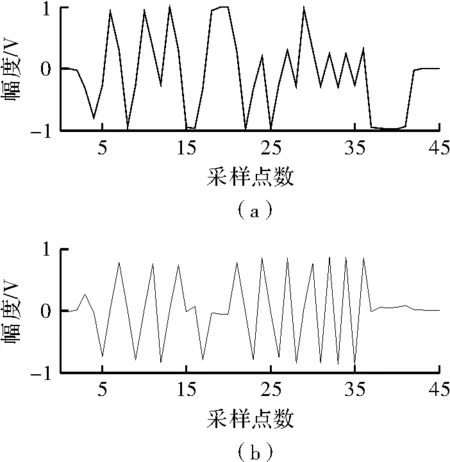
图4　Taylor小信号波形图

下面是与匹配滤波加权(Hamming)法进行比较的结果图,由于传统的不加权匹配滤波法脉压结果只有约10dB,本文为了比较结果清晰,不将不加权匹配滤波结果表示在图上。

图5表示对LFM小时宽带宽积实际信号分别用匹配滤波加权法和倒推法进行脉压的结果,可以看到,匹配滤波加权算法的脉压主副瓣比为22dB,在主副瓣比增加因子N=4的情况下,倒推法的脉压主副瓣比为36dB,较匹配滤波提高了14dB。

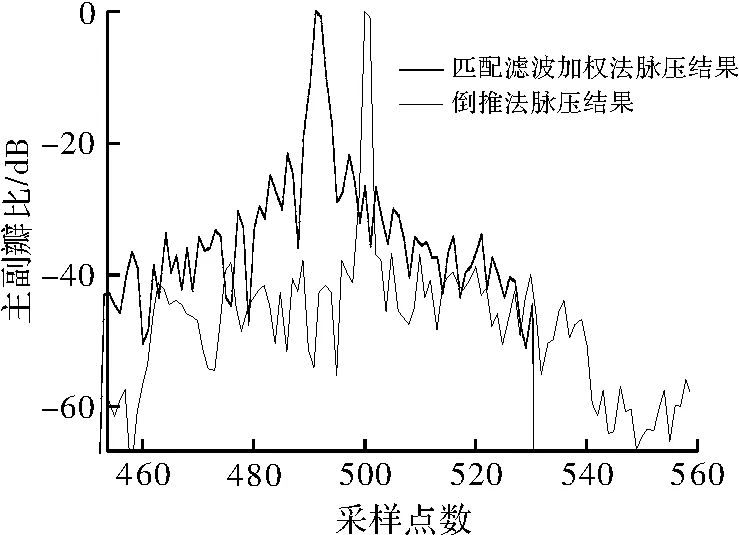
图5　 LFM信号匹配滤波加权法与倒推法脉压结果的比较

图6表示对Taylor小时宽带宽积实际信号分别用匹配滤波加权法和循环迭代法进行脉压的结果,可以看到,匹配滤波加权的脉压主副瓣比为17dB,在脉冲压缩系数长度P=300的情况下,倒推法的脉压主副瓣比为34dB,较匹配滤波提高了17dB。

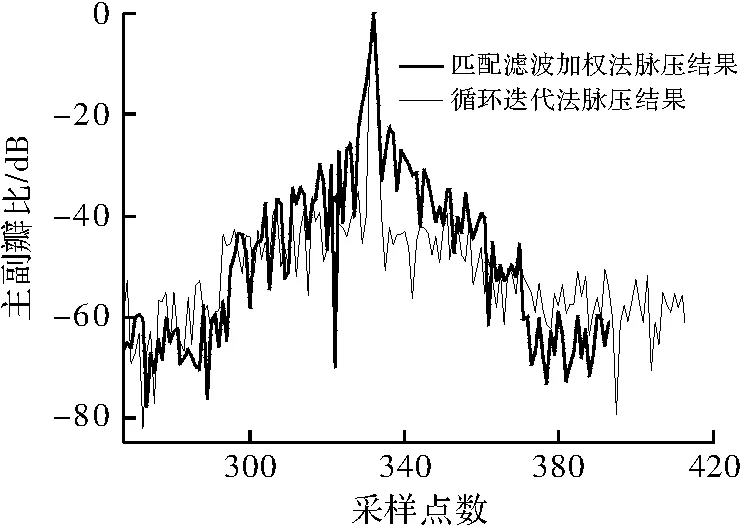
图6　Taylor信号匹配滤波加权法与循环迭代法脉压结果的比较

从实验结果可知,这两种算法较传统匹配滤波较算法对于提高小时宽带宽积信号的主副瓣比有较大提高,但是这两种方法会受到不同信号质量的影响,主副瓣比的提高有限。

5结束语

在雷达信号处理中,对小时宽带宽积信号进行匹配滤波脉冲压缩的结果主副瓣比通常不够理想,本文针对LFM和Taylor两种小时宽带宽积信号采用了不同的优化算法,试验证明这两种算法可以将脉冲压缩的主副瓣比提高十几dB,大幅提高了雷达的探测能力。除了算法原理,本文还介绍了算法实现的硬件平台,即一个由FPGA和DSP芯片组成的高速、大容量、高速I/O信号处理板,能满足优化脉压系数的产生和应用。无论是对于倒推法或循环迭代法而言,基带信号的纯净度和参数的选择对脉冲压缩的性能有较大影响,需要考虑到波形完整性、噪声大小、运算量、主瓣宽度和旁瓣长度等因素。

参考文献

[1]MerrillISkolnik.Radarhandbook[M].3版.北京:电子工业出版社,2010.

[2]陶广源,廖桂生,刘宏伟.多相码信号数字脉压滤波器设计[J].电波科学学报,2003,18(2):143-146,152.

[3]王萱芬,李巍,王子立.一种实现超低旁瓣的脉冲压缩算法[J].现代电子技术,2009,32(23):5-7.

[4]王丽萍,苏涛.一种迭代加权最小二乘旁瓣抑制滤波器设计[J].火控雷达技术,2008,37(1):92-96.

[5]徐景明,朱灿焰.一种复合调制信号的脉冲压缩及DSP实现[J].雷达科学与技术,2010,8(5):448-451.

[6]张宏伟,任新涛,汤宫民,等.编码信号的脉冲压缩技术及实现[J].计算机测量与控制,2012,20(12):3348-3350.

[7]丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社,2001.

[8]向敬成,张明友.雷达系统[M].北京:电子工业出版社,2001.

[9]AlteraCorporation.CycloneⅡdevicehand-book[M].MAUSA:AlteraCorporation,2005.

中图分类号TN957.51

文献标识码A

文章编号1007-7820(2016)03-061-04

doi:10.16180/j.cnki.issn1007-7820.2016.03.015

作者简介:卢文良(1981—),男,工程师。研究方向:雷达信号处理。

收稿日期:2015- 07- 23