导航卫星接收机窄带干扰抑制算法研究

赵月露,纪　磊

(1.西安电子科技大学 电子工程学院,陕西 西安　710071;2.北京理工大学 生命学院,北京　100021)



导航卫星接收机窄带干扰抑制算法研究

赵月露1,纪磊2

(1.西安电子科技大学 电子工程学院,陕西 西安710071;2.北京理工大学 生命学院,北京100021)

摘要在GNSS服务过程中,地面接收到的卫星导航信号的功率较小,且易受到周围复杂电磁干扰影响,这将会导致卫星无法正常定位。针对常见的窄带干扰,介绍一种新型自适应全通IIR陷波器,自适应算法采用高斯-牛顿迭代法,通过跟踪窄带干扰频点,对其频点进行陷波。文中在其基础上进行改进,在每次迭代过程中采用最佳收敛因子,最大程度地减少均方误差。这种算法可导致更快的收敛速度和更高的估计精度。仿真结果表明,IIR滤波器可有效去除高达70 dB的窄带干扰。

关键词窄带干扰;IIR滤波器;高斯-牛顿算法;最佳收敛因子

Research on Narrowband Interference Suppression Algorithm for Satellite Navigation Receiver

ZHAO Yuelu1,JI Lei2

(1.School of Electronic Engineering,Xidian University,Xi’an 710071,China;

2.School of Life Science,Beijing Institute of Technology,Beijing 100021,China)

AbstractIn GNSS service process,the power of the satellite navigation signal received on the ground is very small and easily affected by surrounding complex electromagnetic interference,which can lead to failure in satellite positioning.e.A new adaptive all-pass notch filter based on the Gauss-Newton algorithm by which the frequency points are trapped by tracking narrow-band interference frequency points is introduced for the common narrowband interference.This algorithm is improved by using the best convergence factor in each iteration to reduce the mean square error.This improved algorithm enjoys a faster convergence speed and higher estimation precision.The simulation results show that the IIR filter can effectively remove up to 70 dB narrow-band interference.

Keywordsnarrowband interference;IIR filter;Gauss-Newton algorithm;the optimal convergence factor

全球导航卫星系统(Global Navigation Satellite System,GNSS)广泛应用于定位导航、授时校频、精密测量等,成为人类从事政治、科学、经济和军事活动必不可少的信息技术。卫星导航接收机的捕获、跟踪、定位等工作依赖于外部的射频信号,因而易受到外来射频干扰的影响[1]。目前将所面临的干扰分为两类:一是复杂的认为电磁环境产生的干扰,包括无意干扰和有意干扰;二是复杂的自然电磁环境产生的干扰[2-3]。通常所说的窄带干扰是指所占频带远远小于扩频信号带宽的干扰信号。窄带干扰的抑制可通过在时域或频域进行,在频域进行陷波抑制要采用先接收、后处理的方式,而在时域中可同时接收、同时处理的方式,因此时域陷波的实时性要比频域好。时域窄带干扰抑制技术是将已经锁定的信号与外来干扰信号进行比对,利用窄带干扰信号与卫星信号相关性不强的特点来实现滤波,主要方法是时域滤波器。由于IIR滤波器实现所需阶数低,硬件实现代价小,本文介绍了一种新的自适应全通陷波器(Adaptive All-Pass Based Notch Filter,ANFA)[4],采用高斯-牛顿(MAGN)算法进行收敛。这种基于高斯-牛顿算法的全通陷波器比传统的线性预测器在信噪比改善和干扰环境下平均功率(Mean Output Power,MOP)方面有更好的效果。

1自适应全通陷波器

1.1全通陷波器原理

自适应陷波器(Adaptive Notch Filter,ANF)被广泛应用于诸多信号处理中,消除或跟踪窄带干扰。陷波器的基本原理即在干扰的频率处产生零陷,保持其他频点处增益不变,其理想传递函数为

(1)

式(1)中,ω=ω1,ω2,…,ωM为M个干扰频点。基于全通陷波器的传递函数可表示为[5]

(2)

其结构如图1所示。

图1　全通陷波器结构图

采用该结构的优点是全通滤波器的分子分母具有镜像对称的关系,这样可降低陷波器系数的敏感度,从而增加陷波器的稳定性,该陷波器属于的IIR滤波器,相比有相同系数的FIR滤波器,IIR滤波器有更好的性能。

二阶全通陷波器[5]可写为

(3)

同理,2P阶全通陷波器的传递函数为

(4)

其中,βi=-2cos(ωp,i),p是陷波数;ωp,i为第i个极角。为得到约束陷波滤波器(Constrained Notch Filter,CNF)的系数和特征,必须对约束陷波器和陷波滤波器进行分析和比较。2P阶陷波滤波器加一般约束形式表示为

(5)

其中,ri=-2cos(ωi),ωi表示第i个陷波频率,设T(z)和TCNF(z)是具有有限多分子分母的多项式,NFA和相应系数的传递函数T(z)可导出并配置成

(6)

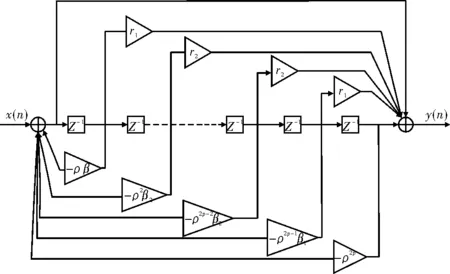
图2　全通陷波器模型结构

1.2改进的高斯-牛顿算法

(1)高斯-牛顿自适应算法。高斯-牛顿算法[5]的基本思想就是把非线性最小二乘问题转化为一些列的线性最小二乘法问题来迭代求解,在每次迭代的过程中,计算出最优的收敛因子,并运用到高斯-牛顿算法系数更新的迭代公式中,加快收敛速度,使输出信号的功率达到最小值,从而达到抑制干扰的目的。高斯-牛顿算法属于梯度法,即一种梯度导向的启发式搜索算法,目标函数的最小化利用逆Hessian矩阵和梯度向量的估计值在牛顿方向上搜索得到。

滤波器参数矢量θ(n)被定义为θ(n)=[r1(n)r2(n)…rp(n)]T,均方误差定义为

ξ=E[e2(n)]=E[(d(n)-y(n))2]

(7)

在此定义梯度为

(8)

根据Hessian矩阵定义,对误差向量求2次偏导数

(9)

则Hessian可近似为梯度向量的加权和,形式如下

(10)

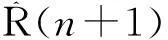
(11)

此处α遗忘因子,α越趋近于0,说明过去的信息对现在影响越大,反之则越小。α值通常在0~0.1之间选取。

由以上公式推导得系数向量的更新公式为

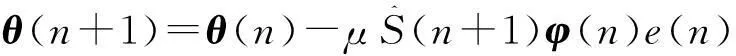
(12)

此处μ称为收敛因子,主要用于控制自适应滤波器的稳定性以及收敛性,一般采用固定值,本文介绍了一种实时更新收敛因子,使收敛因子最终达到最优值。

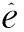
目标函数的最小均方误差估计值为

(13)

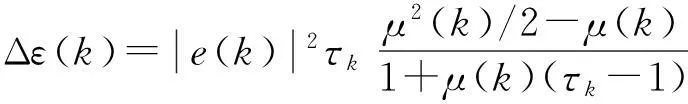
(14)

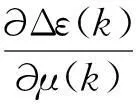
2仿真分析

为进一步说明此算法的功能及性能,通过自己建立信号模型,使用Matlab自适应4阶陷波器进行仿真分析。

采用输入信号x(n)=golden(n)cos(2πfc)+Acos(2πfin)+n(n),式中golden(n)cos(2πfc)是有用信号,其由GNSS中Gloden码形成,频宽为20 MHz,载频fc为15.48 MHz;n(n)为服从(0,1)的高斯白噪声;Acos(2πfin)为窄带干扰信号,采样频率为fs为62 MHz,干扰频点为8 MHz、10 MHz,信噪比为-20 dB。

(1)两个单音干扰。图3为干信比50 dB的两个单音干扰仿真对比图,图3(a)中,单音干扰频点为8 MHz、10 MHz。从图3(b)中可明显看到,8 MHz和10 MHz处的干扰频点被滤除掉。从图3(d)中,可看到去除干扰后幅度明显降低。通过仿真证明,此算法可滤除干信比高达80 dB的单音干扰。图4为IIR滤波器的幅频和相频响应图。

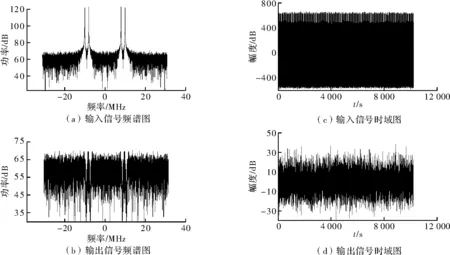
图3　IIR陷波器滤波前后时频域对比图

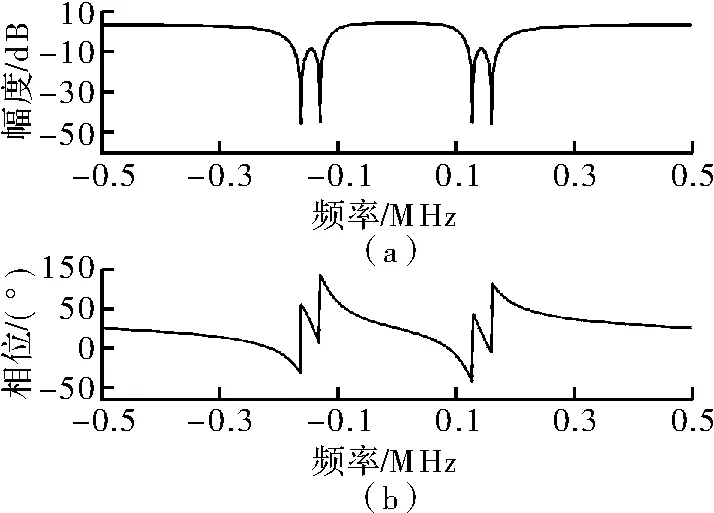
图4　IIR陷波器幅频响应和相频响应图

导航系统中,信号的同步过程是将接收机接收到的信号与本地的测距码进行自相关运算,当信号的测距码相位和本地的测距码相位对齐时,会产生一个最大值,从而成功捕获到导航信号[9]。图5是单音干扰下输出信号与本地测距码的互相关值,由图5可知,将经过抗干扰算法的信号与本地测距码做相关运算捕获,产生了一个明显的峰值,表明可成功的捕获到导航信号。

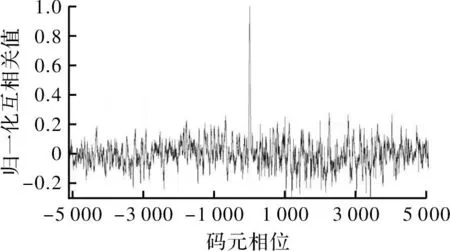
图5　单音干扰下输出信号与本地测距码的互相关值

(2)两个窄带干扰。图6是干信比为40dB的两个窄带干扰的仿真对比图,窄带干扰的带宽为导航信号的10%。图6(a)中,干扰中心频点为8MHz、10MHz,窄带带宽为有效信号的1/10。从图6(b)中可明显看到,8MHz和10MHz处的干扰频点被滤除掉。图6(d)为滤波后输出信号的时域图,可看到去除干扰后幅度明显降低。通过仿真,此算法可滤除干信比达60dB的窄带干扰,窄带干扰过大,滤波效果将有所降低。

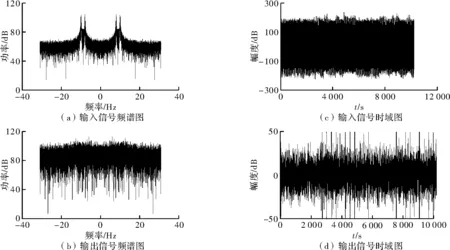
图6　窄带干扰滤波前后时频域对比图

图7为IIR陷波器的幅频响应和相频响应图,可看到分别在两个窄带干扰中心频点处有一个陷波,用于将此干扰频点的信号滤除。

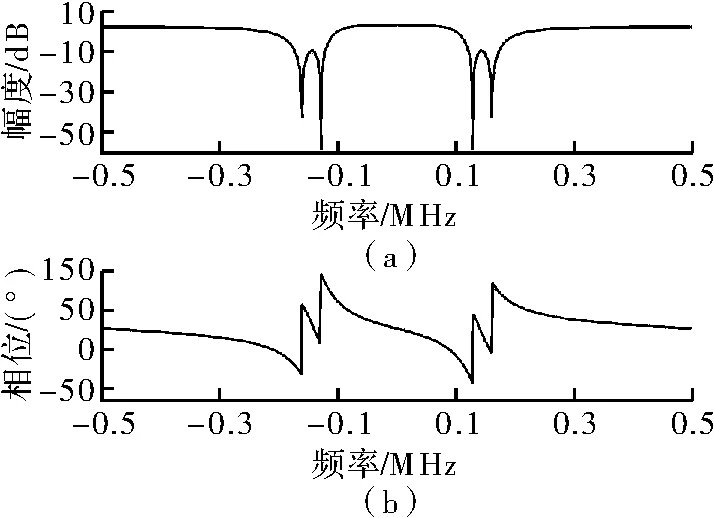
图7　IIR陷波器的幅频响应和相频响应图

图8是窄带干扰下输出信号与本地测距码的互相关值,由图可知,将经过抗干扰算法的信号与本地测距码做相关运算捕获,产生了一个明显的峰值,表明可成功的捕获到导航信号。

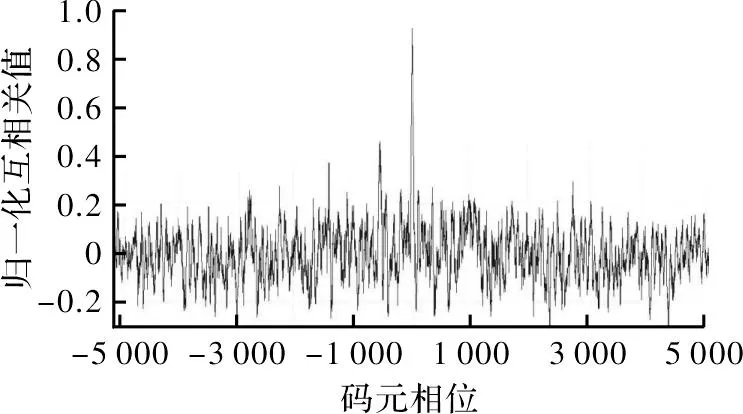
图8　窄带干扰下输出信号与本地测距码的互相关值

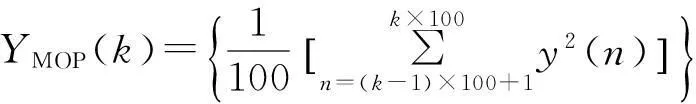
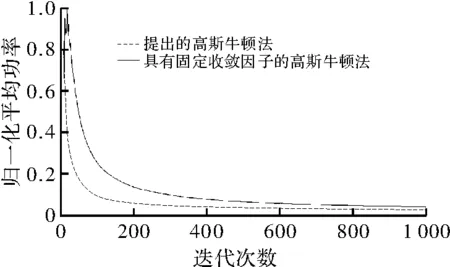
图9　收敛速度对比

3结束语

现代导航信号受到各种各样的导航干扰的影响,大幅降低了导航性能,以窄带干扰最为常见,其中单音干扰对信号的影响尤其明显。实际应用中可通过时域抗窄带干扰接收对信号进行预处理,增强系统的抗干扰能力。基于高斯-牛顿的IIR陷波器可用在提高卫星接收机窄带干扰抑制模块中,用以提高接收机的性能。对传统的高斯牛顿算法进行了改进,在每次迭代中采用最佳收敛因子,运用到自适应陷波器中,使陷波器自动调节滤波系数,在干扰频点处陷波,达到抑制干

扰的目的。

参考文献

[1]孟凡科,武拥军.对GPS接收机的干扰信号分析[J].航天电子对抗,2002(4):13-16.

[2]宋颖凤,葛海龙,王四红.对GPS的干扰与抗干扰技术研究[J].舰船电子工程,2004(6):26-30.

[3]杨克元.GPS接收机抗干扰算法及其实现研究[D].成都:电子科技大学,2010.

[4]LiuY,LaaksoTI,DinizPSR.AcomplexadaptiveIIRnotchfilteralgorithmwithopti-malconvergencefactor,ineuropeanconferenceoncircuittheoryanddesign[C].London:EuropeanConferenceonCircuitTheoryandDesign,2001.

[5]SimonHaykin.自适应滤波器原理[M].4版.郑宝玉,译.北京:电子工业出版社,2006.

[6]AryeNehorai.Aminimalparameteradaptivenotchfilterwithconstrainedpolesandzeros[J].IEEETransactionsonAcoustSpeechSignalProcess,1985,33(4):983-996.

[7]CousseauJE,DinizPSR.OnoptimalconvergencefactorforIIRadaptivefilter[C].NewYork:IEEEISCAS’94,1994.

[8]MaoWeilung.Newaadaptiveall-passbasednotchfilterfornarrowbandFManti-jammingGPSreceiver[J].Circuits,SystemsandSignalProcessing,2011,30(6):527-542.

[9]谢刚.GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[10]RuschLA,PoorHV.NarrowbandinterferencesuppressioninCDMAspreadspectrumcommunications[J].IEEETransactionsonCommunication,1994,42(3):1969-1979.

中图分类号TN967.1

文献标识码A

文章编号1007-7820(2016)03-053-05

doi:10.16180/j.cnki.issn1007-7820.2016.03.013

作者简介:赵月露(1989—),女,硕士研究生。研究方向:卫星导航接收机窄带干扰抑制。

收稿日期:2015- 07- 19