基于网络设计的路段可逆车道布局优化

叶静茹,马晓旦,夏晓梅,赵　靖

(上海理工大学 管理学院,上海　200093)



基于网络设计的路段可逆车道布局优化

叶静茹,马晓旦,夏晓梅,赵靖

(上海理工大学 管理学院,上海200093)

摘要为了应对城市道路交通供需关系的变化情况,合理分配道路空间资源,文中对可逆车道布局进行了研究,利用双层规划方法,建立了以系统总出行时间最小为上层问题目标,以非对称影响的SUE问题为下层问题的可逆车道设置位置和规模的优化模型。该模型中,在需求层面,考虑了3种不同出行特性的车辆:社会车辆、公交车辆和紧急救援车辆;在供给层面,模型中将引入对交叉口的考虑,不仅在计算出行时间中考虑交叉口的影响,且在优化变量中将路段可变车道与交叉口车道功能一同考虑。文中给出了模型的求解方法,对于上层问题采用粒子群优化算法求解,对于下层采用结合了MSA算法的"对角化"算法求解。经计算,系统总出行时间降低了20%。证明该可逆车道的设置是合理有效的。

关键词交通工程;可逆车道;双层规划;网络设计

Optimization Layout for Reversible Lane Based on Discrete Network Design

YE Jingru,MA Xiaodan,XIA Xiaomei,ZHAO Jing

(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractAn optimal layout of the reversible lane is proposed to deal with the significant change of the relationship between the supply and demand of the urban road.A bi-level programming model is established in which transportation management section at the upper level disposes the reversible lane to minimize the total system cost while transportation users at the lower level follow stochastic user equilibrium assignment principle to select travel routes.For the traffic demand,three kinds of vehicles with different travel characteristics are considered:social vehicles,buses and emergency vehicles.For the network representation,the intersection is taken into consideration both in calculating the travel time and in optimizing the layout of the reversible lane.A solution algorithm is also developed,in which the upper level problem are solved by the particle swarm optimization approach and the lower level problem are solved by the diagonalization algorithm combined with method of successive averages.The overall travel time of the system is calculated to be reduced by 20%,a proof of the feasibility of the reversible lane design.

Keywordstraffic engineering;reversible lane;bi-level programming;network design

可逆车道是一种经济有效地提升拥挤流向道路通行能力的方法,可使通行能力与交通需求相匹配[1]。选择合适的可逆车道设置位置,是可逆车道规划设计阶段的一项重要内容。

1基于经验的可逆车道实施条件

AASHTO Green Book[2]建议在道路高峰小时交通量方向分布系数≥65%时,可考虑采用可逆车道。ITE[3]指定性的指出设置可逆车道应满足包括流量等4方面条件。MUTCD[4]建议,对于双向道路,当存在周期性的交通拥挤,同时交通量方向分布系数达到66%～75%时,可考虑采用可逆车道。

1.1基于路段/路径考虑的可逆车道设置

Hausknecht[5]分别以路段往返两个方向通行能力最大和总阻抗最小为目标,提出了可逆车道设置的(非)线性规划模型。但可逆车道方案实施,是需要道路网络条件做支持的,若应用不当,结果可能适得其反[6]。

1.2基于路网考虑的可逆车道设置

Liang[7]以路网总阻抗最小为上层优化目标,下层采用随机用户均衡分配模型,采用枚举法进行求解。张好智[8]采用粒子群优化(PSO)算法,给出了上述问题的优化求解算法步骤。

Xie[9]提出一种基于车道的网络疏散优化方法,在该模型中建立双层规划模型,并采用拉格朗日松弛和禁忌搜索的方法对模型进行求解。Karoonsoontawong[10]在Xie的基础上增加了时间因素。该研究采用遗传算法对模型进行求解。

综上所述,本文建立可逆车道设置优化模型。在需求层面,模型从以往一种类型的车辆,拓展到3种不同出行特性的车辆:社会车辆、公交车辆和紧急救援车辆。在供给层面,模型中将引入对交叉口的考虑。

2研究框架

图1说明了本研究的总体分析顺序,文中各参数含义如表1所示。

图1　总体框架

数含义A路网连线集合AI交叉口连线集合AR路段连线集合c1,c2粒子群算法中的加速常数cjs路段连线(j,s)的通行能力,veh/hCI交叉口I的信号周期时长,sd1ij交叉口流向(i,j)的均匀控制延误,sd2ij交叉口流向(i,j)的增量延误,sd3ij交叉口流向(i,j)的初始排队延误延误,sfrskO-D对r-s之间路径k上的流量,veh/hgij交叉口流向(i,j)的有效绿灯时长,sgbestt粒子群中所有粒子中历史最小的适应度IHCM延误模型中上游汇入后限流的修正参数kHCM延误模型中增量延误参数k连接O-D对的路径集合M一个充分大的数ni交叉口岔口i的进出口道总车道数,条ni0交叉口进口i的基本车道数,条nij交叉口连线(i,j)的车道数,条n0ij交叉口连线(i,j)的基本车道数,条nrij交叉口连线(i,j)的可变车道数,条nir交叉口进口i的可变车道数,条njs路段连线(j,s)的车道数,条n0js路段连线(j,s)的基本车道数,条nrjs路段连线(j,s)的可变车道数,条nrEjs路段连线(j,s)上紧急救援对可变车道的需求,条njs,sj路段连线(j,s)和(s,j)的双向总车道数,条N路网节点集合NI交叉口节点集合NR路段节点集合pbestpt粒子p历史最小的适应度qrsO-D对r-s之间的交通流量,veh/hR1,R2[0,1]间均匀分布随机数RI设置可变车道交叉口岔口的集合Rjs路段连线(j,s)设置的可变车道数,条RR设置可逆车道路段连线的集合t向量(…,ta,…),∀a∈Ata连线a的阻抗(时间),htij交叉口连线(i,j)上的阻抗(时间),htjs路段连线(j,s)上的阻抗(时间),htjs路段连线(j,s)的基本阻抗(时间),hTHCM延误模型中分析时段vmax粒子群算法中的粒子最大更新速度vpt粒子p在第t次迭代中的更新速度w粒子群算法中的惯性权因子x向量(…,xa,…),∀a∈A

x*下层问题的用户平衡解xa连线a的交通流量,veh/hxij交叉口连线(i,j)上的交通流量,veh/hxBij交叉口连线(i,j)上的公交车流量,veh/hxjs路段连线(j,s)上的交通流量,veh/hxBjs路段连线(j,s)上的公交车流量,veh/hxEjs路段连线(j,s)上的紧急救援车流量,veh/hzpt粒子p在第t次迭代中的位置α,βBPR模型中的参数σrsa,k若连线a在O-D对r-s之间路径上,为1;否则为0ε收敛检验参数ξjs路段连线(j,s)紧急救援车通过的时间限制,h

3研究方法

3.1基础路网描述

对于一个路网G=(N,A),节点集合为N,连线结合为A。其中,节点集合N分为交叉口节点集合NI和路段节点集合NR两类;连线集合A分为交叉口连线集合AI和路段连线集合AR两类。以图2为例:(1)对于一个n岔交叉口,可用n个交叉口节点分别表示交叉口的各进口i,j,k,l,m∈NI;(2)对于路段,可在相邻两交叉口节点间插入一个路段节点,h,s∈NR;(3)对于交叉口内部流向由两个交叉口节点构成的交叉口连线表示(i,j)∈AI,∀j,k∈NI;(4)若构成连线的两个节点中存在路段节点,则该连线为路段连线,表示交叉口间路段的流向,(j,s)∈AR,∃j,s∈NR。

图2　路网构成示意

3.2交通需求描述

根据不同类型车辆出行特性的不同,将交通需求分为3类,如表2所示。

表2　交通需求构成

3.3优化模型建立

采用双层规划方法,建立应对城市交通拥挤和大型活动的可逆车道设置优化模型。

3.3.1上层问题

上层问题的目标是使系统总出行时间最小,如式(1)所示

(1)

约束条件包括:

(1)车道数约束。任一连线的车道数包括基本车道数和可变车道数,可按式(2)、式(3)计算。路段总车道数以及交叉口进出口总车道数都应为定值,分别如式(4)～式(7)所示。同时车道数有非负性和整数的要求,如式(8)所示

(2)

(3)

njs+nsj=njs,sj,∀(j,s),(s,j)∈AR

(4)

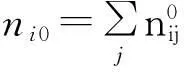
(5)

(6)

ni0+nir+nih=ni,∀(i,h)∈AR

(7)

(8)

(2)交叉口出口道约束。为保证交叉口畅通,交叉口进口任一流向的车道数均不应大于相应出口的车道数,如式(9)所示

njs≥nij,∀(i,j)∈AI,∀(j,s)∈AR

(9)

(3)可逆车道设置一致性约束。为保证设施的连贯性,在同一路段和进口道的可逆车道设置应保持一致性,如式(10)所示

(10)

(4)公交车辆约束。对于存在公交线路的连线,其车道数需>0,如式(11)所示

(11)

(12)

(5)紧急救援车辆约束。对于任一紧急救援通道上的连线,该连线至少需设置一条可逆车道供紧急救援车辆在需要时使用,如式(13)所示

(13)

3.3.2下层问题

下层问题采用随机用户平衡(SUE)配流模型。本研究对于路段连线的出行阻抗如式(14)所示。对于交叉口连线,可采用如式(15)所示的方法

(14)

tij=d1ij(PF)+d2ij+d3ij,∀(i,j)∈AI

(15)

(16)

(17)

由于上述出行阻抗是不对称的,因此下层问题变为非对称影响的SUE问题。Dafermos(1980)[11]证明该问题可由变分不等式模型来描述。因此,下层问题可由式(18)表示

t(x*)T(x-x*)≥0,∀x∈K

(18)

(19)

3.3.3可变车道设置位置确定

(20)

(21)

(22)

3.4求解方法

本文采用粒子群优化算法来对模型进行求解,对于其中的下层非对称影响的SUE配流问题,应用结合了MSA算法的“对角化”算法求解。

(23)

(24)

算法步骤如下:

步骤1(初始化)设置最大速度υmax、缩小系数θ,η(0<θ<η)、动态延迟期和粒子群规模P等参数,产生p个可行粒子,赋每个粒子初始速度;

步骤2(计算适应度)针对每个可行粒子,计算此时其上层目标函数值,即为该粒子此时的适应度;

步骤4(计算新位置)根据式(24)计算各个粒子的新位置;

步骤6(终止检验)若满足终止准侧,停止迭代,输出最后的gbestt作为优化结果。否则令t=t+1转至步骤2。

(2)下层问题算法。对于非对称问题,Fisk(1982)[12]研究表明“对角化”算法是求解该问题的最有效的方法。对于SUE问题可采用MSA算法求解[13]。算法步骤如下:

步骤1(初始化)从中取定一个向量x0,令q=0;

步骤3(解对角函数)关于对角函数t(x,xq)的变分不等式问题就是解一个SUE问题,采用MSA算法求解,得到xq+1;

3.5算例

图3　简单网络

本文采用一个简单的双向交通网络来验证所提出的模型与算法的有效性。对此网络中的24条路段及16个进口道进行优化。交叉口节点数从1～16,路段节点数从17～28。初始每一路段单向车道数为3车道,每一进口交叉口的车道数为3车道;单向每一车道的理论通行能力为800 pcu/h。

在上层问题中,置初始惯性因子w0=1.4,最大速度为vmax=[2,2,2,2],缩小系数θ=η=0.98及动态延误期h=5,设粒子群规模为m=20,最大允许迭代次数itermax=50。当算法程序达到最大允许迭代次数时,停止迭代,输出最优值。

在下层问题中,给定α=0.15,β=4;CI(I=1,…,16)的信号周期时长为90 s;gij=45 s。通过Matlab编程,对给定的基础路网进行优化,可得出如图5优化后的分配路网。经计算,系统总出行时间降低了20%。证明该可逆车道的设置是合理有效的。

图4　优化后路网

4结束语

本文建立一种应对城市交通拥挤和大型活动的可逆车道设置位置优化模型。采用双层规划进行求解,同时,文中给出了模型的求解方法,对于上层问题采用粒子群优化算法求解,对于下层采用结合了MSA算法的“对角化”算法求解。本文研究成果适用于在管理规划层面针对现有路网选择合适的可逆车道实施地点,模型算法的考虑因素较多,导致求解时间较长。对于可逆车道的实时控制问题,有待进一步研究。

参考文献

[1]上海市城市综合交通规划研究所.上海市第四次综合交通调查[R].上海:上海市城市综合交通规划研究所,2011.

[2]Addenda.A policy on geometric design of highways and streets (green book)[M].Washington D C:American Association of State Highway and Transportation Officials,2001.

[3]Institute of Transportation Engineers.Traffic engineering handbook[M].Washington D C:Institute of Transportation Engineers,2009.

[4]U.S.Department of Transportation.Manual on uniform traffic control devices[M].Washington D C:Federal Highway Administration,U.S.Department of Transportation,1988.

[5]Matthew Hausknecht,Tsz-Chiu Au,Peter Stone,et al.Dynamic lane reversal in traffic management[C].Washington DC:2011 14th International IEEE Conference on Intelligent Transportation Systems,2011.

[6]翟忠民.道路交通组织优化[M].北京:人民交通出版社,2004.

[7]Liang Xiao,Hu Chunping,Ma Chaoyun,et al.Empirical study on variable lanes design of chaoyang north street in beijing[C].Yantai,China:Proceedings of the 30th Chinese Control Conference,2011.

[8]张好智.城市道路交通网络设计问题的相关优化模型与算法[D].北京:北京交通大学,2007.

[9]Chi Xie,Mark A Turnquist.Lane-based evacuation network optimization:an integrated lagrangian relaxation and tabu search approach[J].Transportation Research Part C,2011,19(1):40-63.

[10]Ampol Karoonsoontawong,Dung linying.Time-varying lane-based capacity reversibility for traffic management[J].Computer-aided Civil and Infrastructure Engineering,2011,26(8):632-646.

[11]Defermos S C.Traffic equilibrium and variational inequalities[J].Transportation Science,1980,14(1):42-54.

[12]Fisk C,Nguyen S.Solution algorithms for network equilibrium models with asymmetric user costs[J].Transportation Science,1982,16(3):361-381.

[13]Sheffi Y,Powell W B.A comparison of stochastic and deterministic traffic assignment over congested networks[J].Transportation Research Part B,1981,15(1):53-64.

中图分类号TP319;U491

文献标识码A

文章编号1007-7820(2016)03-007-05

doi:10.16180/j.cnki.issn1007-7820.2016.03.003

作者简介:叶静茹(1990—),女,硕士研究生。研究方向:交通运输工程。马晓旦(1966—),男,副教授,硕士生导师。研究方向:交通规划等。

基金项目:国家自然科学基金重点资助项目(51238008)

收稿日期:2015- 11- 19