奇特的六位数

林革

亨利·欧内斯特·杜登尼是19世纪英国知名的趣味智力题作家，某一天，他收到一封慕名请教的读者来信，信中除了对大师的崇敬和恭维，还请求解答一道有关六位数的难题。杜登尼一下子就被这道题吸引住了：求一个六位数，当它用2、3、4、5、6乘后，仍是一个六位数，但它们的全部数字却一样，只不过是它们的组成顺序不同而已。

要确定如此特殊的六位数谈何容易，这条件简直是天马行空、难以琢磨，甚至苛刻到无从下手。杜登尼思考了很久，乍看起来，要找到具备如此特性的数无异于大海捞针，难怪这位读者被搞得神魂颠倒茶饭不思呢。

经过几天的苦思冥想杜登尼仍无进展，心情沮丧却又无奈。他觉得如此纠结下去不是办法，不如暂且放下，让自己轻松轻松，于是他丢下写得密密麻麻的草稿纸，随手拿起一本数学书籍浏览起来。当他无意读到有关循环小数的内容时，出于职业的本能信手在纸上计算起诸如[13]、[16]、[17]……这些可化成循环小数的分数，当写到[17]=0.142857时，仍惦记着刚才那道六位数难题的杜登尼喃喃自语：“这个循环节倒是个六位数，要是它恰好是读者问题的答案，那就真是上帝的指点或暗示了。”很明显，此时自我调侃的他，并没有意识到一个神奇的发现即将诞生。

当杜登尼继续带有偶然随意试算[27]、[37]、[47]、[57]、[67]时，突然眼前一亮，他发现[27]=0.285714、[37]=0.428571、[47]=0.571428、[57]=0.714285、[67]=0.857142，结果都是循环小数，而且它们的循环节也都是由1、4、2、8、5、7这六个数组成，只不过顺序不同，那么那道六位数的难题的答案就是142857？

验算非常简单：142857×2=285714，142857×3=428571，142857×4=571428，142857×5=714285，142857×6=857142。

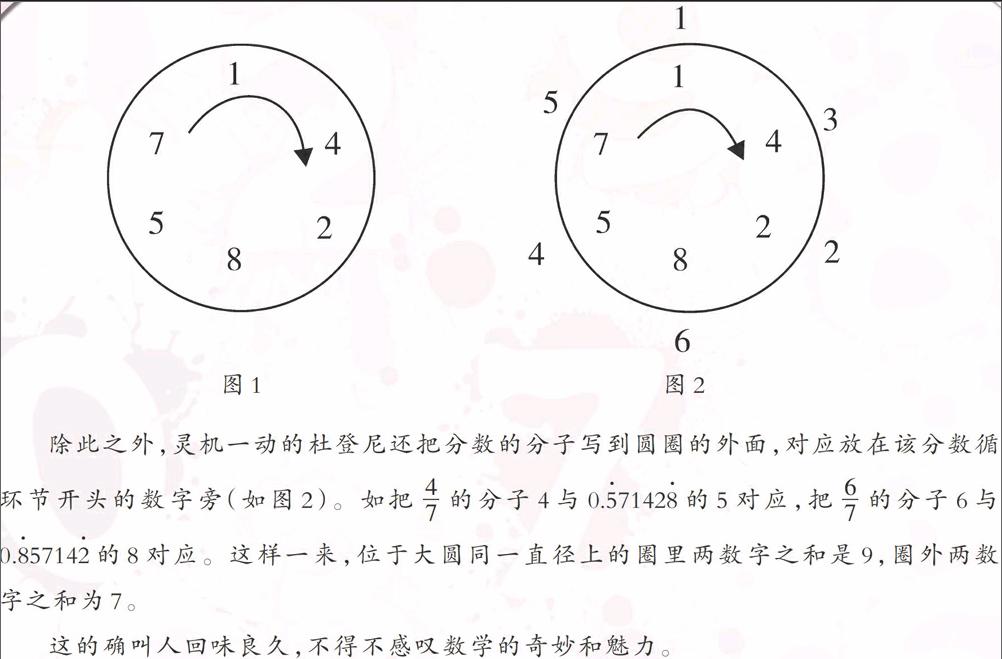
意犹未尽的杜登尼情不自禁反复打量这个神奇的六位数，很快就又有所发现：把142857按顺时针方向依次写在一个圆圈里面（如图1），那么它与2、3、4、5、6相乘后的结果，就是从圆圈中的某数开始，按照顺时针方向依次逐个写出后续数。比如142857×5就是从首位7开始，按箭头所示写出后面的数字得到714285。

除此之外，灵机一动的杜登尼还把分数的分子写到圆圈的外面，对应放在该分数循环节开头的数字旁（如图2）。如把[47]的分子4与0.571428的5对应，把[67]的分子6与0.857142的8对应。这样一来，位于大圆同一直径上的圈里两数字之和是9，圈外两数字之和为7。

这的确叫人回味良久，不得不感叹数学的奇妙和魅力。

兔博士讲堂

142857这六个数确实是一组神奇的数，当你用它乘以7，看看有什么结果——

142857×7=999999

再把142857这个数字分解成两组数字：142，857 ，这两个数字之和为142+857=999 ；

再把142857分解成三组数字：14，28，57 ，这三组数字之和为14+28+57=99 ；

最后我们把142857再乘于142857，结果是142857×142857=20408122449 ；

再把20408122449分解两组数字：20408和122449 ，它们之和是：20408+122449=142857。

游戏结束！

是不是觉得这些数字很神奇？

相传，142857这组数发现于埃及金字塔内，它证明一星期有7天，它自我累加一次，就由它的6个数字，依顺序轮值一次， 到了第7天，它们就放假，由999999去代班，数字越加越大，每超过一星期轮回，每个数字需要分身一次， 你不需要计算机，只要知道它的分身方法，就可以知道继续累加的答案。

关于这组数，还有很多更神奇的地方等你去发掘，也许，它就是宇宙的密码！