基于连续小波阈值函数的语音增强技术
陆 真,裴东兴
(1.中北大学 电子测试技术国家重点实验室,山西 太原 030051;
2.中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
基于连续小波阈值函数的语音增强技术
陆真1,2,裴东兴1,2
(1.中北大学 电子测试技术国家重点实验室,山西 太原 030051;
2.中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
摘要:在语音信号处理过程中,语音增强目的是尽可能恢复出纯净的原始语音信号。针对纯净语音易被环境噪声污染的问题,提出一种连续的阈值函数,并给出具体推导过程。该函数在一定程度上克服了传统函数的非连续不可导等问题。语音小波系数经过该函数处理后,语音质量得到改善。仿真结果表明:该函数在一定程度上提高了语音识别系统前端预处理的抗干扰能力,输入语音的信噪比得到了提高。
关键词:语音增强;阈值函数;信噪比;小波变换
在通信系统中语音会不可避免地受到来自周围环境、传输媒介引入的噪声干扰。这些干扰信号最终导致接收到的语音信号并非是纯净的原始语音信号。由于噪声导致语音质量的下降会使许多语音处理系统的性能急剧恶化,所以,采用语音增强技术进行预处理,将有效地改善系统性能[1,2]。
小波分析是近年来迅速发展起来的一种时频域局部分析法。在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率。克服了短时傅里叶变换固定分辨率的缺点,能够将信号在多尺度分辨率上进行小波分解,特别适合用来分析处理语音这种非平稳信号[3]。目前小波变换法实现语音增强主要有三种方法:小波阈值去噪法、小波模极大值去噪法、基于小波系数尺度空间相关性去噪法。
目前小波阈值去噪法的应用最广,而噪声阈值估计和合理的阈值函数是该算法的关键技术。Donoho D.L.在理论上证明了利用小波阈值去噪的合理性[4]。之后又提出了小波阈值变换法并提出了软硬阈值函数[5]。随后,学者们相互又提出多种改进的阈值函数[6],取得了一定的语音增强效果,克服了传统函数的不足,但这些函数的不连续性,容易导致语音产生附加噪声,降低了语音的舒适度。本文提出一种连续可导的小波阈值函数,结合最佳阈值估计,来达到对噪声污染语音进行增强的目的。
1小波阈值去噪技术
1.1语音信号特征
人的发声器官由三部分组成:肺和气管产生气源;喉和声带组成声源;咽腔、口腔、鼻腔组成声道。空气由肺部排入喉部,经过声带进入声道,最后由嘴辐射出声波,从而形成语音。在声带开启时,空气流从声门喷射出来,形成一个脉冲,声带闭合时相应于脉冲序列的间隙期。此时,在声门处产生一个准周期脉冲状的空气流,该空气流经过声道后最终从嘴唇辐射出声波,产生浊音。基频是语音特征中的一个重要参数,声带张开闭合的周期决定了基音频率。男性的基因频率为50~250 Hz,女性基音频率一般为100~500 Hz。清音是肺部发出的空气流不受影响的通过声道或声道突然完全闭合而形成。语音的共振峰是声音在声道传输中,其频谱会受到声道共振特性的影响,声道而具有的一组共振频率[7]。
听觉感知主要是测试响度、音高和掩蔽效应。人耳界限频率范围大约为20 Hz~20 kHz,语音的感知强度范围为0~130 dB[8]。图1为听觉模型的一般原理框图。响度是频率和强度级的函数,音高被称作基音,与响度互为补充。掩蔽效应是两个响度不等的声音作用于人耳时,响度较高的频率成分会影响对响度较低频率成分的感受,使其不容易被察觉。

图1 听觉模型一般原理框图
1.2小波阈值去噪的理论
小波变换的定义为:

(1)
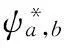
小波重构是小波变换的逆过程。由于处理的数字语音信号,为了减小计算量,缩减小波系数信息量的冗余,需要对小波变换进行离散化,即将(1)式中a=2-j,b=k2-j,j,k∈Z。为了提高小波变换的速度,Mallat提出了mallat算法。该算法大大降低了小波变换的计算量,成为处理非平稳信号的一种强有力的工具。
小波阈值去噪法的基本思想是对小波变换后的语音高频信号设定最优阈值,大于该阈值的信号保留,屏蔽掉小于阈值的信号,经过阈值处理后的高频小波系数和近似低频信号重构出增强的语音。
1.3小波阈值的估计
小波语音增强过程是比较关键的,小波阈值的选取在整个语音增强过程中是比较关键的一步,一般需要通过经验选取。阈值估计一般有局部阈值估计法、全局阈值估计法和区域阈值估计法。其中全局阈值估计更能适应于实际情况,但是其计算量要高于局部阈值估计[9]。通常选用阈值为:sqtwolog、rigrsure、heursure和minimaxi规则。
1) sqtwolog规则:被测信号中含有独立同分布的噪声时,经过小波变换后,其噪声的小波变换系数是独立同分布的。若具有独立同分布的噪声经过小波分解后,它的系数序列长度很长,根据通用阈值理论,存在一个阈值,使得该序列的所有小波系数都小于它。随着分解层数的增大,小波系数的长度也越来越短,故在噪声独立分布的情况下,可以通过设置阈值函数来达到增强的目的。
2) rigrsure规则:该阈值是利用Stein的无偏估计求出的SURE阈值。其根据其阈值产生的风险函数曲线和最小风险点来确定Stein无偏风险阈值。
3) heursure规则:启发式阈值是通用阈值和regrsure阈值的综合体,是最优的预测变量阈值选择。当输入信号的信噪比较小时,SURE的估计会有很大的误差,此时应该采取固定的阈值准则。
4) minimaxi规则:极大极小阈值采用的是一种比较固定的阈值,它将产生一个最小均方误差的极值,是有一定的误差。
2阈值函数的选取
2.1传统小波阈值函数
阈值函数与重构信号的精度和连续性有关,影响着小波去噪的效果。硬阈值函数和软阈值函数是目前最常用的两种阈值函数,图2(a)为硬阈值方法,图2(b)为软阈值方法,其中,ω是小波系数的大小,ωλ是施加阈值后小波系数的大小。

(a) 硬阈值函数示意图(b) 软阈值函数示意图
图2最常用的两种阈值函数
硬阈值的性质决定了它处理的信号具有不连续性,软阈值的性质决定了它具有比硬阈值更好的连续性,但它的导数却是不连续的,估计小波系数与带噪小波系数存在恒定偏差,而且对于大于阈值的系数进行定值压缩与噪声随小波系数增大而减小的事实不符合。
2.2新的阈值函数
传统的小波函数由于存在自身的不足,在处理信号后不能达到理想的效果。本文提出一种新的阈值函数,它既能实现阈值函数的功能,又具有二阶甚至更高阶以上的连续导数。
利用指数函数的特点,引入一种新阈值函数为:

(2)
其中,α为一待求常数。可见,上式与软阈值函数的趋势相符。令β=1,分别等于1、2、3代入上式,当α取不同值时,所对应的函数图形差别较大,因此,在应用中必须选择合适的α值才能得到最佳效果。
令x=-x代入上式后,得:

(3)
所以,改进的阈值函数是一个奇函数。若要求改进阈值函数单调递增,则需要满足:
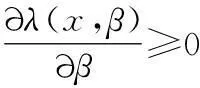
(4)
对于分母,满足:

(5)
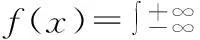
(6)
由以上分析,进一步可得:
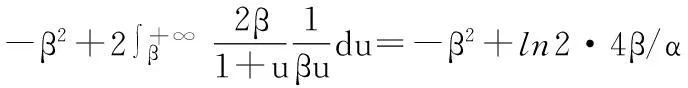
(7)
故当α=2/β时,f(x)取得最小值,故改进的阈值函数为:
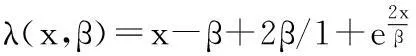
(8)

图3 本文阈值函数示意图
如图3所示,该函数对比阈值较小值进行一定的平滑度处理,并且在选定阈值处具有连续性,克服了传统阈值函数的缺点,在大于选定阈值处,阈值趋于y=x直线,减小了固定偏差的问题。该函数具有连续性,且高阶可导,减小了自身对语音信号的影响。
3实验结果分析及评价
实验条件:语音样本通过Praat软件录制“中北大学电子测试重点实验室”2.25 s语音,采样频率为8 kHz。通过高斯添加高斯白噪声来控制语音信号的输入信噪比。语音分析采用的帧长为256,选择50%的重叠,窗函数为汉明窗,小波基选用db4,对语音帧进行3级分解。评价标准选用信噪比和均方误差[10]。信噪比反映的是信号的感知质量,表达式如式(9);而均方误差反映了估计值和实际值的相似程度,其值越小相似度越高,表达式如式(10)。以上评价指标定义如下:

(9)
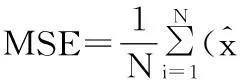
(10)
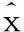
表1为不同输入信噪比下,三种阈值函数在Stein无偏风险估计阈值下增强语音的输出信噪比SNRout和均方误差MSE。

表1 三种阈值函数增强语音SNRout和MSE的数据比较
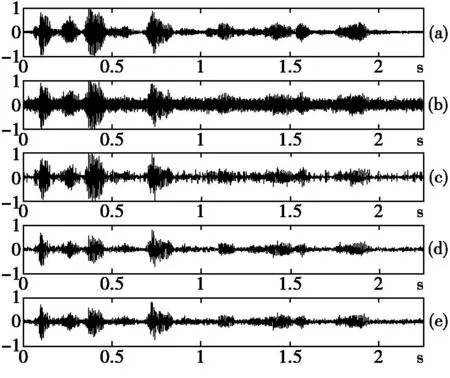
图4 (a)原始语音波形,(b)输入信噪比为1.68被污染的语音波形,
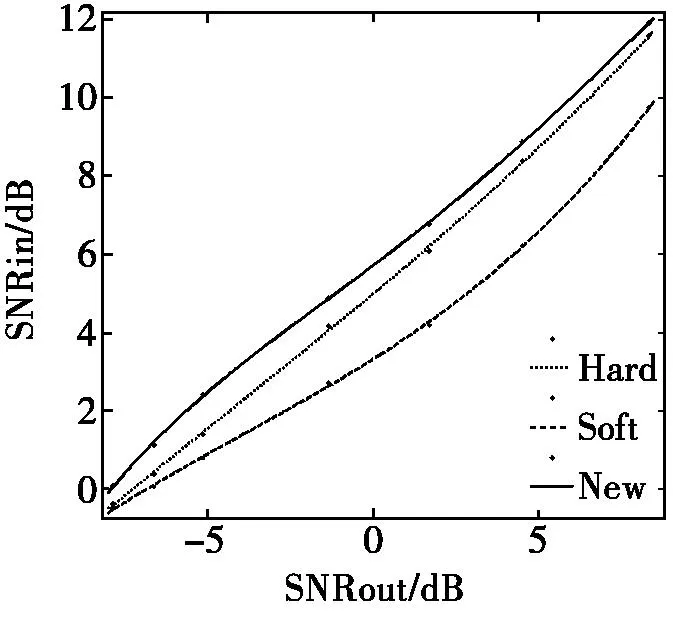
图5 三种阈值函数语音增强效果的比较
图4是输入信噪比为1.68时,分别对其进行硬阈值函数、软阈值函数和本文阈值函数得到的语音增强后归一化波形。图5为三种阈值函数下输出信噪比与输入信噪比的趋势图。
1) 在三种阈值函数去噪方法下,可以看出,改进阈值函数明显优于其它两种方法;
2) 在输入信噪比相同的情况下,本文阈值函数法的语音增强效果明显,特别是在输入信噪比小于零时;
3) 从语音的舒适感和可懂度上看,本文阈值函数的效果优于软、硬阈值函数。
4结论
由于噪声来源众多,在不同的应用场合其特性又各不相同,其增加了语音增强算法的复杂性。要实现对语音增强质量的客观评价,需从语音的清晰度和可懂度两个方面入手。传统的阈值函数一般是分段函数,由于它的不连续性容易导致处理后的语音产生畸变,如残留的音乐噪声,而影响了语音的质量。本文提出了一种阈值函数,该函数具有连续可导性,并给出具体的数学推导表达式,并结合rigrsure规则下的阈值来对污染的语音信号增强。仿真结果表明:新阈值函数克服了传统的阈值去噪的缺点,引入更少的噪声且语音舒适感更强。
参考文献
[1]李轶南,张雄伟,曾理,等.改进的稀疏字典学习单通道语音增强算法[J].信号处理,2014(1):44-50.
[2]赵力,黄程韦.实用语音情感识别中的若干关键技术[J].数据采集与处理,2014(2):157-170.
[3]陶华伟,査诚,梁瑞宇,等.面向语音情感识别的语谱图特征提取算法[J].东南大学学报(自然科学版),2015(5):817-821.
[4]Donoho D L.De-noising by Soft-thresholding[J].IEEE Trans Inform Theory,1995,41(3):613-627.
[5]Donoho D L,Johnstone I M.Ideal Spatial Adaption by Wavelet Shrinkage[J].Biometrika,1994,81(2):425-455.
[6]徐志夺.基于小波变换的语音增强算法研究[D].哈尔滨:哈尔滨工程大学,2013.
[7]玄成君.基于语音频率特性抑制音素影响的说话人特征提取[D].天津:天津大学,2014.
[8]颜利君.基于噪声估计和掩蔽效应的语音增强[D].成都:西南交通大学,2014.
[9]周氏青香.听觉特性及噪声估计在语音增强算法中的研究[D].上海:华东理工大学,2013.
[10]张波.基于DSP助听器的响度补偿技术研究[D].太原:中北大学,2014.
The Algorithm of Image Denoising Based on the Optimized Wavelet Thresholding Function
Lu Zhen1,2, Pei Dongxing1,2
(1.NationalKeyLaboratoryforElectronicMeasurementTechnology,NorthUniversityofChina,TaiyuanShanxi030051,China;2.KeyLaboratoryofInstrumentationScience&DynamicMeasurementofMinistryofEducation,NorthUniversityofChina,TaiyuanShanxi030051,China)
Abstract:For the problem that the signal of digital hearing aid is interfered by background noise in the process of receiving and processing, a kind of optimized de-noising algorithm is put forward based on traditional method of wavelet threshold. It has the feature of higher order continuous differentiable, and additionally, the problem of indifferentiable with the traditional method of wavelet thresholding is solved. This threshold function can be used to process the wavelet coefficient of speech signal with noise to have a speech de-noising effect. Eventually, the simulation results show that compared to the noise ratio(SNR),the mean square error(MSE) and speech intelligibility of the speech de-noising signal with the new threshold function the signal are superior to the other non continuous differentiable thresholding function.
Key words:speech signal de-noising; wavelet transform; speech intelligibility; threshold de-noising
中图分类号:TN912.35
文献标识码:A
文章编号:1674- 4578(2016)01- 0040- 03
作者简介:陆真(1988- ),男,湖北襄阳人,硕士研究生,研究方向:动态测控与智能仪器、数字语音与图像信号处理。
收稿日期:2015-09-21修回日期:2015-10-29

