满足可靠性要求的继电保护装置预防检修模型

王玉财，吕飞鹏，何 奎



满足可靠性要求的继电保护装置预防检修模型

王玉财，吕飞鹏，何 奎

(四川大学电气信息学院，四川 成都 610065)

对继电保护装置进行预防性检修，能够有效提高保护装置的可靠性。采用威布尔分布模型，引入故障率递增因子，对预防检修作用下保护装置的失效率模式进行了分析。在此基础上，以预防检修平均费用函数作为目标函数，以保护装置的可靠度作为约束条件，构建了满足可靠度要求的保护装置预防检修模型，并且利用MATLAB软件对该模型进行求解以得到最佳的检修周期和检修次数。最后，通过算例分析了可靠度与检修费用之间的关系以及故障率递增因子对检修策略的影响。该研究对检修部门制定检修计划具有一定的参考意义。

继电保护；可靠性；预防检修；故障率递增因子；检修周期

0 引言

继电保护系统是保证电网安全运行的第一道防线，其自身可靠性直接关系着电力系统和主设备的安全稳定运行[1-2]。对继电保护装置进行预防性检修是提高保护系统可靠性的有效措施。检修周期的确定是影响预防性检修效果的一个主要因素，如果检修周期过短，一方面会增大运维人员的工作量，另一方面会使设备的折损加快，不利于企业的经济运行。如果检修周期过长，则保护系统的可靠性得不到保证，同样不利于企业的经济运行。目前已有诸多文献对预防检修的最佳检修周期进行了探讨。例如文献[3]建立保护动作的状态空间模型，以保护的可用度最大为目标，确定最佳的检修周期。文献[4]为研究保护装置的可靠性定义了继电保护经济性指标。文献[5]在文献[4]的基础上以保护年均经济损失最小为目标，建立保护系统的状态空间模型，以求解最佳的检修周期。文献[6-7]同时考虑可靠性和经济性两个指标，建立相应的状态空间模型，定义了经济成本可靠系数，以经济成本可靠系数最小为目标确定最佳的检修周期。

上述研究基本上都是以Markov状态空间法为基础，在失效率恒定的假设条件下[8]，来确定最佳的预防检修周期。但是保护装置的失效率从整个生命周期来看并不是一个常数，而是符合一般工业元件的“浴盆曲线”[9-10]，这将会影响到保护装置最佳检修周期确定的准确性。另外，现有文献只对最佳的检修周期进行了分析，较少有文献对检修的次数进行深入探讨，即经过多少次检修以后，为了保证保护系统的可靠性，需要对保护装置进行更换。

针对上述两个问题，本文首先引入故障率递增因子来描述保护装置的故障率在预防检修作用下的变化规律。然后，从保护装置的可靠性和经济性的角度出发，构建了保护装置的预防检修模型，用该模型求取最佳的检修周期和检修次数。最后，本文分析了可靠度与预防检修平均费用之间的关系，探讨了故障率递增因子对检修策略的影响。

1 预防检修策略

继电保护装置的检修方式大体上分为两种：被动检修和主动检修。被动检修又称事后检修，即故障发生后对装置进行的检修。主动检修包括状态检修和预防检修等。预防检修是每隔一定的检修周期对装置进行预防性检修，当经过个周期的预防性检修后对装置进行预防性更换，以使装置的可靠性满足一定的要求。其检修策略可用图1来表示。由于继电保护装置在安全性和经济性方面都有较高的要求，一旦发生故障将产生极其严重的后果，故以可靠性为中心的预防检修策略非常适合继电保护装置。

图1预防检修策略示意图

2 预防检修作用下保护装置的故障率

2.1 威布尔分布模型

本文采用双参数威布尔分布来进行保护装置的可靠性参数估计，其故障分布密度函数为[11]

(1)

故障分布函数为

(2)

可靠度函数为

(3)

由式(1)、式(3)可得故障率的表达式为

(4)

2.2 参数估计

对于线性函数中的未知参数，主要应用最小二乘估计法进行参数估算。而威布尔分布的参数是非线性的，因此，需要经过变换将参数线性化，再利用最小二乘算法对其进行估计。对式(2)连续求两次对数可得[9]：

(5)

(6)

(7)

2.3 故障率递增因子

预防检修的主要目的是提高装置的可靠性。在预防检修周期之内，如果装置发生了故障，则对装置进行故障后检修，且假设故障后检修不改变装置的故障率，即修复“如旧”。如果到达了预防检修周期，则对装置进行预防检修，装置每经历一次预防检修，其故障率将变为零，但同时故障率函数的变化率也将增大，如在第一次预防检修后，装置的故障率将变为，其中被称为故障率递增因子。依次类推，则在第次预防检修后，装置的故障率将变为

(8)

故障率递增因子描述了保护装置经过检修之后的折损现象，故上述模型在工程中具有较强的实用性。经预防检修作用后，保护装置的故障率变化曲线如图2所示。

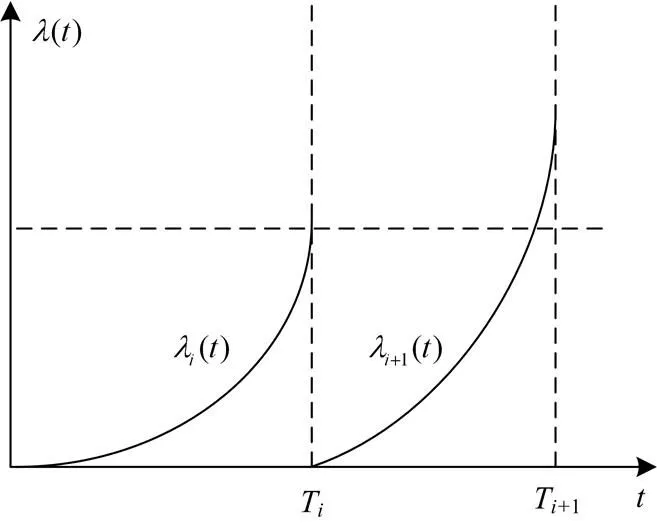
图2 故障率变化曲线图

3 预防检修数学模型

3.1 模型描述

为了简化模型和方便主要问题的研究，在构建模型时首先做如下假设：

(1) 保护装置的预防检修时间相对于整个更换周期而言很小，故可以忽略不计。

(2) 经预防检修后，保护装置的故障率将变为零。若在预防检修周期内保护装置发生故障，则进行故障后检修，故障后检修不改变保护装置的故障率。

每隔一个检修周期对保护装置进行一次预防检修，装置经预防检修后，其故障率将变为零，但是其故障率的变化率会增大倍。如果装置在检修周期内发生故障，则进行故障后检修。故障后检修不改变装置的故障率。当装置经过次预防检修后，其可靠性将不能满足系统需求，对保护装置进行预防性更换。本模型主要求解在整个装置更换周期中，在满足可靠度的约束条件下，使得装置的预防检修平均费用最低的最优检修策略。

3.2 预防检修平均费用函数分析

由上述模型描述可知，保护装置在一个更换周期内的预防检修平均费用函数可表示为

故障成本是一种惩罚性成本。保护装置故障将影响系统的正常运行和供电的可靠性，由此造成的损失费用即为故障成本。保护装置故障后造成的经济损失无法精确地估算，故本文简化将故障后维修所造成的停电损失费用作为保护装置的故障成本，其表达式如式(10)。

(10)

保护装置预防检修周期内发生故障的次数与保护装置的故障率直接相关，由保护装置的故障率可直接求出装置的期望故障次数。每个预防周期内保护装置的期望故障次数可表示为

(11)

因此，保护装置在一个更换周期内发生故障的总次数为

保护装置的一个更换周期由两部分组成，保护装置正常工作的时间以及发生故障后检修的时间，故保护装置的更换周期为

(13)

将式(8)、式(10)、式(12)、式(13)代入式(9)，整理后可得到预防检修平均费用函数的表达式为

(14)

3.3 满足可靠性要求的预防检修模型

可靠度是衡量继电保护装置可靠性的重要指标。它是指保护装置在规定的条件和规定的时间内完成规定功能的概率，即保护装置工作到某一时刻之前不发生故障的概率，可用表示。故障率与可靠度之间有如下关系：

(15)

(16)

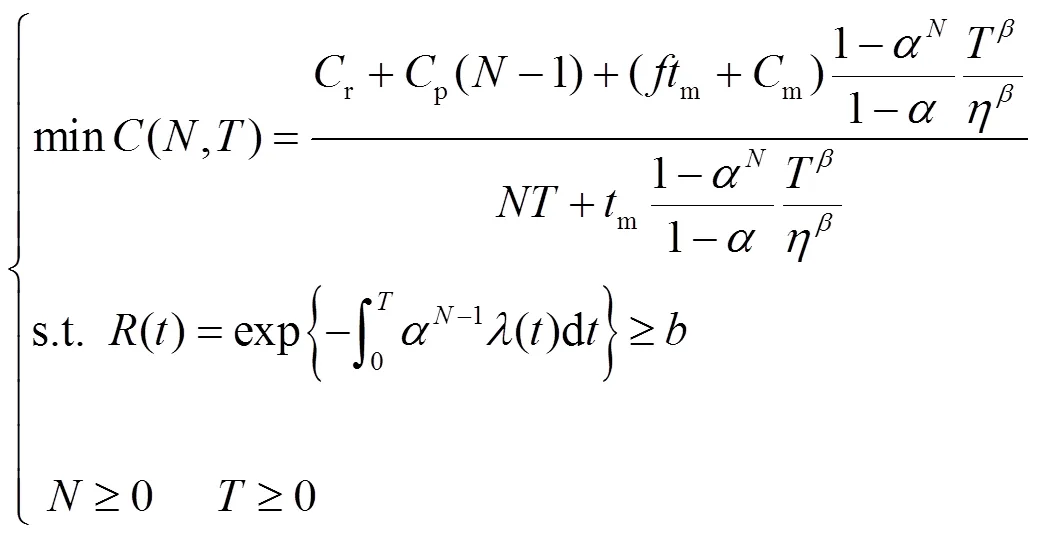
上述模型为一个有约束条件的非线性整数规划问题，可以利用MATLAB整数优化工具箱对上述模型进行求解。

4 算例分析

根据某变电站事件顺序记录系统及运行日志，可得10组保护装置的故障信息如表1所示。其中，每个故障时间对应的顺序号称为秩次。

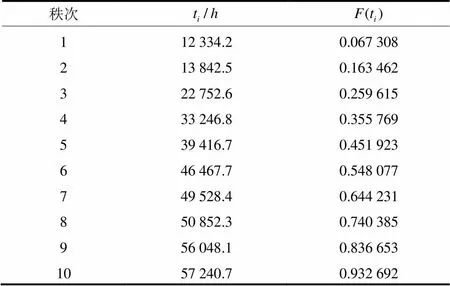
表1 保护装置的故障信息

根据2.2节的参数估计方法，可得保护装置失效率函数中的形态参数=10.63，尺度参数，即保护装置的失效率函数为

(18)

图3为保护装置可靠度与最小预防检修平均费用的关系图。从图3可以看出，在保护装置不同可靠度的要求下，得到的最优的预防检修策略不同。每个最优的预防检修策略对应着不同可靠度要求下的最小预防检修平均费用。随着保护装置的可靠度的提高，预防检修的工作也越精细，表现为设备的预防检修周期的缩短，相应的最小预防检修平均费用也会不断的上升。因此，检修部门要兼顾保护装置的可靠度要求和预防检修平均费用的要求，制定合理的检修计划。

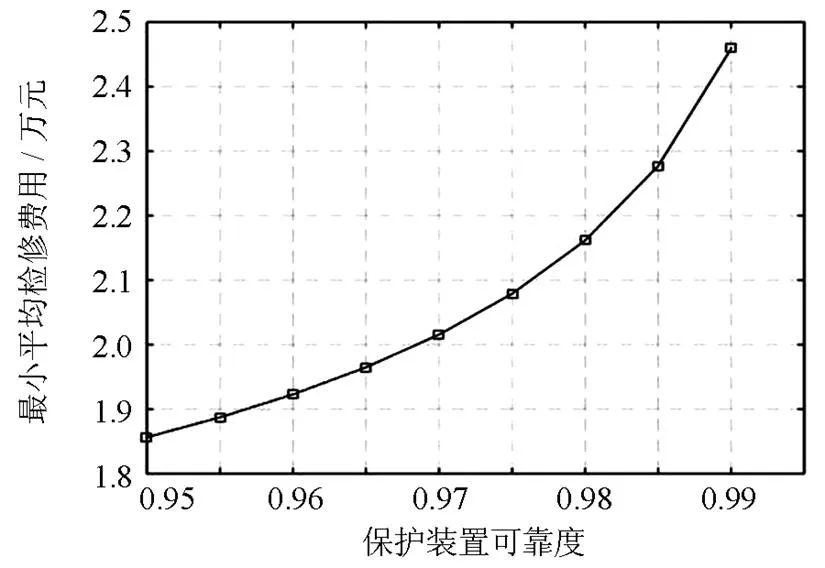
图3 保护装置可靠度与最小平均检修费用关系图

故障率递增因子与保护装置的检修效果有关，检修效果越好，则越小，反之，则越大。在可靠度约束为0.99的条件下，通过MATLAB软件可以计算得到不同故障率递增因子下的最优检修策略如表2所示。

表2 不同故障率递增因子下的最优检修策略表

从表2可以看出，故障率递增因子对最优检修策略的影响。故障率递增因子越小，保护装置的预防检修次数越多，并且检修周期越长，保护装置的利用率越高。反之，则保护装置的利用率越低。从最优检修费用上来看，最小预防检修平均费用随着故障率递增因子的增加而不断的提高，因此要想降低保护装置的检修费用，就必须提高检修人员的检修水平，尽量降低保护装置的故障率递增因子。

5 结论

本文从保护装置的可靠性和预防检修经济性的角度出发，构建了满足可靠度要求的保护装置预防检修模型并且通过算例求解得到了最佳的检修周期和检修次数。在此基础上，本文分析了可靠度与最小平均检修费用之间的关系，探讨了故障率递增因子对检修策略的影响，并且提出了相应的建议。需要指出的是，本文旨在构建保护装置的预防检修模型，针对不同的保护装置，其数据也会不同，但只需将其实际数据代入该模型即可得到保护装置的最佳检修周期和检修次数。

[1] 王同文, 谢民, 孙月琴, 等. 智能变电站继电保护系统可靠性分析[J]. 电力系统保护与控制, 2015, 43(6): 58-66.

WANG Tongwen, XIE Min, SUN Yueqin, et al. Analysis of reliability for relay protection systems in smart substation[J]. Power System Protection and Control, 2015, 43(6): 58-66.

[2] 易永辉. 继电保护装置寿命分析及寿命影响机理研究[J]. 电力系统保护与控制, 2013, 41(2): 79-83.

YI Yonghui. Research of relay protection device’s life and relative mechanism[J]. Power System Protection and Control, 2013, 41(2): 79-83.

[3] 李永丽, 李致中, 杨维. 继电保护装置可靠性及其最 佳检修周期的研究[J]. 中国电机工程学报, 2001, 21(6): 63-65.

LI Yongli, LI Zhizhong, YANG Wei. Study of reliability and optimal routine rest interval of protective relays[J]. Proceedings of the CSEE, 2001, 21(6): 63-65.

[4] 王钢, 丁茂生, 李晓华, 等. 数字继电保护装置可靠 性研究[J]. 中国电机工程学报, 2004, 24(7): 47-52.

WANG Gang, DING Maosheng, LI Xiaohua, et al. Reliability analysis of digital protection[J]. Proceedings of the CSEE, 2004, 24(7): 47-52.

[5] 丁茂生, 王钢, 贺文. 基于可靠性经济分析的继电保 护最优检修间隔时间[J]. 中国电机工程学报, 2007, 27(25): 44-48.

DING Maosheng, WANG Gang, HE Wen. The optimum routine maintenance interval of protection based on reliability economic analysis[J]. Proceedings of the CSEE, 2007, 27(25): 44-48.

[6] 郑涛, 王方, 金乃正. 双重化继电保护系统确定最佳 检修周期新方法[J]. 电力系统自动化, 2010, 34(10): 67-70.

ZHANG Tao, WANG Fang, JIN Naizheng. A novel algorithm of determining the optimal routine test interval of the dual-redundant relay protection system[J]. Automation of Electric Power Systems, 2010, 34(10): 67-70.

[7] 冯豆, 李生虎, 崔芳. 继电保护系统最优检修周期的优化算法[J]. 电力系统保护与控制, 2011, 39(21): 60-64, 69.

FENG Dou, LI Shenghu, CUI Fang. Optimization algorithm for maintenance period of protection systems[J]. Power System Protection and Control, 2011, 39(21): 60-64, 69.

[8] 薛安成, 王睿琛, 刘蔚, 等. 继电保护装置恒定失效率估算方法[J]. 电力系统自动化, 2012, 36(4): 6-10.

XUE Ancheng, WANG Ruichen, LIU Wei, et al. Estimationmethods for constant failure rate of protection equipment[J]. Automation of Electric Power Systems, 2012, 36(4): 6-10.

[9] 师元康, 姜振超, 赵书涛. 基于内部温度的继电保护装置时变失效率研究[J]. 电力系统保护与控制, 2016, 44(4): 123-128.

SHI Yuankang, JIANG Zhenchao, ZHAO Shutao. Research on time-varying failure rate of protection devices based on internal temperature[J]. Power System Protection and Control, 2016, 44(4): 123-128.

[10] 齐先军, 彭翔天, 张晶晶. 基于浴盆形故障率函数的配电系统可靠性评估算法[J]. 电力系统保护与控制, 2015, 43(5): 81-87.

QI Xianjun, PENG Xiangtian, ZHANG Jingjing. Reliability evaluation algorithm of power distribution system based on bathtub-shaped hazard function[J]. Power System Protection and Control, 2015, 43(5): 81-87.

[11] 秦金磊, 牛玉广, 李整. 电站设备可靠性问题的威布尔模型求解优化方法[J]. 中国电机工程学报, 2012, 32(增刊1): 35-40.

QIN Jinlei, NIU Yuguang, LI Zheng. Optimization approach of Weibull model solution for power station equipment reliability[J]. Proceedings of the CSEE, 2012, 32(S1): 35-40.

[12] 麻晓敏, 张士杰, 胡丽琴, 等. 可靠性数据威布尔分析中秩评定算法改进研究[J]. 核科学与工程, 2007, 27(2): 152-154.

MA Xiaomin, ZHANG Shijie, HU Liqin, et al. An improved rank assessment method for Weibull analysis of reliability data[J]. Chinese Journal of Nuclear Science and Engineering, 2007, 27(2): 152-154.

(编辑 魏小丽)

Preventive maintenance model for relay protection device based on reliability requirements

WANG Yucai, LÜ Feipeng, HE Kui

(School of Electrical Engineering and Information, Sichuan University, Chengdu 610065, China)

Preventive maintenance of relay protection device can effectively improve the reliability of protection device. This paper uses Weibull distribution model and introduces failure rate increase factor to analyze protection device failure rate model under the action of preventive maintenance. On this basis, the preventive maintenance average cost function is taken as the objective function, and the reliability degree is taken as the constraints to construct the mode of protection device preventive maintenance which meet the requirements of reliability, and MATLAB software is used to solve the model to get the optimal maintenance cycle and maintenance times. Finally, the relationship between reliability and maintenance cost and the effect of failure rate on maintenance strategy are analyzed by examples. This paper has some reference significance for the maintenance department to make the maintenance plan.

relay protection; reliability; preventive maintenance; failure rate increase factor; maintenance cycle

10.7667/PSPC151157

2015-07-06；

2015-11-02

王玉财( 1990-)，男，硕士研究生，研究方向为电力系统继电保护可靠性；E-mail: yucai_wang@163.com

吕飞鹏( 1968-)，男，教授，硕士生导师，研究方向为电力系统继电保护和故障信息智能处理系统等；

何 奎(1990-)，男，硕士研究生，研究方向为电力系统继电保护。