基于暂态能量的电力系统切机控制措施
王佳丽,刘涤尘,廖清芬,岑炳成,李 顺,齐晓曼
基于暂态能量的电力系统切机控制措施
王佳丽1,刘涤尘1,廖清芬1,岑炳成1,李 顺1,齐晓曼2
(1.武汉大学电气工程学院,湖北 武汉 430072;2.国网上海电力科学研究院,上海 200437)
为了实现更准确有效的电力系统紧急控制,提出了一种考虑惯性时间常数变化的切机量计算方法,并在加速机群进行分配。该方法基于系统等值二机系统的暂态过程能量进行求解,所需数据均可通过广域测量得到,不需要依赖电力系统的具体模型和参数,可以实现对电力系统的实时控制,计算量小,方便灵活。同时考虑了在切机过程中系统的惯性时间常数的变化,使得切机控制更加准确。通过对新英格兰10机39节点算例的仿真分析,验证了该控制方案的有效性。
暂态稳定;切机;惯性时间常数;实时控制
0 引言
我国幅员辽阔,受到资源分布、环境因素和经济差异的制约,电网结构凸显出跨区互联、远距离、大容量输电、交直流相结合等特征,电网的规模越大,电网的稳定问题也愈加严峻[1-3]。电力系统的失稳事故可能引起工业和居民断电,甚至可能使电力系统崩溃,给我国经济造成重大损失,需及时采取各种控制措施使其恢复稳定[4-5]。
系统发生安全稳定问题后,需要及时采取合适的紧急控制措施,其中一个重要的暂态稳定控制措施是切机措施[6-7]。切机控制策略的制定包含切机地点的选择、切机时刻和切机量的求取三个方面。其中合理而有效的切机量是保证系统恢复稳定的重要因素,同时快速准确计算出切机量也是实现紧急控制的快速性必不可少的条件,系统故障后的切机量化方法研究一直是人们的关注点。近年来,广域测量系统迅速发展,为切机控制策略提供了技术条件[8-9]。文献[10]以改进支路能量函数法为理论基础,求取并网系统故障后所需切机量。文献[11]通过分析暂态能量函数,根据故障后的稳定裕度来确定所需的切机量。但是能量函数法难以区分系统中发电机内部和发电机间的能量,因此利用能量函数法来求取的切机量,难免其中包含一些实际对暂态稳定无贡献的能量,造成不必要的过切[12-13]。文献[14]根据扩展等面积法求得的稳定裕度定义了切机的代价,以此确定最合适的切机控制策略,但是存在着难以确定积分起止条件以及积分路径等问题。文献[15]将系统等效为二机系统,通过计算未消纳的加速能量,进而得到系统所需切机量。不受系统运行方式的束缚,使用方便灵活,但是推导过程中并没有考虑切机导致的系统惯性时间常数的变化对切机量的影响,从而影响控制效果。
广域测量系统(Wide Area Measurement System,WAMS)已经成为我国电力调度自动化系统十分重要的组成部分[16-18]。广域测量系统得到的数据完全来源于相量测量单元(Phasor Measurement Unit,PMU)的真实数据,可以反映系统真实的动态行为[19]。本文基于WAMS测量得到的数据,在前人研究的基础上,考虑了系统惯性时间常数对系统所需切机量影响,说明在切机过程中可能伴随着系统惯性时间常数的改变,从而导致实际所需切机量的变化,并在此基础上,说明了基于系统等值二机系统的暂态能量,进而提出了考虑系统惯性时间常数的切机决策方案,为了与文献[15]进行对比,同样采用基于转速差—功角差相平面轨迹判断系统功角稳定的方法对系统进行实时监测,作为紧急控制的启动条件,并在新英格兰10机39节点的算例中进行仿真,说明了本文方法的有效性和更优越的控制效果。
1 系统惯性时间常数
惯性时间常数的物理意义如下:原动机将额定转矩加到空载的发电机转子上,静止的转子加速到额定转速所需的时间。惯性时间常数越小,在转子上施加相同的转矩,转子的运动速度变化越快。电力系统惯性时间常数是对暂态稳定有很大影响的重要的系统运行参数。
以二机系统为例,如图1,发电机的动态方程可表示为式(1)和式(2)。

图1二机系统示意图
(2)
式(3),式(4)可以表示二台发电机的电磁功率。
(4)
(6)
式(1)减去式(5)并考虑(5)和式(6)可得
式(7)可以改写为式(8),即将两机系统转化为单机系统形式。
(8)
直接法暂态稳定的相关理论指出,系统暂态稳定能力与暂态过程中积蓄的能量有直接关系[20],可以由式(9)看出,暂态能量值与发电机惯性时间常数有关,会随之发生变化,说明系统的暂态稳定水平会受到机组惯量的影响,而在实际切机过程中,是整台发电机退出运行的,此时系统的惯量会随着机组的退出运行而发生改变,进而使系统在发生暂态事故时所需的切机量随之发生变化。
2 考虑惯性时间常数的基于暂态能量的切机量
2.1 多机系统的暂态能量
一个具有台发电机的系统,其中第台发电机的动态方程表示如下:
多机系统故障后若发生功角稳定问题,在开始的一段时间内,失稳通常都表现为二机群形式的功角摆开。不论,的复杂程度,也不论各机的运行状态,将台机分割为两个非空的互补机群,有且仅有种不同的情况,它们满足如下关系:
设受扰后功角超前的机群为机群,剩余机群称为机群,它们都有对应的惯量中心。把机系统映射到两机系统。
(12)
其中:
由此,可把式(10)系统的运动方程变换为
(15)
其中
将式(16)代入式(15),得
(17)
对等值后的单机系统功角曲线进行分析,功角曲线如图2所示。

图2 等值单机系统功角曲线
(18)
故
2.2 考虑惯性时间常数变化的切机量
(20)
若要使实施控制后系统恢复稳定,需要使减速面积的增加量为
则可知
(22)
在计算出对应等值系统的总切机量后,由于切机量在加速机群中按机组出力情况进行分配,故每台机组的切机比例相同,假设每台机组均由不同数目的相同发电机组成,则认为每台机组减少的惯性时间常数相同,根据式(13),加速机群的惯性时间常数减少相同的比例,设为,可以列出如下方程组:
由式(24)可得切机功率为
(25)
求得切机功率后,根据加速进群中各机组的输出功率情况,再进行分配切机量。
3 紧急控制方案
3.1 暂稳辨识方法
为跟文献[15]进行对比,采用基于相轨迹的失稳判断方法。在相平面,如果系统稳定,相平面上发电机的运动轨迹将从第四象限越过横轴回到第一象限,然后进入回摆过程,功角不会趋于无穷大;若系统不稳定,则轨迹将会在第一象限的某点向远处开始进行发散,功角越来越大。由于电力系统时一般存在一定的安全裕度,所以故障发生后系统一般首先会经历一段时间的减速阶段,而系统失稳则是由于减速能力不足,导致系统再次进入加速阶段,即轨迹会出现一个“下凸点”,这标志着系统将失去稳定。
若曲线在某点处的二阶导数等于零,则曲线上在该处出现拐点,即;当时,曲线在该区间为凹函数;当时,曲线在该区间为凸函数[23]。系统失稳,则轨迹会由凹函数转变为凸函数,实时监测,若其有增大的趋势,则判断系统失稳,以此作为系统紧急控制的启动条件。图3分别为暂态失稳和暂态稳定时的相平面运动轨迹。

图3 暂态失稳及稳定的相平面
不稳定系统离散形式的表达式为
由式(26)可以看出,该方法使用简单,计算量小,可以方便应用于两机群间的暂态功角稳定性判别。该方法的推导基于系统等值后的二机系统,其准确性依赖于对系统机组分群的合理性,由于在线实时分群方法有很多,发展已较成熟,可以满足准确性的要求[24-26],故该方法具有良好的应用前景。
3.2 整体控制流程
当根据相平面轨迹的发展趋势判断出系统将失去稳定时,立即采取切机控制措施,减小加速机群原动机的出力,以此保障暂态稳定。由于计算是基于WAMS测量数据,将系统进行分群并等效为二机系统进行的,理论计算与实际控制可能有出入,故基于实时信息计算出切机量并实施切机措施后,应当继续对系统的动态进行实时监控,若系统仍然有失稳的趋势,应当利用当前的量测值开始新一轮的切机措施,重复此步骤,直至系统完全恢复稳定。具体控制策略表示如下:
a) 在监测到大扰动出现在系统中时,迅速启动以下控制流程。
b) 读入当前时刻的功角、角速度等实测数据,对系统进行等值,利用相平面的运动轨迹判断系统暂态稳定性,若判断出系统失稳,继续以下步骤。
c) 根据系统等值后的数据,预测得到功率曲线,计算当前未消纳的加速面积及满足稳定条件需要增加的减速面积。
d) 计算考虑惯性时间常数变化的所需切机量。
e) 实施切机控制,转入步骤b),若判断出系统稳定,则停止,若系统仍失去稳定,则转入步骤c)继续进行下一轮的控制。
4 算例分析
4.1 算例选择
为了验证本文提出的暂态稳定控制措施,在新英格兰10机39节点系统上进行仿真验证,新英格兰系统接线图如图4所示,参见文献[27]。采用仿真软件PSASP,得到发电机的功角、角速度、机械功率和电磁功率随时间变化的数据,视为WAMS采集的数据进行仿真。
4.2故障一
故障设置为:0.1 s时母线26-27之间中点发生三相短路,0.3 s切除故障。

图4新英格兰39节点系统

当故障在0.3 s清除时,从图5(a)功角曲线可以看出,39号机组是滞后群,其余机组为超前群,系统功角分二群摆开,最终会失去稳定。进行双机等值,从图5(b)可以看出,系统在相平面上的运动轨迹在某点处开始发散,出现凹凸的变换,同样表明系统在该故障下失去稳定。实时监视系统的运行状态,如图5(c),相平面上的运动轨迹在0.36 s开始有增大趋势,说明此时因功角差增大而增大的电磁功率已经不能使系统保持稳定,因此决定采取切机措施。假设各个控制环节的延时时间共为0.1 s,则实际切机发生在在0.46 s。对系统进行等值,如图5(d)所示,进行计算得,,。根据本文计算切机量得MW,在加速机群31-38中按出力进行分配,切机比例为14.67%,图6所示为切机后的系统功角曲线,系统恢复功角稳定,显示本文的切机控制方案控制有效。

图6 故障一切机后的功角曲线
4.3 故障二
设置故障为:17和母线27之间线路在0.05 s时发生三相短路故障,0.25 s断开线路切除故障。图7为该故障下相关曲线。
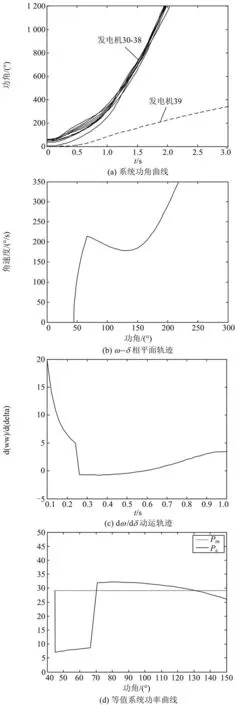
图7故障情况二的相关曲线
由图7(a)可以看出系统在该故障下失去稳定,其中加速机群为发电机30-38。根据图7(b)判断在0.34 s时系统等效的出现了增大的趋势,故以此时刻作为判定系统可能失稳的时刻,采取切机措施。考虑控制的总延时,设为0.1 s,故实际切机发生在0.44 s。求得,,。按文献[15]的方法求得切机量为=190 0 MW,在加速发电机群31-38实施切机措施,切机比例为37.38%,切机后机组的功角曲线如图8所示,可知系统在控制后仍然处于功角失稳的状态,该控制措施并不能使系统恢复同步运行,还可能错失最佳控制时机。

图8 故障二切机后的功角曲线
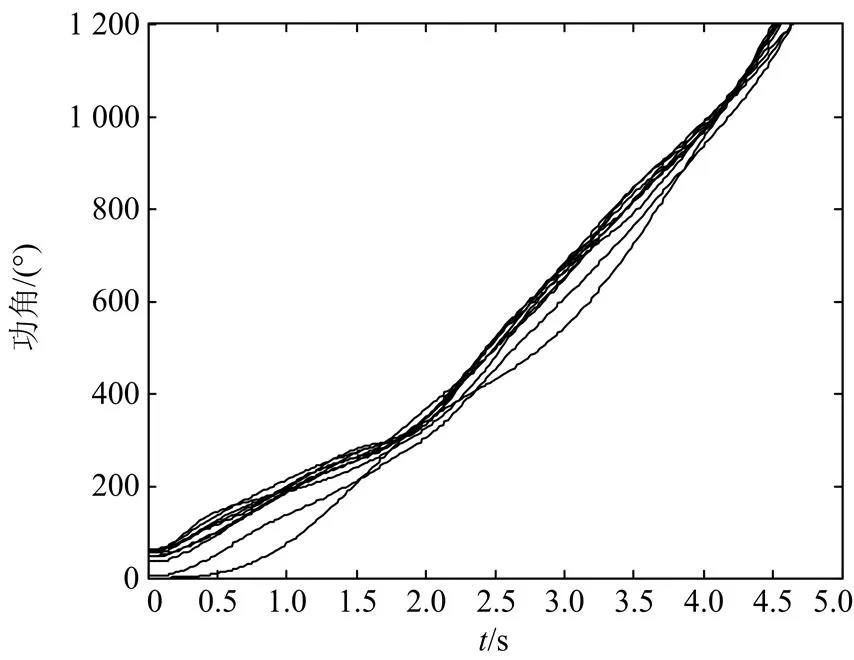
图9故障二切机后的功角曲线
4.4 仿真结果分析
由故障一的仿真结果可知,通过本文的紧急控制措施,可以有效使即将发生失稳的系统恢复稳定。通过故障二可以看出,由于在切机过程中系统的惯性时间常数不可避免会发生改变,而直接对系统的暂态过程造成影响,所以考虑惯性时间常数变化对切机量的影响是必要的,在某些情况下,未考虑惯性时间常数变化求取的切机量会较实际所需切机量偏小,从而不能达到很好的控制效果,并且可能不能通过一次控制保障系统稳定,从而失去最佳的控制时机。值得说明的是,由于每台机组分配的切机量不一定是单台发电机的倍数,故可能机组内实际切除发电机数量多于理论计算量,但是这种偏差切机功率占总切机量比例较小,仍较未考虑惯性时间常数变化的切机控制有较大的优势。
本文暂态稳定控制方案所需数据为发电机功角、角速度、功率等实时的数据,WAMS测得的数据具有实时性和广域性,可以完成这些数据的在线辨识功能[28]。目前,国内主要电网中已经有超过1 000套同步相量测量装置投入运行[29]。WAMS主站得到的实时动态数据由高速通信网络以毫秒级的时间间隔上传,可以达到系统暂态稳定控制对实时性的要求[30]。在发生故障后,可以滚动地读取WAMS数据对系统进行监测和控制。
5 结论
为了更好地应对电力系统安全稳定事故,本文提出了一种针对电力系统暂态稳定的实时切机方案。利用转速差–功角差相平面轨迹趋势实时判断系统暂态稳定性,并作为启动后续紧急控制的条件;将多机系统进行单机等值,根据不平衡能量计算所需的切机量,该方案同时考虑了切机过程中惯性时间常数变化对系统暂态过程的影响,使切机量更加准确,从而达到更安全有效的控制效果。此方案本质上属于反馈控制,可以对传统的安全稳定控制系统进行补充,但本文未考虑切机对等值发电机暂态电抗的影响,这将是后续研究的关注点。通过算例验证,该方案可以对暂态功角失稳进行有效的控制。
[1] 宫璇. 多重扰动下大电网低频振荡预警体系的研究[D]. 武汉: 武汉大学, 2013.
GONG Xuan. Study on early warning system of powergrid's low-frequency oscillation withmultiple disturbances[D]. Wuhan: Wuhan University, 2013.
[2] 周晖, 付娅, 韩盟, 等. 基于粒子群算法的含大规模风电互联系统的负荷频率控制[J]. 电力系统保护与控制, 2014, 42(10): 1-7.
ZHOU Hui, FU Ya, HAN Meng, et al. Load frequency control of power systems with large scale of wind power integrated based on particle swarm algorithm[J]. Power System Protection and Control,2014, 42(10): 1-7.
[3] 吴焯军, 赵淳, 张伟忠, 等. 直流输电线路雷害现状与分析[J]. 高压电器, 2014, 50(5): 134-139.
WU Zhuojun, ZHAO Chun, ZHANG Weizhong, et al. analysis on lightning damage of DC transmission lines in China[J]. High Voltage Apparatus, 2014, 50(5): 134-139.
[4] 范文涛, 薛禹胜. 电力系统紧急控制[J]. 继电器, 1998, 26(3): 1-5.
FAN Wentao, XUE Yusheng. Power system emergency control[J]. Relay,1998, 26(3): 1-5.
[5] 杨剑梅, 苟霖, 马青, 等. 配电网故障研判搜索定位系统研究[J]. 电网与清洁能源, 2015, 31(8): 59-63.
YANG Jianmei, GOU Lin, MA Qing, et al. Research on distribution network fault analysis and search orientation system[J]. Power System and Clean Energy, 2015, 31(8): 59-63.
[6] 魏韡, 梅生伟, 张雪敏. 先进控制理论在电力系统中的应用综述及展望[J]. 电力系统保护与控制, 2013, 41(12): 143-153.
WEI Wei, MEI Shengwei, ZHANG Xuemin. Review of advanced control theory and application in power system[J].Power System Protection and Control, 2013, 41(12): 143-153.
[7] 任伟, 房大中, 陈家荣, 等. 大电网暂态稳定紧急控制下切机量快速估计算法[J]. 电网技术, 2008, 32(19): 10-15.
REN Wei, FANG Dazhong, CHEN Jiarong, et al.A fast algorithm to estimate generation capacity tripped by emergency control for transient stability of large power system[J]. Power System Technology, 2008, 32(19): 10-15.
[8] 徐天奇, 尹项根, 游大海, 等. 广域保护系统功能与可行结构分析[J]. 电力系统保护与控制, 2009, 37(3): 93-97.
XU Tianqi, YIN Xianggen, YOU Dahai, et al. Analysis on functionality and feasible structure of wide area protection system[J]. Power System Protection and Control,2009, 37(3): 93-97.
[9] 卢芳, 于继来, 李彧, 等. 基于临界机组对的暂态稳定紧急控制策略[J]. 电网技术, 2012, 36(10): 153-158.
LU Fang, YU Jilai, LI Yu, et al. Transient stability emergency control based on critical generator pairs[J]. Power System Technology,2012, 36(10): 153-158.
[10]杨濛濛, 郭雷, 王春华, 等. 基于改进支路暂态能量函数的风电并网暂态最优切机控制[J]. 电力系统保护与控制, 2014, 42(18): 72-77.
YANG Mengmeng, GUO Lei, WANG Chunhua, et al. Transient optimal tripping control of grid-connected wind farms based on advanced branch transient energy function[J].Power System Protection and Control, 2014, 42(18): 72-77.
[11]任伟, 房大中, 吴烈鑫, 等. 基于修正能量函数的广东电网最佳稳措控制算法[J]. 天津大学学报, 2007, 40(2): 184-189.
REN Wei, FANG Dazhong, WU Liexin, et al. Optimal emergency tripping and load shedding evaluation using CTEF approach on power system in Guangdong[J]. Journal of Tianjin University, 2007, 40(2): 184-189.
[12]傅书逷, 倪以信, 薛禹胜. 直接法稳定分析[M]. 北京:中国电力出版社, 1999.
[13]单渊达. 对应用暂态能量函数法分析电力系统暂态稳定性的评价[J]. 电力系统自动化, 2001, 21(11): 10-15.
SHAN Yuanda. Evaluation of the transient energy function methods for power system transient stability analysis[J]. Automation of Electric Power Systems, 2001, 21(11): 10-15.
[14]陈永红, 薛禹胜. 区域紧急控制的优化算法[J]. 中国电力, 2000, 33(1): 44-48.
CHEN Yonghong, XUE Yusheng. Optimal algorithm for regional emergency control[J]. Electric Power, 2000, 33(1): 44-48.
[15]顾卓远, 汤涌, 张健, 等. 基于相对动能的电力系统暂态稳定实时紧急控制方案[J]. 中国电机工程学报, 2014, 34(7): 1095-1102.
GU Zhuoyuan, TANG Yong, ZHANG Jian, et al. Real- time power system transient stability emergency control scheme based on the relative kinetic energy[J]. Proceedings of the CSEE, 2014, 34(7): 1095-1102.
[16]牟龙华, 姜斌, 童荣斌, 等. 微电网继电保护技术研究综述[J]. 电器与能效管理技术, 2014(7): 1-7.
MU Longhua, JIANG Bin, TONG Rongbin, et al. Overview on micro-grid relay protection[J]. Electrical & Energy Management Technology, 2014(7): 1-7.
[17]杨文辉, 毕天姝, 马强. 基于广域电压相角信息的输电断面快速识别方法[J]. 电力系统保护与控制, 2013, 41(24): 58-63.
YANG Wenhui, BI Tianshu, MA Qiang. A method for searching transmission section based on wide-area voltage phasors[J]. Power System Protection and Control, 2013, 41(24): 58-63.
[18]沈健, 周斌, 汪昀. 提升PMU动态测量性能的若干方法[J]. 电力系统保护与控制, 2015, 43(19): 89-94.
SHEN Jian, ZHOU Bin, WANG Yun. Methods for improvement of dynamic performance of PMU[J].Power System Protection and Control, 2015, 43(19): 89-94.
[19]程云峰, 张欣然, 陆超. 广域测量技术在电力系统中的应用研究进展[J]. 电力系统保护与控制, 2014, 42(4): 145-153.
CHENG Yunfeng, ZHANG Xinran, LU Chao. Research progress of the application of wide area measurement technology in power system[J]. Power System Protection and Control,2014, 42(4): 145-153.
[20]李光琦. 电力系统暂态分析[M]. 北京: 中国电力出版社, 1995: 201-234.
[21]任先成, 薛禹胜, 丁明. 低频低压切负荷的控制负效应及其机理[J]. 电力系统自动化, 2009, 33(10): 1-5, 53.
REN Xiancheng, XUE Yusheng, DING Ming.Negative control effects of UFLS and UVLS[J]. Automation of Electric Power Systems, 2009, 33(10): 1-5, 53.
[22]吴为, 汤涌, 孙华东, 等. 暂态稳定受扰轨迹预测的模型参数自适应研究[J]. 电网技术, 2013, 37(3): 827-834.
WU Wei, TANG Yong, SUN Huadong, et al. Research on self-adaption of model parameters for prediction of disturbed trajectories in transient stability analysis[J]. Power System Technology, 2013, 37(3): 827-834.
[23]岑炳成, 唐飞, 廖清芬, 等. 应用功角空间降维变换的相轨迹判别系统暂态稳定性[J]. 中国电机工程学报, 2015, 35(11): 2726-2734.
CEN Bingcheng, TANG Fei, LIAO Qingfen, et al. Transient stability detection using phase trajectory obtained by dimension reduction transform of power angles[J]. Proceedings of the CSEE, 2015, 35(11): 2726-2734.
[24]陈铭, 刘娆, 吕泉, 等. AGC机组分群控制策略[J]. 电网技术, 2013, 37(3): 868-873.
CHEN Ming, LIU Rao, LÜ Quan, et al.A grouping control strategy for AGC units[J]. Power System Technology,2013, 37(3): 868-873.
[25]张园园, 龚庆武, 陈道君, 等. 应用改进粒子群优化的模糊均值聚类算法的暂态稳定机组分群方法[J]. 电网技术, 2011, 35(9): 92-98.
ZHANG Yuanyuan, GONG Qingwu, CHEN Daojun, et al.A unit clustering approach used in transient stability analysis based on improved PSO-FCM algorithm[J].Power System Technology,2011, 35(9): 92-98.
[26]谭伟, 沈沉, 李颖, 等. 基于轨迹特征根的机组分群方法[J]. 电力系统自动化, 2010, 34(1): 8-14.
TAN Wei, SHEN Chen, LI Ying, et al. A generator groups identification method based on trajectory eigenvalues[J].Automation of Electric Power Systems,2010, 34(1): 8-14.
[27] RAMON G L F. Prediction and control of transient instability using wide area phasor measurements[D]. Canada: University of Manitoba, 2012.
[28]段刚, 严亚勤, 谢晓冬, 等. 广域相量测量技术发展现状与展望[J]. 电力系统自动化, 2015, 39(1): 73-80.
DUAN Gang, YAN Yaqin, XIE Xiaodong, et al. Development status quo and tendency of wide area phasor measuring technology[J]. Automation of Electric Power Systems, 2015, 39(1): 73-80.
[29]韩松, 何利铨, 邱国跃. WAMS 研究、建设与应用的新进展[J]. 电测与仪表, 2011, 48(4): 1-8.
HAN Song, HE Liquan, QIU Guoyue. New progresses in the research, deployment and application of WAMS[J]. Electrical Measurement and Instrumentation, 2011, 48(4): 1-8.
[30]安思成, 吴克河, 毕天姝, 等. 适用于广域测量系统的实时数据并发访问同步算法[J]. 中国电机工程学报, 2014, 34(19): 3226-3233.
AN Sicheng, WU Kehe, BI Tianshu, et al. Synchronization algorithm for real-time data concurrent access applicable to WAMS[J]. Proceedings of the CSEE, 2014, 34(19): 3226-3233.
(编辑 周金梅)
Generator tripping strategy based on transient energy of power system
WANG Jiali1, LIU Dichen1, LIAO Qingfen1, CEN Bingcheng1, LI Shun1, QI Xiaoman2
(1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China; 2. State Grid Electric Power Research Institute, SMEPC, Shanghai 200437, China)
In order to achieve a more accurate power system emergency control measures, this paper proposes a method for calculating the amount of generation tripping considers inertia time constant change and allocates in accelerating generators. The method is based on the equivalent relative kinetic energy in the double-machine system, it does not depend on the specific model and power system parameters, can achieve real-time control of the power system, and needs a small amount of calculation, which is convenient and flexible. Taking the change of system inertia time constant into account in the process of generation tripping, a more accurate generation tripping measure is achieved. Simulation on the New England 10-generator 39-bus system verifies the effectiveness and a certain practical engineering value of the proposed scheme.
transient stability; generation tripping; inertia time constant; real time control
10.7667/PSPC151512
2015-08-25;
2015-12-01
王佳丽(1993-),女,硕士研究生,主要研究方向为电力系统运行与控制;E-mail: jialiwang100@gmail.com
刘涤尘(1953-),男,博士,教授,博士生导师,主要研究方向为电力系统分析与控制、电力系统规划等;
廖清芬(1976-),女,通信作者,副教授,主要研究方向为电力系统运行与控制。E-mail: qfliao@whu.edu.cn
国家电网公司项目“多区域安控系统协调及在线诊断、辅助决策技术研发应用”

