替换电阻简化电路*
(石狮市第一中学 福建 泉州 362700)
替换电阻简化电路*
(石狮市第一中学福建 泉州362700)
摘 要:对于某些复杂电路,用串联或并联的两个电阻替换电路中的某个电阻,能有效地简化复杂电路,可简便计算等效电阻等有关问题.
关键词:替换电阻串联替换并联替换简化电路
等效替换是一种重要的物理方法.在解决某些复杂电路问题时,可将电路中的某个电阻用串联或并联的两个电阻来替换,能有效地简化复杂电路,计算等效电阻,从而方便地解决问题.
1串联替换
所谓串联替换,就是将如图1(a)所示的电阻R,用串联形式的两个电阻R1和R2来替换,且R=R1+R2,其中R1=mR,R2=(1-m)R,m是一个正的实数,如图1(b)所示.替换之后,a与b两端点间的电压等于各分段电压之和.

图1
【例1】在如图2所示电路中,R1=R4=R5=1 Ω,R2=R3=2 Ω,若a与b两端点间的电压为U,求a与b两端点间的等效电阻Rab及c与d两端点间的电压Ucd.
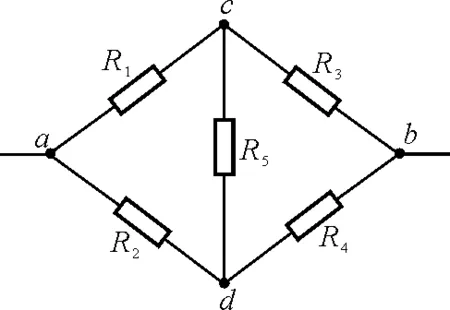
图2
解析:本题如果仅利用一般的电阻串、并联公式,不可能计算出Rab,若直接应用基尔霍夫定律则需要解多个冗长的一次方程组.
下面用替换电阻的方法来求解.
将电阻R2用两个电阻mR2和(1-m)R2串联的形式来替换,如图3.取c′为mR2和(1-m)R2的连接点,令c′点和c点电势相等.

图3
设电阻R1,R2,R3,R4,R5中的电流分别为I1,I2,I3,I4,I5,由于电路的对称性,可以看出
I1=I4I2=I3
由于
I1R1=mR2I2
I5R5=(1-m)R2I2
I2+I5=I4=I1
由此可得
解得
因而图1电路可等效为图4电路,通过串、并联计算求出

图4
或者,不仅将电阻R2替换为两个电阻mR2和(1-m)R2串联的形式,同时也将电阻R3替换为两个电阻mR3和(1-m)R3串联的形式,这样图1电路可等效为图5的电路,通过串、并联计算可求出

图5
2并联替换
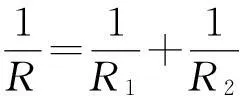



图6
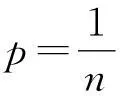

图7
在上面例1的解答中应用串联替换法,将单个电阻R2(以及R3)替换为两个电阻串联的形式.下面用两种不同的并联替换的方法解答例1.
解法1:在图2电路中,设电阻R1,R2,R3,R4,R5中的电流分别为I1,I2,I3,I4,I5,由于电路的对称性,可以看出
I1=I4I2=I3
因为I1=I3+I5,如图8(a),将R1用并联的两个电阻R11,R12来替换,且R11,R12中各自流过的电流I11,I12满足:
I11=I5I12=I3

由I2=I3=I12和a与d间的电压,得出
I11(R11+R5)=I12R2
所以
代入电阻具体数值,得
n=3R11=3 ΩR12=1.5 Ω
于是,图2电路可简化为等效的图8(b)电路.
或者,由于对称性,将R1用并联的两个电阻
R11=3 Ω、R12=1.5 Ω替换的同时,将R4也用并联的两个电阻R41=3 Ω,R42=1.5 Ω来替换,这样图2电路也可等效为图8(c)电路.
由图8(b)或图8(c),经过串、并联计算,可得
Rab=1.4 Ω

图8
解法2:根据I1=I4,I2=I3,将R5看成是由通有电流I1的R51和通有电流I2的R52的两个电阻并联而成,如图9所示.因为电流I1与电流I2的流向相反,于是n<1.

图9
I1R51+I2R52=0
I1(R1+R4+R51)=I2(R2+R3+R52)
代入电阻具体数值,得
3替换电阻方法的应用
3.1处理任意惠斯通电桥问题
【例2】如图10所示的惠斯通电桥,电阻R1,R2,R3,R4,R5的具体阻值未知,若流入a端点的电流为I0,求流过电阻R1,R2,R3,R4,R5中的电流.

图10



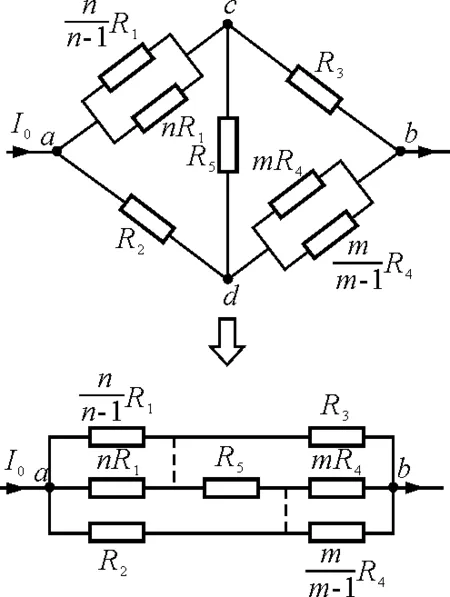
图11
由于
I5(nR1+R5)=I2R2
I5(R5+mR4)=I3R3
I1+I2=I0
所以
I0=nI5+(m-1)I5
即
因为
或
mR2-nR1=R5-R2
nR3-mR4=R5+R3
故
当求出m和n,就可知通过所有电阻的相应电流值
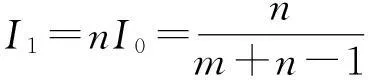


显然,m=n=∞,相当于一个平衡电桥.
因此
R2R3-R1R4=0
或
3.2简化框架类电路
【例3】如图12所示,立方体框架由12根相同的金属丝连接而成,每根金属丝的电阻为r.若电流从A点流入,从B点流出.求A与B点间的等效电阻.

图12
解析:由于电路的对称性,可用I1,I2和I3表示出每根金属丝中的电流,如图13所示.

图13

即m=2.



图14
A与B两点间的电压为
整理得
解得
n=5
于是
根据图14电路,通过串、并联计算可得
陈龙法**福建省教育科学“十二五”规划2015年度常规课题“高中物理教材二次开发案例研究”,项目编号:FJJK15-454作者简介:陈龙法(1961-),男,中学高级教师,主要从事高中物理教学与研究.
(收稿日期:2015-12-04)

