一种改进的基于遗传算法的测试调度方法

刘　伟，李　斌

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)



一种改进的基于遗传算法的测试调度方法

刘伟，李斌

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

摘要：提出了一种改进的基于遗传算法的SoC测试调度方法，通过该方法可以有效地优化测试总线的划分，合理调度各个IP核以实现并发测试，能够有效地缩短芯核测试时间。该算法把测试调度问题的可行解集用种群表示，逐代演化产生出越来越好的近似解。详细分析了该算法过程，对2002年国际测试会议(ITC’02)所提供的SoC国际基准电路进行测试调度实验，实验结果表明，此算法比传统的整数线性规划(ILP)和遗传算法的结果要好。

关键词：遗传算法；SoC测试；测试调度

0引言

随着半导体工艺技术的发展，IC设计者越来越倾向于使用内嵌的IP(intellectual property)核设计系统级芯片(system on chip,SoC)。这很大程度地缩短了产品进入市场的时间，同时也给SoC的测试带来很多新的挑战。通常，在一个SoC芯片上有几十个IP核，因此，为了减少测试时间，降低测试成本，如何分配测试资源和安排各个IP核的测试顺序成为一个很重要的问题。很多研究人员在测试调度方面做了很多工作。K.Chakrabarty把测试调度问题看成线性规划问题使测试时间最小化[1-3]。Lei Jia等提出了一种用遗传算法(genetic algorithm,GA)解决测试调度问题的方法[4]。

本文基于对传统遗传算法的分析，提出了一种改进的遗传算法，问题的解通过序列对表示。

1SoC测试优化问题划分

在IEEE1500标准中，提出了一种基于测试外壳(Wrapper)的测试结构。测试外壳是一个连接芯核与TAM的接口，提供对芯核的常规功能存取和通过TAM对芯核进行测试数据的存取。为了有效解决Wrapper和TAM之间的组合优化，按照复杂度的不同，V.Iyengar等人将这种组合优化问题划分为PW、PAW、PPAW和PNPAW[1]4个问题：

① PW问题：对给定的IP核设计测试外壳，使得这个核的测试时间和TAM宽度最小。

② PAW问题：给定NC个IP核和B条测试总线，每条测试总线的宽度分别为ω1，ω2，…，ωn，B条测试总线的总宽度为W，确定一种最优的组合将每一个核连接到各组测试总线上，使得SoC总的测试时间最少。

③ PPAW问题：给定NC个IP核，测试总线的总宽度为W，需要将W条测试总线划分为B组，将每一个核连接到各组测试总线上,使得芯片的总测试时间最少。PAW问题与PPAW问题的区别是PAW问题给定了每条测试总线的宽度，而PPAW问题要自己划分每条测试总线的宽度。

④ PNPAW问题：只给定了NC个IP核和测试总线的总宽度为W，需要确定总线划分成多少组，每组测试总线的宽度是多少，使得将每一个核连接到各组测试总线上使得芯片的总测试时间最少。

PW问题与背包问题类似，用BFD启发式算法可以比较好地解决[1,5]，对于PAW、PPAW和PNPAW问题，可以映射为整数线性规划(ILP)问题[2,3,6]；也可以映射为平面规划问题并结合各种启发类算法解决，本文重点研究PPAW问题。

2SoC 的测试调度

给定NC个IP核和测试总线的总宽度为W，则每个IP核Ci(1iNC)的测试配置可以用一个数组(Wij,T(Wij))表示，Wij表示第j组测试总线上IP核Ci的测试总线宽度，T(Wij)表示对应的测试时间。SoC测试调度的目标是决定每个IP核的测试开始时间和结束时间,以使总的测试时间最小。

这个问题可以映射为平面规划问题[7]，平面的高表示固定的总线宽度W，平面的宽表示总的SoC的测试时间。这时每个IP核的测试可以用一个高为Wij，宽为T(Wij)的矩形表示。目标就变为对每个IP核Ci设计一个矩形，并把所有的矩形都放在平面内，以使在总的高度不超过W的情况下总的宽度最小。且此时平面中的矩形不能相互重叠，因为任一测试总线在同一时间只能连接一个IP核。SoC测试调度问题转变为平面规划问题示意图如图1所示。

图1　平面规划问题示意图

3用遗传算法解决SoC的测试调度问题

3.1序列对结构

序列对结构是一种表示平面规划问题中矩形相对位置的十分有效的方法[8]。因为SoC的测试调度问题能够映射为平面规划问题，所以也可以用序列对来描述SoC的测试调度。

一组矩形的序列对(T+,T-)是2个序列，每个序列都包含所有的矩形。例如，(a b c ,c b a)是矩形a，b和c的一个序列对。序列对中矩形的相对位置可以通过下面2个规则确定。

规则1：序列对形式为(…a…b…，…a…b…)时，a在b的左边。

规则2：序列对形式为(…b…a…，…a…b…)时，a在b的下边。

给定一个序列对，根据序列对(T+,T-)中序列的顺序画斜线构建网格结构，则所有矩形分布在具有相同坐标的网线的交点处，序列对(a b c d e,d b e a c)对应的网格结构如图2所示。

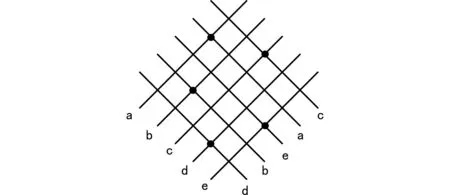
图2　序列对网格结构

每个序列对对应2个加权连接图，水平连接图和垂直连接图。这2个图可以由网格中的顶点位置确定。在水平连接图Gh中，当且仅当a在b的左边时，存在一条由a到b的连线；在垂直连接图Gv中，当且仅当a在b下面时，存在一条由a指向b的连线；此外每个连接图中都存在源节点和宿节点。水平连接图Gh中连接线的权重代表对应矩形的宽，垂直连接图Gv中连接线的权重代表对应矩形的高。所以，Gh和Gv中最长路径的长度分别代表平面规划的宽和高。也就是SoC测试调度问题中总的测试时间和测试总线带宽。序列对(a b c d e,d b e a c)的水平连接图Gh和垂直连接图Gv如图3和图4所示。

图3　水平连接图Gh

图4　垂直连接图Gv

3.2遗传算法

遗传算法是从代表问题可能潜在解集的一个种群开始，按照适者生存、优胜劣汰的原理，逐渐进化产生近似最优解[9]。在每一代中，根据个体适应度大小进行筛选，并借助自然遗传学的遗传算子进行交叉组合和变异，生成代表新的解集的种群。这个过程使种群像自然进化一样越来越适应环境，其对应的解也越来越接近最优解[10-12]。最后，末代种群的最优个体经过解码，可作为问题的近似最优解。

遗传算法包括选择、交叉和变异3种基本操作，遗传算法的基本流程图如图5[13]所示。

图5　遗传算法流程图

遗传算法的结果由序列对表示，目标是在总线宽度不超过Wmax的情况下，使测试时间最小化。传统遗传算法的伪代码为：

① 设置适应度C为水平连接图Gh中最长路径的长度；限制条件为Gv≤Wmax;

② 设置Gen=0,随机产生可能解的初始种群；

③ 计算每个解的适应度C；

④ 通过2个初始解的交叉组合产生2个子代Ⅰ和Ⅱ；

⑤ 通过对子代Ⅰ和Ⅱ进行变异操作产生2个子代Ⅲ和Ⅳ，选择4个中最好的2个解作为下一代；

⑥ 计算当前种群的解，选出最优方案；

⑦Gen=Gen+1，如果Gen<1 000，进入第④步；

⑧ 得出最优解；

⑨ 结束。

对于交叉组合操作，选择2个序列对，随机选择一个位置l(1≤l≤Nc)，交换2个序列对T+中l位置的IP核和对应T-位置的IP核。例如，在序列对Ⅰ的T+中，l位置对应的IP核为P，在序列对Ⅱ中l位置对应的IP核为Q。交叉组合操作就会交换P和Q在T+和T-中的位置。

变异操作通过下面几种方法施行，每个方法使用的概率分别为0.3,0.1,0.2,0.2,0.2。

① 交换T+中2个相邻IP核的位置；

② 在T-中随机选择2个IP核，交换它们的位置；

③ 在T+中随机选择连个位置，颠倒2个位置之间的IP核的顺序；

④ 随机选择一个IP核，在T+中随机选择一个位置插入。

⑤ 改变矩形的宽和高。

分析算法可以发现，在产生后代的过程中，是通过对子代适应度的排序，选择适应度最好的2个进入下一代母本，在这个过程中，并没有把母本的方案考虑进去，也就是说，子代方案不一定比上一代好，即下一代方案测试时间不一定比上一代更少。

针对以上情况，提出一种改进的遗传算法(improved genetic algorithm,IGA)，伪代码如下：

① 设置代价函数C为水平连接图Gh中最长路径的长度；限制条件为Gv≤Wmax;

② 设置Gen=0,随机产生可能解的初始种群；

③ 计算每个解的适应度C；

④ 通过2个初始解的交叉组合产生2个子代Ⅰ和Ⅱ；

⑤ 通过对子代Ⅰ和Ⅱ进行变异操作产生2个子代Ⅲ和Ⅳ，计算母代与4个子代的适应度，选择最好的2个解作为下一代；

⑥ 计算当前种群的解，选出最优方案；

⑦Gen=Gen+1，如果Gen<1 000，进入第④步；

⑧ 得出最优解；

⑨ 结束。

在选择下一代的过程中，通过把母本方案考虑进去，保证了下一代的适应度比上一代更好，即测试时间更少，因此算法在理论上可以得到更好的近似最优解，使测试时间更短。当然，算法的复杂度也略有增加。本算法以50个随机产生的父母作为初始种群，每一个父母对应一个序列对。通过上述的交叉组合，变异和选择产生后代种群。

4实验结果

采用ITC’02所提供的SoC测试基准电路d695作为实验电路。用C语言实现了遗传算法程序，同时也实现了文献[1]所描述的ILP(integer linear programming)算法，最后得到的测试时间如表1所示。从表1可以看出，GA算法的测试周期几乎都小于ILP算法的测试周期，而IGA算法的测试周期又比以上2种算法小。

表1　基准电路OTC’02(D695)上的实验结果

5结束语

通过研究Wrapper/TAM组合优化算法，提出了一种改进的遗传算法解决SoC的测试调度问题。测试调度问题被映射成平面规划问题，并通过序列对表示，然后用遗传算法寻找最优解。实验结果表明，算法的测试周期比ILP算法和传统遗传算法的测试周期要少。所以，此改进的遗传算法在减少SoC测试时间上是有效的。

参考文献

[1]Iyengar V,Chakrabarty K,Marinisen J.Test Wrapper and Test Access Mechanism Co-Optimization for System-on-chip[C]∥J.Electronic Testing:Theory and Applicaton,2002:213-230.

[2]Chakrabarty K.Design of System on Chip Test Access Architectures Using Integer Programming[C]∥Proc.VLSI Symposium,2000:127-134.

[3]Chakrabarty K.Test Scheduling for Core-based Systems Using Mixed-integer Linear Programming[J].IEEE Trans.CAD,2000,19(10):1163-1174.

[4]雷加,方刚.一种基于遗传算法的SoC测试调度方法[J].仪器仪表学报,2007,28(4):15-17.

[5]Garey M R,Johnson D S.Computers and Intractability-a Guide to the Theory of NP-completeness[M].San Francisco:W.H.Freeman and company,1980:221-281.

[6]Papachristou N C.An ILP Formulation to Optimize Test Access Mechanism in System-on-chip Testing[C]∥Proc.Int.Test conf,2000:902-910.

[7]邓立宝,俞洋,彭喜元.一种灵活TAM总线分配的SoC测试调度方法[J].仪器仪表学报，2011,32(6):1238-1240.

[8]Murata H,Fujiyoshi K,Nakatake S,et al.VLSI Module Placement Based on Rectangle-packing by the Sequence-pair[C]∥IEEE Trans.on Computer-Aided Design,1996:1518-1524.

[9]张旺,王黎莉,伍洋.基于遗传算法的阵列天线综合及分析[J].无线电通信技术,2011,37(4):28-30.

[10]周磊,李大鹏,朱峰.基于遗传算法的多侦查传感器目标优化分配[J].无线电工程,2012,42(6):55-57.

[11]谈敏,蔡钧.基于改进遗传算法的双频滤波器自动设计[J].无线电工程,2012,42(10):48-50.

[12]高朝晖,岳群彬,李伟.遗传算法在成像卫星计划编制中的应用[J].无线电工程,2013,43(12):37-40,60.

[13]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安：西安交通大学出版社,2002.

An Improved Test Scheduling Method of SoC Based on Genetic Algorithm

LIU Wei ,LI Bin

(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)

Abstract：This paper proposes an improved SoC test scheduling method based on genetic algorithm,which can efficiently optimize the division of testing bus,reasonably schedule each core to realize parallel test,and efficiently shorten the test time of core.Representing feasible solution of test scheduling with population,based on “survival of the fitness”,and beginning with the initial population,this algorithm evolves by generation to produce approximation solution.Utilizing international reference circuit provided by International Test Conference 2002 (ITC’02),we execute the test scheduling experiment.And the results suggest that this algorithm be superior to conventional integer linear programming (ILP) algorithm and conventional genetic algorithm.

Key words：genetic algorithm; test scheduling; optimization test

中图分类号：TP18

文献标识码：A

文章编号：1003-3114(2016)02-37-4

作者简介：刘伟(1989—)，男，硕士研究生,主要研究方向：数字集成电路设计。李斌(1972—)，男，研究员,主要研究方向：集成电路设计。

基金项目：核高基重大专项(2009ZX01031-001-007)

收稿日期：2015-11-10

doi:10.3969/j.issn.1003-3114.2016.02.09

引用格式：刘伟，李斌.一种改进的基于遗传算法的测试调度方法[J].无线电通信技术,2016,42(2):37-40.