多波束卫星移动通信系统的同频干扰研究

尹　展，孙晨华

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)



多波束卫星移动通信系统的同频干扰研究

尹展，孙晨华

(中国电子科技集团公司第五十四研究所，河北 石家庄050081)

摘要：针对多波束卫星移动通信系统的特点，分析了多波束卫星移动通信系统与地面蜂窝系统同频干扰计算方法的差异性，考虑了接收终端和波束中心卫星天线方向夹角带来的增益量的衰减，提出了适用于该系统的同频干扰算法，建立了适合于本系统的同频干扰分析模型。计算得到的载干比可以作为资源规划的反馈参考，为资源规划做出指导，满足更高的通信质量要求。

关键词：同频干扰；频率复用；多波束；载波规划

0引言

目前，对于地面蜂窝系统同频干扰的探讨已经相对成熟，但是针对多波束卫星移动通信系统同频干扰的研究还很匮乏。虽然多波束卫星移动通信系统与地面蜂窝系统有很多相似之处，但是卫星系统的干扰情况与接收终端和波束中心到卫星天线方向夹角有关，而地面蜂窝系统只考虑了复用距离[1]，显然照搬地面蜂窝系统同频干扰算法是不可行的。

同频干扰是由于系统采用同频复用引起的，所谓同频复用就是指在相隔一定物理距离的2个波束内使用相同的频率，这样做大大提高了频谱的使用率，极大地扩充了通信网的容量，但同时也带来了相应的问题，相隔一定物理距离的波束内频率相同的载波相互干扰，给用户造成了很大的困扰[2]。

本文结合多波束卫星移动通信系统的特点，提出适用于该系统的同频干扰算法，提高了干扰计算的准确度和可信度。

1干扰分析模型

在考虑同频干扰时，终端接收信号的下行载干比(C/I)是一个重要的指标[3]。下面通过建立干扰分析模型来计算终端接收信号的下行载干比。

构建干扰分析模型的主要功能是确定每个波束内的载波后，计算波束内每条载波的同频干扰值，并据此判断该波束内载波配置是否满足载干比要求。

多波束卫星移动通信系统同频干扰分析方法与地面蜂窝系统同频干扰分析方法有些不同，主要体现在2个方面：① 多波束卫星移动通信系统中同频干扰的大小不与距离的幂次方成正比，而与接收终端和波束中心到卫星天线方向夹角密切相关；② 蜂窝系统每个小区有一个相同发射功率的基站作为中继[4-7]，多波束卫星通信系统中使用卫星作为中继，所以蜂窝系统中信号的传播路径是从小区中心基站到移动台[8]，而在多波束卫星移动通信系统中，信号的传播路径是由卫星发射天线到终端，并不是从波束中心到终端。

下面将通过3步来建立多波束卫星移动通信系统同频干扰分析模型：第①步，求解任意两点卫星天线方向夹角；第②步，建立任意波束的卫星天线方向图；第③步，求解同频干扰功率和载波功率。

1.1卫星天线方向夹角

由于在计算波束间的同频干扰时，同频干扰值的大小与路径传播衰减密切相关，而在多波束卫星移动通信系统中，路径传播损耗的大小不与传播距离的幂次方成正比，而是与接收终端和波束中心到卫星天线方向夹角有关系，所以首先要确定接收终端和波束中心之间的卫星天线方向夹角。

首先要已知接收终端、波束中心的经纬度和卫星的位置，然后建立以下模型分析接收终端和波束中心天线方向夹角。

如图1所示，假设卫星的位置为λ1E，由于研究的是GEO卫星，卫星星下点A的经纬度即为(λ1E，0)，假设波束中心B接收终端C的经纬度分别为(λ2E，φ2N)和(λ3E，φ3N)，星下点A与波束中心B的地心夹角为θ1，星下点A与接收终端C的地心夹角为θ2，波束中心和接收终端B、C的地心夹角为θ3，波束中心和接收终端的卫星天线方向夹角为α，地球的半径为R(km)，卫星的高度为H(km)。

图1　卫星天线方位夹角示意图

利用A、B两点经纬度可以得到A、B两点的地心夹角θ1，

同样，利用A、C两点经纬度可以得到A、C两点的地心夹角θ2，

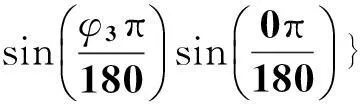
利用B、C两点经纬度可以得到B、C两点的地心夹角θ3，

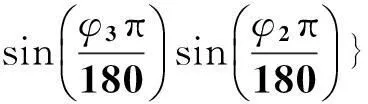
在三角形BOD中，已知BO长为R，DO长为H+R，得出BD长度，

在三角形COD中，已知CO长为R，DO长为H+R，得出CD长度，

在三角形BOC中，已知BO长为R，CO长为R，得出BC直线长度，

在已知三边长度之后，在三角形BCD中，可以得到BD与CD的夹角α，

因此，波束中心B与接收终端C的的卫星天线方向夹角为α。

1.2卫星天线方向图

卫星天线方向图是得到载波功率衰减的重要工具，下面简单利用天线原理的知识来阐述任意波束对应的抛物面卫星天线方向图的求解过程。

计算抛物面辐射场有2种方法——面电流法和口径场法，本文采用的是口径场法。抛物面口径，是由抛物面边缘限定的垂直于轴线的圆平面，在求抛物面口径场强分布时，要应用2条定量：一是几何光学反射定律，另一是能量守恒定律。

用口径场法计算的远区辐射场：

计算抛物面辐射场时，主要关系方向图主瓣和近副瓣，通常θ角不大，cosθ≈1[9]，而且仅计入口径场主极化分量，于是，抛物面天线辐射场：

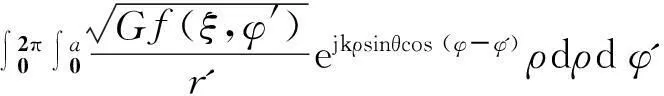
式中，Gf(ξ，φ')为馈源方向函数，当馈源方向图给定时，将式中的变量(ξ，r')变换成(ρ，φ')。根据抛物面的几何特性，从图2可得：

图2　半圆天线口径示意图

然后利用插值法，得到辐射场:

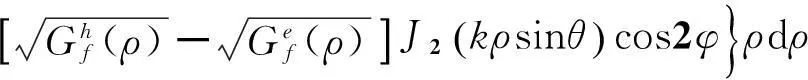
当馈源为圆形波导辐射器馈源时，焦径比为0.333的抛物面天线，从上式计算得出卫星天线方向图，归一化后如图3所示。

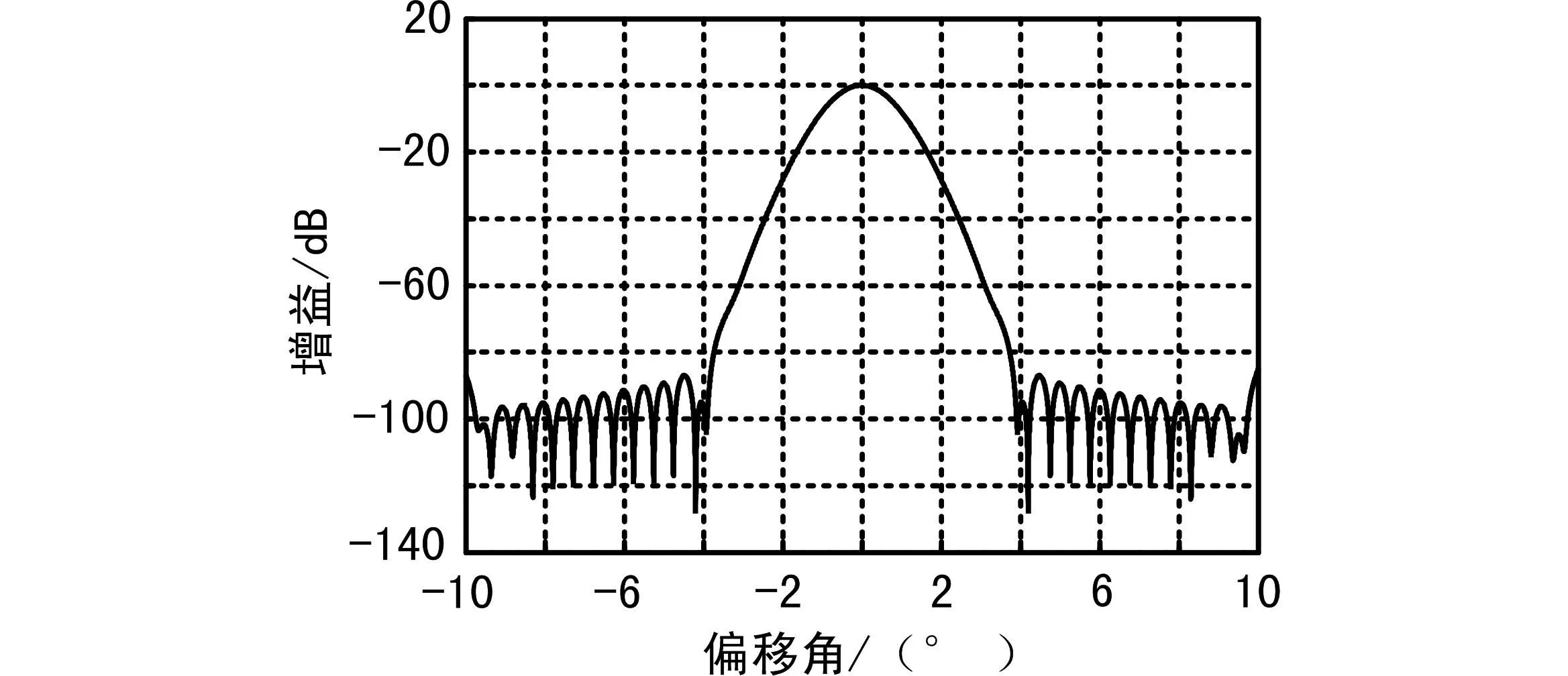
图3　抛物面卫星天线方向图

由图3可知，卫星天线方向夹角与天线增益并不是简单对应的角度越大(相距越远)增益越小，在主瓣和旁瓣变换或旁瓣间变换的时候增益在一定角度内反而会增大，这是与地面蜂窝系统最大的差异。

在得到一个波束的卫星天线方向图之后，可以认为卫星通信系统中所有波束的卫星天线方向图都相同[10]。

1.3干扰功率

在得到接收终端和波束中心卫星天线方向夹角与卫星天线方向图之后，接下来计算同频干扰功率，确定了终端类型和业务类型，用以下方式计算同频干扰的功率,多波束卫星同频干扰示意图如图4所示。

图4　多波束卫星同频干扰示意图

1.3.1计算载波下行EIRPdc

载波下行EIRPdc为：

EIRPdc=EIRPs-BOoc。

式中，EIRPs为卫星饱和EIRP，BOoc为每载波输出补偿，

BOoc=BOic+BOo-BOi。

式中，BOic为每载波输入补偿，BOo为转发器输出补偿，BOi为转发器输入补偿，

BOic=10lgV+BOi。

式中，V为系统容量。

因此，载波下行EIRPdc可表示为：

EIRPdc=EIRPs-10lgV-BOo。

1.3.2计算同频干扰功率

卫星发射信号落入本波束的载波功率为：

C=EIRPdc-LFD-La，

式中，LFD为下行自由空间传播损耗，La为大气吸收损耗。

根据卫星波束复用关系、卫星天线方向图和卫星天线方向夹角计算复用波束落入本波束的干扰功率Ii(i=1，2，…，M-1，M为波束复用的次数)。假设接收终端与复用波束中心之间的卫星天线方向夹角为αi(i=1，2，…，M-1)，αi对应的归一化后的卫星天线方向图中的衰减量为ωαi，那么复用波束i对应的同频干扰值为：

Ii=C-ωαi。

注：假如第i个复用波束中没有使用该频点的终端在工作，那么Ii=0。

那么总的同频干扰功率为：

至此，对某频点的载干比就可以用下式表示:

2评判标准

在计算得到波束中频点的载干比(C/I)之后，则需要一个评判标准来确定该载干比是否能够满足通信要求。载干比的计算是为了评判载波规划的结果是否能够满足卫星移动通信要求，如果载干比过低，即有用信号太小，干扰信号太大的情况下，则需要重新考虑载波规划。

首先，对于数字地面蜂窝系统的评判标准，我国的GSM系统、美国的IS-54系统和日本的PDC系统为了保证绝大多数地区和绝大部分时间的通信质量，都要求载干比不得<9 dB，即C/I≥9dB[11-13]。

考虑到卫星移动通信系统复杂的链路情况以及更高的通信要求，一般认为卫星移动通信系统中载干比不得小于13 dB，即C/I≥13dB[14,15]。

3仿真验证

仿真试验中载波分配完成后，得到波束1的前20个频点的载干比的情况如图5所示。

图5　波束1载干比(C/I)

从图5中可以看到，有些频点的C/I满足通信要求>13 dB，而某些频点的C/I不能满足>13 dB的要求，这就需要对规划结果进行调整，以使得该频点的载干比能满足通信要求，例如8号频点载干比明显<13 dB，则需要对8号频点进行调整。

4结束语

同频干扰是频率复用系统中不可忽视的一个问题，合理规划载波分配方案是解决同频干扰问题的重要手段，而同频干扰分析模型是评判载波规划方案优劣的重要依据。在分析了多波束卫星移动通信系统与地面蜂窝系统的区别之后，建立了适合于本系统的同频干扰分析模型，并在系统的载波规划方案确定后对每个频点的载干比进行了仿真，证明了干扰分析模型的正确性和有效性，这就为下一次的载波规划提供了指导和借鉴。

参考文献

[1]张业荣，竺南直，程勇．蜂窝移动通信网络规划与优化[M]．北京：电子工业出版社，2008．

[2]Liu Fang，Wang Ying，Zhang Ke．Spot Beam Handover Trigger and Channel Allocation Scheme in GEO Mobile Satellite Communication[J]．High Technology Letters，2011，17(2)：146-152．

[3]韩斌杰，杜新颜，张建斌．GSM原理及其网络优化[M]．北京：机械工业出版社，2008．

[4]柯文渊．GSM网络中同邻频干扰分析优化的方法研究与系统实现[D]．北京：北京邮电大学，2011：18-22．

[5]纪谢平,徐家品.基于中继抑制蜂窝网络同频网络干扰的方案[J].无线电工程,2015,45(4):20-24.

[6]王和,刘光斌,程俊仁,等.卫星导航接收机抗干扰测试评估方法研究[J].无线电工程,2014,44(3):5-7.

[7]陈强．卫星导航接收机的抗干扰技术分析[J]．无线电工程，2011，41(11):34-36,64．

[8]吴志彪．移动通信网络中无线资源管理技术的研究[D]．南京：东南大学，2006：21-25．

[9]魏文元，宫德明．天线原理[M]．北京：国防工业出版社，1985．

[10]Grandhi S A，Goodman D J．Resource Allocation for Cellular Radio Systems[J]．IEEE Trans．1997，46(3)：581-587．

[11]吴诗其，胡剑浩，吴晓文．卫星移动通信新技术[M]．北京：国防工业出版社，2001．

[12]陈振国．卫星通信系统与技术[M]．北京：北京邮电大学出版社，2003．

[13]郭梯云．移动通信[M]．西安：西安电子科技大学出版社，2000．

[14]汪春霆，张俊祥，潘申富，等．卫星通信系统[M]．北京：国防工业出版社，2012．

[15]杨巧丽，陆锐敏，马刈非．GEO多波束卫星通信网络关键技术研究[J]．通信技术，2009，5(42)：158-160.

Research of Co-frequency Interference in Multi-beam Satellite Mobile Communication System

YIN Zhan,SUN Chen-hua

(The 54th Research Institute of CETC,Shijiazhuang Hebei 050081,China)

Abstract：Based on the characteristics of multi-beam satellite mobile communication system,the paper analyzes the difference between theco-frequency interference calculation methods of multi-beam satellite mobile communication system and cellular system.The gain attenuation brought by the angle formed by the receiving terminal and the beam center with the satellite antenna is taken into account.A co-frequency interference algorithm and aco-frequency interference analysis model adapted to the satellite system are introduced.The carrier-to-interference ratio can be used as a reference of carrier optimization to satisfy higher requirement of communication quality.

Key words：co-frequency interference; frequency reuse; multi-beam; carrier planning

中图分类号：TN927

文献标识码：A

文章编号：1003-3114(2016)02-23-4

作者简介：尹展(1990—)，男，硕士研究生,主要研究方向：卫星移动通信。孙晨华(1964—)，女，研究员，主要研究方向：卫星通信系统及总体技术。

收稿日期：2016-11-03 国家部委基金资助项目

doi:10.3969/j.issn.1003-3114.2016.02.06

引用格式：尹展，孙晨华.多波束卫星移动通信系统的同频干扰研究[J].无线电通信技术,2016,42(2):23-26