振动台非线性破坏模型试验影响因素*

李 静， 陈健云， 徐 强， 郑 毅

(大连理工大学建设工程学部 大连，116024)

振动台非线性破坏模型试验影响因素*

李 静， 陈健云， 徐 强， 郑 毅

(大连理工大学建设工程学部 大连，116024)

振动台模型试验是研究工程结构的动力特性和抗震性能的重要手段，针对振动台模型破坏试验中地震动加载方式及材料模型等影响因素进行了研究。分别采用大体积水工混凝土结构和框架结构对一次性强震作用与地震动逐级累积作用下结构损伤差异进行了对比分析。结果表明，对于大体积脆性混凝土结构及框架结构，逐级加载方案及仿真材料模量和强度的相似性均能够保证结构的线弹性动力特性、损伤起始加速度及极限抗震能力的试验要求，但是不能反应结构从损伤发生到失效破坏的中间发展过程。在进行振动台模型试验时，可根据具体试验目的选择相应的简化措施。

模型试验； 结构损伤； 地震动； 数值仿真； 振动台

引 言

随着我国经济实力的提高，大坝和桥梁等一批重大工程在西部高烈度地震区得到建设，对于这些结构，其抗震安全成为工程的控制性因素[1]。结构抗震性能及破坏形态可以通过实际震害、理论分析、数值计算以及振动台模型试验等手段进行研究。西部山区工程地质地形复杂，环境恶劣，结构抗震分析和数值计算模型，材料参数等均存在不确定因素，振动台模型试验成为校核数值分析模型、了解结构破坏形态以及抗震安全按评价的重要手段[2]。目前，对于300m级的高混凝土坝直接遭受震害破坏的案例极少，对其在强震作用时的破坏过程和破坏形式等还缺乏了解，因此振动台模型破坏试验就成为重大工程抗震安全评估的必要环节和手段[3]。

通过振动台模型试验进行结构强震破坏模式和安全校核的研究时，通常事先确定地震动加速度幅值[4]。不同于一般工民建结构的抗震试验，水工高坝重大工程结构往往通过振动台试验研究其失效破坏模式和极限抗震能力，结构破坏时的加速度往往作为大坝安全评估的重要参考[5]，而当前非线性动力破坏试验还还存在较多问题。根据结构模型动力试验的相似理论，模型非线性动力试验设计的主要困难在于选择满足动力非线性相似要求的模型材料和试验技术[6]。由于结构承受极限加速度的能力是未知的，以及模型制作周期和试验成本的限制，极限抗震能力的振动台模型试验往往通过地震动的逐级加载来进行[7]。但是，结构的损伤破坏是一个逐渐累积的过程，结构在逐级加载下指导破坏的损伤累积过程与结构破坏加速度一次性直接作用下的损伤累积过程是有差别的。在结构进入非线性状态后，逐级加载过程实质上相当于增加了地震动的有效持时。同时，非线性相似理论要求以下相似条件要求[8]：内力-重力-惯性力-面力相似、应力-应变曲线相似、累计损伤曲线相似以及断裂特性相似。实际上现有的模型材料很难完全满足以上所有相似要求。因此，通常根据试验目的和结构破坏机理，放宽一些限制条件而采取一些近似方法[9]。影响结构动力破坏的因素很多，需要满足的独立相似要求更多[10]，一些在线弹性模型试验中不需考虑的因素在非线性试验中可能影响很大，比如模型材料的强度和峰值后特征等。

笔者针对这一问题，根据大坝这类大体积素混凝土结构的脆性破坏特征，分析了不同加载方案的影响，通过非线性数值分析对比了忽略材料峰值后特征的影响；并通过框架结构算例阐述了不同加载方案对不同损伤破坏阶段的影响规律，进一步论证了地震动加载方式对结构损伤的影响。

1 大体积混凝土结构振动台破坏试验的数值仿真分析

1.1 动力破坏试验仿真模型

根据结构动力方程，可以得到

(1)

其中：Ct，Cρ，Cσ，Cl和CE分别为原型/模型的时间比尺、密度比尺、应力比尺、几何比尺及模量比尺。

对于线弹性模型，可以选择3个独立变量作为3个基本变量，比如Cρ，Cl和CE，其他相似比尺均可根据3个基本量求得。若进行非线性损伤破坏过程试验研究，上述相似比尺之间的关系依然成立，但同时要求原型与模型的应力-应变关系完全相似，也就是满足弹性-重力相似率[9]。对于大体积素混凝土结构，主要破坏机理为受拉开裂，因此可以将要求降低为模量和抗拉强度的弹脆性相似性。

材料非线性动力模型试验各物理量完全相似比尺关系[10]如表1所示。

表1 非线性动力相似准则

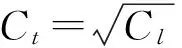
1.2 计算模型和计算条件

有限元模型如图1所示，采用混凝土单元、线弹性本构模型和W-W五参数破坏准则，不考虑压碎。模拟5条横缝，动力抗拉强度取2.6 MPa。地基范围为从坝体向下取2倍坝高，向上、下游及两侧取1.5倍坝高。仿真模型有限元网格同原型，单元大小根据模型几何比尺确定，模量及强度参数根据相似比确定，满足强度比尺。

计算中考虑正常蓄水位下的静水压力、动水压力和地震荷载。动水压力采用Westergaard动水压力公式计算。地震动水平输入，地震波为根据水工抗震规范地震反应谱造波得到的人工波，如图2所示，模型地震波时程波形与原型一致，时间缩尺为1/10。对模型结构按照峰值加速度分别为0.1, 0.2, 0.3, 0.4, 0.5及0.6g逐级加载进行分析，并将结果按照比尺换算到原型，分别与0.1,0.3,0.5和0.6g地震动作用下的原型结构损伤结果以及地震动持时延长的地震动损伤结果进行比较(峰值持时延长一倍的地震动时程如图3所示)。

图1 拱坝的有限元模型Fig.1 The finite element model of arch dam

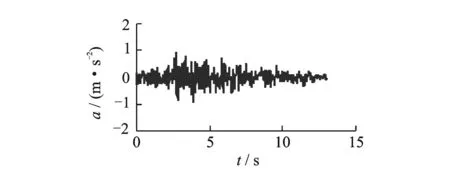
图2 人工地震波(原型)Fig.2 Artificial earthquake

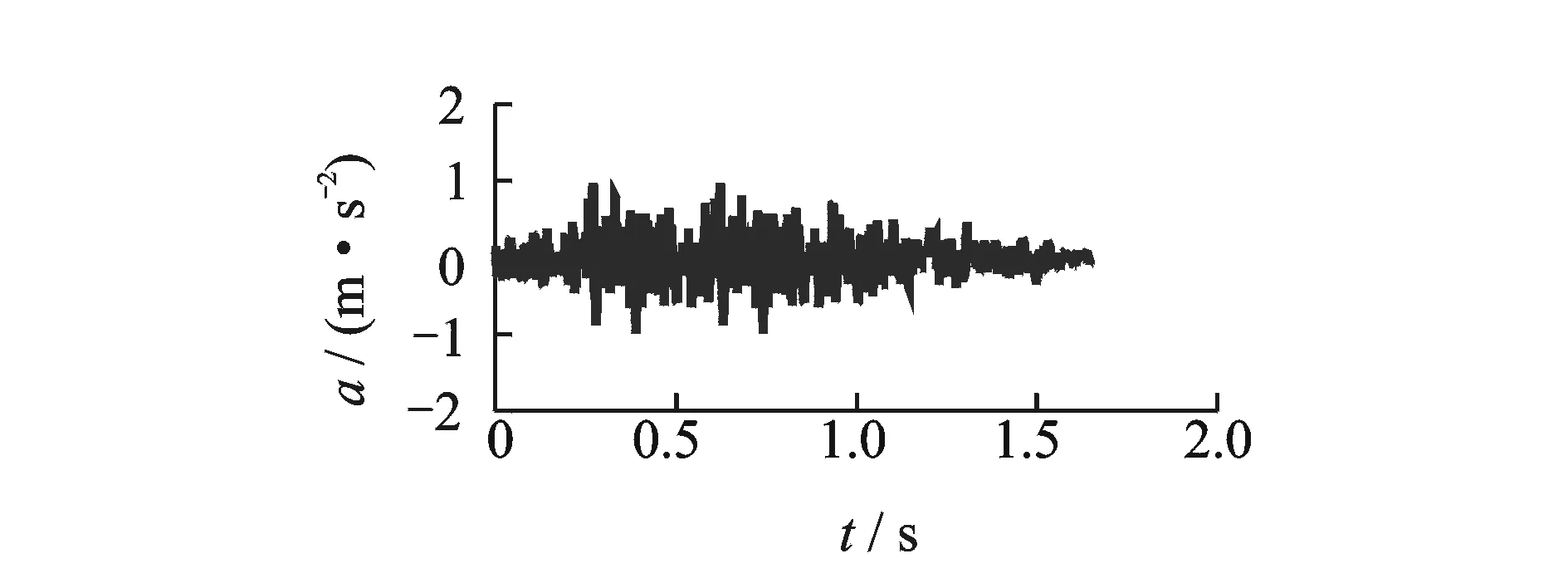
图3 持时延长后的地震波(缩尺)Fig.3 Extended duration earthquake

1.3 计算结果

通过将模型分析结果按照相似比尺换算到原型后，与按照原型材料计算得到的分析结果进行比较，0.1g和0.3g地震动峰值加速度下坝面没有出现损伤，坝体动力响应完全相同，与持时延长地震动作用下的坝体动力响应特性也相同。在0.5g峰值加速度作用下，结构已经出现损伤，但是模型与原型在损伤分布和损伤程度上都不相同。增大到0.6g情况下，原型结构上游面拱冠梁附近出现损伤，与模型结构坝面损伤部位已经基本相同，下游面则模型结构坝趾部位出现损伤，原型还没有出现，继续增大加速度后出现与模型损伤分布相同。地震动持时延长时，0.5g地震加速度作用下模型结构上、下游面损伤部位就已经与原型极限承载能力下的情况相同，0.6g峰值加速度下损伤部位不再变化，只是损伤程度有所增加。0.6g峰值加速度作用下的坝面损伤分布如图4所示。持时延长地震动下坝面损伤结果如图5所示。模型和原型逐级动力加载分析得到的拱冠位移与峰值加速度关系如图6所示。

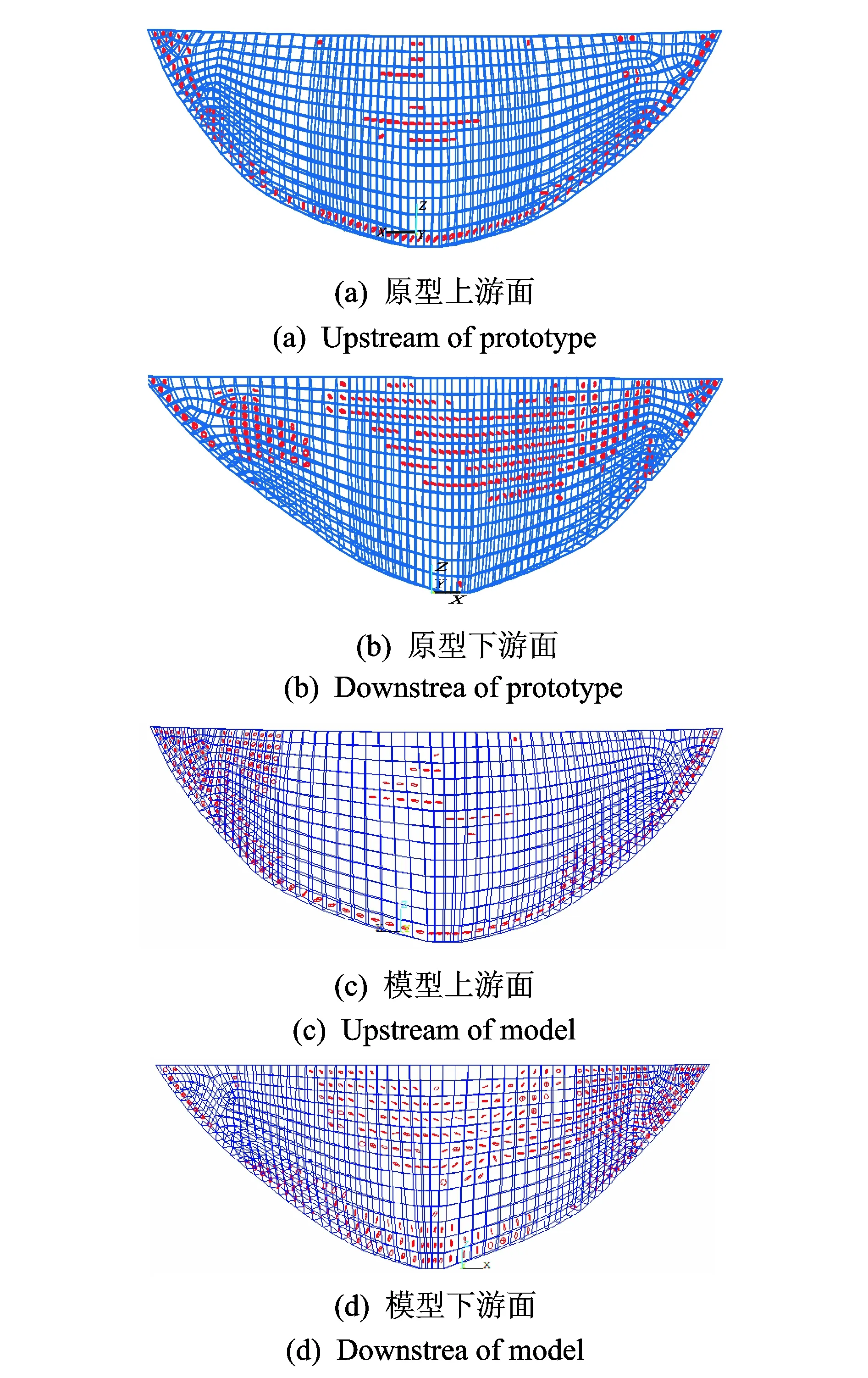
图4 拱坝损伤分布(0.6g)Fig.4 Damage distribution of arch dam(0.6g)

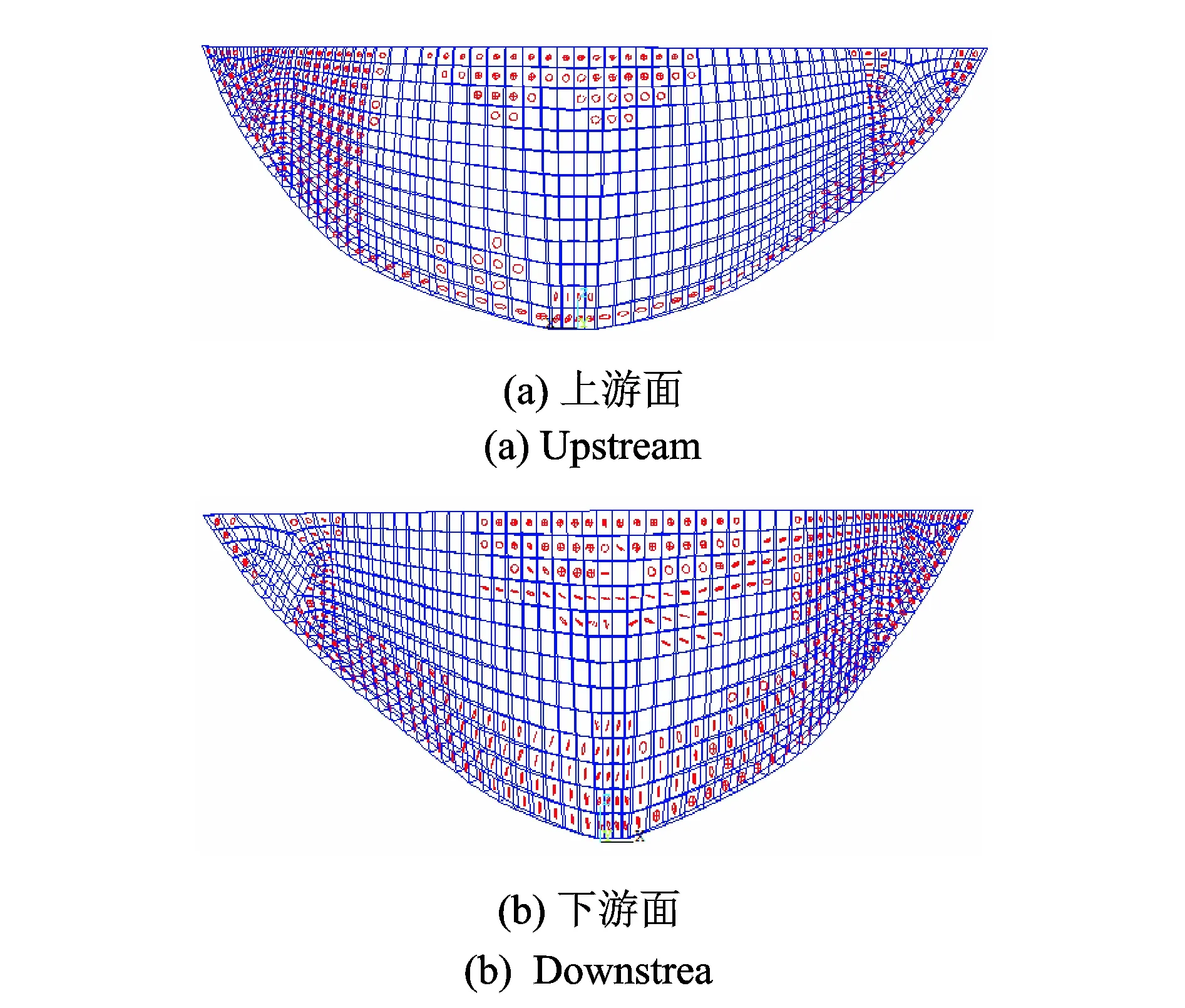
图5 持时延长后模型坝上、下游面损伤分布Fig.5 Damage distribution of model dam at extended duration

通过对比可以得到，0.5g地震动作用下，模型和原型结构在上游面周边及下游面损伤基本相同，但模型结构上游面拱冠梁附近出现的损伤在原型结构中没有出现。增大到0.6g后，原型上游面拱冠梁部位的损伤出现，与模型结构的损伤分布变得基本相同；但模型下游面坝趾部位又出现新的损伤，而原型还未出现，下游面又产生差别，直到继续增大加速度，原型相应部位出现的损伤与模型结构相同。增加地震动持时后，0.5g和0.6g地震动作用下结构上、下游面的损伤部位与未增加持时情况下得到的极限承载能力对应的加速度下的相同，但损伤程度更大。

从图6可见，模型和原型结构拱冠位移随着加速度的增大可分为3个阶段。第1阶段是结构位移反应出现拐点前(相当于非线性损伤开始出现)，原型和模型换算结果基本一致，表明满足弹性-重力相似可以保证弹性直至初始损伤的试验要求。第2阶段是位移反应加速发展之前(相当于结构出现损伤到损伤加速之间的阶段)的非线性损伤缓慢发展阶段，原型和模型换算结果之间是有差别的，表明弹脆性假定忽略材料的峰值后特征不满足断裂能相似，不能满足通过试验定量研究结构的损伤发展过程的要求。第3阶段是位移反应增长速率加大阶段(损伤加速发展，拐点可定义为极限抗震能力)，表明在结构损伤充分发展后，原型与模型的最终破坏模式和规律基本相同，据此确定结构极限抗震能力及所对应的极限加速度可以满足非线性破坏的试验要求。

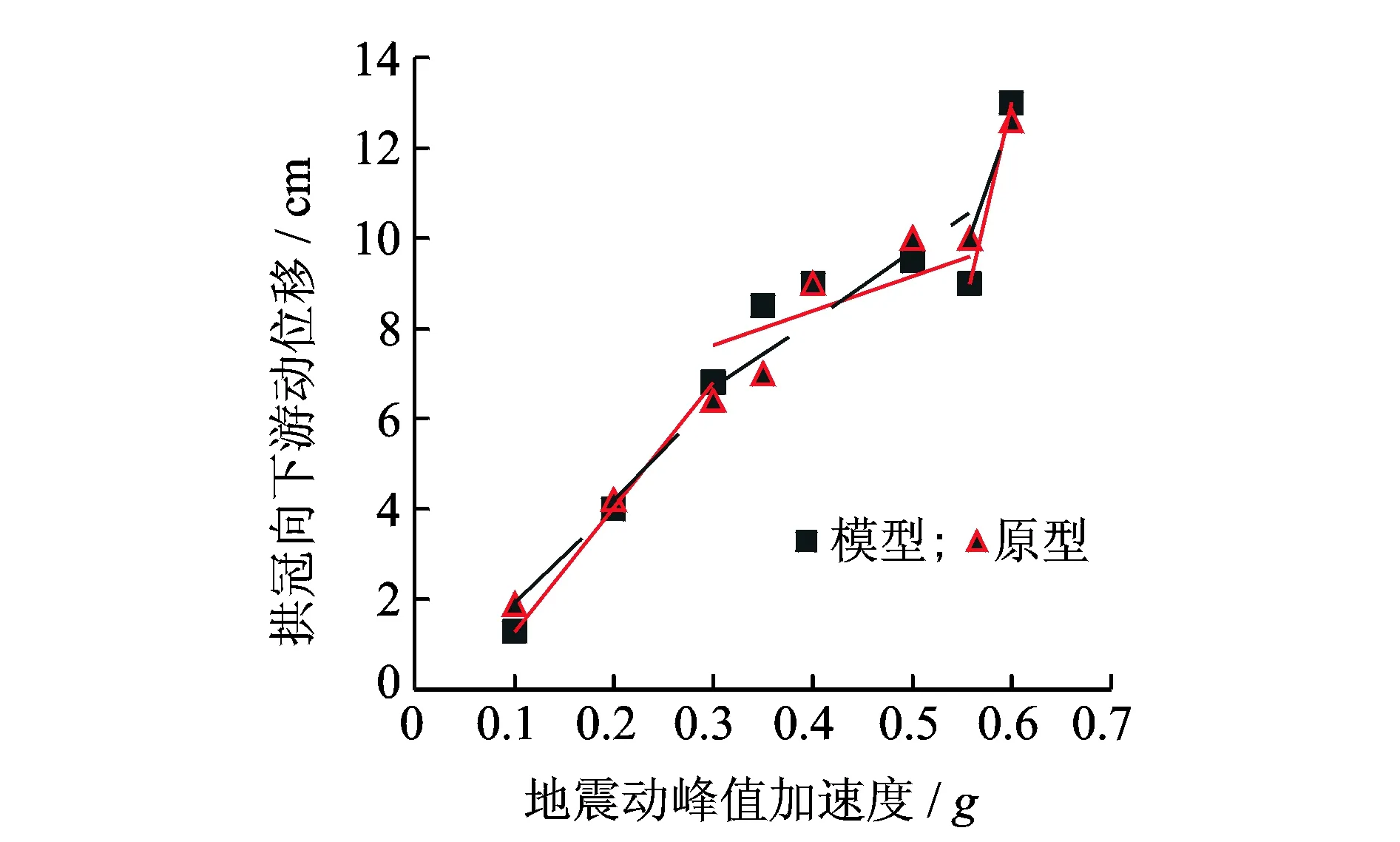
图6 模型与原型拱冠向下游动位移与地震动峰值加速度关系Fig.6 Comparison of maximum downstream displacement at arch crown of model and prototype dam

2 框架结构数值分析与论证

通过振动台试验，无论是确定结构的初始损伤加速度还是接近于临界破坏状态的极限抗震能力，弹性-重力相似率要求同时满足抗力和惯性力作用相似，材料的应力-应变曲线及地震动的持时特征都应该相似，但这种理想化的完全相似很难实现。根据计算结果分析可知：在结构出现初始损伤以前，无论是逐级加载还是地震动持时增加，对试验结果都没有影响；当地震动峰值加速度超过结构出现初始损伤的加速度以后，不同的加载方案对结构非线性的发展过程会产生影响，结构损伤部位和损伤程度在不同加载方案中发展过程也不同；但随着地震动峰值加速度的增大，趋近于极限承载能力时，损伤部位和损伤分布趋于一致。因此，逐级加载对于非线性损伤发展过程会有影响，但可以满足初始损伤加速度和极限抗震能力的试验要求。

下面以一个简单的五层框架结构为例来进一步阐述[12]。图7为单级和逐级加载下框架结构损伤分布和破坏区域的比较(逐级0.2g表示从0.05g开始以0.05g为增量直到0.2g，单级0.2g表示直接施加0.2g地震波，依此类推)。可以看出，随着地震动的增强，结构不同部位的损伤发展趋势是不同的。底层损伤虽然也在逐步增大，但是很缓慢，单级和逐级加载的损伤程度相同，没有形成破坏；而中部损伤发展加快，逐渐形成破坏区域。单级和逐级加载下结构损伤差别主要在失效区域内部，逐级和单级失效区域相同，相对位置不变，都可以反映出破坏模式。

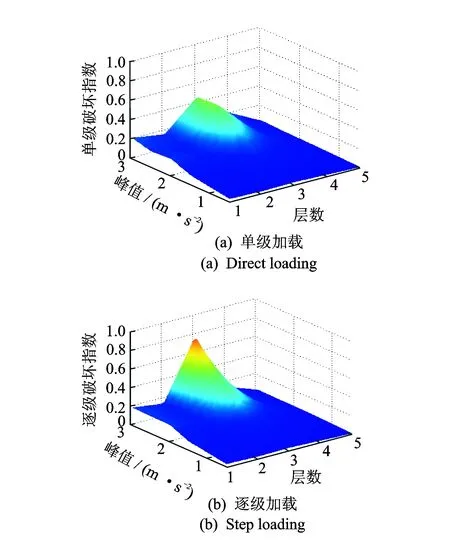
图7 损伤分布随地震动峰值加速度的变化Fig.7 Variation of damage distribution with of earthquake acceleration amplitude

图8为不同地震动持时和峰值加速度下的综合破坏指数变化规律的比较。可以看到，随着地震峰值加速度的增加，地震动持时的影响越来越大，但是到了30 s以后，增大速率趋于平缓。对此对应的是结构的最大位移和破坏指数，在0.25g结构出现损伤前，地震动持时基本没有影响。在0.30g出现损伤后，地震动持时开始有影响，地震动峰值较小时，地震动持时对结构破坏的影响较小，随着加速度增大，持时影响增加，但是持时增加到一定程度后，最大位移以及结构破坏指数都不再增加，而是基本保持不变，可以反映结构的极限抗震能力。

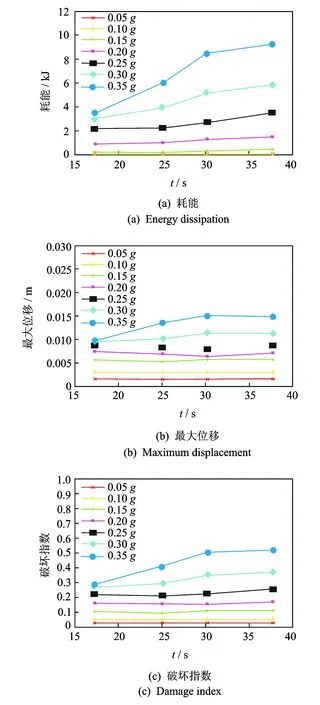
图8 结构响应随地震动有效持时和峰值的变化Fig.8 Variation of structural responses with earthquake duration

以上结果说明，只有在结构趋近于破坏的地震动作用下，地震动持时才有较大的影响。地震动逐级加载可能影响到结构的非线性发展过程，但是对于最终的破坏形式和极限抗震能力来讲，地震动峰值是更重要的因素。实际上，结构处于弹性阶段或损伤不大时，非线性变形所占比例很小，振动变形基本可恢复，因此地震动不大时满足弹性-重力相似关系的模型可以反映结构动力特性及临界损伤状态。随着地震动作用的增加，模型非线性逐渐增强，这一阶段由于逐级加载或材料峰值后特性差异使得损伤部位及其出现的先后次序有所差别。损伤路径的贯通或破坏形态与材料的模量和强度密切相关，但是当结构接近破坏阶段，损伤区域已经贯通而导致局部或整体破坏形态形成后，破坏区域边缘的强烈弱化或不连续特性使得材料模量及强度对临界失效或极限抗震能力的影响很小。对于确定性结构模型，最终的承载能力与失效路径发展过程无关，振动台破坏试验中的逐级加载模式及模型材料的峰值后特征影响不大。

3 结束语

基于弹脆性模量和强度的相似可以满足结构动力特性和初始损伤临界加速度的试验要求。满足残余强度相似的情况下，峰值后特性对失效模式及极限抗震能力的影响不大，可以采用极限抗震能力极限加速度的试验要求；但峰值后特性对于破坏路径及损伤失效的发展过程有较大影响，不能满足这一阶段的定量试验要求。在大体积混凝土的极限抗震能力的振动台模型试验中，保证模量和强度相似是研究结构初始损伤的关键因素。如果只是研究结构的破坏模式，则可以进一步降低材料的相似要求，可以只满足重力相似[9]。

在保持地震动频谱和加速度幅值特性相似的情况下，逐级加载到预定强度与增加地震动有效持时作用是等效的，对结构非线性损伤破坏的影响与材料峰值后特性的影响是类似的，都可以保证结构动力特性、损伤发生及破坏模式和极限抗震能力的试验要求，但损伤过程中能量输入及耗散的影响不能满足从损伤发生到失效破坏的中间发展过程的要求。

[1] 陈厚群,张艳红.评判混凝土高坝地震灾变的关键问题探讨[J].水利水电科技进展，2011，31(4):8-12.

Chen Houqun, Zhang Yanhong. Key problems for evaluating seismic catastrophe of high concrete dams[J]. Advances in Science and Technology of Water Resources, 2011,31(4):8-12. (in Chinese)

[2] 任亮，姜涛，李东升，等.微型FBG应变传感器在大坝模型试验中的应用[J].振动、测试与诊断，2013,33(2):277-284.

Ren Liang, Jiang Tao, Li Dongsheng, et al. Application of small FBG strain sensors in dam model experiment[J]. Journal of Vibration, Measurement & Diagnosis, 2013,33(2):277-284. (in Chinese)

[3] 王海波,李德玉,陈厚群.拱坝振动台动力破坏试验研究[J].土木工程学报,2006,39(7):110-119.

Wang Haibo, Li Deyu, Chen Houqun. Experimental study on the dynamic failure of arch dams using a shaking table[J]. China Civil Engineering Journal, 2006,39(7):110-119. (in Chinese)

[4] 周颖,于健,吕西林,等.高层钢框架-混凝土核心筒混合结构振动台试验研究[J].地震工程与工程振动,2012,32(2):98-106.

Zhou Ying, Yu Jian, Lü Xilin, et al. Shaking table model test of a high-rise hybrid structure building with steel frame-concrete core wall[J]. Earthquake Engineering and Engineering Vibration, 2012,32(2):98-106. (in Chinese)

[5] 王海波,李德玉,陈厚群.高拱坝极限抗震能力研究之挑战[C]∥现代水利水电工程抗震防灾研究与进展．西安：中国水力发电工程学会抗震防灾专业委员会，2013:17-23.

[6] Konagai K, Toyoaki N. Analog circuit to simulate dynamic soil-structure interaction in shaking table test[J]． Soil Dynamic and Earthquake Engineering, 1998,17:279-287.

[7] 王山山,徐敏.高拱坝动力特性与动力响应模型试验研究[J]. 实验力学,2012,27(4):414-420.

Wang Shanshan, Xu Min. Experimental study of dynamic characteristics and dynamic response model of high arch dam[J]. Journal of Experimental Mechanics, 2012,27(4):414-420. (in Chinese)

[8] Mir R A, Taylor C A. An experimental investigation into earthquake-induced failure of medium to low height concrete gravity dams[J]. Earthquake Engineering and Structural Dynamics, 1995,24(3):373-393.

[9] 林皋,朱彤,林蓓.结构动力模型试验的相似技巧[J].大连理工大学学报,2000,40(1): 1-8.

Lin Gao, Zhu Tong, Lin Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000,40(1):1-8. (in Chinese)

[10]张敏政．地震模拟试验中相似律应用的若干问题[J]．地震工程与工程振动，1997，17(2)：52-58．

Zhang Minzheng. Study on similitude laws for shaking table tests[J]. Earthquake Engineering and Engineering Vibration, 1997,17(2):52-58. (in Chinese)

[11]范书立,陈健云,王建涌,等.高拱坝振动台地震破坏试验研究及数值仿真[J].岩石力学与工程学报,2009,28(3):467-474.

Fan Shuli, Chen Jianyun, Wang Jianyong, et al. Experimental study and numerical simulation for seismic failure of high arch dam on shaking table[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(3):467-474. (in Chinese)

[12]陈光明.反应谱、地震动、结构易损性研究[D].大连：大连理工大学, 2011.

10.16450/j.cnki.issn.1004-6801.2016.01.010

*国家重点基础研究发展计划(“九七三”计划)资助项目(2013CB035905)；中央高校基本科研业务费专项资金资助项目(DUT14QY10)

2014-01-11；修回日期：2014-02-27

TV32+1； TV642.4； TH17

李静，女，1974年2月生，博士、副教授。主要研究方向为结构防灾减灾、重大工程风险管理方面的教学与研究。曾发表《高拱坝抗震性能评价的指标研究》(《水利学报》2014年第45卷第12期)等论文。 E-mail：lijing@dlut.edu.cn