分类话勾股

□于化平



分类话勾股

□于化平

在用勾股定理解题时，有时会遇到多种情况，稍不留神就会造成错解，这就需要我们利用分类讨论思想求解.为帮助同学们解决这类问题，现将勾股定理中需用到分类的问题加以浅析.

一、根据直角顶点位置分类

例1（2015·江西）如图1，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△PAB为直角三角形时，AP的长为______.

分析：利用分类讨论，当∠APB＝90°时，易知∠PAB为60°或30°，利用特殊三角形的性质求得AP的长；当∠ABP＝90°时，易得BP，利用勾股定理可得AP的长.

图1

图2

解：分三种情况讨论：

（1）如图2，当P在△ABC内部，∠APB＝90°时，

∵AO＝BO，

∴PO＝AO＝BO＝2.

又∠AOC＝60°，

∴△APO是等边三角形，

∴AP＝2.

（2）如图3，当P在△ABC外部，∠APB＝90°时，

∵AO＝BO，

∴PO＝AO＝BO＝2.

又∠AOC＝60°，

∴∠BAP＝30°.

∵AB＝4，∴BP＝2.

在Rt△ABP中，

图3

图4

（3）如图4，当∠ABP＝90°时，

∵BO＝AO＝2，

点评：本题涉及到的知识有勾股定理、含30°直角三角形的性质和直角三角形斜边的中线，而分类讨论、数形结合是解答此题的关键.

二、根据等腰三角形腰的位置不确定分类

例2（2015·通辽）如图5，在一张长为7cm、宽为5cm的矩形纸片上，剪下一个腰长为4cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为______.

图5

分析：因为等腰三角形腰的位置不明确，所以分三种情况进行讨论：

（1）如图5，△AEF为等腰直角三角形，直接利用面积公式求解即可；

（2）如图6，先利用勾股定理求出AE边上的高BF，再代入面积公式求解；

（3）如图7，先求出AE边上的高DF，再代入面积公式求解.

解：分三种情况计算：

（1）当AE＝AF＝4时，如图5，

图6

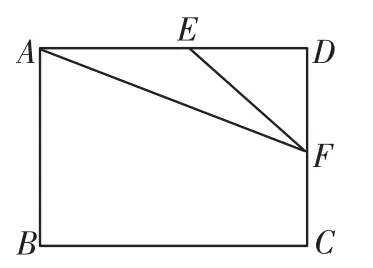
图7

（3）当AE＝EF＝4时，如图7，

则DE＝7-4＝3，

点评：本题主要考查矩形的角是直角的性质和勾股定理的运用，要根据三角形腰位置的不确定分情况讨论，有一定的难度.