多值区间直觉模糊软集

段梦雅,吴　涛,b,马　闯

(安徽大学 a.数学科学学院，b.教育部计算智能与信号处理重点实验室，合肥 230039)



多值区间直觉模糊软集

段梦雅a,吴涛a,b,马闯a

(安徽大学 a.数学科学学院，b.教育部计算智能与信号处理重点实验室，合肥 230039)

摘 要：软集理论作为一种处理不确定性问题的新数学工具，弥补了传统不确定性理论在参数不足的缺陷，近年来在理论上得到长足发展，但是忽略了元素的像为多值且隶属度和非隶属度为区间数情形的讨论。将多值直觉模糊软集推广到多值区间直觉模糊软集，并给出了多值区间直觉模糊软集的一些运算(交，并，补)，讨论了其相应的一些性质，从而能更好的描述和求解不确定问题。

关键词：模糊软集;多值直觉模糊集;多值区间直觉模糊软集

自1965年Zadeh提出了模糊集[1]的概念后，1986年Atanassovt提出直觉模糊集[2]的概念，和传统的模糊集相比较,直觉模糊集考虑了隶属度、非隶属度和犹豫度。而由于客观世界存在复杂性和不确定性，直觉模糊集中的隶属度和非隶属度难以用精准的数字来表示，于是Atanassov 提出了用区间数[3]来表示，同时提出区间模糊集的概念。然而随着科学的不断发展,人们发现，用传统的数学工具来描述和分析一些不确定性问题存在很多问题，直到1999年Molodtsov提出了软集理论[4]，这一重大研究成功弥补了传统模糊集理论在参数上的缺陷。现如今，软集理论作为一种新的数学工具被广泛运用到经济、工程和环境的问题中，和粗糙集理论、模糊集理论、区间数学作为数学工具来处理不确定性问题。文献[5]将软集理论与数据分析结合，文献[6]研究了软集理论与预测的联系，文献[7-9]将软集理论运用到决策中去。在那么多的软集理论研究当中，其中软集与模糊集的融合是一种重要的研究方向，文献[10]将模糊集与软集融合提出了模糊软集，文献[11]将直觉模糊集与软集融合提出了直觉模糊软集，文献[12]提出区间型直觉模糊软集。

基于对同一个评价对象不同的专家给出的结果不同，同一个专家从不同的角度来判断得到的结果也是不同的，张善文和S.Sebastian等人先后提出多值直觉模糊集的概念[13-14]。直到2014年江立辉等人将多值直觉模糊集与软集结合，提出了多值直觉模糊软集的概念[15]并研究了其相关性质。本文鉴于Atanassov、et al的思想，提出了多值区间直觉模糊集的概念，更能完善的描述客观问题，为解决实际问题提供了另一种方式，同时讨论了其相关的一些性质。

1基本概念

定义1(软集)[4]设U是一个非空有限集合，E是一个参数集，P(U)表示U的幂集，A⊆E。设F:A→P(U)为一个映射，则称(F,A)是U上的软集。

定义2(模糊软集)[10]设U是非空论域，E是一个参数集,I=[0,1],IU表示U上所有模糊集的全体，则称序数对(F,E)为论域U上的模糊软集(FSs),其中F:E→IU为参数集E到IU的映射，即对∀e∈E,F(e)={(u,μF(e)(x))|u∈U}∈IU其中，μF(e)(u)表示元素u属于模糊集F(e)的隶属度。

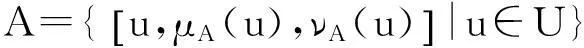
μA(u)⊂[0,1]νA(u)⊂[0,1],u∈U,

且满足:

supμA(u)+supνA(u)≤1,u∈U

显然，若infμA(u)=supμA(u)且infνA(u)=supνA(u)，则区间直觉模糊集退化为直觉模糊集。

定义5(多值直觉模糊软集)[15]设U是非空论域，E是非空集合，A⊆E。设F:A→MkIFS(U)，其中MkIFS(U)为k维多值直觉模糊软集，则称(F,A)为多值直觉模糊软集。记为：

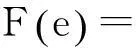
其中μij(ui)∈[0,1],i=1,2…s,j=1,2…k。

2多值区间直觉模糊软集

定义6设U是一个论域，E是一个参数集，设F:A→MkIVIFS(U))是一个的映射，其中MkIVIFS(U)表示U的K维多值区间直觉模糊集，A⊆E,则称(F,A)为U上的K维多值直觉模糊软集。

从定义上可以看出，多值区间直觉模糊软集是参数到MkIVIFS(U)上的映射。它是论域U上多值区间直觉模糊集的子集构成的参数族。对于∀e∈E,F(e)可以被看作是一组参数为e的多值区间直觉模糊软集(F,A)中的元素。

可记作：

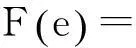
其中μij(ui)⊂[0,1],νij(ui)⊂[0,1] 且满足supμij(ui)+supνij(ui)≤1,ui∈U。

特别的，当k=1多值区间直觉模糊集退化为一般的区间直觉模糊软集。

例：假设U=(u1,u2,u3)是一组手机，A=(e1,e2,e3) 是一组参数，其中代表参数e1“价格”，包括贵的和便宜，e2代表参数“像素“，包括大和小，e3代表参数“电池损耗”，包括快和慢。可以定义下面的2维多值区间直觉模糊软集：

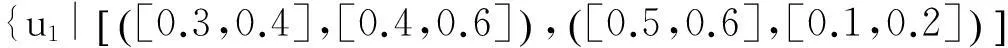
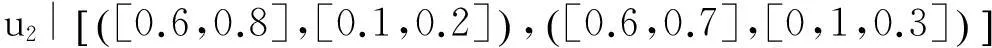
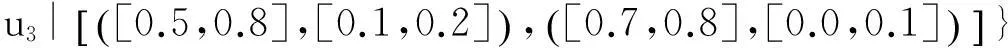
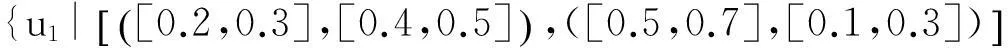
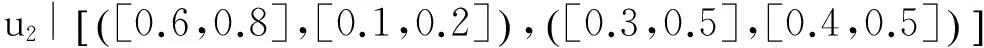
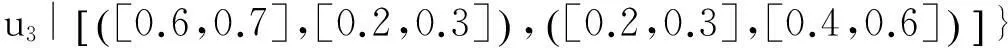
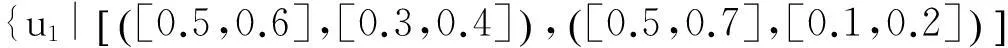
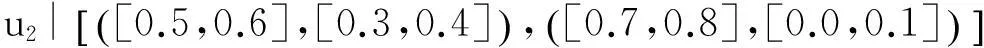
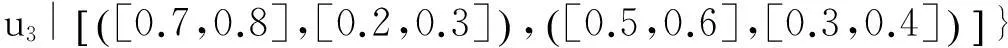
从上述软集(F,A)中可以看出手机属性的隶属度和非隶属度都是用区间数来表示的，用区间数来表示隶属度与非隶属度可以更贴合实际的表达物体的属性值，避免了找不到用精准数字表示造成的尴尬。另外还可以看出手机u1大的的隶属度为[0.3,0.4]，非隶属度为[0.4,0.6]；小的隶属度为[0.5,0.6]，非隶属度为[0.1,0.2]。

定义7设(F,A)是一个K维区间直觉模糊软集，F(e)表示参数e的K维区间直觉模糊值集，则在K维多值区间直觉模糊软集(F,A)中所有K维区间直觉模糊值集称为(F,A)的区间直觉模糊值族C(F,A),即C(F,A)={F(ε),ε∈A}。

定义8对于论域U上的两个K维区间直觉模糊软集(F,A)和(G,B)，称(F,A)是(G,B)的是K维区间直觉模糊软子集，记为(F,A)⊆(G,B)当满足条件：

(1)A⊆B

(2)∀e∈A,F(e)⊆G(e)即对∀ui∈U,有μijF(e)(ui)⊆μijG(e)(ui),νijF(e)(ui)⊇νijG(e)(ui), 则称(F,A)是(G,B)的子集。

定义9 设(F,A)和(G,B)是论域U上两个K维区间直觉模糊软集，如果(F,A)⊆(G,B),且(G,B)⊆(F,A),则称(F,A)和(G,B)相等，记为(F,A)≅(G,B)。

定义12定义两个K维区间直觉模糊软集(F,A),(G,B)的“交”运算为(F,A)∩(G,B)=(H,A×B)，其中H(δ,ε)=F(δ)∩G(ε)，∀(δ,ε)∈A×B,即：

μijH(δ,ε)(u)=μijF(δ)∩G(ε)(u)=[min{infμijF(δ)(u),infμijG(ε)},min{supμijF(δ)(u),supμijG(ε)}],

νijH(δ,ε)(u)=νijF(δ)∩G(ε)(u)=[max{infνijF(δ)(u),infνijG(ε)},max{supνijF(δ)(u),supνijG(ε)}]

定义13我们定义两个K维区间直觉模糊软集(F,A),(G,B)的“并”运算为：

((F,A)∪(G,B)=(O,A×B)，其中O(δ,ε)=F(δ)∨G(ε)，∀(δ,ε)∈A×B，

即：μijO(δ,ε)(u)=μijF(δ)∪G(ε)(u)=[max{infμijF(δ)(u),infμijG(ε)},max{supμijF(δ)(u),supμijG(ε)}],

νijO(δ,ε)(u)=νijF(δ)∪G(ε)(u)=[min{infνijF(δ)(u),infνijG(ε)},min{supνijF(δ)(u),supνijG(ε)}]

定义14K维区间直觉模糊软集(F,A) 的补集记为(F,A)C，且(F,A)C=(FC,A), 其中FC:A→MkIVIFS(U)是一个映射，满足：

FC(δ)={<ν(u),μ(u)>|u∈U,δ∈A}

显然(FC)C=F,((F,A)C)C=(F,A)。

定理(F,A),(G,B)和(E,C)论域U上的两个K维多值区间直觉模糊软集，则：

(1) (F,A)∪((G,B)∪(E,C))=((F,A)∪(G,B)∪(E,C));

(F,A)∩((G,B)∩(E,C))=((F,A)∩(G,B))∩(G,C) ;

(2) ((F,A)∪(G,B))C=(F,A)C∩(G,B)C;

((F,A)∩(G,B))C=(F,A)C∪(G,B)C;

(3) (F,A)⊇(G,A),(F,A)⊇(E,C)⟹(F,A)⊇(G,B)∪(E,C);

(F,A)⊆(G,B),(F,A)⊆(E,C)⟹(F,A)⊆(G,B)∩(E,C) ;

(4) (F,A)∩((G,B)∪(E,C))=((F,A)∩(G,B))∪((F,A)∩(E,C)) ;

(5) (F,A)∪((G,B)∩(E,C))=((F,A)∪(G,B))∩((F,A)∪(E,C));

(6) (F,A)⊆(G,B)⟹(G,B)C⊆(F,A)C;

(7) ((F,A)C)C=(F,A)

证明 现仅对(4)进行证明，(1)、(2)、(3)、(6)、(7)可以根据以上补集和交、并集的定义可证明得到，(5)的证明仿照(4)。

设

F(a)={<μijF(a)(ui),νijF(a)(ui)>},

G(b)={<μijG(b)(ui),νijG(b)(ui)>},

E(c)={<μijE(c)(ui),νijE(c)(ui)>}

则，

min{infμijF(a)(ui),max{infμijG(b)(ui),infμijE(c)(ui)}}=

max{min{infμijF(a)(ui),infμijG(b)(ui)},min{infμijF(a)(ui),infμijE(c)(ui)}};

同样的，

min{supμijF(a)(ui),max{supμijG(b)(ui),supμijE(c)(ui)}}=

max{min{supμijF(a)(ui),supμijG(b)(ui)},min{supμijF(a)(ui),supμijE(c)(ui)}};

又，

max{infνijF(a)(ui),min{infνijG(b)(ui),infνijE(c)(ui)}}=

min{max{infνijF(a)(ui),infνijG(b)(ui)},max{infνijF(a)(ui),infμijE(c)(ui)}};

同样的，

max{supνijF(a)(ui),min{supνijG(b)(ui),supνijE(c)(ui)}}=

min{max{supνijF(a)(ui),supνijG(b)(ui)},max{supνijF(a)(ui),supμijE(c)(ui)}};

所以，(F,A)∩((G,B)∪(E,C))=((F,A)∩(G,B))∪((F,A)∩(E,C))

3结束语

自软集的理论的提出，纷纷受到国内外学者的关注，尤其是与模糊理论的融合，使得在描述和解决问题上的能力得到很大提升。多值直觉模糊软集的提出让我们学会从不同角度来考虑问题，本文在此基础上考虑了隶属度和非隶属度为区间数的情况，从而提供了另一种解决不确定性问题的方法。

参考文献：

[1]William M，Lee M D.Hepatitis B Virus Infection[J].New England Journal of Medicine，1997，337(24)：1733-1745.

[2]Atanassov K．Intuitionistic Fuzzy Sets[J]．Fuzzy Sets and Systems,1986,20(1):87-96.

[3]ATANASSOV K,GARGOV G. Interval-valued Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems, 1989,31(3):343-349.

[4]Molodtsov D.Soft Set Theory-first Results[J].Computer and Mathematics with Applications，1999,37(4):9-31.

[5]Zou Y,Xiao Z.Data Analysis Approaches of Soft Sets under Incomplete Information[J].Knowledge-Based Syst, 2008, 21(8):941-945.

[6]Xiao Z，Gong K，Zou Y.A Combined Forecasting Approach Based on Fuzzy Soft Sets[J].Computers and Mathematics with Applications,2009,228(1):326-333.

[7]Das P K, Borgohain R.An Application of Fuzzy Soft Set in Multicriteria Decision Making Problem[J].International Journal of Computer Applications,2012,38(12):33-37.

[8]Maji P K,Biswas R,Roy A R.Soft Set Theory[J].Computers and Mathematics with Applications,2003,45(4):555-562.

[9]Maji P K,Biswas R,Roy A R.An Application of Soft sets in a Decision Making Problem[J].Computers and Mathematics with Applications,2002,44(8/9):1077-1038.

[10] Feng Feng,Young Bae Jun.An Adjustable Approach to Fuzzy Soft Set Based Decision Making [J].Journal of Computational and Applied Mathematics,2010,234:10-20.

[11] Jiang Y CH,Tang Y,Chen Q M.An Adjustable Approach to Intuitionsitic Fuzzy Soft Sets Based Decision Making [J].Applied Mathematical Modeling,2011,35:824-836.

[12] Jiang Y CH,Tang Y.Interval-valued Intuitionistic Fuzzy Soft Sets and Theirbproperties [J]. Computers and Mathematics with Applications,2010,60:906-918.

[13] Sebastian S,Ramakrishnan T V.Multi-fuzzy Sets:an Extension of Fuzzy Sets[J].Fuzzy Information，2011,11(1)：35-43.

[14] 张善文，李晓曼，雷英杰.多值直觉模糊集定义[J].计算机科学，2008,35(1):176-177.

[15] 江立辉，陈华友,丁芳洁，等,多值直觉模糊集[J].计算机工程与应用，2014,50(23):114-117.

[责任编辑：张永军]

Multi-valued Interval Intuitionistic Fuzzy Soft Set

DUAN Meng-yaa，WU Taoa，b，MA Chuanga

(a. School of Mathematical Sciences, b. Key Laboratory of Intelligent Computing & Signal Processing Ministry of Education, Anhui University, Hefei 230039, China)

Abstract:As a new mathematical tool to deal with uncertainty problems, soft set theory makes up for the shortages of the traditional uncertainty theory in parameters, and its theory and applications have get great progress. But the case that elements mapping are multiple value and the membership and non-membership are interval numbers has not been discussed. Multi-valued intuitionistic fuzzy soft set will be extended to multi-valued interval intuitionistic fuzzy soft set in this article, the operations of multi-valued interval intuitionistic fuzzy soft set and their properties are presented. Multi-valued interval intuitionistic fuzzy soft set can describe the practical uncertainty issue better.

Key words:fuzzy soft set; multi-valued intuitionistic fuzzy; multi-valued interval intuitionistic fuzzy soft set

中图分类号：O159

文献标识码：A

文章编号：1673-162X(2016)01-0009-04

作者简介：段梦雅(1990—)，女，安徽亳州人，安徽大学数学科学学院2013级硕士研究生，研究方向：智能计算和不确定理论；吴涛(1970—)，男，安徽阜阳人，安徽大学数学科学学院教授，博士，研究方向：智能计算和不确定理论。

基金项目：安徽省高等学校省级自然科学研究重点项目(KJ2013A033)、安徽大学研究生学术创新研究项目资助。

收稿日期：2015-06-20修回日期：2015-12-11