数学课堂教学与发散思维能力培养
杨彩苹
(建平县职业教育中心,辽宁 朝阳 122400)
数学课堂教学与发散思维能力培养
杨彩苹
(建平县职业教育中心,辽宁 朝阳 122400)
类比联想是研究数学问题的重要方法之一;既可以让学生主动地参与教学过程,又可以为学生的思维发展创造条件。同时要努力培养学生发现问题和提出问题的能力。
联想;类比;发散思维
学生探究发散能力的强弱是能否学好数学的一个很重要的因素,然而这种能力的提高,关键在于教师的引导和训练,根据本人的教学实践经验,运用联想与类比,进行探究式的教学,培养学生的发散思维能力。我在给学生讲“求证正四面体内任意一点P到四个面的距离之和为定值”这一练习题时,既不给学生直接讲如何证,也不任其他们自己考虑如何证。而是抓住“定值”二字,进行以下几个环节训练。
第一环节——联想,追亿旧知,填基石。我引导学生回想平面几何中的类似定值问题,学生在回忆中提出了:“求证正△ABC内任一点P到各边的距离之和为定值”这一问题后,继而帮助他们一起理清其证题思路:
首先,化零:连结PA、PB、PC得到△PAB、△PBC、△PCA;第二,架桥:利用S△ABC=S△PAB+S△PBC+S△PCA过渡获取结论。即通过分割将大三角形分成三个小三角形的面积之和,且揭示这一定值就是正△ABC的高。第二环节——类比,借思路找方法。师问:上述联想对我们所要解决的问题有何启示?并暗示:三角形能分割,立体是否也能分割。一经点拨,有几个学生争着回答:“可把三棱锥内的点P与各顶点相连,得到四个以点P为公共顶点的小棱锥。”第三环节——肯定鼓励完善步骤。学生的回答,我马上予以肯定,鼓励常识他们,并进一步考虑四个小锥体与大锥体的体积关系,寻找通往结论的桥梁,完善证题过程。
如图(1)不妨按一般情形,设S△ABC=S1,S△ABD=S2,S△ACD=S3,S△BCD=S4,以点A为顶点的锥体的高为h,点P到面ABC,面ABD,面ACD、面BCD的距离分别为d1、d2、d3、d4,
∵四面体ABCD为正四面体
∴S1=S2=S3=S4=S,则
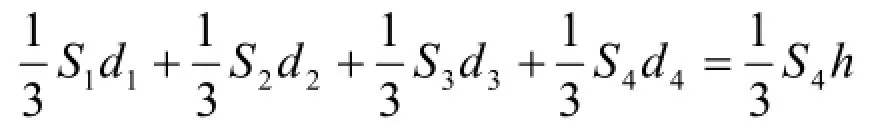
即S(d1+d2+d3+d4)=Sh
∴d1+d2+d3+d4=h,h为定值,即为锥体的高。
第四环节——概括思路,总结方法。待学生证题后,再诱导他们疏理思路过程:由“定值”(目标)产生联想(三角形分割)类比尝试(立体分割),最终通过等面积(探究)等体积,过渡实现目标。第五环节——借兴奋点,重燃火花。学生在具有深厚情趣的积极思维状态中完成了解题,学得轻松愉快,充满欢乐,显示出自豪的神态,陶醉在胜利的喜悦中,我进一步借助学生的兴奋点,重燃思维火花,引导进行如下探究发散思维训练。
(1)点P的位置变化
①点P在正四面体的某一个侧面上,如图(2)设P点在侧面ABC上时d1=0,则有d2+d3+d4=h②点P在正四体的某一条棱上,如图(3)设P点在棱AB上时d1=d2=0,则d3+d4=h③点P在正四面体的体外,如图(4)设点P在面BCD的下方,且在三面角A的内部,由
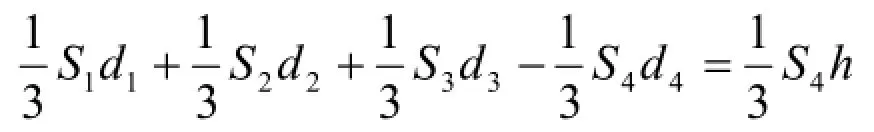
∴d1+d2+d3-d4=h

(2)正四面体的体形变化:①将正四体改为正三棱锥,不妨设A为顶点,⊿BCD为底面,此时,S1=S2=S3=S且是定值,则当P在体内时,
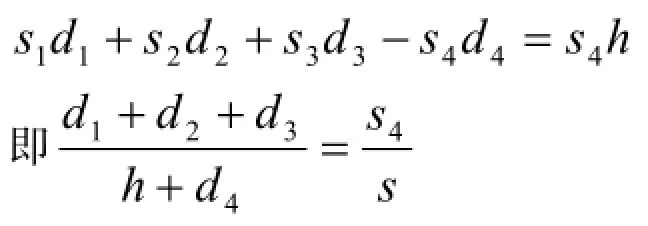
②将正四面体改为任意三棱锥
到此似乎大功告成了,但我穷追不舍,不错过一个一启即发的机会。我说:同学们,请你们回顾探究过程,从点P的位置变化到锥体的体形变化,即从‘形’的变化入手,进行了一系列的研究。但在研究过程中也涉及了一些量,并且其中的某些量始终没有考虑其特殊性,请你想想:①哪些量具有特殊性?②由这些量的特殊性你又能想到何种几何体?学生通过对研究过程中的量的比较,得出:P点到各面的距离可以相等;P点到各面所作垂线的垂足在一个球面上。我再次肯定了学生的发现,并给出了内切球和傍切球的概念与特性。同时给出了下列一个定理。“如果四面体的内切球半径为r,傍切球半径分别为r1、r2、 r3、r4,则
略证:不妨设r1、r2、r3、r4分别是三面角A、B、C、D内的傍切球的半径,四面体A-BCD体积为V,表面积为S,则由上述探究过程可得:

这样又使一道有一定难度的题成为思有路,解应手的容易题。通过联想、类此,由平面到空间,从体内到体外,从特殊几何体到一般几何体,利用分割与造形,自始至终,都贯穿等积这条知识线,使学生的思维得到了很好的强化,提高了能力,激发了学生的求知欲。
[1]盖虹,范东昕.反例教学法在高等数学教学中的应用[J]. 现代交际. 2015(12):145.
[2]石英.中高校数学教学中学生能力的培养[J]. 数理化学习.2015(10):12.
Mathematics classroom teaching and divergent thinking ability
YANG Cai-ping
(Jianping County Vocational Education Center, Chaoyang Liaoning 122400)
Analogy is Leno research one of the important methods of mathematics problems; Can let the students actively participate in the teaching process, and can create conditions for students' thinking development. At the same time try to train the students' ability to find problems and questions.
Association; Analogy; Divergent thinking
B848.2
A
10.3969/j.issn.1672-7304.2016.05.172
1672–7304(2016)05–0347–02
(责任编辑:吴 芳)
杨彩苹(1965-),女,辽宁朝阳人,研究方向:数学。

