岩溶地区注浆扩散半径理论计算研究

文/江永华 浙江省送变电工程公司 浙江杭州 310000

岩溶地区注浆扩散半径理论计算研究

文/江永华 浙江省送变电工程公司 浙江杭州 310000

本文基于波依塞维尔斯平面流体理论，并结合原杭州220kV变电站站址地质概况及采用的注浆方法，得出该工程岩溶注浆扩散半径的计算公式，分析表明：通过计算公式得出的扩散半径值与试注浆后现场取样结果较相近，说明该计算公式合理且适用于该工程场地注浆扩散半径的计算；注浆扩散半径R的平方与注浆压力成正比，与水泥浆液粘度成反比；当水灰比不变时，R值的增大速率随注浆压力的增大而减少；当注浆压力不变时， R值的减小速率随水泥浆液粘度的增大而减小；结合地质岩溶发育情况，可以从中寻找最适合该工程或类似地层条件的注浆压力及水泥浆液水灰比，使其注浆效果更经济、合理、准确。

岩溶；注浆扩散半径；注浆压力

本文基于波依塞维尔斯平面流体理论[1-2]，推导出在溶岩地区注浆扩散半径的计算公式，结合本工程的地质概况和试注浆情况，得出该工程场地注浆扩散半径的计算公式，并通过与试注浆扩散半径对比和分析该地区岩溶注浆扩散半径与注浆压力和水泥浆的水灰比（浆液粘度）的关系，认证了该计算公式适合本工程场地注浆扩散半径的计算，为此类地层条件下注浆施工的经济性和准确性提供了决策依据。

1、岩溶注浆扩散半径计算公式推导

由能量守衡定律可知，当注浆压力P保持不变时，注浆段断面浆液的平均流速和径向流距成反比，随着流距的增大，浆液的流速就越小，压力坡度也随之减小 [5]。

根据波依塞维尔斯的平面流体理论，注浆液在裂隙中的流速为

由流速为流量与过流断面积商可知

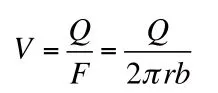
因此

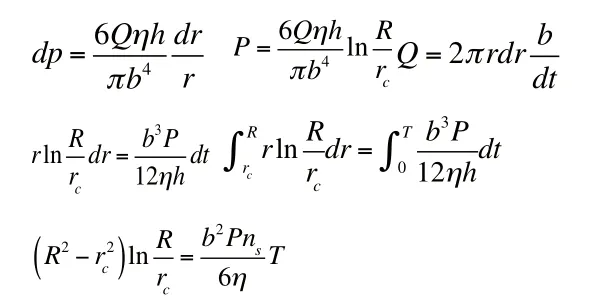
式中，R为注浆扩散半径（m）， 为注浆孔半径 ，b为裂隙宽度（m），P为注浆压力（MPa），为浆液粘度（Pa.s），T为注浆时间（s）， 为岩体裂隙率， 为注浆段的有效长度（m）。

2、工程计算实例概况

2.1 水文地质条件

站址范围内地下水类型主要以第四系空隙潜水为主，水位埋深0.5～1.5m。站址浅部地基土以上更新统冲洪积成因的粉质粘土、角砾（碎石）为主，下伏基岩为寒武系泥灰岩和石英岩。

2.2 溶洞发育情况

根据地质报告，本工程站址位于灰岩区，潜在的不良地质作用为岩溶塌陷。结合勘探点平面布置图综合分析，场地岩溶发育地段主要集中在场地中部，南北两端发育较少，深度一般不大。本次钻孔揭露全填充溶洞顶板基岩厚度0.4～2.1m，当填充物承载力无法承受上覆压力，顶板岩石塌落入溶洞，将挤溢洞中充填物到塌落空隙。

3、计算实例分析

3.1 计算过程

由于本工程注浆孔半径较小，可令 ，其中 很小，可忽略不计代入上式可得

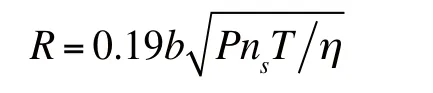
根据本站的地质勘察报告可知，岩体的裂隙率为25%～35%，取平均裂隙率28%；岩体中节理裂隙宽度为3～20mm，其中3～10mm的裂隙占大多数，取平均裂隙宽度6mm。

3.2 计算及结果分析

为分析岩溶注浆的扩散半径与注浆压力和水灰比（浆液粘度）的关系，本文分别取水灰比为0.5、0.6、0.75、1.0、1.2和注浆压力为0.8MPa、1.2 MPa、1.5 MPa、1.8 MPa、2.0 MPa代入式（12）进行分析，其中取注浆时间为30min，浆液粘度为40s时的粘度。结果如下图1、图2。

图1 扩散半径与注浆压力曲线图

图1中为当水灰比为0.5、0.6、0.75、1.0、1.2时扩散半径R与注浆压力P的关系曲线图，由图中可看出，当水灰比一定时，注浆扩散半径R的平方与注浆压力成正比，扩散半径随着注浆压力的增大而增大，但其增大速率随注浆压力的增大而减少。

图2 扩散半径与浆液粘度曲线图

图2中为当注浆压力P为0.8MPa、1.2 MPa、1.5 MPa、1.8 MPa、2.0 MPa时扩散半径R与水泥浆液粘度的关系曲线图，由图中可看出，一方面，当注浆压力P一定时，注浆扩散半径R的平方与水泥浆液粘度成反比，扩散半径随着水泥浆液粘度的增大而减小，但其减小速率随水泥浆液粘度的增大而减小。

本站试注浆材料采用32.5级普通硅酸盐水泥，水灰比为0.6，当注浆压力达到2.0MPa后上拔注浆管0.5m并继续注浆，结束后钻孔取样进行土工试验。钻孔取样发现离试注浆孔3m处有水泥痕迹，而在4m处无水泥痕迹，由此可知本站注浆扩散半径为3m～4m；按本文推导公式计算为R=2.998m（注浆压力为2.0MPa，浆液水灰比为0.6），与实际较相似，因此本文推导公式可以用来计算本站址岩溶注浆扩散半径。

结论：

1）本文推导出的计算公式充分考虑了注浆压力、水泥浆液粘度、岩溶地质情况、注浆时间等因素，通过计算公式得出的扩散半径值与试注浆后现场取样结果较相近，说明该计算公式合理且适用于该工程场地注浆扩散半径的计算。

2）结合本工程地质概况，本文分别考虑了不同注浆压力及水灰比对注浆扩散半径的影响，分析可知注浆扩散半径R的平方与注浆压力成正比，与水泥浆液粘度成反比；当水灰比不变时，R值的增大速率随注浆压力的增大而减少；当注浆压力不变时， R值的减小速率随水泥浆液粘度的增大而减小。

3）通过分析该注浆扩散半径计算公式，可以从中寻找最适合该工程或类似地层条件下的注浆压力及水泥浆液水灰比，使其注浆结果更经济、合理、准确。

[1]岩土注浆理论与工程实例协作组岩土注浆理论与工程实例[M].北京科学出版社,2001.

[2]阮文军.注浆扩散与浆液若干基本性能研究[J].岩土工程学报,2005,27(1):69～73.