抵御任意故障的H2动态输出反馈可靠控制研究
彭娜 姚波 王福忠


摘要:针对线性系统,基于线性矩阵不等式(LMI),给出具有抵御任意故障的H2动态输出反馈控制器的设计方案,所得到的结论不仅是能抵御执行器或传感器任何一类部件发生故障的完整性设计方案,而且能使系统达到给定的H2性能指标。使用比离散故障模型更具有实际意义的连续故障模型.一个数值例子说明所提方法的有效性。
关键词:任意故障动态输出;线性系统;线性矩阵不等式(LMI)
中图分类号:O231.1文献标识码:A
1引言
可靠控制是指针对系统部件可能发生的故障考虑在控制器设计过程中,所得到的可靠控制器可使闭环系统无论部件是否出现故障都能保持渐近稳定性和一定的性能指标。到目前为止,人们对于可靠控制的研究已经取得了很大的进展,文献[1,2]利用离散故障模型分别给出了考虑执行器故障和传感器故障的可靠控制器设计。文献[3]使用连续故障模型,给出了更实用的可靠控制器的设计方法。文献[4]基于LMI方法给出了抵御传感器故障的动态输出H2可靠控制器的设计。文献[5]研究了具有执行器故障的时变系统H2/H∞可靠控制器设计问题。然而,这样的可靠控制器并不能真正的保证系统的可靠。对于抵御传感器故障的可靠控制器,传感器没有发生故障而执行器发生了故障,可使系统失去稳定性;另一方面,抵御执行器故障的可靠控制系统发生了传感器故障,系统也将失去稳定性。迄今为止,人们对于抵御任意故障的可靠控制器的研究还不是十分广泛,文献[6]给出了考虑传感器或执行器任何一类部件发生故障的完整性设计方案。
本文使用连续故障模型,基于LMI给出了抵御任意故障的动态输出反馈H2可靠控制器存在的充分条件,并给出了其设计方法。
2问题描述
考虑如下线性系统:
(t)=Ax(t)+B1ω(t)+B2u(t)z(t)=C1x(t)+D1u(t)y(t)=C2x(t).(1)
其中x(t)∈Rn为系统状态变量,y(t)∈Rm是系统测量输出,u(t)∈Rm为控制输入,ω(t)∈Rl为平方可积的系统外部有界扰动输入,z(t)∈Rr是系统被控输出,A,B1,B2,C1,C2,D1为适当维数的常值矩阵。
对于系统(1),给出动态输出反馈控制器
·(t)=AK(t)+BKy(t)u(t)=CK(t).(2)
传感器故障模型描述如下
yf(t)=Fsy(t).(3)
故障处理:
Fs=diag(fs1,fs2,…,fsm),si≤fsi≤si0≤si≤1,si≥1,si≠si,(i=1,2,…,m)jsi=si-sisi+si,fsi0=12(si+si),lsi=fsi-fsi0fsi0
对于传感器故障矩阵可以得到如下关系:
Fs=Fs0(I+Ls),Ls≤Js≤I
执行器故障模型描述如下
uf(t)=Fau(t).(4)
故障处理:
Fa=diag(fa1,fa2,…,fap),ai≤fai≤ai0≤ai≤1,ai≥1,ai≠ai,(i=1,2,…,p)jai=ai-aiai+ai,fai0=12(ai+ai),lai=fai-fai0fai0
对于执行器故障矩阵可以得到如下关系:
Fa=Fa0(I+La),|La|≤Ja≤I
由系统(1),控制器(2)和故障模型(3)(4)构成了闭环系统,描述如下
·(t)=Ac(t)+Bcω(t)z(t)=Cc(t).(5)
计算技术与自动化2016年3月
第35卷第1期彭娜等:抵御任意故障的H2动态输出反馈可靠控制研究
其中
(t)=x(t)(t),Ac=AB2CkBkFsC2Ak,Bc=B10,Cc=C1D1Ck.
引理1[4]:对于系统(5),标量γFs>0和传感器故障模型(3),如果存在矩阵,,以及正定矩阵X>0,Y>0,适当参数α>0,使得下列LMIs
1+AT3T40
T+AT2CT1W21(α)W22(α)
3C1-I00
4WT21(α)T0-I0
0WT22(α)T00-I<0
XI
IY>0
∑li=1(0…ei…0)(BT1YB1)(0…ei…0)T<(γFs)2
其中
1=AX+XAT+B2+(B2)T
2=ATY+YA+FsC2+(FsC2)T
3=C1X+D1
4=WT11(α)C2X
有可行解(,,,X,Y),则系统存在考虑传感器故障的可靠H2控制器(2),相应参数矩阵可由下式确定
AK=N-1(T-YAX-C2X-YB2)(MT)-1BK=N-1CK=(MT)-1
矩阵M,N,W11(α),W21(α),W22(α)由下式确定,正标量α为适当参数。
I-XY=MNT,(6)
αFs0JsFs0Fs0-IFs0-Iα-1Js=W11(α)0W21(α)W22(α)(7)3主要结论
定理1:对于系统(5),标量γFs>0,γFa>0和故障模型(3)(4),如果存在矩阵,,以及正定矩阵X,Y,适当参数α>0,β>0,使得下列LMIs
1+AT3T40
T+AT2CT1W21(α)W22(α)
3C1-I00endprint
4WT21(α)T0-I0
0WT22(α)T00-I<0
Ω1+AΩT3ΩT40
T+ATΩ2CT100
Ω3C1-ID1U21(β)D1U22(β)
Ω40UT21(β)DT1-I0
00UT22(β)DT10-I<0
XI
IY>0
∑li=1(0…ei…0)(BT1YB1)(0…ei…0)T<(γFs)2
Ω1=AX+XAT+B2Fa+(B2Fa)T
Ω2=YA+ATY+C2+(C2)T
Ω3=C1X+D1Fa
Ω4=UT11(β)
有可行解(,,,X,Y),则系统存在抵御任意传感器故障的可靠H2控制器(2),相应参数矩阵可由下式确定
AK=N-1(T-YAX-C2X-YB2)(MT)-1BK=N-1CK=(MT)-1
M,N,W11(α),W21(α),W22(α),U11(α),U21(α),U22(α)由(6)(7)及下式确定,正标量α,β为适当参数。
βFa0JaFa0Fa0-IFa0-Iβ-1Ja=U11(β)0U21(β)U22(β).
证明:对于系统(5),设
Mt1=Σ1ΣT2+A(C1X+D1FaCKMT)TΣ2+ATΣ3CT1C1X+D1FaCKMTC1-I=Σ1ΣT2+A(C1X+D1CKMT)TΣ2+ATΣ3CT1C1X+D1CKMTC1-I+00(D1(Fa-I)CKMT)T000D1(Fa-I)CKMT00
Σ1=AX+XAT+B2FaCKMT+(B2FaCKMT)TΣ2=YAX+NBKC2X+YB2CKMT+NAKMTΣ3=YA+ATY+NBKC2+(NBKC2)T
结合Fa=Fa0(I+La),设
Mt2=00(D1(Fa0-I)CKMT)T000D1(Fa0-I)CKMT00+
00(D1Fa0LaCKMT)T000D1Fa0LaCKMT00
Mt3=00(D1Fa0LaCKMT)T000D1Fa0LaCKMT00=
Θ1LaΘ2+(Θ1LaΘ2)T≤βΘ1JaΘT1+β-1ΘT2JaΘ2
Θ1=00(D1Fa0)TT,
Θ2=CKMT00
Mt2≤β-1(CKMT)TJaCKMT0(D1(Fa0-I)CKMT)T000D1(Fa0-I)CKMT0βD1Fa0Ja(D1Fa0)T=
(CKMT)T0000D1β-1JaFa0-IFa0-IβFa0JaFa0
(CKMT)T0000D1T
设CKMT=,NBK=,
(YAX+C2X+YB2+NAKMT)T=,
结合式(6),可得
Mt1≤Ω1+AΠT3T+ATΩ2CT1Π3C1-I+
(CKMT)T000D1U21(β)D1U22(β)
(CKMT)T000D1U21(β)D1U22(β)T
根据Schur补引理,可得Mt1<0,则系统(5)存在抵御执行器故障的可靠H2控制器
再根据引理1,系统(5)存在抵御传感器故障的可靠可得H2控制器,则系统(5)存在抵御任意故障的的可靠H2控制器(2),定理得证。
4数值仿真
考虑如下系统:
A=-1011-2112-1,B1=-110,B2=100112,C1=1101-10,C2=022102,D1=0111.当应用抵御传感器故障的控制器,而系统执行器发生了故障。考虑执行器故障范围
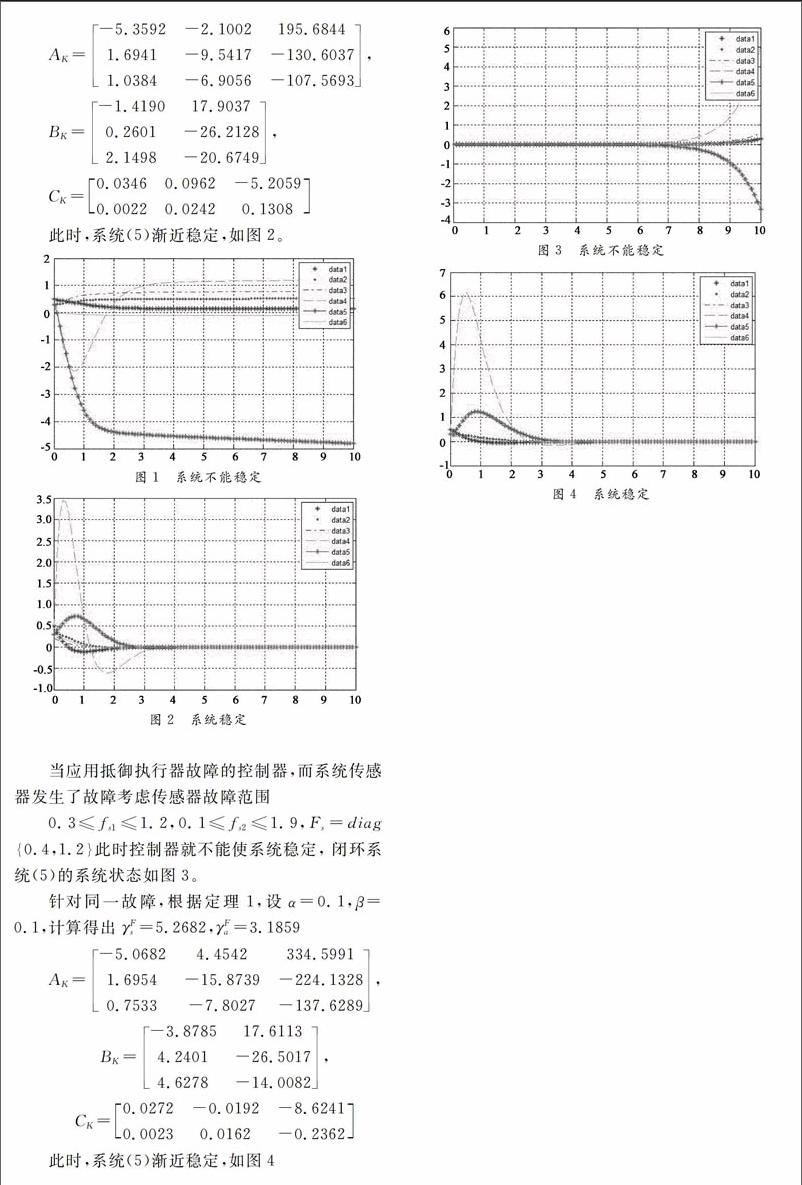
0.3≤fa1≤1.2,0.1≤fa2≤1.9,Fa=diag0.3,0.22,此时控制器就不能使系统稳定,闭环系统(5)的系统状态如图1。
针对同一故障,根据定理1,设α=0.1,β=0.1,计算得出γFs=5.9468,γFa=3.7729
AK=-5.3592-2.1002195.68441.6941-9.5417-130.60371.0384-6.9056-107.5693,
BK=-1.419017.90370.2601-26.21282.1498-20.6749,
CK=0.03460.0962-5.20590.00220.02420.1308
此时,系统(5)渐近稳定,如图2。
当应用抵御执行器故障的控制器,而系统传感器发生了故障考虑传感器故障范围
0.3≤fs1≤1.2,0.1≤fs2≤1.9,Fs=diag0.4,1.2此时控制器就不能使系统稳定,闭环系统(5)的系统状态如图3。
针对同一故障,根据定理1,设α=0.1,β=0.1,计算得出γFs=5.2682,γFa=3.1859
AK=-5.06824.4542334.59911.6954-15.8739-224.13280.7533-7.8027-137.6289,BK=-3.878517.61134.2401-26.50174.6278-14.0082,CK=0.0272-0.0192-8.62410.00230.0162-0.2362
此时,系统(5)渐近稳定,如图4
5结论
本文使用连续故障模型,基于LMI给出了抵御任意故障的动态输出反馈H2可靠控制器存在的充分条件,并给出了其设计方法,算例仿真证明了设计方法的有效性。endprint
参考文献
[1]VEILLETTERJ,MEDANICJV,PERKINSWR.Designofreliablecontrolsystem[J].IEEETransactiononAutomaticControl,1992,37(3):770-784.
[2]张春华,谭民.具有执行器完整性的容错控制器设计[J].控制理论与应用.2000,17(5):687-690.
[3]YANGGH,WANGJL,SOHYC.Reliabledesignforlinearsystem[J].Automatica,2001,37(5):717-725.
[4]NaPeng,FuzhongWang,BoYao.DesignofDynamicOutputFeedbackH2ReliableControlBasedonLMI[C]//ShihongQin,XiaolongLI.IndustrialEngineering,MachineDesignandAutomation&ComputerScienceandApplication.Sanya:WorldScientific,2014:479-483.
[5]WUYC,MALF,BOYM,LIUXH.ReliableMixedH2/H∞ControlforStochasticTimeVaryingSystemsAgainstActuatorFailures[J].Proceedingsofthe33rdChineseControlConference,1(2014)3059-3064.
[6]YAOB,ANZJ,WANGFZ,RobustandnonfragileHinfinityreliablecontrolforuncertainsystemswithellipsediskpoleconstraints[J].Proceedingofthe11thWorldCongressonIntelligentControlandAutomation,1(2014)3964-3696.
[7]HUH,JIANGB,YANGH.SHIP.NonfragileReliableH∞ControlforDeltaOperatorSwitchedSystems[J].Proceedingofthe11thWorldCongressonIntelligentControlandAutomation,1(2014)2180-2185.
[8]滕青芳,范多旺.不确定系统的鲁棒状态反馈区域极点配置[J].计算技术与自动化,2006,25(1),8-10.
[9]王福忠,姚波,张庆灵.基于LMI双故障动态输出反馈完整性控制[J].控制理论与应用,2006.976-980.
第35卷第1期2016年3月计算技术与自动化ComputingTechnologyandAutomationVol35,No1Mar.2016第35卷第1期2016年3月计算技术与自动化ComputingTechnologyandAutomationVol35,No1Mar.2016endprint

