精密测深中声速效应的影响及声速改正的计算

杜国元，黄金发，毕军芳

(1.长江水利委员会水文局长江口水文水资源勘测局，上海　200136；

2.上海祥阳水利勘测设计有限公司，上海　202150)



精密测深中声速效应的影响及声速改正的计算

杜国元1，黄金发2，毕军芳1

(1.长江水利委员会水文局长江口水文水资源勘测局，上海200136；

2.上海祥阳水利勘测设计有限公司，上海202150)

摘要：声速改正是水深测量中的一项重要内容。在存在声速梯度的条件下,正确的声速剖面测量和声速改正是影响测深精度的重要因素。以实例分析了某水库中水温垂向的分布及变化特点，同时计算了在不同条件下声速改正计算结果。

关键词：精密；测深；多波束；单波束；声速梯度；改正计算

1声速及声速测量

水体中的声速是一个比较活跃的物理变量，不同条件下声波传播的速度并不相同，与水体的温度、盐度和压力密切相关。而三个因素中，水温的变化对声速的影响最大。水温每增加1℃，声速约增加3.3 m/s。

很多情况下，特别是缺乏水体交换的深水条件下，水温变化的梯度可能很大，在静止的深水水库中，这个特点极为明显。在某些情况下，水底和水面的温度可能相差5℃以上，引起声速的梯度变化可超过15 m/s。

在深海条件下，由于受到日照、风和洋流等因素的影响，不同层的物理特性(主要是温度)变化更为复杂。在垂直方向上大致可以划分出4个声速变化层：表面层、温跃层、渐变层、等温层，其声速剖面的变化基本表现为声速从近似恒定到负声速梯度，再到正声速梯度的变化趋势。最上层主要受到温度的影响，最下一层主要受到水压力的影响[1]。

在深水水库中，由于水的流动性差，水体交换缓慢，一般水库的盐度可忽略不计，其水体温度在垂直方向上的分布主要受季节性的影响。从水面到数百米深的水底，温度多呈现下降的趋势。在一定的深度以上，温度变化不大，一旦到达某一深度，温度开始急剧下降，超过某一深度以后，水温又趋于稳定，这种水温从稳定—降低—稳定的变化规律在深水水库中普遍存在。水温的垂直变化带来了声速剖面在垂向上的分布变化。

为了确定不同环境下声速测量的最优公式，很多文献上均对此进行了深入的研究[2] [3]。《水运工程测量规范》(JTS131-2012)和《海道测量规范》(GB12327-1998)也推荐了各自的公式用以计算不同条件下单层的水深声速。通过计算，按两规范所荐的公式计算出的声速差值约1 m/s。

声速计用于测量海水中声波传播速度，其基本原理是通过测量声波在海水中固定距离内的传播时间来计算声速。主要的工作原理有相位法和环鸣法等。在20世纪前期，采用间接测量法测定海水中的声速，即测量海水的温度、盐度及深度等参数，然后按经验公式计算海水中的声速。到20世纪40年代末才开始研制直接测量声速的仪器，1957年出现了环鸣式声速仪，60年代开始广泛使用声速仪测量海水声速。运用相位法原理的声速仪，因其测量范围比较小，未能广泛应用。现代声速仪多采用环鸣法(即脉冲循环法)原理。

环鸣式声速仪的探头由换能器及固定在一定距离的反射面组成，测量时置于水中。在电信号激励下，换能器发出起始声脉冲，声波经过水中长度固定的通道到达反射面，再反射回换能器。放大了的接收信号重新激励发射器，触发第二个声脉冲。如此循环，形成一系列脉冲。测出脉冲重复的频率,并对电路的时延进行补偿,则声速等于脉冲重复频率与声程长度的乘积。

由于水体中(特别是海区)的水温和盐度在垂直方向上存在梯度分布，引起声速在垂直方向上存在梯度分布，而且位置不同，声速梯度分布也不尽相同。从原理上说，由于声速梯度的存在，不同的测点需采用该测点测量时声速传播路径上的平均声速(可采用声速剖面仪测定)，实际上，不可能在测量水深的同时去测量每个测点声速传播路径上的平均声速，为此采用一个假设：在水域一定范围内，声速剖面的分布是相同的。实际操作时，测量一个最深位置的声速剖面来代替一定范围内的声速剖面。采用后处理的方法对每个测点进行声速改正。

2声速传播及声线追踪

声波在两种介质的界面上或者同一种介质性质发生变化时会发生反射和折射，且符合反射、折射定律，折射的程度与声速差有关，声线总是向着声速较小的区域弯曲。其反射和折射规律符合Snell法则，Snell法则可表述为：

(1)

式(1)中，θi和θi+1是声速为Ci和Ci+1相邻介质层界面处波束的入射角和折射角，P为Snell常数。入射角≠0时，波束在界面处发生折射，若经历的水柱中有N+1个不同的介质层，则产生N次折射，波束的实际传播路径为一个折线(图1所示)。Snell法则不但解释了波束在水中的折射特性，还给出了求解声线路径的算法。

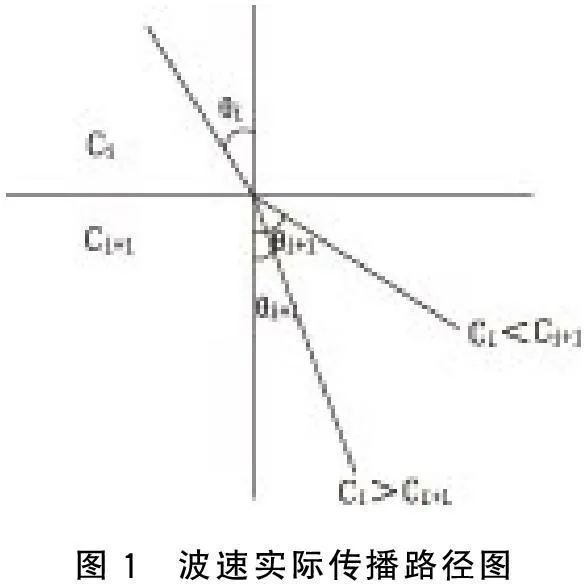
图1 波速实际传播路径图

在多波束测量中，由于存在大量入射角不为零的波束，波束在水体中的波束脚印(投射点)的位置需要进行精确计算，投射点相对于波束发射点的垂直距离也需重新进行计算。为达此目的，需要采用高精度的声线跟踪算法。

声线追踪是建立在声速剖面基础上的一种波束脚印相对于船体坐标系坐标计算的一种方法。声线追踪常采用层追加的方法，即将声速剖面内两个相邻的声速采样点划分为一个层，层内的声速变化可假设为零梯度或为常梯度。

严密的声线追踪计算过程复杂，特别是声速变化梯度变化复杂的条件下。为了简化计算，可以采用等效声速剖面法进行声线改正。等效声速剖面法声线改正中深度计算如下：

(2)

式(2)中，geq为等效的常声速剖面的梯度，Req为对应的等声线弧段曲率半径，其计算方法可查阅有关文献，在此不再赘述。

采用等效声速剖面法进行声线改正，深度计算仅利用了表层声速C0和参考深度Z0，实际声速剖面仅用于相对面积差的计算。

3精密单波束测深的声速改正

在精密单波束测量中，由于波束角较大，在一定船体姿态变化的幅度内，可以认为波束角的入射角为零，此时声线追踪的计算主要是对波束在垂直方向上的误差进行修正。

从原理上说，由于声速梯度的存在，在测量的时候，不同的测点需采用该测点测量时声速传播路径上的平均声速(可采用声速剖面仪测定)，实际上不可能在测量水深的同时去测量每个测点声速传播路径上的平均声速，为此采用了一个假设：在水域一定范围内，声速剖面的分布是相同的。实际操作时，测量一个最深位置的声速剖面来代替一定范围内的声速剖面。采用后处理的方法对每个测点进行声速改正，

理论上，平均声速Cm应为声波传播全路径上的瞬时声速平均值，若采用水深参数h表达应为：

(3)

式(3)中，D为从换能器到水底的深度。

由于不可能知道声速传播路径上每一处的声速，故在实际计算中采用式(3)进行抽样离散的计算：

(4)

式(4)中，n为声波路径上的抽样数，也就是分层数；di为各水层的厚度，Ci为各水层的声速值，n值越大，即抽样数越多，结果越准确。式(4)可称为计算平均声速的精确公式。

实际上在水深测量的时候，都将一个固定的设计声速C0(一般取1 500 m/s或者某一位置表层声速)输入测深仪，此时测得的每一个位置的水深实际上是一个近似水深，需要在后处理时进行声速改正。

(5)

从式(5)可知，测深值的声速改正值与观测深度成正比，水深越大，声速改正值越大，还与声速差成正比，改正值数值的大小见表1所示。

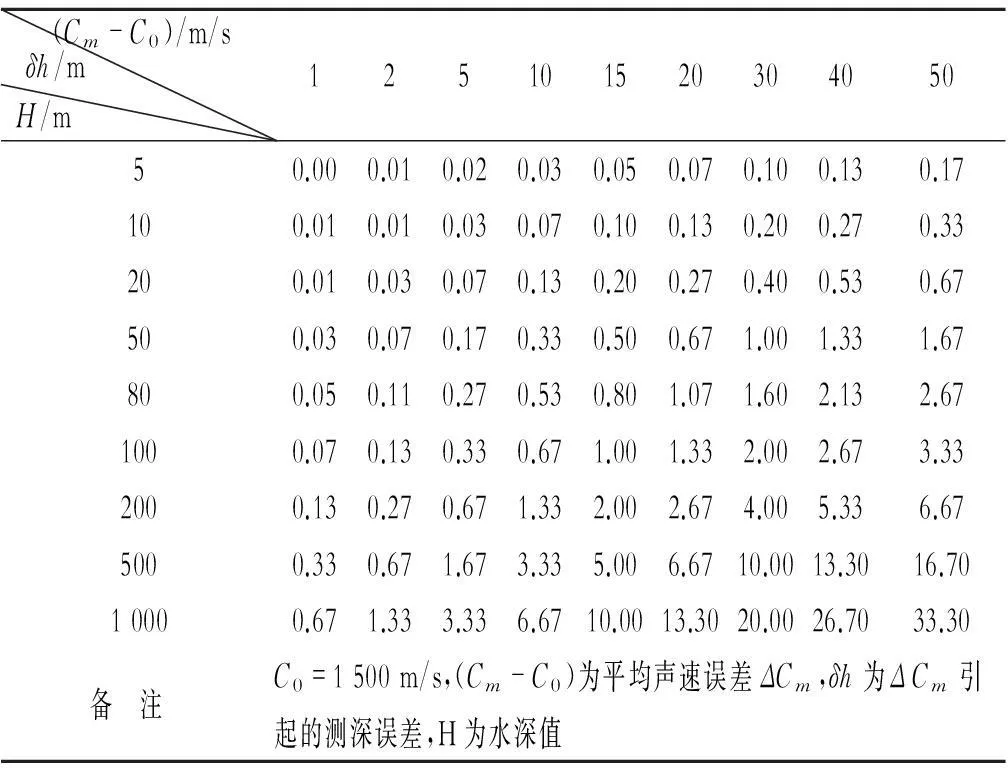
表1　改正值数值表

4某深水水库精密水深测量中的声速改正计算

某深水水库，最深处水深约160 m，根据历年来水库中温度剖面的监测结果，水库中存在温度梯度，且季节性变化十分明显。下图2为某年5月份在水库某固定位置测量得到的温度剖面。

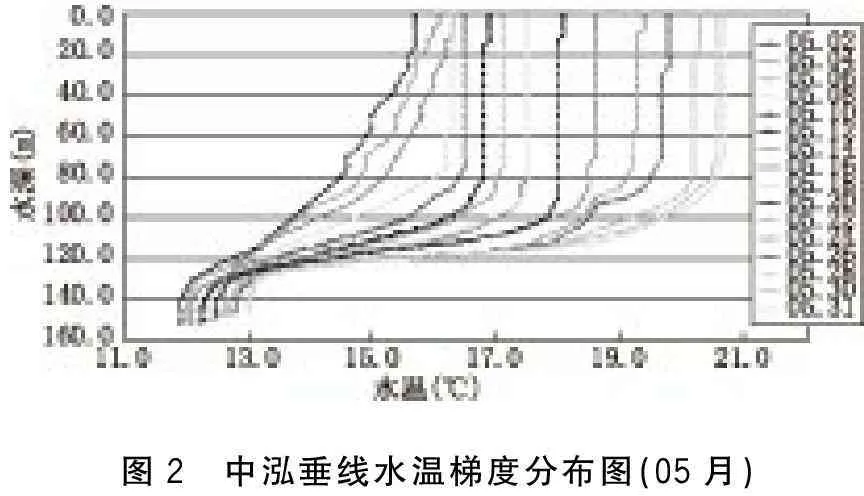
图2 中泓垂线水温梯度分布图(05月)

图3为水库相同位置6月8日的声速垂直分布剖面。

从图2可以看出，该水库的温度梯度分布在5月份的不同时间内一直在变化，且变化非常明显，从图3可以看出，在6月8日，上层水面与水底的声速变化达到了30 m/s。

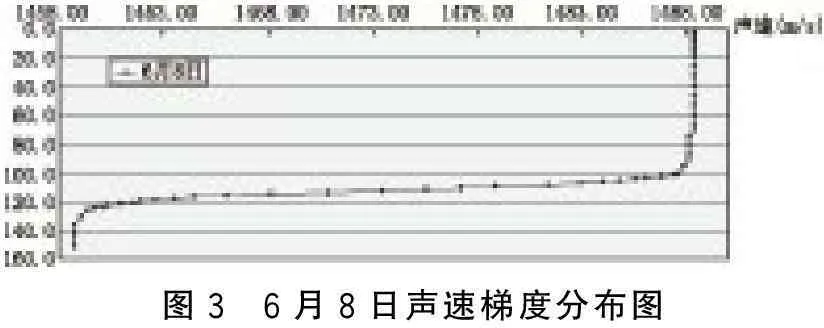
图3 6月8日声速梯度分布图

在实际的水深测量中，测深仪的声速输入(设计声速)可以采用三种：标准声速1 500 m/s、表层声速、平均声速(声速剖面测量位置)。无论采用哪种声速，由于各测点水深不同，故各测深点声线传播路径上的平均声速不同，测深仪测量得到的水深值只是实际水深的近似值，各测深值需要根据各自位置计算出来的平均声速进行声速改正。理论上说，采用的设计声速应该与测区内大部分地方的平均声速差异最小。

该水库的水深分布如图4所示。

假定测量时间为图3中的6月8日，在实际测量中采用的是表层声速1 488.3 m/s，则水深测量中各点的声速改正分布如图5所示。

假定在实际测量中采用的是声速剖面测量位置的平均声速1 480.6 m/s，则水深测量中各点的声速改正分布如图6所示。

假定在实际测量中采用的是声速剖面测量位置的标准声速1 500 m/s，则水深测量中各点的声速改正分布如图7所示。

5小结

通过以上分析和实例计算，可得出以下结论：

(1)对于多波束测深，需要采用声线追踪来计算波束脚印，同时需要对水深进行声速改正；对于单波束测深，一般只需要进行深度改正。深度改正的精度直接决定了测深精度。

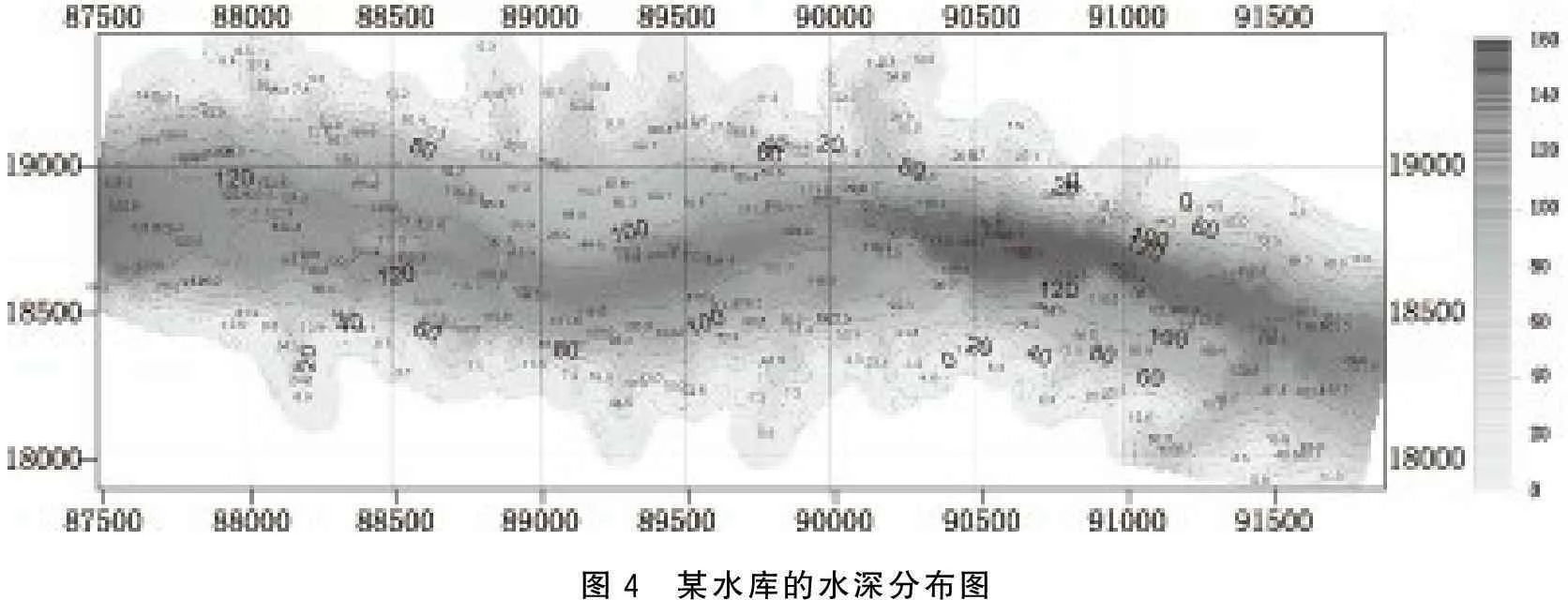
图4 某水库的水深分布图

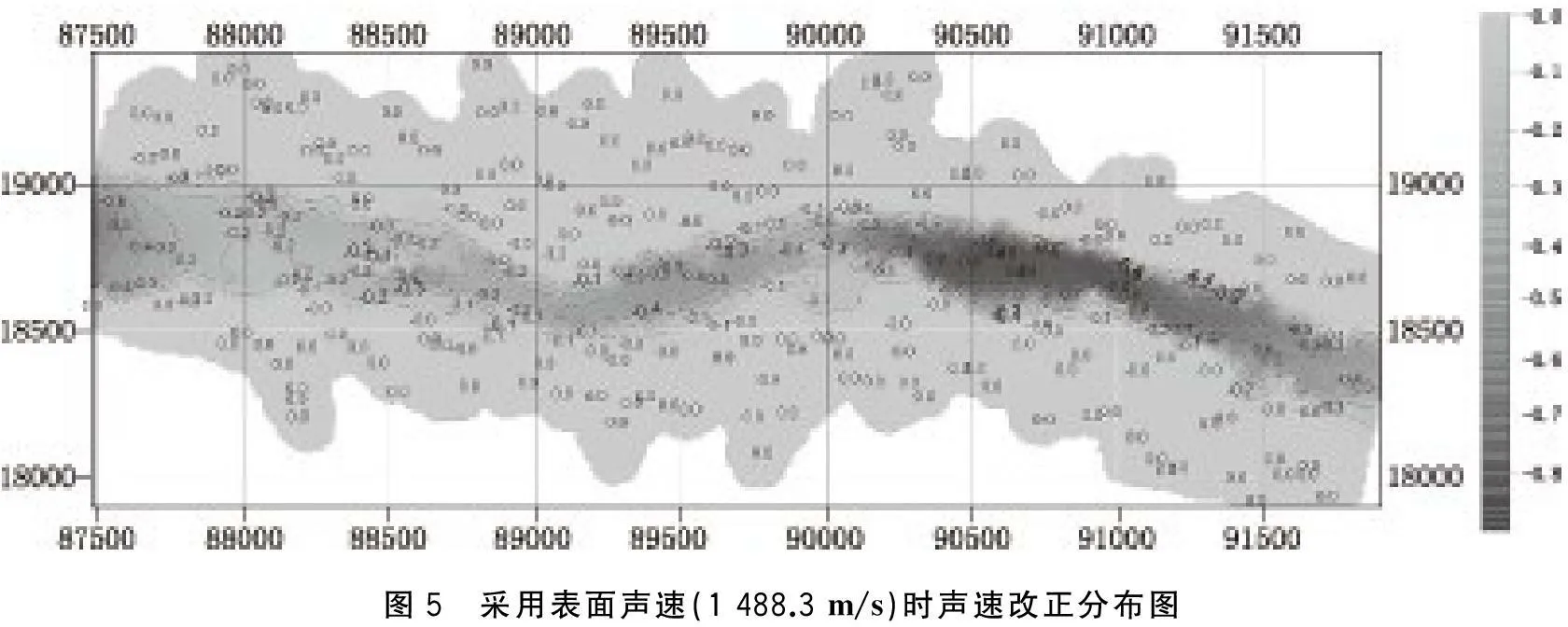
图5 采用表面声速(1488.3m/s)时声速改正分布图

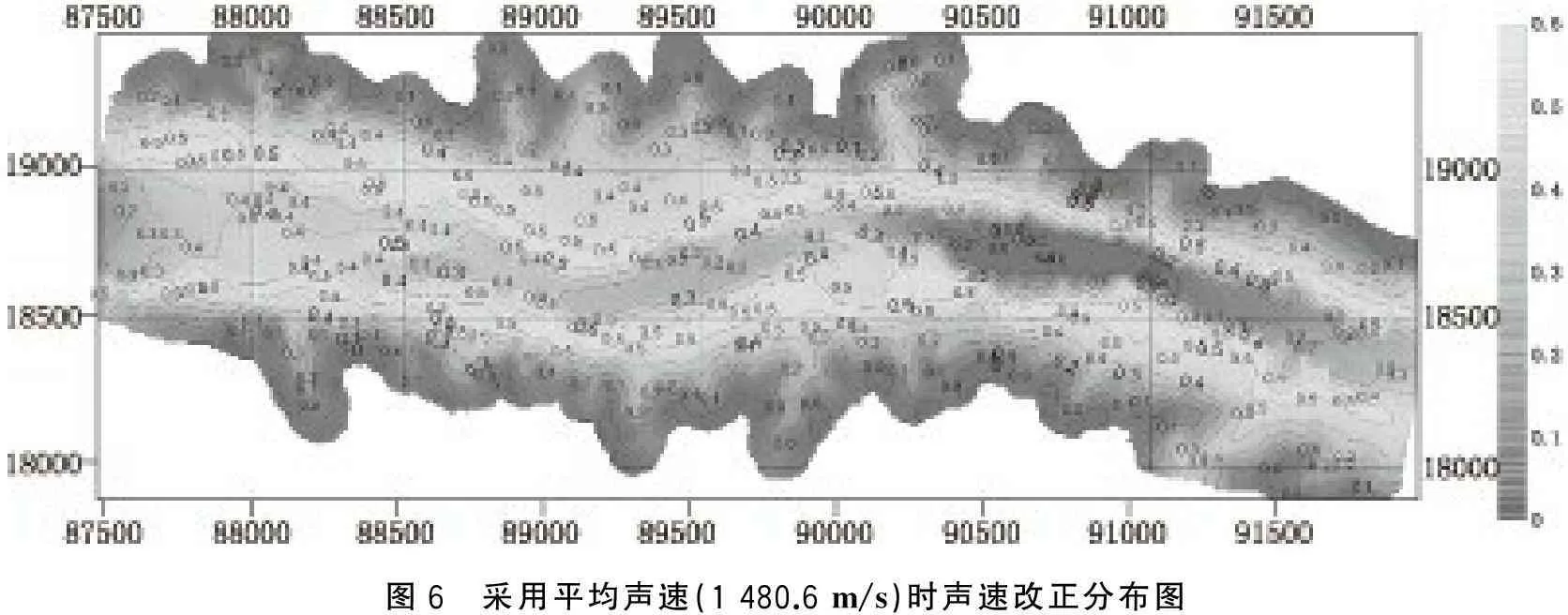
图6 采用平均声速(1480.6m/s)时声速改正分布图

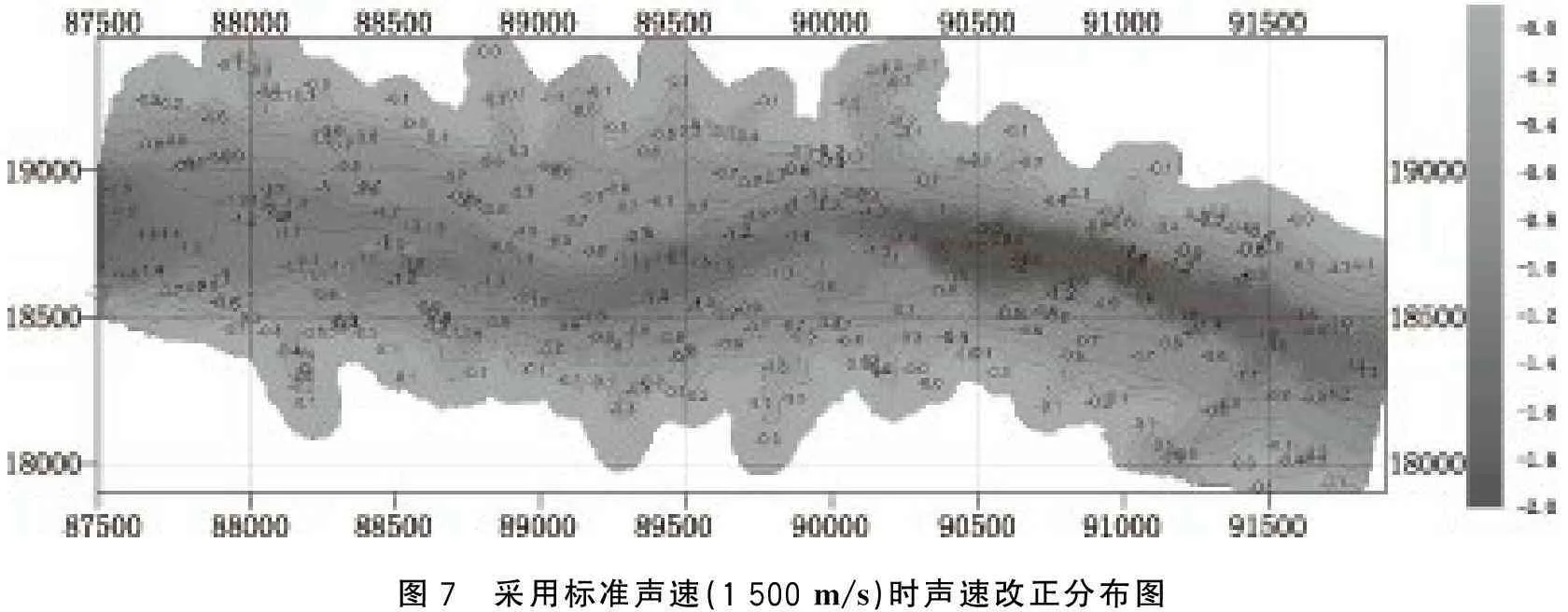
图7 采用标准声速(1500m/s)时声速改正分布图

(2)单波束的声速改正相对简单，但也是一项必要的工作，特别是在深水水库的测量中更应当引起足够的重视。

(3)无论是海水还是淡水中，声速梯度普遍存在，其季节性变化十分明显。在进行精密测深时，声速剖面的测量是重要的。在水深变化较大，缺少水体交换的条件下，必须测量声速剖面。

参考文献：

[1]张清华，刘铜仿.海水声速对多波束测深的影晌[J].台湾海峡，2001,(11).

[2]周丰年，赵建虎，周才扬. 多波束测深系统最优声速公式的确定[J].台湾海峡，2001,(4).

[3]管铮.西北太平洋大于200米水深回声测深改正公式[J].测绘学报，1987,(1).

[4]刘雁春.海洋测深空间结构及其数据处理[M].北京：测绘出版社，2003.

The Effect of Sound Velocity in Precise Bathymetric Survey and the Method to Calculate the Correction of Sounding Wave Velocity

DU Guo-yuan1, HUANG Jin-fa2，BI Jun-fang1

(1. Bureau of Surveying and Mapping of the Estuary of the Yangtze River, Shanghai 210036, China;

2. Shanghai Xiangyang Water Conservancy Survey &Design Co., Ltd. Shanghai 202150, China)

Abstract：The correction of sound wave velocity is very important in bathymetric survey. Under the condition of the existence of sound velocity gradient, correct sound velocity profile measurement and sound velocity correction are important factors affecting the accuracy of sounding. Based on the example, vertical distribution of water temperature in a reservoir and characteristics of its change are analyzed, and at the same time, correction calculation results of sound velocity under different conditions are calculated.

Key words：precise bathymetric survey; multi-beam; single-beam; sound velocity gradient; correction calculation

DOI:10.14079/j.cnki.cn42-1745/tv.2016.01.006

中图分类号：P229

文献标识码：B

文章编号：1673-0496(2016)01-0018-04

作者简介：杜国元(1964-)，男，湖北阳新人，工程师，大学，主要从事工程测量和海洋测绘工作。

收稿日期：2016-01-05