一类中立型泛函微分方程的测度伪概自守解

冯天维

（兰州交通大学数理学院，甘肃　兰州　730070）



一类中立型泛函微分方程的测度伪概自守解

冯天维

（兰州交通大学数理学院，甘肃兰州730070）

摘要：讨论了Banach空间中的一类抽象中立型泛函微分方程的测度伪概自守解。在利普希茨条件下，建立了μ测度伪概自守函数对时间变元γi（t）扰动不变性的一个充分性条件,并且对一些复合定理进行了推广和改进，同时，借助于测度伪概自守函数合适的组合定理结合算子半群理论和不动点定理,建立了此方程测度伪概自守解的存在性和唯一性。

关键词：测度伪概自守函数；抽象中立型泛函微分方程；不动点定理

DOI10.3969/j.issn.1672-6375.2016.01.022

0　引言

在20世纪中期，Bochner首次提出了概自守函数概念,它是概周期函数的一个自然推广[1]。其后,许多数学工作者对Banach空间上发展方程的概自守性质进行了广泛而深入研究。N'Guerekata提出了渐近概自守函数的概念[7]。Liang等人[9]介绍了关于伪概自守函数的概念。N'Guerekata和Pankov引入了Stepanov概自守函数的概念并详细论证了函数空间的完备性和组合定理[8]。Blot等人[2]给出了Banach空间中的加权伪概自守函数的定义。Chang等人[10]建立了Stepanov加权伪概自守函数的性质和新组合定理,并对带有加权伪概自守系数的一类非线性方程,研究了它们的加权伪概自守解的存在性。最近,Blot等人[3]应用测度理论定义了遍历函数,并且给出了测度伪概自守函数的概念和相关定理。Luo在文献[4,5]中分别讨论了一类中立型微分方程和一类半线性积分方程测度伪概自守解的存在性。

本论述主要在文献[6]的基础上，讨论了如下抽象中立型泛函偏微分方程测度伪概自守解的存在性和唯一性：

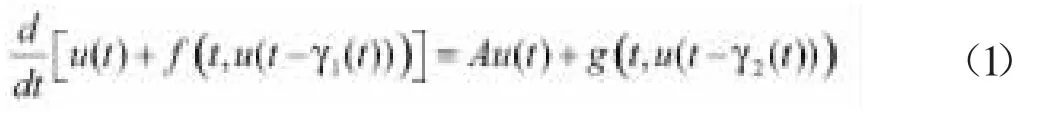
1　预备知识

定义1.1[3]设连续函数称为是概自守的,如果对任意的实数序列都存在一个子序列使得

对任意的t∈R是可以明确定义的,并且有

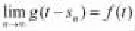
记这类函数构成的集合为AA（R，X）。

定义1.2[3]设B⊂X是任意一个有界集合,连续函数称为是概自守的,如果对于任意的t∈R有f（t，x）是概自守的,对所有x∈B是一致成立的,记这类函数组成的集合为AA（R×X，X）。

定义1.3[3]设μ∈M,有界连续函数称为μ-遍历,如果f满足下式

将这类函数空间记为ε（R，X，μ）。

注1.1[4]设μ∈M,则具有一致收敛拓扑性的空间ε（R，X，μ）和ε（R×X，X，μ）是Banach空间。

定义1.4[4]设μ∈M,连续函数称为是μ-伪概自守的,如果f可以分解为其中，将这类函数记为,因此，可得。

引理1.1[3]设μ∈M，τ∈R对于上的正测度μτ定义为

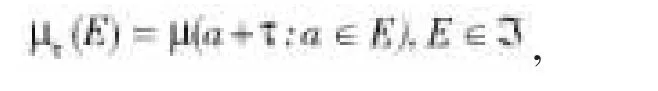
对μ∈M,本论述总是假定以下条件成立:

（H0）对任意τ∈R，存在α＞0和一个有界区间I使得

注1.2[3]设μ∈M且满足（H0）,则ε（R，X，μ）是平移不变的,同时PAA（R，X，μ）也具有平移不变性,且是Banach空间。

1.3[10]设μ∈M且满足（H0），f∈PAA（R，X，μ），则函数分解为是唯一的，其中。

下面给出本论述所需要的基本假设条件：

2　主要结果

定义2.1对于任意t∈R,连续函数u∈BC（R，X）称为中立型系统（1）适度解,若在（-∞，t）上是可积的且

定理2.1设μ∈R，γ1和γ2满足条件（H3）。若

证明令μ＝μ1＋μ2∈PAA（R，X，μ），其中μ1∈AA （X）,μ2∈ε（R，X，μ），由（H3）的假设,γi可逆且。另一方面对于r＞0,有

注意到条件（H3）中的假设

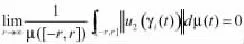
引理2.1[4]设μ∈M，f=g+h∈PAA（R×X，X，μ）若条件（Ⅰ）和（Ⅱ）成立：

（Ⅰ）对于任意的x∈X和t∈R，f（t，x）在有界子集Q⊂X上是一致连续的；

（Ⅱ）对于任意的x∈X和t∈R，g（t，x）在有界子集Q⊂X上是一致连续的。

定理2.2设μ∈M,μ∈PAA（R，X，μ）,假设条件（H1）成立,若函数ν满足,那么对于任意的t∈R,有ν∈PAA（R，X，μ）。

证明因μ∈PAA（R，X，μ）有μ＝μ1＋μ2∈PAA（R，X，μ）,且μ1∈AA（R，X），μ2∈ε（R，X，μ）,使得

上式由μ2∈ε（R，X，μ）和勒贝格控制收敛定理亦可得。

定理2.3设μ∈M，μ∈PAA（R，X，μ）,若函数ω满足，那么对于任意的t∈R,有 ω∈PAA（R，X，μ）。

定理2.4设μ∈M，条件（H1）-（H3）成立。若

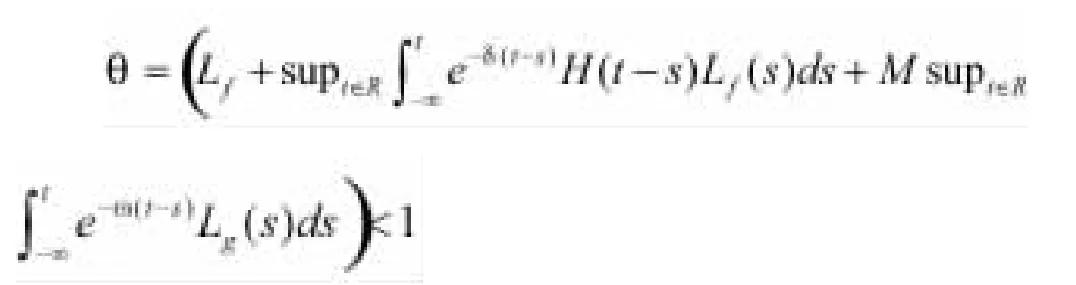
那么方程（1）有唯一的μ测度伪概自守适度解。

证明设Γ：PAA（R，X，μ）→PAA（R，X，μ）是非线性算子满足

又

进而从定理2.2和定理2.3可得

其次证明Γ有唯一的不动点。

由θ＜0知Γ在PAA（R，X，μ）有唯一不动点,即方程（1）有μ测度伪概自守适度解。

参考文献：

［1］S.Bochner.Continuous mappings of almost automorphic and almost periodic functions,Proc.Natl.Acad.Sci.USA，52 （1964）：907-910.

［2］J.Blot,G.M.Mophou,G.M.N’Guerekata,D.Pennequin. Weighted pseudo almost automorphic functions and applications to abstract dierential equations［J］.Nonlinear Anal，71 （2009）：903-909.

［3］J.Blot,P.Cleutat,K.Ezzinbi.Measure theory and pseudo almost automorphic functions:New developments and aplications［J］.Nonlinear Anal，75（2012）：2426-2447.

［4］Yong-Kui Chang,Xiao-Xia Luo.Existence of μ-pseudo almost automorphic solutions to a neutral dierential equation by interpolation theory［J］.Filomat，28（3）（2014）：603-614.

［5］Yong-Kui Chang,Xiao-Xia Luo,G.M.N’Guerekata. Asymptotically typed solutions to a semilinear integral equation［J］.Integral Equations Appl，26（3）（2014）：323-343.

［6］T.Diagana,E.M.Hernandez.Existence and uniqueness of pseudo almost periodic solutions to some abstract partial neutral functional-dierential equations and applications［J］. Math.Anal.Appl.327（2007）：776-791.

［7］G.M.N’Guerekata.Sue les solutions presqu’automorphes dequations dierentielles abstraites［J］,annales des scinence Mathematqiues du Qu ebec,51（1981）：69-79.

［8］G.M.N’Guerekata,A.Pankov.Stepanov-like almost automorphic functions and monotone evolution equations,Nonlinear Anal，68（2008）：2658-2667.

［9］J.Liang,J.Zhang,T.J.Xiao.Composition of pseudo almost automorphic and asymptotically almost automorphic functions ［J］.Math.Anal.Appl.340（2008）：1493-1499.

［10］R.Zhang,Y.K.Chang,G.M.N’Guerekata.Weighted pseudo almost automorphic mild solutions to semi-linear integral equations with Sp-weighted pseudo almost automorphic coecients［J］.Discrete contin.Dyn.Syst-A 33 （2013）：5525-5537.

作者简介：冯天维（1989-），男,甘肃武威人,研究生在读,主要研究方向：中立型泛函微分方程的测度伪概自守解。

收稿日期：2015-12-10

中图分类号：O175

文献标识码：A