保形映射的一个充分必要条件

祝颖润，曹俊飞，王瑞庭

(1.吉林大学珠海学院公共基础课教学与研究中心，广东 珠海 519041；

2.广东第二师范学院数学系，广东 广州 510310)



·研究快报·

保形映射的一个充分必要条件

祝颖润1，曹俊飞2，王瑞庭1

(1.吉林大学珠海学院公共基础课教学与研究中心，广东 珠海 519041；

2.广东第二师范学院数学系，广东 广州 510310)

[摘要]通过对保形映射和范数的研究，得到并证明了保形映射的一个充分必要条件.

[关键词]分形；保形映射；范数

1预备知识

保形映射是一种保持所有交线之间的夹角不变的数学变换.保形映射是复分析和分形几何的基本概念，在物理等领域中有重要的应用.[1-2]因此，判断一个映射是否为保形映射是十分重要且有意义的.文献[1]对Rd中的cookie-cutter集的性质进行了深入研究，在关键条件“对于任意的x∈X，‖DS(x)‖‖DS(x)-1‖=1”下，获得了cookie-cutter集Hausdorff维数压力函数的Bowen公式；证明了支持在cookie-cutter集上的自相似测度，自保形测度及gibbs测度的存在性，并且分析了这些测度的维数谱；证明了cookie-cutter集的Hausdorff维数的二阶密度的存在性.

作者对文献[1]的关键条件“对于任意的x∈X，‖DS(x)‖‖DS(x)-1‖=1”进行深入研究后，发现此条件是保形映射的一个充分必要条件.

定义1[1，3-4]设X⊂Rd是一个凸的闭集且满足X=cl(intX).如果映射S：X→X满足

‖S(x)-S(y)‖=λ‖x-y‖，∀x，y∈X，

S(x)=λRx+b，∀x∈X，

其中λ为相似比，是一个常数，R是一个正交变换，b为Rd的一个向量.则称该映射S是一个自相似映射.

定义2[1，3-4]设X⊂Rd是一个凸闭区域，X=cl(intX).如果映射S：X→X满足

‖DSx(z1)-DSx(z2)‖=λ(x)‖z1-z2‖，∀x∈X，

其中DS(x)表示S在点x处的向量导数，简记为DSx(DS(x)是S在点x处的雅可比矩阵)，z1，z2是Rd中的两个向量.亦即

S(x)=λ(x)Rx，∀x∈X，

其中λ(x)是x的一个正函数，R是一个正交变换.则称此映射S是一个保形变换.

定义3[5]对于一个向量xn×1，x的欧式范数定义为

定义4[5]矩阵范数定义如下：

2主要结果

定理1如果X⊂Rd是一个凸闭集，X=cl(intX)，则映射S：X→X是保形映射的充分必要条件是对任意x∈X，‖DS(x)‖‖DS(x)-1‖=1.

证明必要性.如果S：X→X是一个保形变换，则对于任意的x∈X，向量导数DS(x)是一个相似矩阵.[5]因此，DS(x)=λ(x)R(x)，其中λ(x)是一个正值函数，并且R(x)是一个依赖于x的正交变换.通过直接计算可得：

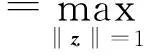
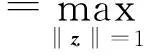
从而

‖DS(x)‖‖DS(x)-1‖=1，∀x∈X.

充分性.如果‖DS(x)‖‖DS(x)-1‖=1，∀x∈X，则存在一个常数λ(x)>0，对于任意的z∈{t：‖t‖=1}，‖DSx(z)‖=λ(x).

假设z1，z2∈{t：‖t‖=1}，使得‖DSx(z1)‖=λ1(x)‖z1‖，‖DSx(z2)‖=λ2(x)‖z2‖，其中λ1(x)≠λ2(x).不失一般性，不妨设λ1(x)>λ2(x).若DSx(z2)=z3，则z2=(DSx)-1(z3).通过计算可得：

因此

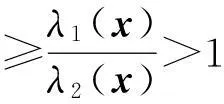
上式与已知条件矛盾，故假设不成立.

综上，对任意的z1，z2∈X，‖DSx(z1)-DSx(z2)‖=‖DSx(z1-z2)‖=λ(x)‖z1-z2‖，即S：X→X是一个保形变换.

[参考文献]

[1]LIANG J R，YU Z G，REN F Y.Messures and their dimension spectrums for cookie-cutter sets in Rd[J].Acta Math Appli Sinica，2000，16：9-21.

[2]丁丹，郭晶，盛中平.有关Hausdorff测度的两类覆盖形式[J].东北师大学报(自然科学版)，2013，45(4)：1-5.

[3]FALCONER K J.Fractal geometry mathematical foundations and applications[M].New York：John Wiley & Sons，1990：149-179.

[4]FALCONER K J.Techniques in fractal geometry[M].New York：John Wiley & Sons，1997：41-80.

[5]MEYER C D.Matrix analysis and applied linear algebra[M].Philadelphia：SIAM，2001：270-280.

[6]MATTILA P.Geometry of sets and measure in Euclidean spaces，fractals and rectifiability[M].Cambridge：Cambridge Univ Press，1995：51-52.

(责任编辑：李亚军)

A necessary and sufficient condition on conformal mapping

ZHU Ying-run1，CAO Jun-fei2，WANG Rui-ting1

(1.Education and Research Center of Basic Courses，Zhuhai College of Jilin University，Zhuhai 519041，China；2.Department of Mathematics，Guangdong University of Education，Guangzhou 510310，China)

Abstract:Through the study of preserved conformal mapping and norm，this paper concluded and proved a necessary and sufficient condition of conformal mapping.

Keywords:fractal；conformal mapping；norm

[中图分类号]O 174.12[学科代码]110·41

[文献标志码]A

[作者简介]祝颖润(1984—)，男，讲师，主要从事分形几何与拓扑动力系统研究；通讯作者：曹俊飞(1982—)，男，博士，副教授，主要从事随机微分动力系统研究.

[基金项目]国家自然科学基金资助项目(11301090)；广东第二师范学院博士与教授研究基金资助项目(2013ARF02).

[收稿日期]2015-09-11

[文章编号]1000-1832(2016)01-0159-02

[DOI]10.16163/j.cnki.22-1123/n.2016.01.031