一种基于Kalman滤波的雷达数据抗野值方法
张亚松,任宏光
(中国空空导弹研究院,河南 洛阳 471009)
一种基于Kalman滤波的雷达数据抗野值方法
张亚松,任宏光
(中国空空导弹研究院,河南 洛阳471009)
摘要:在对雷达测量数据的实际滤波过程中,带有野值的测量数据值将导致滤波系统产生记忆效应和误差,甚至导致滤波过程发散,严重影响处理结果的精度;从滤波算法的原理和工程实践的实际出发,以测量值与一步预测值的残差即“新息”为基础,提出了一种新的野值判别和剔除的简单易行算法;通过仿真对比计算,可以更为有效地消除野值对滤波的不良影响,提高测量精度。
关键词:Kalman滤波;野值剔除
Citation format:ZHANG Ya-song, REN Hong-guang.One Method of Radar Data Restraining Outliers on Kalman Filter [J].Journal of Ordnance Equipment Engineering,2016(2):45-47.
在雷达量测数据预处理过程中,目标跟踪系统观测的坐标值,不仅包含随机误差,有时由于传感器本身或者人工实施干扰或者数据传输的种种原因,都有可能使测量值含有远大于随机误差的粗大误差,通常称为野值。其特点是幅值大、持续时间短、无规律。如果不将这些野值预先剔除,将给数据处理带来很大的误差,并且带有野值的测量值将导致滤波系统产生记忆效应和误差,导致滤波发散、计算溢出。因此,在对目标坐标实施滤波之前,要对测量值进行合理性检验。合理的测量值予以保留,不合理测量值的判为野值并予以剔除。本文提出一种基于Kalman滤波的野值有效辨识与剔除算法。
1雷达目标跟踪Kalman滤波器
雷达目标的跟踪系统中,一般按照恒速直线运动的轨迹运动,运动目标的转弯、机动等引起的加速度可以看作是恒速直线运动的摄动。
在直角坐标系中,目标运动的数学模型为
(1)
(2)
(3)
(4)
目标运动规律在离散化状态方程的基础上可模拟为

(5)


(6)

2修正Kalman滤波算法
卡尔曼滤波是利用基于状态方程的递推方式进行估计的,它给出的总是状态变量的估计值。Kalman滤波所要估计的量,是一个具有随机误差的离散线性系统的状态向量。
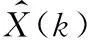
状态估计的一步预测方程:
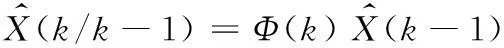
(7)
一步预测均方误差:
(8)
状态更新方程:

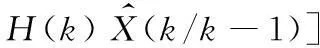
(9)
其中,滤波增益阵K(k)=P(k/k-1)HΤ(k)[H(k)P(k/k-1)HΤ(k)+R(k)]-1
估计均方误差:

(10)



(11)
由过程噪声和量测噪声的特性,易知S(k)为零均值的高斯随机量,其协方差阵为
(12)
其中,P(k|k-1)为预测误差协方差矩阵;R(k)为量测噪声V(k)的协方差矩阵。

从而,野值的判别式为:
(13)
其中,i,i表示矩阵对角线上的第i个元素;Si(k)表示S(k)的第i个分量;K是一个常数,根据实际物理背景确定。
因此,对于X、Y和Z三个坐标轴方向,野值的判别与剔除的数学表达式分别为:

(14)
3仿真分析
目标在X-Y平面内分别沿X轴和Y轴做匀加速直线运动,初始值X0=[0,10,2,200,15,-5]T,分别代表X轴的初始位移、速度、加速度和Y轴的位移、速度、加速度。传感器只能量测到位移信息,传感器观测的X轴和Y轴的位移信息受到了零均值高斯白噪声干扰,X轴和Y轴上的噪声方差分别为100 m和200 m,仿真时间间隔为0.2 s,总共仿真40 s,在第8 s、16 s和32 s加入[5 000 m, 4 000 m]、[8 000 m, 9 000 m]、和[9 000 m, 10 000 m]的野值。
从仿真图1-图3中可以看出:传感器在8 s、16 s和32 s的量测值中加入比较大的人工噪声,普通的Kalman滤波算法在野值附近具有大的扰动,并且,每出现一个野值,需要一定的时间进行收敛;而具有野值剔除功能的修正的Kalman滤波算法能够很好地进行野值检测并完全剔除野值,并且能够很好地跟踪目标,进而使测量数据的统计特性不受野值的影响。

图1 位置误差的仿真对比曲线

图2 位置误差的局部放大仿真对比曲线

图3 位置误差的仿真对比
4结论
针对雷达测量数据中的野值问题,本文从滤波算法的原理和工程实践的实际出发,提出了一种新的野值判别和处理算法。仿真计算表明,该算法简单易行,可以有效地识别野值,消除野值对滤波的不利影响,并且能够很好地跟踪目标,满足许可误差要求,具有较好的实际应用价值。
参考文献:
[1]王佳,王敏,徐晓辉.一种干涉仪数据斑点型野值修正方法[J].弹箭与制导学报,2013,33(2):106-108.
[2]赵当丽,翟慧生,胡永辉.基于自适应Kalman滤波的共视数据处理算法[J].计算机工程,2010,36(8):286-297
[3]LIUZH,WANGJF,WUY.KalmanfilteroutlierdetectionmethodsbasedonMestimation[C].Proceedingsofthe32ndChineseControlConference,2013:4652-4655.
[4]MUTAWAAlJ.Identificationoferrors-in-variablesmodelwithobservationoutliersbasedonminimum-covariance-determinant[C].ProceedingsoftheAmericanControlConference,Proceedingsofthe2007AmericanControlConference,2007.
[5]MARTINE,LIGGINSII.Distributedfusionarchitecturesandalgorithmsfortargettracking[J].ProceedingsoftheIEEE,1997,85(1):95-106.
[6]刘利生.外测数据事后处理[M].北京:国防工业出版社,1989.
[7]卢迪,姚郁,贺风华.一种抗野值的Kalman滤波器[J].系统仿真学报,2004,16(5):1027-1029.
[8]李景熹,王字,王树宗,等.观测值中野值的判别与处理方法仿真研究[J].微计算机信息,2006,22(5):75-79.
[9]祝转民,杨宜康,李济生,等.滤波工程应用问题分析及改进方法研究[J].宇航学报,2002,23(3):44-47.
[10]金学军.基于最小二乘拟合的外弹道测量数据野值剔除方法[J].四川兵工学报,2011,32(1) :20-23.
(责任编辑周江川)
One Method of Radar Data Restraining Outliers on Kalman Filter
ZHANG Ya-song, REN Hong-guang
(China Airborne Missile Academy, Luoyang 471009, China)
Abstract:In the actual filter processing of radar measurement data, the measured value with outliers will not only cause the measure error and the memory effect, but also make the filter system divergence, which effects the precision of result greatly. A method of distinguishing and rejecting outliers was presented, which was based on “innovation”, according to filter arithmetic principle and engineering practices. The result of simulation demonstrates that the method is easy to operate, and it can effectively eliminate the bad effect of outliers on filter and improve the measurement accuracy.
Key words:Kalman Filter; outliers rejecting
文章编号:1006-0707(2016)02-0045-03
中图分类号:TJ765.2
文献标识码:A
doi:10.11809/scbgxb2016.02.012
作者简介:张亚松(1979—),男,硕士,工程师,主要从事制导控制系统设计研究。
基金项目:航空科学基金(2013ZC12004)
收稿日期:2015-09-18;修回日期:2015-10-22
本文引用格式:张亚松,任宏光.一种基于Kalman滤波的雷达数据抗野值方法[J].兵器装备工程学报,2016(2):45-47.
【装备理论与装备技术】

