迫击炮座钣-土壤耦合发射动力学分析研究

周中佳，卜华涛，何　永

(南京理工大学 机械工程学院，南京　210094)



迫击炮座钣-土壤耦合发射动力学分析研究

周中佳，卜华涛，何永

(南京理工大学 机械工程学院，南京210094)

摘要：为研究某型迫击炮座钣在密实中硬土上发射过程中的结构强度问题，基于非线性有限元理论，建立了该迫击炮座钣与土壤耦合力学有限元模型，该模型考虑了土体本构模型、结构-土壤接触非线性关系；以静力学分析和动力学分析，得到座钣的应力分布规律以及座钣关键部位的动应力变化曲线；通过对比表明：相同条件下的两种加载方式，座钣的最大应力的位置基本一致，静力学分析的结果比动力学分析的结果大9%左右。计算与对比结果为对迫击炮座钣结构进一步优化提供参考依据。

关键词：迫击炮座钣；非线性有限元；土壤；接触

Citation format:ZHOU Zhong-jia，BU Hua-tao，HE Yong.Firing Dynamic Analysis of Coupling Mortar Base Plate-Soil[J].Journal of Ordnance Equipment Engineering,2016(2):18-21.

迫击炮是一种用座钣直接承受后坐力的曲射炮。座钣为迫击炮的重要组成部分。在射击时，后坐力通过座钣传递给土壤，通过控制土壤，保证迫击炮有良好的后坐稳定性和复进稳定性，可改善连续射击能力及射击精度和射击密集度。座钣结构设计的好坏，对迫击炮的战斗性有巨大影响。而在迫击炮座钣设计中，其强度、刚度应首当其冲考虑。

近几十年来，随着有限元法的重大发展，使得数值解法成功地应用于各种复杂结构的弹塑性问题并产生了相关计算力学。南京理工大学的马洪锋[2]应用非线性有限元理论和结构优化设计理论，研究迫击炮座钣置于刚性地面、中硬土地面的静态应力分析与结构优化设计；中北大学的柳云锋[3]采用有限单元法对某型迫击炮座钣进行瞬态动力学分析，得到整个座钣的结构应力和变形分布规律，以及座钣关键部位的动应力变化曲线；南京理工大学的赫信鹏[4]等人，对座钣用壳单元模型进行了动力学有限元分析，为座钣进行等强度，等刚度设计提供了理论依据。

纵观文献，将有限元法应用于迫击炮座钣结构的刚强度分析，已经取得相当大的成功。这对提高迫击炮的设计水平与缩短其研发周期具有重要意义。笔者在前人研究的基础上，基于非线性有限元理论，应用大型通用有限元软件ABAQUS，对某型号迫击炮座钣分别以静力学分析与动力学分析，模拟迫击炮发射时座钣与土壤耦合接触，得出两种分析状态下座钣的应力分布规律，从而进行对比分析，为迫击炮座钣结构进一步优化提供参考。

1座钣-土壤耦合模型的建立

1.1座钣与土壤模型的建立

迫击炮的一般射角为45°～85°，本文取一种常用的射角75°来研究。迫击炮发射时炮膛合力通过炮尾作用到座钣上，炮尾尾球通过接触座钣驻臼传递载荷。

张玉娥[5]通过计算与分析总结出：当有限元区域直径取到结构宽度的1.5倍以上时，可以满足精度要求，有限元区域直径的大小可以不再增加。土壤模型采用连续体有限元进行建模，直径取座钣直径的2.5倍，保证有限元区域大小与计算精度。座钣坑根据座钣背面的几何形状构筑，以便座钣放入后能与土壤很好贴合。

由于计算模型是对称的，在此取其1/2来建模。座钣与土壤装配的模型如图1所示。

图1　装配好的座钣与土壤模型

1.2座钣、土壤的材料属性

座钣的材料为钛合金，其弹性模量为108 GPa，泊松比为0.3，密度为4.62×103 kg/m3。

发射阵地的土质情况很复杂，一般都习惯于把迫击炮发射阵地的土质分为坚硬土、中硬土和松软土三类。发射阵地一般应选择较硬的土质，以减小迫击炮射击时的运动和座钣的下沉量。迫击炮射击时，座钣坑中的土壤已经被捣实，在开始发出几发炮弹后，土壤已经与座钣贴合，土已经被压实。基于以上，本文选取一种偏硬的密实砂土。

土体的应力应变关系很复杂，通常具有非线性、弹塑性、剪胀性和各向异性等。文中选线弹性模型模拟土壤的弹性变形阶段，用扩展的Drucker-Prager1模型模拟土壤塑性变形阶段。参考《工程地质手册》选取土壤参数(表1)。

为了更加真实的模拟迫击炮发射过程中座钣与土壤的接触受力情况，土壤应取其动弹性模量。与其他材料相比，地基土的动、静模量差别很大[8]，如对钢材，在常温时，Es=Ed；对钢筋混凝土结构：Es=Ed；对地基土，与地质的好坏有关，软土：Es≈0.125Ed，黏土Es=(0.2～0.3)Ed；基于以上，取密实砂土的动弹性模量为150 MPa。

表1　密实砂土的模型参数

1.3迫击炮发射时的受力分析

座钣置于中硬土发射时的受力情况如图2所示。图2中忽略了后座部分的重力和双腿架对后坐部分的作用力，迫击炮在中硬土上发射时座钣主要受到下面几个力的作用：Fpt为炮膛合力，FTN为土壤抗力的法向方向分力，FTT为土壤抗力的切向分力，Fgc为除座钣外的后座部分的惯性力，Fgb为座钣惯性力，φ为高低射角。

为了简化计算，假设后坐力质心在身管轴线上，后坐力F=Fpt，忽略Fgc和Fgb。

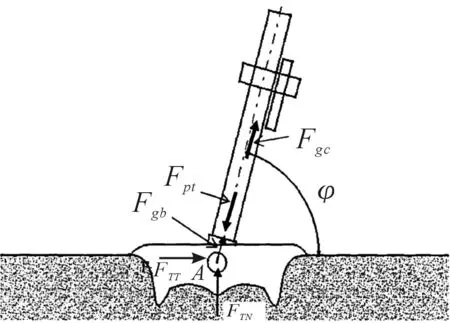
图2　座钣的受力示意图

1.4边界条件定义

由于只取一半的模型研究，所以在定义边界的时候，必须对模型中间面进行对称约束。土壤的下面和侧面对其进行固定边界约束，其约束好的模型如图3。

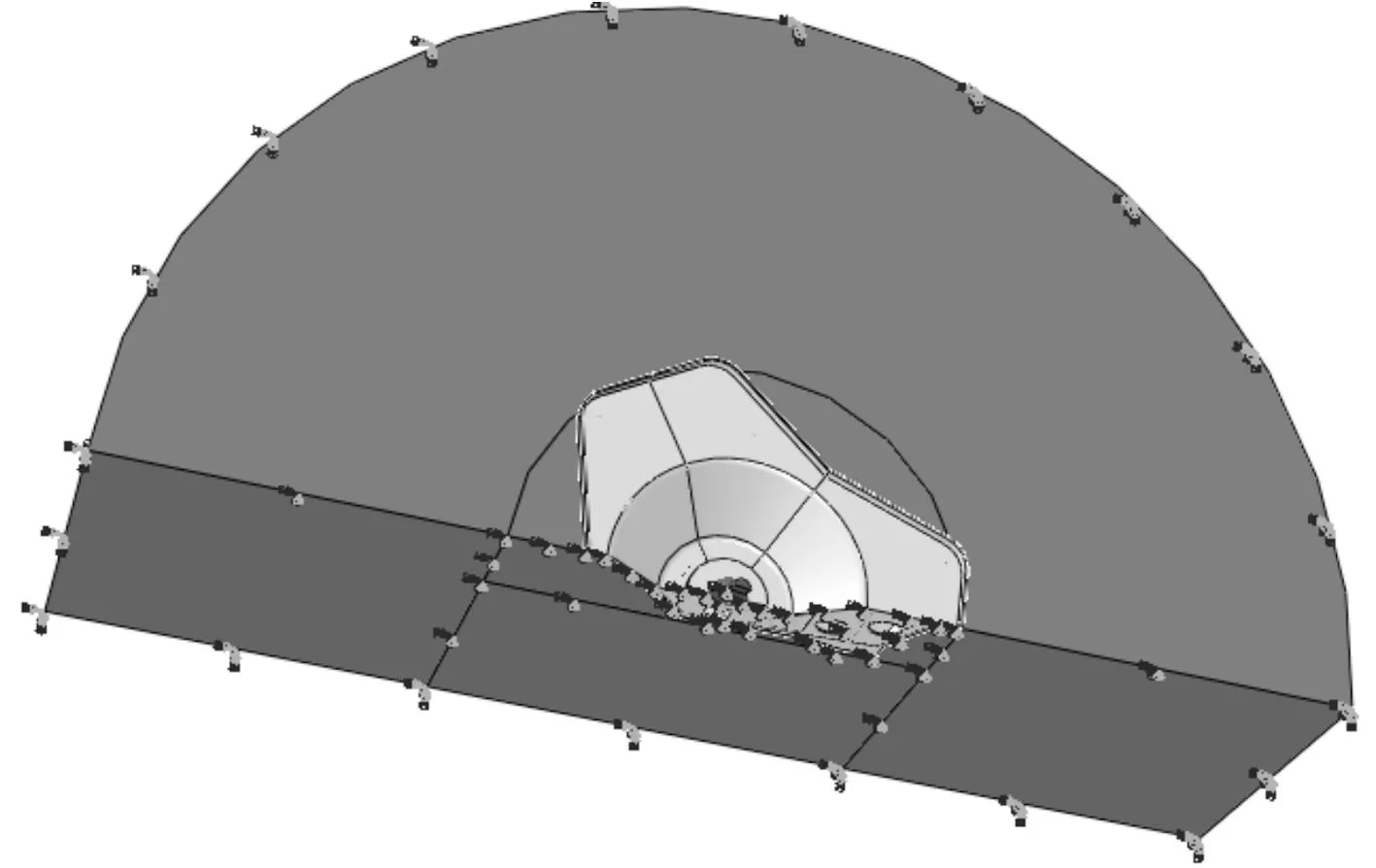
图3　约束的座钣与土壤模型

2座钣-土壤耦合力学分析

迫击炮发射过程中，伴随着瞬时、高能、强冲击行为，座钣与土壤耦合在一起，整个过程会呈现高度的非线性行为。

2.1静力学分析

在静力学分析中，为了使物体处于静态平衡，作用在每个节点上的静力必须为零。因此，静态平衡的基本判据是内部力I和外部力P必须互相平衡：

P-I=0

ABAQUS/Standard中应用Newton-Raphson算法获得非线性问题的解答。在非线性分析中，以增量施加给定的载荷求解，逐步地获得最终解答。

2.1.1接触的模拟

座钣与尾球在接触面上仅有法线方向的位移变化，两接触面之间切向相对位移量很小，为了简化加载模型，使用绑定约束模拟尾球与座钣之间的接触。

座钣与土壤的接触模型采用库伦摩擦模型，其摩擦因子取0.2。座钣陷入在座钣坑中，钣面与土壤紧密贴合，在接触部位以面对面接触分别建立了28对接触面。

2.1.2网格的选择

考虑到接触模型曲面的复杂性与精度的要求，土壤模型被分成3部分。在ABAQUS/Standard单元类型库下，与座钣相接触的土壤部分选择采用C3D10M(修正的二阶四面体单元)离散，其余部分以C3D8I(8节点六面体线性非协调模式单元)离散。划分网格后的土壤模型如图4所示。

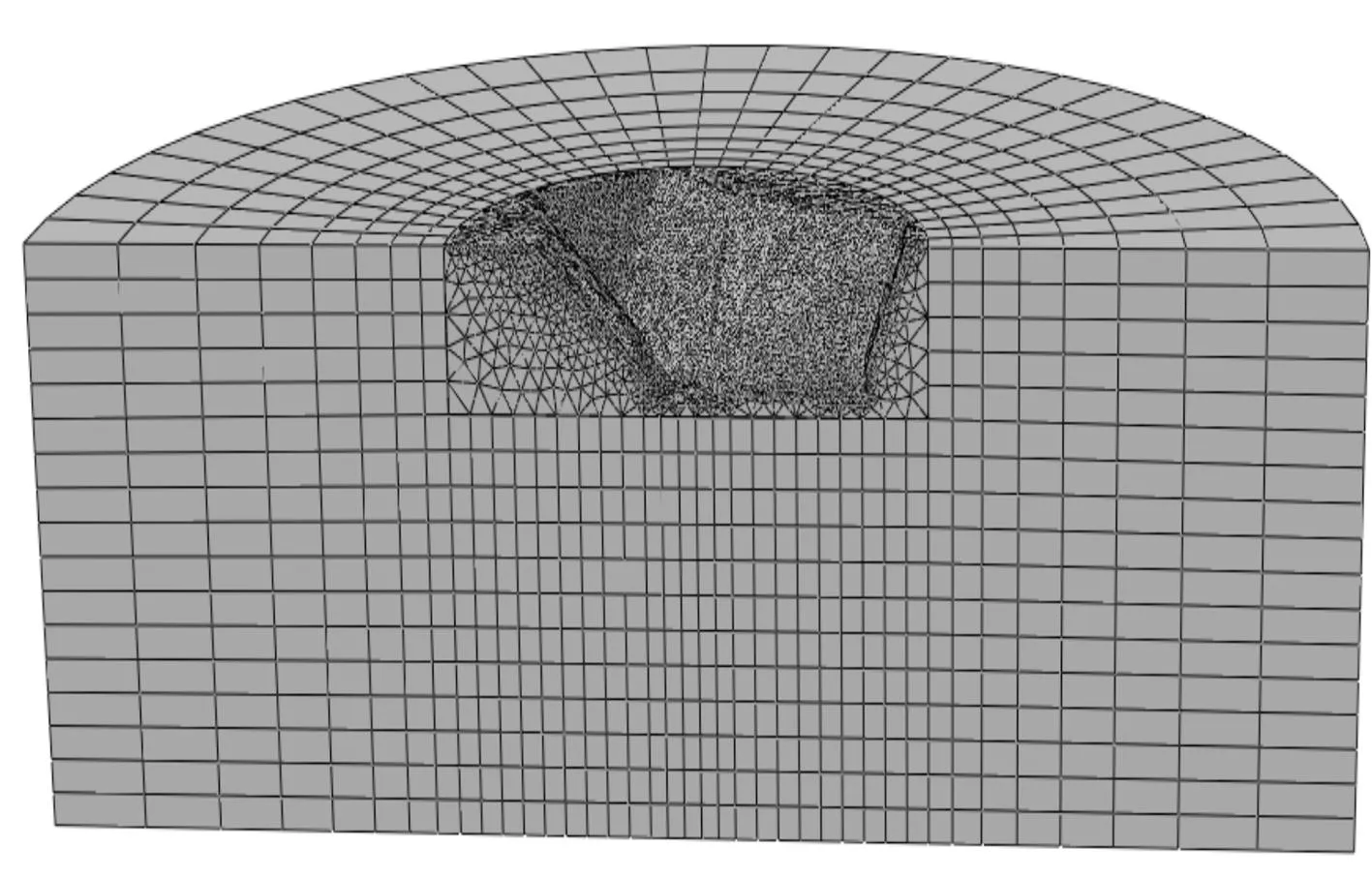
图4　划分网格的土壤

座钣的结构模型比较复杂，为了保证座钣的分析精度，采用C3D10M(修正的二阶四面体单元)离散，此单元能够模拟接触问题且有足够的精度。划分网格后的座钣如图5所示。

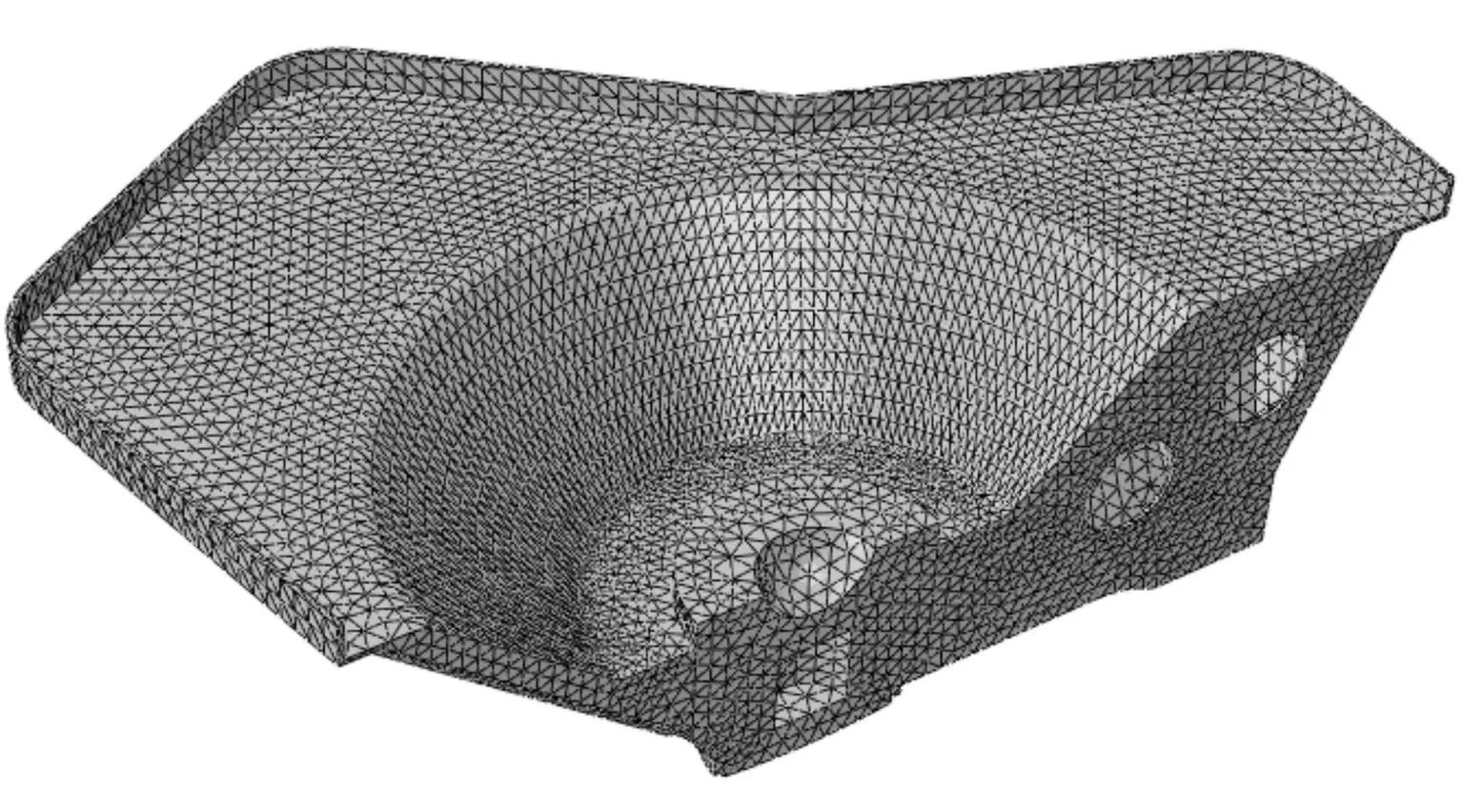
图5　划分网格后的座钣

2.1.3载荷

某型号的迫击炮最大炮膛合力为F=1 413 kN，折算成均布载荷施加到尾球上，模拟最大膛压下座钣承受瞬态载荷。

2.1.4计算结果

在75°射角的射击状态下，座钣的最大应力发生在靠近中心棱脊部位与筋钣的连接处，σmax=1 131 MPa。应力云图如图6、图7所示。

图6　整体应力云图

图7　最大应力处

2.2动力学分析

动力学分析是将惯性力包含在动力学平衡方程中：

其中，M是结构的质量；ü是结构的加速度；I是结构中的内力；P是所施加的外力。

ABAQUS/Explicit运用中心差分法，从上一个增量步显式地推出动力学状态而无需进行迭代，确定了动平衡方程P-I﹦Mü，获得非线性解。

2.2.1接触的模拟

尾球与座钣之间使用绑定约束模拟接触。座钣与土壤之间的接触模型采用库伦摩擦模型，其摩擦因子取值为0.2。接触部位采用通用接触算法，这种算法通常让ABAQUS/Explicit自动生成包含所有实体的定义接触面。

2.2.2网格的选择

考虑计算精度与ABAQUS/Explicit中稳定极限与最短单元尺寸之比，将土壤分为3个部分，与座钣相接触的地方采用尽可能均匀的C3D10M(修正的二阶四面体单元)进行离散，其余部分用C3D8R(8节点六面体线性减缩积分单元)离散。

座钣的结构比较复杂，采用C3D10M进行离散，在应力集中部位进行适当的网格加密。如图8所示。

2.2.3载荷

某型迫击炮的实际膛压曲线如图9所示，载荷历程为10 ms。为了简化计算，将后坐力设为随时间变化的均布面压力。

2.2.4计算结果

在75°射角的射击下状态下，座钣的最大应力发生在t=4.16 ms左右，靠近中心棱脊部位与筋钣连接处，σmax=1 036 MPa。应力云图如图10、图11、图12所示。

图8　划分网格后的座钣与土壤的装配图

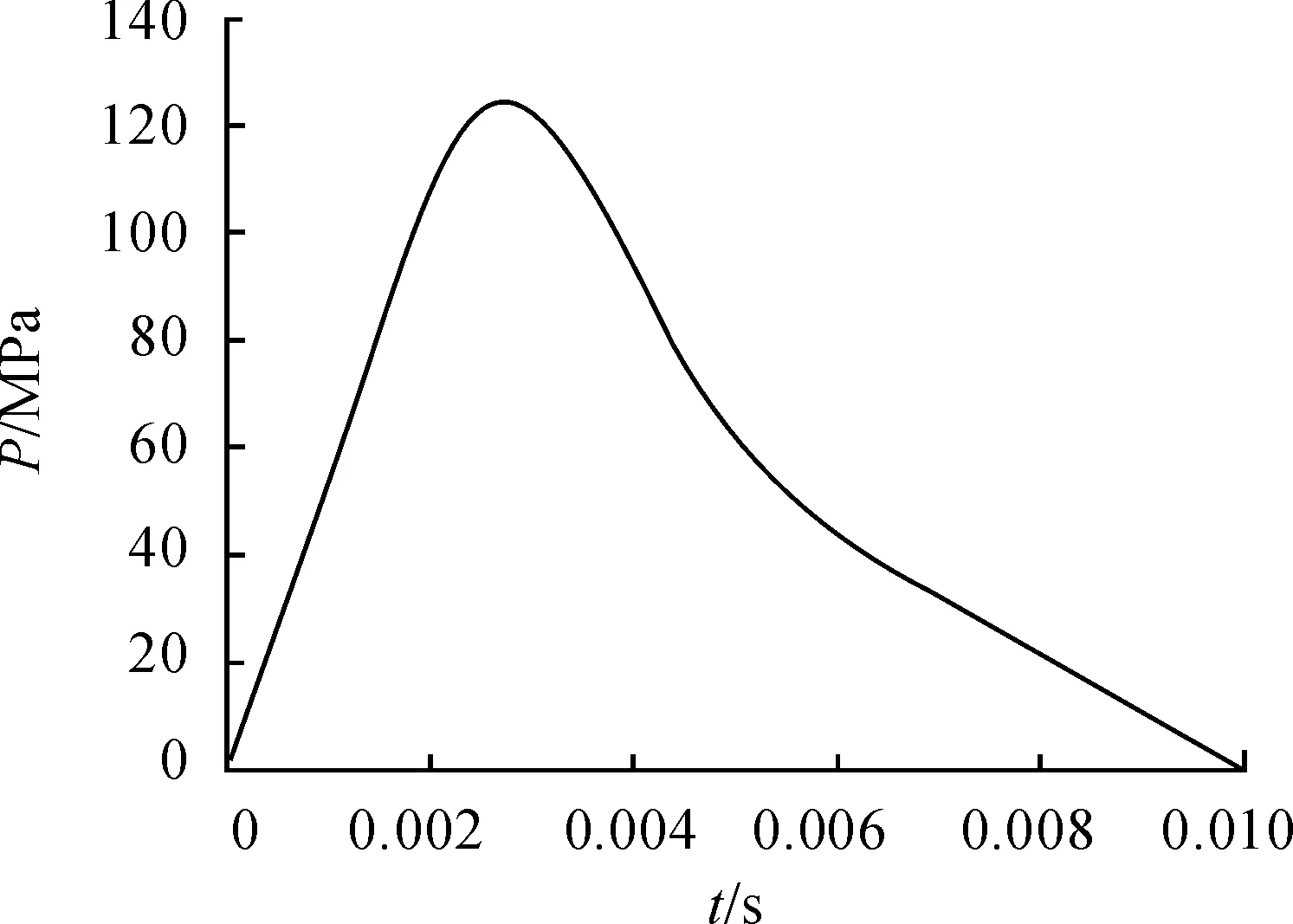
图9　迫击炮的膛压曲线

图10　t=4.16 ms，座钣正面应力云图

图11　t=4.16 ms，座钣最大应力处

2.3静力学与动力学对比分析

由以上的计算结果可以表明：座钣的最大应力发生的位置均在靠近中心棱脊部位与筋钣的连接处，静力学分析的应力结果比动力学分析的结果大9%左右。这是因为，在静力学和动力学分析之间最主要的区别是在平衡方程中是否包含惯性力(Mü)。在两类模拟之间的另一个区别在于内力I的定义。在静力学分析中，内力仅由结构的变形引起；而在动力学分析中，内力包括了运动(例如阻尼)和结构变形的共同贡献(表2)。

图12　最大应力点处随时间变化的应力曲线

分析方式最大应力位置最大应力值/MPa静力学分析中心棱脊部位与筋钣的连接处1131动力学分析中心棱脊部位与筋钣的连接处1036

3结束语

笔者在研究某型迫击炮座钣与土壤的耦合接触非线性有限元的建模方法基础上，以数值计算的方法得到了座钣在静力学分析和动力学分析下的应力分布规律，找出座钣等效应力分布最大的位置。计算结果表明，同等情况下的动力学分析的结果小于静力学分析的结果。通常情况下，由于动态分析中考虑了座钣的惯性力，分析结果往往会小于静态分析的结果。静态分析的结果偏保守，而动态分析得出的结果更接近于真实受力情况。

参考文献：

[1]唐治.迫击炮设计[M].北京：兵器工业出版社，1994.

[2]马洪锋.迫击炮座钣的结构分析与优化设计[D].南京：南京理工大学，2009.

[3]柳云峰.基于AWE某迫击炮座钣瞬态动力学分析[J].机械工程与自动化，2011(3)：41-42.

[4]赫信鹏.迫击炮座钣动态特性分析[J].南京理工大学学报，1993(5)：55-59.

[5]张玉娥.分析范围对地下结构无限元动力响应的影响[J].铁道建筑,2006(8)：42-45.

[6]费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2013

[7]常士骠，张苏民.工程地质手册[M].4版.北京：中国建筑工业出版社，2008.

[8]徐建.建筑振动工程手册[M].北京：中国建筑工业出版社，2002.

[9]赵腾伦.ABAQUS6.6在机械工程中的应用[M].北京：中国水利水电出版社，2007.

(责任编辑周江川)

Firing Dynamic Analysis of Coupling Mortar Base Plate-Soil

ZHOU Zhong-jia，BU Hua-tao，HE Yong

(School of Mechanical Engineering, Nanjing University of Science & Technology, Nanjing 210094, China)

Abstract:In order to study the strength of mortar base plate on the mid-hard soil during firing, a coupling nonlinear finite element model of mortar’s base plate and hard soil was built based on the nonlinear finite element theory. The nonlinear relations of soil constitutive model and interaction between structure and soil were considered simultaneously in the model. The stress distribution law and the dynamic stress curves of mortar base plate were calculated in the static analysis and dynamic analysis. By the comparing, it shows that the position of the maximum stress is similar in the same condition and the stress of static analysis is 9% larger than the dynamic analysis. The result provides a reference to the further optimization of mortar base plate structure.

Key words：mortar base plate；nonlinear finite element；soil；interaction contact

文章编号：1006-0707(2016)02-0018-04

中图分类号：TJ31

文献标识码：A

doi:10.11809/scbgxb2016.02.005

作者简介：周中佳(1988—)，男，硕士研究生，主要从事火炮结构动力学研究。

收稿日期：2015-06-24；修回日期：2015-07-15

本文引用格式：周中佳，卜华涛，何永.迫击炮座钣-土壤耦合发射动力学分析研究[J].兵器装备工程学报，2016(2):18-21.

【装备理论与装备技术】