基于整车误用工况的发动机悬置支架结构优化研究
郭绍良,李进超,熊 飞,周鑫美,李玉发
(广州汽车集团股份有限公司汽车工程研究院,广州 511434)
2016191
基于整车误用工况的发动机悬置支架结构优化研究
郭绍良,李进超,熊 飞,周鑫美,李玉发
(广州汽车集团股份有限公司汽车工程研究院,广州 511434)
某款乘用车在开发过程中,发动机悬置支架在整车误用试验工况下发生断裂。通过对断口进行宏观分析,初步判断悬置支架系因误用工况下承受载荷过大而发生快速断裂。本文中通过建立整车车辆动力学模型,以模拟误用试验工况,获取悬置支架的载荷并进行结构强度校核。分析结果显示该工况下,悬置支架强度不满足要求且分析结构危险位置同试验实际发生断裂位置一致。最后,基于该误用工况和悬置强度校核常用的28种工况对悬置支架进行拓扑优化设计,制作优化设计方案样件经过搭载实车试验没有发生断裂。本文的研究,为发动机悬置支架的强度性能设计提供了重要的参考。
发动机悬置支架;车辆动力学;有限元分析;拓扑优化
前言
动力总成是汽车的主要振源之一,悬置系统作为连接动力总成和车架之间的重要零件,除了要在各个工况下支撑动力总成,还需要良好的隔振性能。悬置系统一般包括橡胶衬套和金属支架,金属支架起支撑动力总成并传递振动的作用,而橡胶衬套主要起隔振作用[1]。金属支架对振动的传递有重要影响,因此金属支架的刚度和模态都要满足一定要求。金属支架对动力总成起支撑作用,需要足够的强度,在动力总成一些极端工况时,仍能提供足够的支撑,而不会发生断裂。
在悬置系统的开发过程中,需要对悬置支架的强度进行校核。行业内使用较多校核悬置支架的工况有28种[2],如表1所示。在开发某款乘用车的悬置系统时,悬置支架结构如图1所示,该支架经过28种工况的校核没有问题,而在整车误用试验中发生如图2所示的断裂。观察支架的断口如图3所示,无明显疲劳辉纹,整个断裂以快速断裂为主,螺栓孔附近的断面能看到“人”字花纹样,并指向断裂源。断口组织细密,未发现明显的夹砂、缩孔和气孔等铸造缺陷,并对悬置支架化学成分检测如表2所示,满足JIS H5302—2000标准对材料ADC12的要求,故初步判断断裂原因为悬置支架承受过大的载荷[3]。
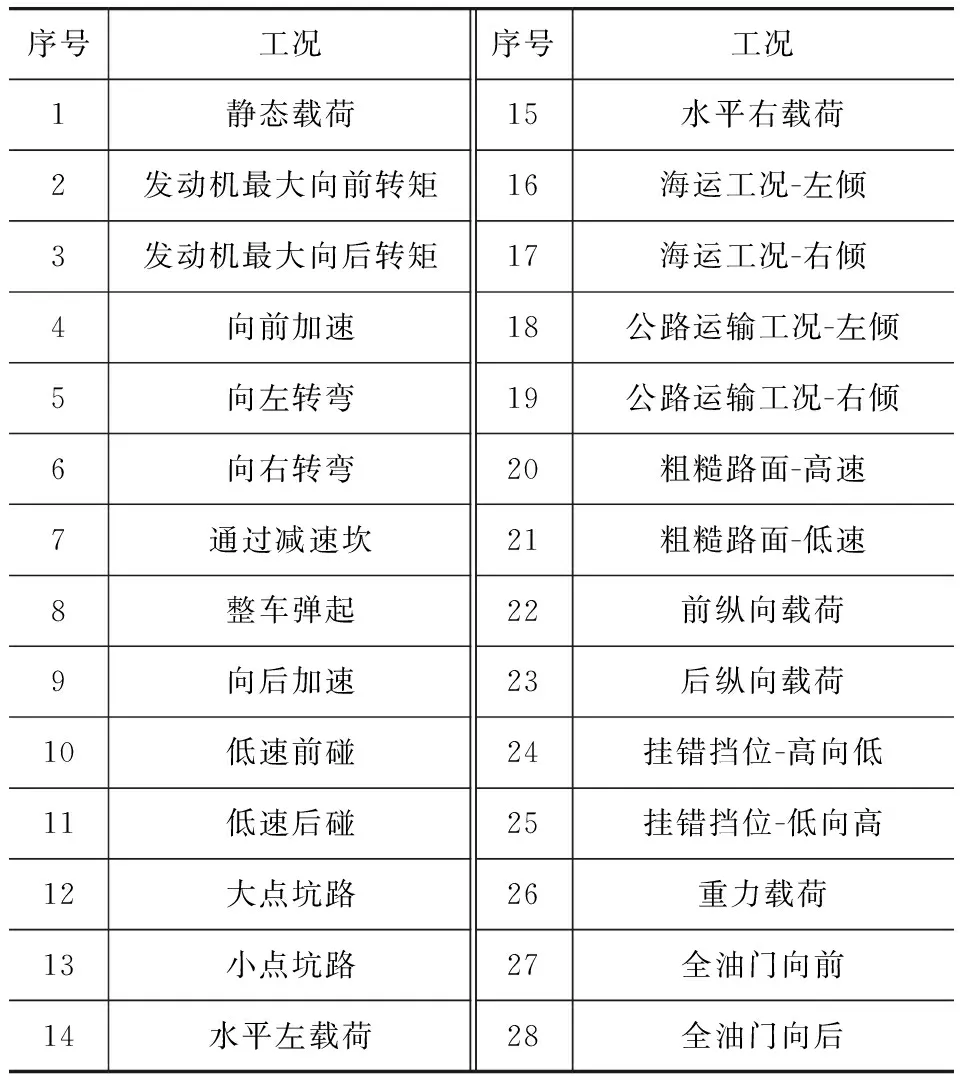
表1 动力总成悬置系统工况
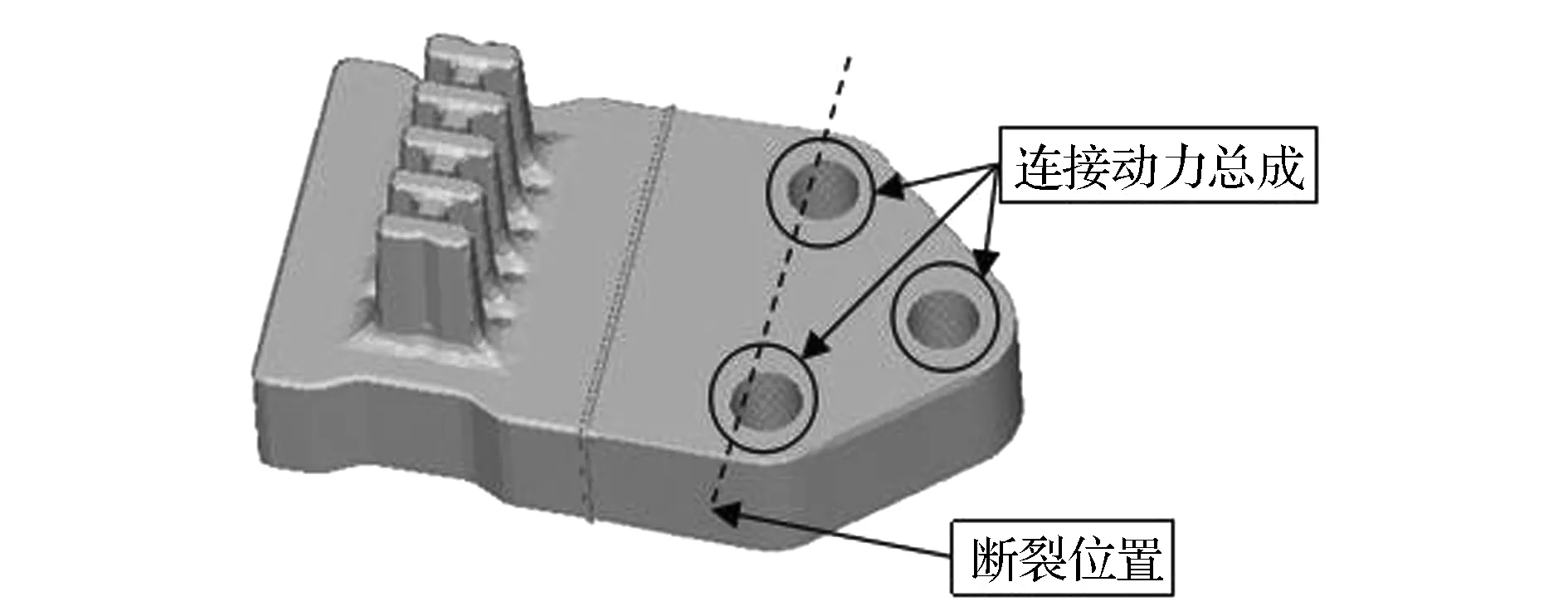
图1 悬置支架

图2 断裂的悬置支架

图3 支架断口

%
本文中以悬置支架断裂的整车误用工况为出发点,认为除了通过28种工况进行悬置支架校核外,还需根据整车实际的使用工况,增加对悬置支架的校核。通过建立整车车辆动力模型开展误用试验工况模拟分析,获取该工况的载荷来校核悬置支架,并进行相应的优化,以解决悬置支架断裂问题,为后续车辆悬置设计开发积累宝贵经验。
1 动力学误用工况模拟与载荷获取
1.1 整车仿真模型建立
为建立适合本文中进行整车误用工况模拟的多体模型,在Adams/Car中里建立整车动力学仿真分析模型,再在Adams/View中建立相应的障碍物和碰撞约束,驱动车辆以一定的速度通过障碍物,分析动力总成左悬置的受力。
在Adams/Car中建立整车模型,包括前后悬架系统、车身、动力总成、转向系、制动系和轮胎等子系统,每个子系统都按照实车的硬点、质量和转动惯量等物理参数建模,其中发动机和变速器控制策略采用实际ECU策略建模。整车模型及实车如图4所示,其中前悬架为双叉臂独立悬架,后悬架为多连杆独立悬架。

图4 整车动力学仿真模型及实车
根据实车试验通过的障碍物尺寸在Adams/View中建立相应障碍物,如图5所示。该障碍物为一斜坡,车辆以一定的速度驶上斜坡,并继续向前行驶,建立路面与车辆底盘的接触以获得接触碰撞力。
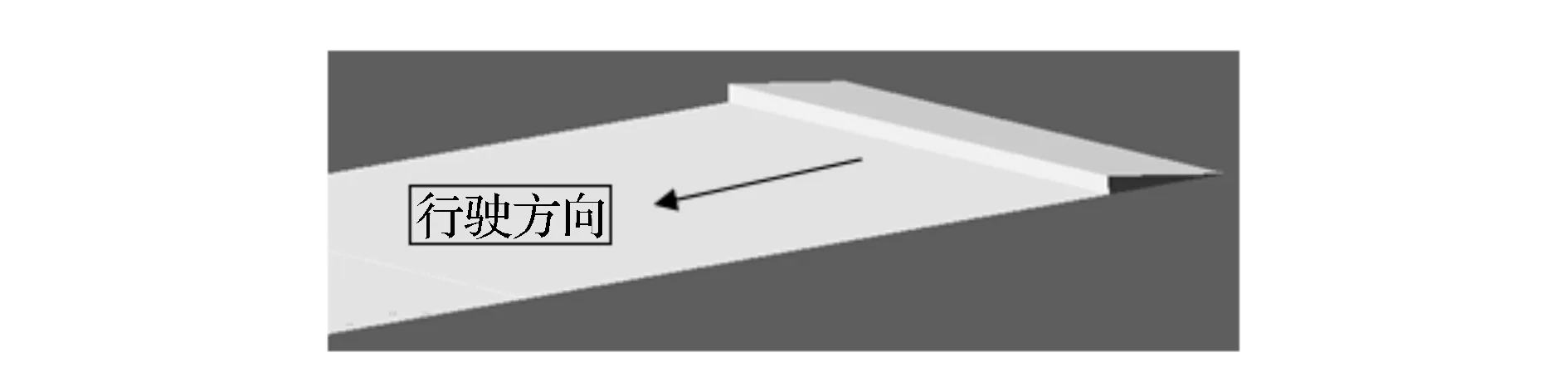
图5 路面
1.2 整车仿真模型验证
由于整车模型为全物理参数建模,为验证整车仿真模型的准确性,本文中采用与样车操稳试验数据对照的方法对模型进行标定和校验,通过仿真模型计算结果与实车试验数值的对比分析,证实仿真模型的有效性,使其达到此次研究所要求的精度。
根据研究需求选择稳态定半径(转向盘左转)试验进行整车模型验证,试验测试如图6所示。稳态定半径工况代表车辆一种稳定的转弯状态,车辆以固定的转弯半径转弯行驶,车速逐渐增加到达最大侧向加速度为止。该工况代表了车辆的基本操纵性能,主要反映车辆稳态响应特性。 稳态定半径一般选取车辆稳态不足转向度和稳态侧倾梯度为评价指标。稳态侧倾梯度用车身侧倾角同侧向加速度曲线的斜率来表示,如图7所示。稳态不足转向度用转向盘转角同侧向加速度曲线斜率来表示,如图8所示。通过图7和图8对比结果可以看出整车操稳仿真和试验曲线较一致,验证了模型的准确性。

图6 试验传感器的安装
1.3 仿真分析结果
在Adams/View中控制车辆以50km/h的车速通过斜坡,仿真结果显示,车辆通过斜坡后前轮先着地后,向前行驶了一小段距离,同时车身继续向下俯冲,由于车身前倾较大,前副车架与地面发生碰撞,如图9所示,经检查实车说明仿真结果与试验结果一致,如图10所示。
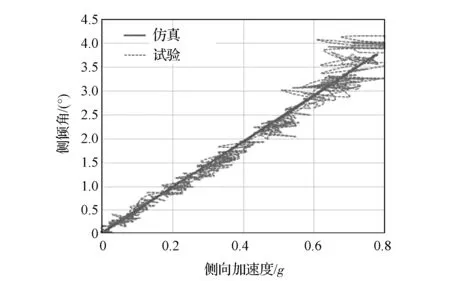
图7 稳态侧倾梯度
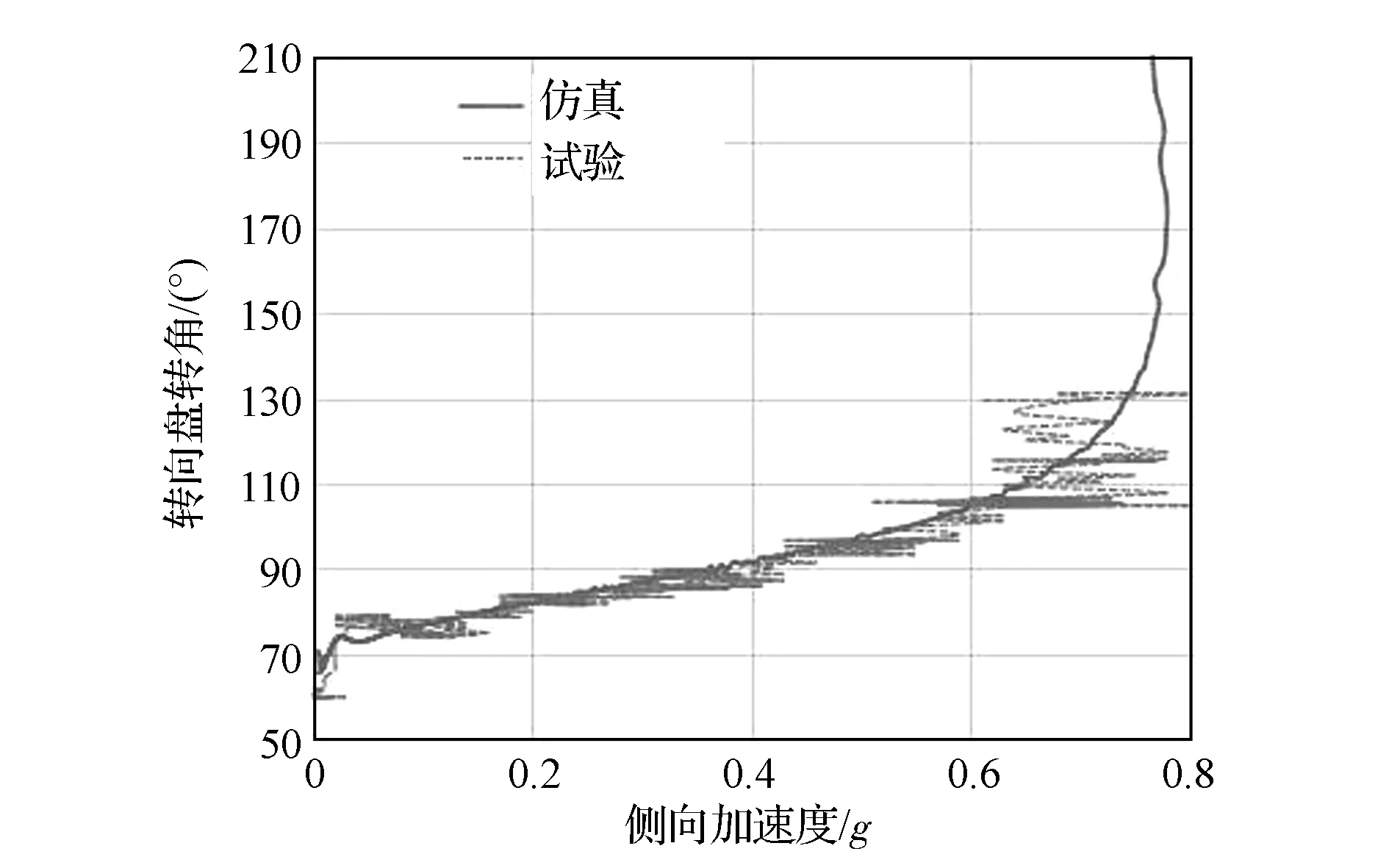
图8 稳态不足转向度
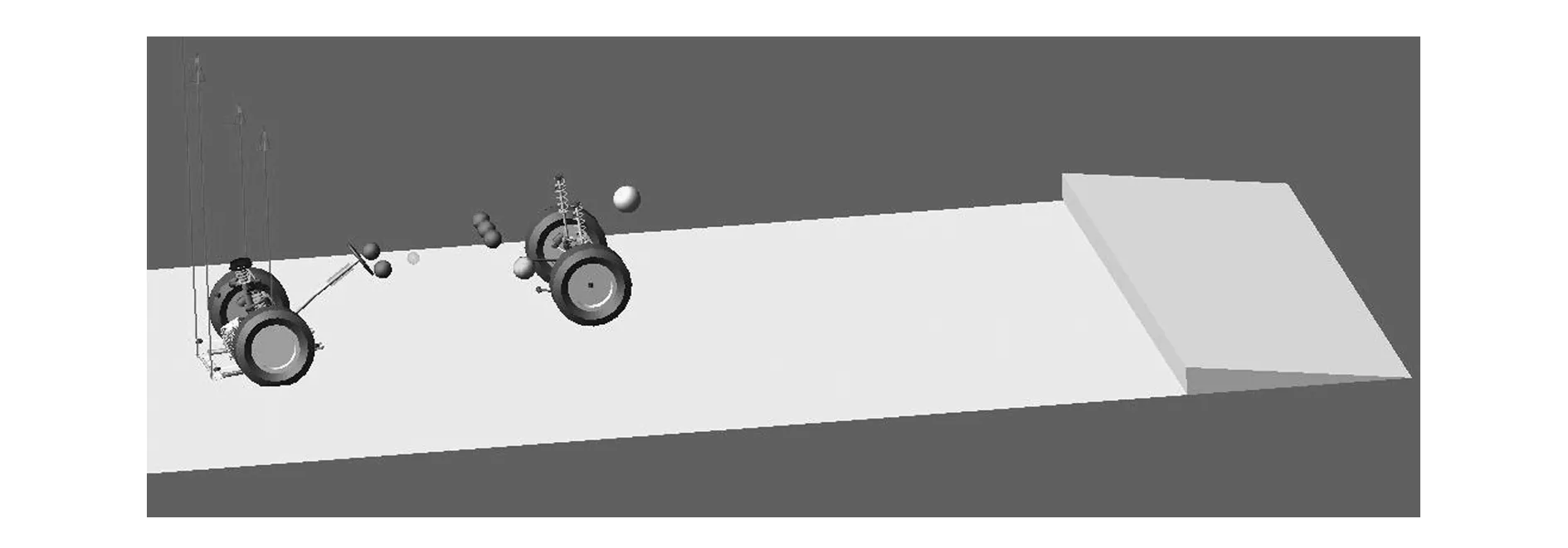
图9 左悬置受力最大时刻

图10 试验情况
在这个过程中,左悬置所受的垂向力如图11所示。第1个较大的波峰,左悬置受17kN的力,这是车辆冲上斜坡时产生的;第2个波峰左悬置受38kN的力,是车辆落地后前副车架与地面发生碰撞时车身产生较大的加速度,由于动力总成的惯性力,此时悬置受力最大。

图11 左悬置垂向力受力图
2 拓扑优化设计
2.1 拓扑优化数学模型
结构拓扑优化包括连续体结构和离散结构的拓扑优化。连续体拓扑优化的主要方法是将设计区域划分成有限单元,根据一定的算法将一部分区域删除,形成带孔的连续体,以实现拓扑优化。连续体的结构拓扑优化目前应用较多的是变密度法、均匀化法和渐进结构优化方法[4]。拓扑优化在汽车零部件的设计中使用较多,可避免传统优化时的盲目性,并减少重复建模的工作量,可快速找到优化方案。
本文中应用的是变密度法。变密度法以每个单元的相对密度作为设计变量,基于材料的各向同性,以连续变量密度函数的形式表达单元相对密度与材料弹性模量之间的关系,这种函数关系是人为假定的,程序实现简单,计算效率高。
变密度中常用的差值模型有固体各向同性惩罚微结构模型(solid isotropic microstructure with penalization,SIMP)和材料属性的合理近似模型(rational approximation of material properties,RAMP)。本文中采用SIMP模型,通过引入惩罚因子对中间密度值进行惩罚,使中间密度值向0和1两端聚集,以得到较好的优化结果。在给定的位移边界与载荷条件下,线弹性结构基于SIMP方法的拓扑优化模型[5-6]为
设材料模型为
ρ(x)=xeρ0
(1)
(2)
则拓扑优化模型为
(3)

(4)
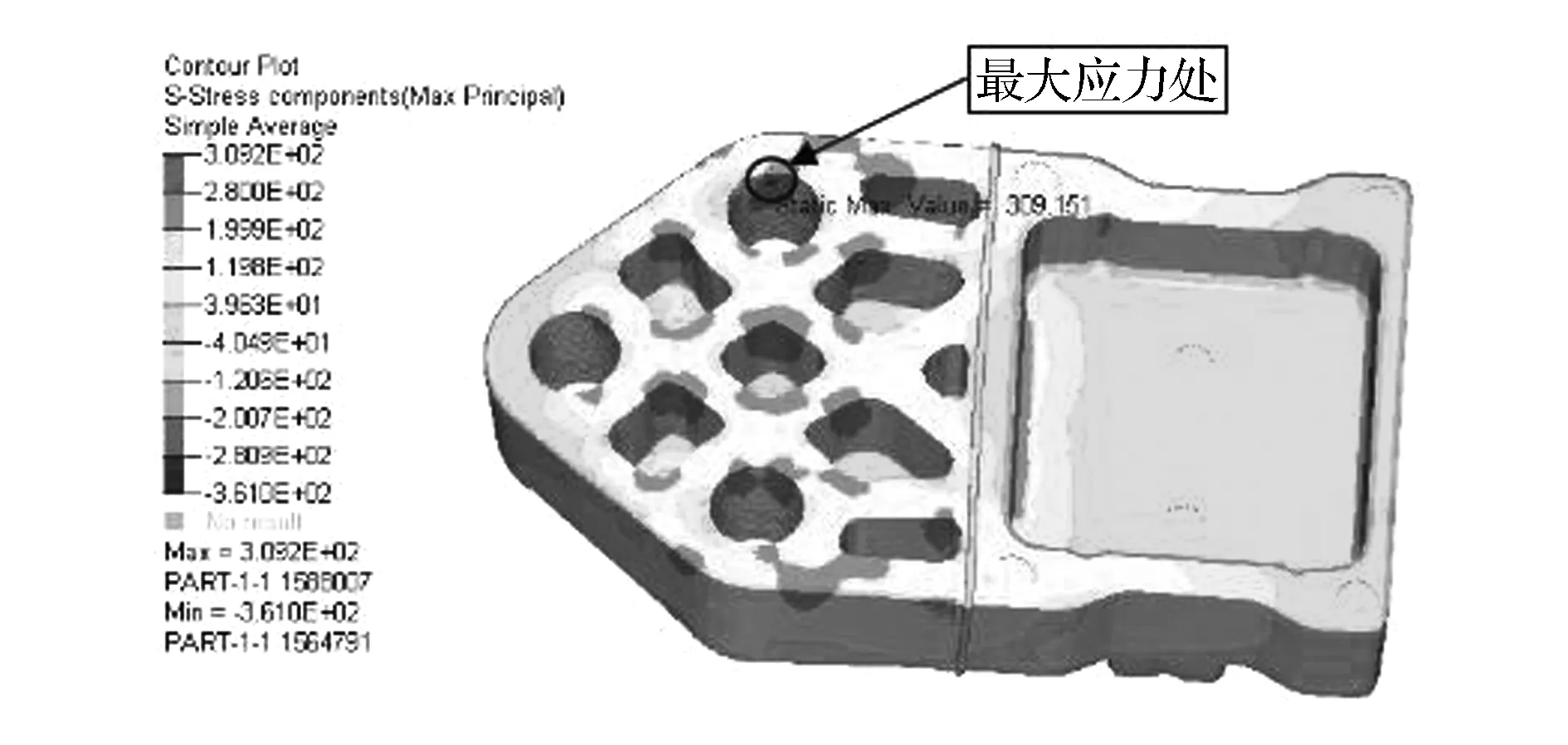
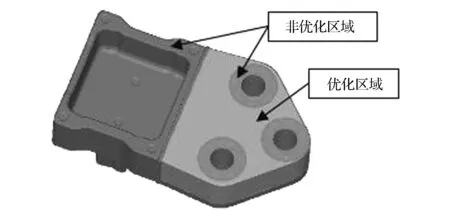
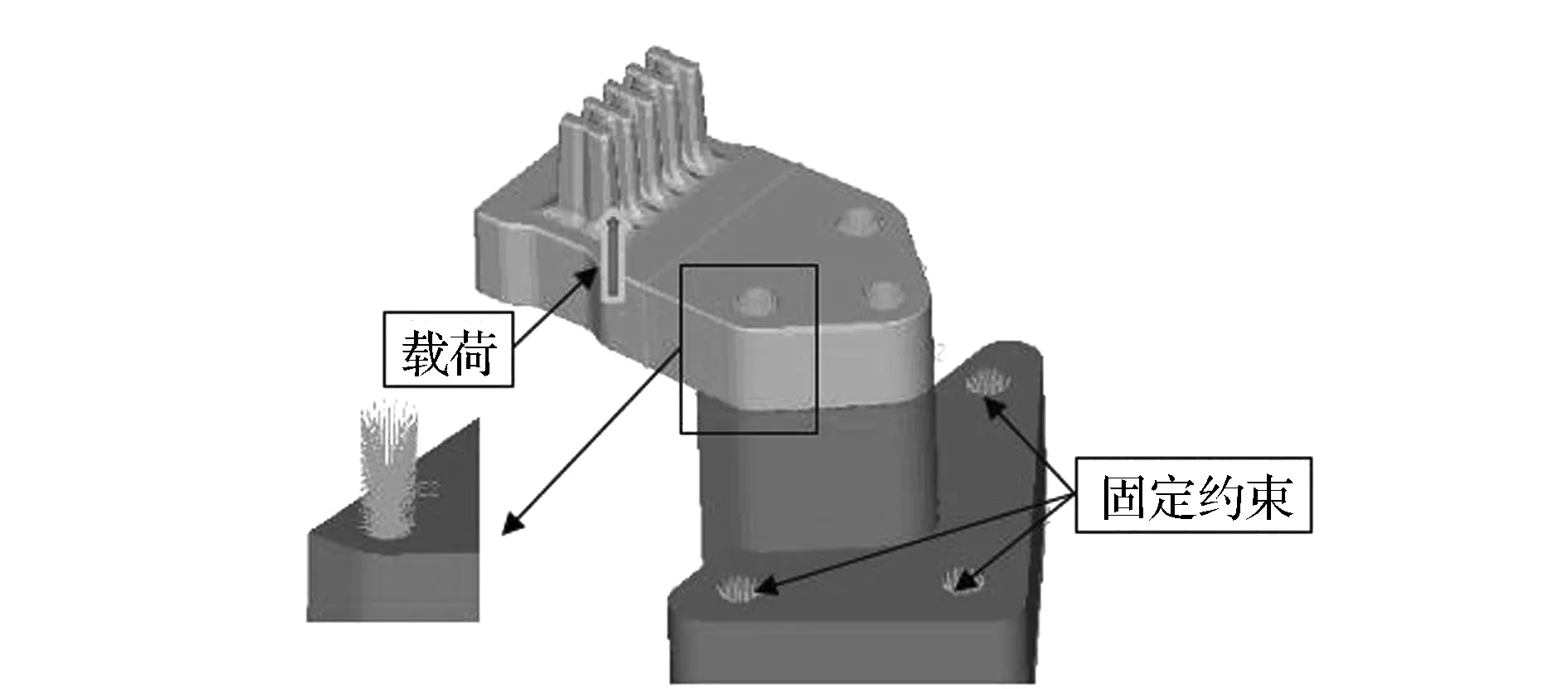
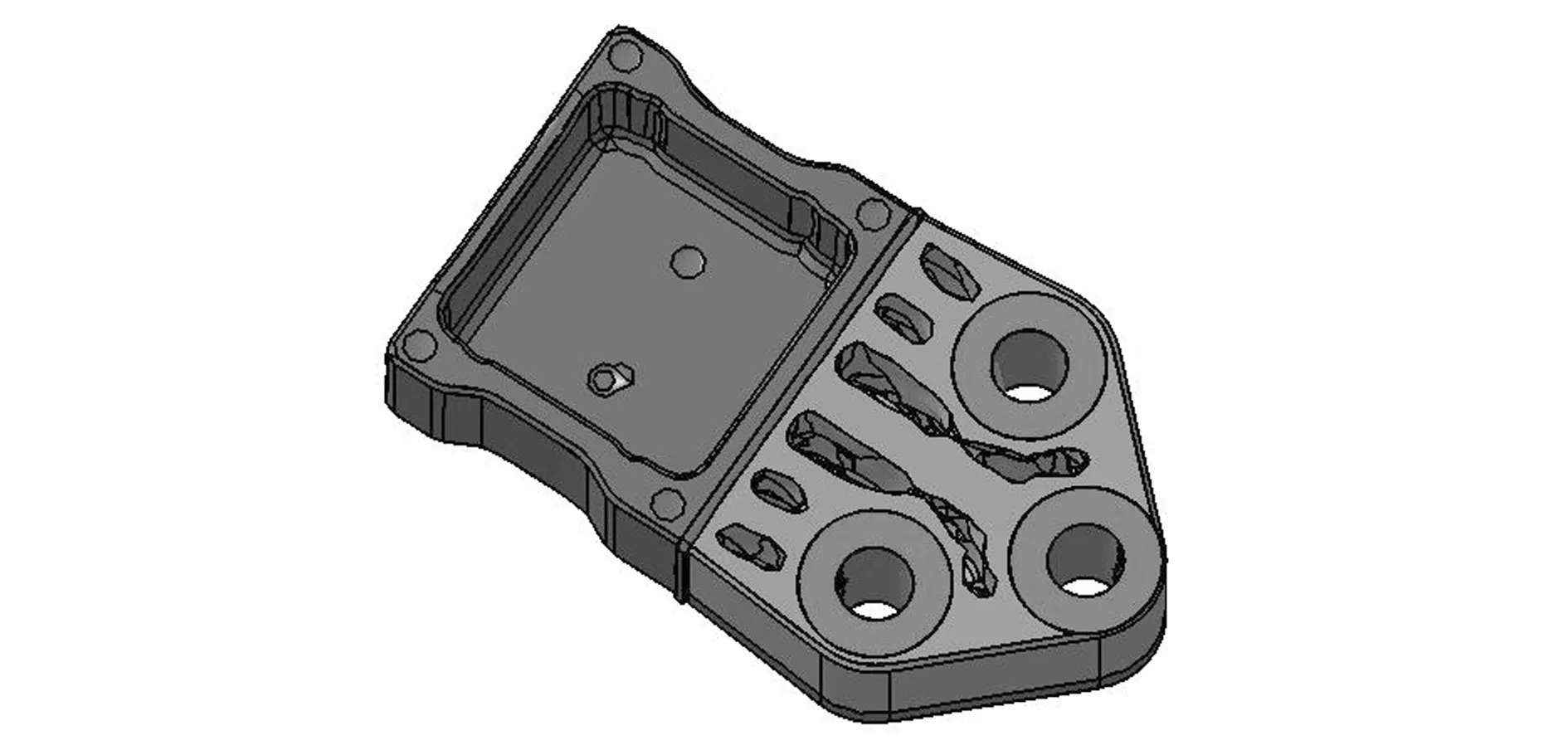
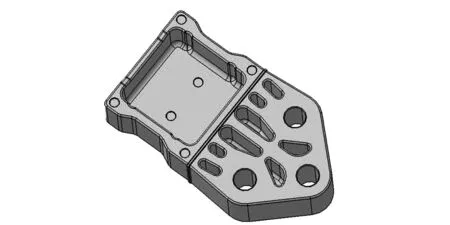
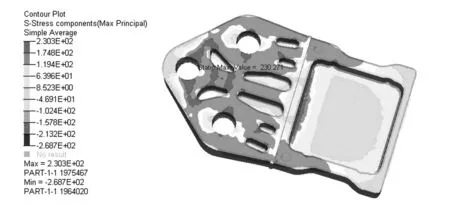
KU=F(0 (5) 式中:ρ和ρ0为均质实体密度、均质实体的密度矩阵;E和E0为均质实体弹性模量、均质实体的弹性矩阵;C(x)为结构总柔度;U和F为位移矢量、力矢量;k0和K为单元刚度矩阵、总体刚度矩阵;ue为单元位移矢量;xe,xmin和xmax为单元的相对密度、单元密度下限(取0.01)、单元密度上限(取1);V0,ve和Vaim为结构初始体积、优化后单元体积、优化后结构体积,m3;Vmax为体积约束条件;p为惩罚因子;N为结构离散单元总数;f为优化体积系数。 变密度法以单元的相对密度xe为拓扑优化设计变量,把结构的拓扑优化问题转换为求解材料的最优分布问题。在选择拓扑优化算法时,由于优化准则算法收敛速度快,迭代次数少,而且适用于复杂模型,故本文中应用优化准则算法求解SIMP的数学模型。 2.2 原方案强度校核 根据悬置支架的边界条件和载荷,建立悬置支架的有限元模型。由于悬置支架与动力总成支架接触,并通过螺栓压紧到一起,且本文中悬置支架开裂位置为螺栓孔附近,为得到较准确的螺栓孔附近的应力,故不能采用刚性单元代替螺栓来连接两个支架,本文中通过建立螺栓的实体模型进行分析,以得到螺栓孔附近的准确应力结果。螺栓采用六面体单元建模,单元类型为C3D8,3个螺栓共5 685个单元。悬置支架采用2阶四面体单元,单元类型为C3D10,划分成66 397个单元。螺栓、悬置支架和动力总成支架之间建立接触关系,并在螺栓内部施加预紧力。在动力总成支架的3个螺栓孔上建立固定约束,并在悬置中心点加载载荷,如图12所示。需建立2个载荷步,第1个载荷步先施加3个螺栓的预紧力,把悬置支架压紧到动力总成支架上;第2个载荷步再施加误用工况悬置支架的载荷。 图12 有限元建模 计算结果如图13所示。该工况下最大应力309MPa,材料断裂强度为253MPa,故该工况下悬置支架存在断裂风险。应力最大处位于螺栓孔内侧边缘,对比图3可知,应力最大处与断口分析断裂源位置相一致。可见整车动力学仿真模型对该工况的仿真及有限元计算与试验结果相一致,基本找到悬置断裂的原因。 图13 强度分析结果 2.3 拓扑优化 通过整车动力学仿真误用工况和有限元强度分析,确定了悬置支架断裂的原因,由于载荷过大,悬置支架螺栓孔附近强度不足,超过材料断裂强度,故需对悬置支架进行优化,本文中采用变密度法进行拓扑优化。在Hypermesh的Optistruct模块中实现拓扑优化,其中需定义3个优化要素:设计区域、目标函数和约束条件。 拓扑优化对设计区域的选择是比较敏感的,优化区域的设置会直接影响到优化的结果。在空间允许的前提下,应尽量选择较大的设计区域。故把悬置支架的有孔区域进行填充,如图14所示。因橡胶硫化区域不进行变更,螺栓孔附近为保证螺栓压紧时有良好的接触效果,故两个部分定义为非优化区域。 图14 优化区域定义 进行拓扑优化时,根据零部件的具体工艺和其他要求,需要考虑优化后零件的工艺性,保证零部件工艺的可行性[7]。悬置支架采用铸铝工艺,需考虑零件的最小和最大结构尺寸、对称、拔模的角度和方向等,故悬置支架拓扑优化模型设置[8-9]如下。 优化目标:悬置支架柔度最小。 优化约束:优化区域的体积分数<60%,最大应力<220MPa。 制造约束:最小单元尺寸>4mm,拔模方向为整车Z轴负向。 拓扑优化的有限元模型如图15所示,对动力总成支架的3个螺栓孔进行固定约束,悬置支架与动力总成支架之间通过刚性单元rbe2进行连接,在悬置支架弹性中心施加载荷38kN[10]。 图15 拓扑优化模型 在Hypermesh的Optistruct模块中对拓扑优化模型进行求解,得到伪密度为0.6~1.0的云图,可根据图16进行悬置支架的详细设计。 图16 0.6以上伪密度云图 2.4 优化结果分析 基于图16拓扑优化伪密度云图,对悬置支架进行结构重新设计,如图17所示。然后对该支架进行整车误用工况的强度校核,最大应力230MPa,如图18所示,小于材料抗拉强度,满足设计要求。 图17 重新设计的悬置支架 图18 优化后的强度分析结果 为较全面地校核优化后的悬置支架强度性能,再次用28工况进行强度分析,结果如表3所示。最大应力为68.7MPa,比整车误用工况最大应力小很多,再次验证28工况不能代表所有的汽车使用工况,而整车误用工况作为补充,对悬置支架的强度提出更高的要求,同时验证了拓扑优化后的悬置支架满足28工况的强度要求。 表3 28工况分析结果 MPa 3.1 台架试验验证 台架试验可在较短的时间内验证零部件的部分性能,并可控制试验环境,且便于控制试验进度和观察试验结果。故悬置支架设计完成后,先进行台架耐久试验。其中Z向耐久试验台架如图19所示,经过台架试验验证,悬置支架无开裂发生,说明悬置支架满足基本的耐久性能。 图19 悬置支架台架试验 3.2 整车道路试验 除了做零部件级别的台架试验外,还需将零部件搭载到整车上进行整车可靠性试验。整车可靠性试验由多种路面组成,其中一部分路面如图20所示。此外,整车还需要做驱动耐久试验,这个试验主要考察动力系统。试验中包含一些极限工况,同时这也是对悬置支架的强度和耐久性能的考察。 图20 部分道路试验路面 为验证拓扑优化的新结构的强度性能,装配优化后的悬置支架再次进行整车误用试验,如图21所示。试验验证悬置支架无断裂,说明整车动力学模型的仿真和拓扑优化设计是有效的。 图21 整车误用试验 本文中从悬置支架断裂的实际工况出发,用车辆动力学仿真模型模拟该工况,根据解算出的载荷优化悬置支架,最终解决支架断裂问题,得到如下结论。 (1)常用校核悬置支架强度的28种工况包含了车辆基本的使用工况,但一些整车误用工况未包含在内,在做悬置设计时,应根据车辆设计的使用工况,对校核工况进行一定调整。 (2)为得到某些工况下悬置的受力情况,可通过整车动力学仿真模型模拟分析实际工况,进而得到悬置的载荷。这个过程中要对整车动力学模型进行验证,以保证载荷解算的准确性。 (3)悬置支架优化作为典型的连续体结构优化,采用变密度法进行拓扑优化,可快速得到较理想的优化结果,优化后需进行相应的校核分析和试验验证。 [1] 吕振华,罗捷,范让林. 汽车动力总成悬置系统隔振设计分析方案[J].中国机械工程, 2003,14(3):265-269. [2] 黄庆,杜登辉,黄小飞.动力总成悬置支架的多工况拓扑优化[J].汽车技术,2008(10):27-30. [3] 俞雁,兰凤崇. 汽车发动机悬置支架断裂失效分析[J].冶金从刊,2012(1):25-29. [4] 谢涛,刘静,刘军考.结构拓扑优化综述[J].机械工程师,2006(8):22-25. [5] 刘旭红,欧笛声.基于SIMP优化理论的注塑机固定模板拓扑优化[J].中国塑料,2008,22(2):90-92. [6] 左孔天,陈立平,钟毅芳,等.基于人工材料的密度的新型拓扑优化理论和算法研究[J].机械工程学报,2004,40(12):31-37. [7] 周传月.工程有限元与优化分析应用实例教程[M].北京:科学出版社,2005. [8] 王明强,李志多.面向制造的连续体结构拓扑优化设计方法研究[J].中国机械工程,2010,21(5):524-528. [9] 上官文斌,蒋翠翠,潘孝勇.汽车悬架控制臂的拓扑优化与性能计算[J].汽车工程,2008,30(8):709-712. [10] 吕兆平,闫剑滔,李宏庚,等.基于有限元技术的动力总成悬置支架拓扑优化的研究[J].汽车工程,2009,31(4):321-325. A Research on Structure Optimization of Engine Mount Bracket Based on Misuse Working Condition Guo Shaoliang, Li Jinchao, Xiong Fei, Zhou Xinmei & Li Yufa AutomotiveEngineeringInstitute,GuangzhouAutomobileGroupCo.,Ltd.,Guangzhou511434 In the development process of a passenger car, its engine mount bracket was broken under a misuse working condition. According to a preliminary judgment by macroscopic fractography, the rapid break of mounting bracket is caused by overloading in misuse condition. Based on this, a vehicle dynamics model is built to simulate the misuse condition, with the load on the bracket obtained and a corresponding structural strength check conducted. The results reveal that the mounting bracket does not meet the strength requirements, and the bracket risky position by analysis is consistent with that really happened. Finally a topology optimization is performed on the bracket with both misuse condition and 28 conditions for strength check commonly used. A sample part of optimized scheme for the bracket is produced and installed on real vehicle for field test with no break happened again. The research provides important references for the strength design of engine mount bracket. engine mount bracket; vehicle dynamics; FEA; topology optimization 原稿收到日期为2016年7月4日,修改稿收到日期为2016年8月8日。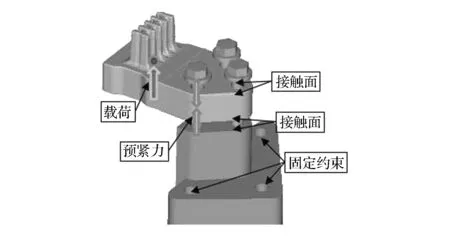

3 试验验证



4 结论

