承载式车身快速疲劳试验与CAE分析相关性的研究*
孙 涛,郑 非 ,刘 斌,郑松林
(1.上海理工大学机械工程学院汽车工程系,上海 200093;2.上汽集团商用车技术中心,上海 200438;3. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室,上海200093)
2016063
承载式车身快速疲劳试验与CAE分析相关性的研究*
孙 涛1,3,郑 非1,3,刘 斌2,郑松林1,3
(1.上海理工大学机械工程学院汽车工程系,上海 200093;2.上汽集团商用车技术中心,上海 200438;3. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室,上海200093)
本文中采用PAVE试验与疲劳寿命虚拟分析技术相结合的方法,对某承载式车身结构进行了疲劳寿命分析。根据结构疲劳寿命分析理论,采用有限元分析方法,对车身结构的疲劳寿命进行预测分析,同时在PAVE路面上进行快速试验。通过分析与试验结果的对比,验证了PAVE强化耐久试验与CAE分析的相关性,分析了造成车身结构若干区域寿命低的原因,并提出了改进方案,从而有效解决了该车车身疲劳寿命设计中存在的缺陷,为后续设计提供参考。
汽车工程;PAVE试验;有限元法;疲劳寿命;比利时路;强化系数
前言
承载式车身结构广泛应用于现代轿车与轻型商用车的车身结构中,与传统的车身-车架结构形式相比,承载式车身具有制造成本低,质量轻,整车质心高度低等优点,从而在一定程度上改善了汽车的操纵性能及燃油经济性。然而,该型车身的弯曲、扭转刚度和强度等指标的变化,以及由此可能产生的振动和噪声等乘坐舒适性指标的降低,将直接影响驾乘感受和整车使用寿命与性能品质。为此,承载式车身的可靠性问题必须在产品开发阶段加以重视。
常规的疲劳耐久试验需要耗时半年进行一轮试验,从而发现并解决问题,严重制约了新车开发进程,如果问题难以规避,重新设计与制造将使开发周期再次延长。与常规试验方式相比,PAVE 快速疲劳耐久性试验的周期大幅缩短到20天左右,并通过使用CAE,预测车身的疲劳性能。与PAVE试验结果进行相关性分析,可及时发现问题并提出改进方案,极大地缩短承载式车身耐久性开发周期。PAVE试验与CAE分析相结合的一体化开发流程如图1所示。

图1 一体化开发流程
文献[1]和文献[2]中针对车辆零部件疲劳耐久性进行了大量研究,积累了一整套从路面试验,理论分析到可靠性评价的研发流程和数据资料,并形成了成熟的规范体系。然而,相对于国外,国内对汽车结构疲劳寿命的研究工作起步较晚,研究的对象也大多限于主要零部件的疲劳寿命理论分析[3-4]。本文中着重研究某承载式车身快速疲劳试验与有限元法的相关性分析,从而提供解决设计开发初期车身疲劳寿命预测及试验等效性等问题的思路。
1 疲劳寿命指标下的强化系数数学模型
PAVE试验的路面是比利时路,俗称石块路,是汽车耐久性试验中最典型的路面之一[5]。由于沿道路纵向的随机数列都具有相同的自谱密度,而轮距相同的两车辙所对应的随机数列具有相同的互谱密度,从而保证了车辆在路面上行驶时的振动输出特性与行驶路线选择无关[6]。PAVE试验规范就是根据比利时路面强化系数制定的。
本文中研究的对象为某乘用车的商用汽车承载式车身,根据其在某试验场比利时路测得的载荷时间历程,通过双参数雨流计数法和Goodman疲劳经验公式进行零平均应力的应力循环等效转换,运用Basquin公式拟合得到零部件S-N曲线,然后经过三参数威布尔分布和程序载荷谱对数据进行处理,按照修正的Miner疲劳累积损伤理论得到频率因子与损伤因子,最后,求出比利时路面的强化系数,从而确定了该承载式车身在此试验道路行驶的强化系数。
1.1 载荷时间历程的统计
利用在某试验场进行的汽车车身载荷测试数据,经过对试验突变数据和高阶多项式趋势项的判断与消除后,运用双参数雨流计数法[7],可以得到车身载荷时间历程信号均值与幅值雨流矩阵直方图,如图2所示。
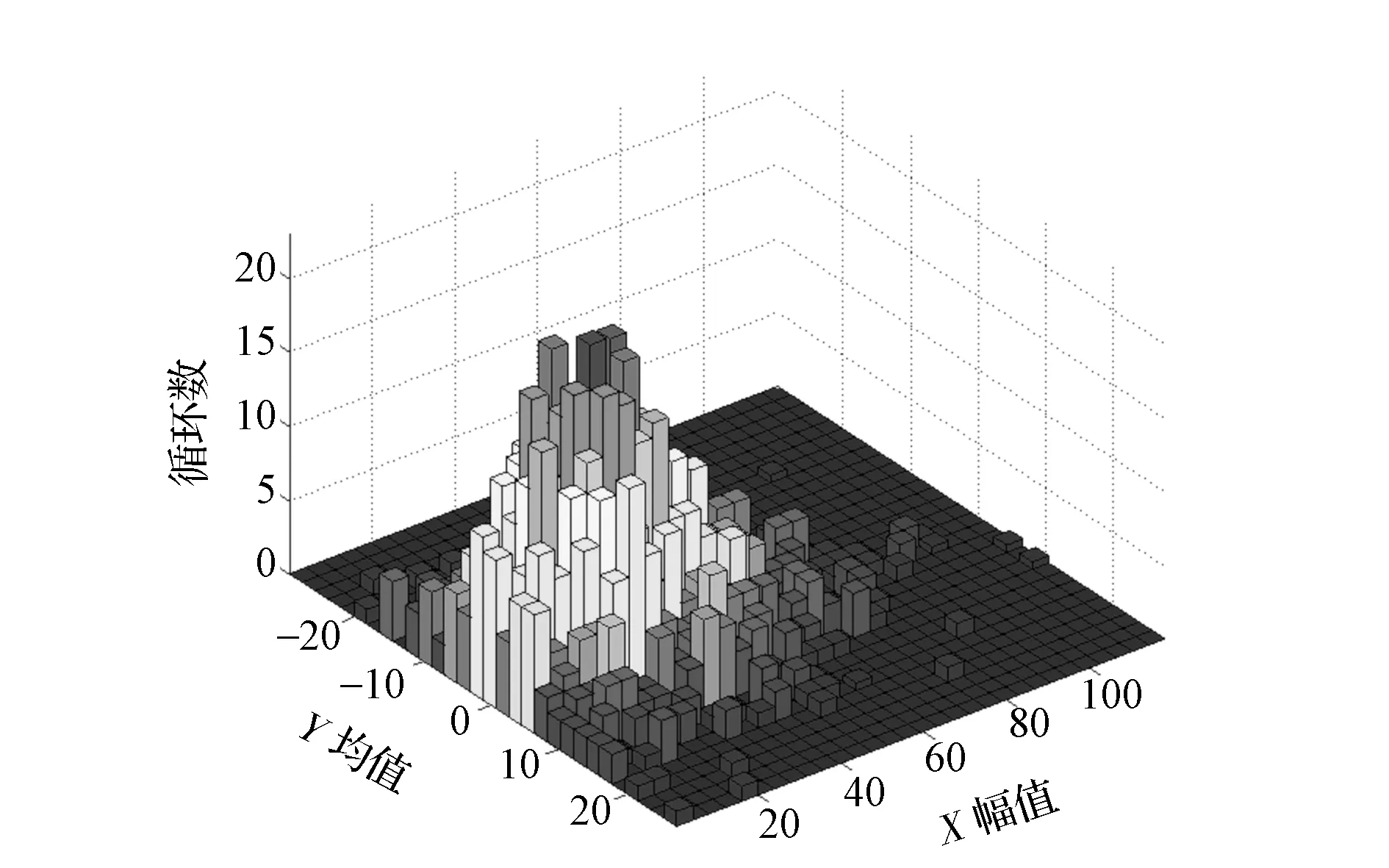
图2 雨流矩阵直方图
由于本文中采用修正的Miner疲劳累积损伤理论进行强化系数的计算,但Miner理论假定对称循环载荷加载,也就是载荷均值为零,而上述经雨流计数统计的均值不为零,因此,必须对试验数据中的非零平均应力的应力循环等效转换成零平均应力的应力循环。为此,应用Goodman线性经验公式进行等效转换,即
(1)
式中:σai为第i次循环应力幅值;σi为第i次循环等效零均值应力;σmi为第i次循环平均应力;σb为拉伸强度极限。
1.2 材料和零部件的疲劳性能曲线
在工程运用上,由于Basquin公式形式简单,计算方便且对数据的拟合度高,所以,多用来对材料疲劳性能进行拟合进而得到零部件的疲劳性能曲线,其公式为[8]
(2)
式中:σa为应力幅值;N为对应的疲劳寿命;M和C为与材料及试样的加载有关的常数。
而零部件的疲劳性能不仅要考虑材料的疲劳性能,还要考虑尺寸、表面加工和应力集中,即
(3)

对Basquin公式两边取对数得到一个线性疲劳性能拟合公式,再根据文献[9]可推出本文中所用材料SAPH400的BasquinS-N曲线方程为
lgN=-6.67lgσ+20.41
1.3 等效应力幅值分布函数的估算及其检验
在疲劳强度可靠性设计中,表达疲劳强度分布的函数除了正态分布函数外,还有威布尔分布概率密度函数。由于威布尔分布概率密度函数存在最小寿命,即100%存活率的寿命,是符合疲劳破坏实际情况的,故采用三参数威布尔分布,其概率分布函数为
(4)式中:w为形状参数;η为尺度参数;γ为位置参数。
相应的分布参数利用MATLAB进行估计,得到:w=1.1413,η=26.2255,γ=12.7009。在威布尔概率纸上绘出比利时路等效应力幅值及其概率和拟合直线,如图3所示。
根据威布尔函数可以转化成直线关系[10],利用这种关系可以检验试验数据是否符合威布尔分布。在图3绘制的威布尔分布概率纸上,不加位置参数的双参数威布尔分布数据的拟合曲线是一条近似直线的曲线;而加了位置参数的三参数威布尔分布数据的拟合曲线基本上是一条直线,更符合威布尔分布。

图3 威布尔分布概率纸
对于上面根据Goodman公式等效转换得到的数据,通过对其进行K-S检验[11],确定等效应力幅值均服从三参数威布尔分布。
1.4 程序载荷谱的编制
由于试验条件和有限载荷数据采集量等因素的限制,采集到的数据基本上是正常载荷,很少有大载荷出现,但影响疲劳寿命的重要因素之一就是少数极值载荷,不考虑极值载荷的估计结果会造成很大误差,所以,需要由实测载荷扩展出极值载荷。根据工程经验一般取10E6的累积循环过程中出现最大应力幅。因此,采用10E-6超值累积频率的概率分布公式即可求得最大应力幅值。
(5)
式中:K(x)为实测载荷样本的分布函数;Smax为极值载荷。
于是,可以得到极值应力幅值σmax=250.6MPa。运用Conover理论[12]将实测载荷谱分为8级程序载荷谱,以便进行强化系数的计算。
1.5 疲劳累积损伤理论及强化系数的计算
疲劳累积损伤理论认为,当材料承受高应力时,每一循环都使材料产生一定量的损伤,当损伤积累到临界值时发生破坏,这也就是材料固有寿命的消耗过程。由于Miner线性疲劳累积损伤理论[13]表达式简单,所以被广泛应用到疲劳寿命预测中。总损伤量D为
(6)
式中:di为构件在ni次循环所受的损伤;Ni为S-N曲线上对应于等效应力幅值σi的破坏循环次数。根据Miner提出的假设,当D=1时零件累积损伤结束,即发生疲劳失效。根据Basquin疲劳特性曲线公式,可得
(7)

根据程序载荷谱:
(8)
式中:nL为各级载荷的总循环数;θi为第i级应力幅水平下的频次率;αi为程序载荷谱中对应于第i级等效应力幅值的循环数。将式(7)中的Ni代入式(6),再将式(8)代入式(6)中,并认为D=1时发生疲劳失效,得到关系式为
(9)
由于用里程数表示寿命会更加直观,所以用L2(普通路面上车身发生疲劳失效时所行驶的路程)除以L1(比利时路面上车身发生疲劳失效时所行驶的路程)得到强化系数为
(10)
根据里程数与应力循环数成正比的关系,将式(9)中nL换算成总里程数L,得
(11)
式中:v0和t0为L0里程数对应的速度和时间。
令
(12)
(13)
则得
(14)
式中:F1和F2分别为比利时路面和普通路面的频率因子统计量;E1和E2分别为比利时路面和普通路面的损伤因子统计量。
根据以上建立的强化系数公式可以计算出白车身在比利时路面的累积损伤。但这样预测出的疲劳寿命精度还不够高,需要用Miner线性累积损伤理论进行修正。根据文献[14]中采用H.T.科尔顿和T.J.多兰提出的强度系数指数a代替Basquln关系式的m,a=(0.81-0.94)m,通常取a=0.85m。结合上述的 BasquinS-N曲线方程中的m,可得车身的强度系数指数a=5.6695。因此,根据以上数学模型和推导关系式可计算出路面强化系数,计算结果如表1所示。

表1 PAVE路面强化系数计算
由计算得到的强化系数可知,该车在比利时路面上行驶1km对车身造成的疲劳损伤等效于在B级路面上行驶11.5km所造成的疲劳损伤。
2 承载式车身PAVE耐久性试验方案
实车道路试验的地点在某试验场的比利时路面。试验道路和试验用车如图4所示。
依照《GB/T 12428—2005 客车装载质量计算方法》、《GB/T 12534—1990 汽车道路试验方法通则》和《 GB 15082—2008 汽车用车速表》等法规进行试验。PAVE路面整个循环实际里程为0.7km,其中有效试验里程为0.65km,总共进行2 600个循环。
试验时,车辆以40km/h的车速在PAVE路面上行驶,在连续完成PAVE路面试验一次计为一个循环。每天完成试验要求循环后,试验工程师需要记录当天行驶的试验里程数,记录车辆发生的故障和问题,填写试验报告。试验结束后,编写出试验车辆最终的评估报告。
3 试验结果分析、改进和试验验证
通过一轮PAVE试验,得到了相关5处主要疲劳失效位置,主要包括后悬架接触区域(吊耳和吊耳支架)、中门、尾门边框区域以及连接车体和车顶的D柱区域等,这与CAE仿真结果分析得到的主要问题区域基本一致。观察这些失效问题不外乎是由于结构几何尺寸不连续(如孔、切口等)造成应力集中,或是施加于零件上的载荷过大。对于第一种问题可以采用改变结构几何特征或局部加强的方法解决,第二种问题可以采用隔离载荷路径或局部加强的方法解决。表2列举了这5处主要区域在试验中出现的失效问题和CAE评估,验证了PAVE强化耐久试验与CAE评估的相关性,并给出了设计改进方案。
PAVE路试229循环后发现板簧前吊耳钣金开裂,如图5所示。

图5 吊耳钣金开裂
首先,分析板簧前吊耳开裂是否是由于生产制造过程所造成的,其中包括钣金的结构和厚度以及生产和装配过程是否符合设计要求,焊点位置的分布和焊接质量是否符合要求。如果没有上述问题,就要分析是由结构设计缺陷还是疲劳失效引起的。结构设计缺陷是因为几何结构设计失误导致应力集中,如某些地方未加加强筋、翻边等;而疲劳失效是受到比利时路面传来的激励源车身不断经受着周期性载荷,疲劳损伤累计到一定程度造成的。为此,先确定板簧前吊耳开裂区域的应力是否超过材料的屈服极限,如果经分析没有超过屈服极限,那就很可能是结构设计缺陷导致的问题,否则,就从疲劳失效方面找原因。从图5的照片分析看来,开裂位置在板簧吊耳与车身连接处,观察开裂状况是从R角外缘开始向内延伸的,通过有限元分析发现,在转向工况下开裂位置应力为517MPa,如图6所示,而在垂向bump工况下,开裂区域应力为495MPa,如图7所示,即已经远远超过其材料SAPH400的屈服极限240MPa。这是典型的由于路面不平度过大引起的轮胎动载荷传至车身板簧吊耳与车身连接处而产生的垂向剪切力所造成的疲劳失效。

表2 PAVE试验问题与CAE评估
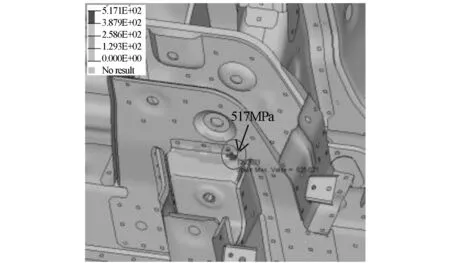
图6 转向工况分析
出于汽车产品研发时间和成本等因素的考虑,工程上通常采用改变钣金材料、增加三角筋、翻边、改变边缘倒角尺寸等增强局部刚度的方法来解决上述开裂问题。考虑到原结构前板簧吊耳与车身连接处,受到很大的冲击载荷,尤其是在吊耳折角区域,决定重点针对该部件的吊耳折角区域进行局部改进。图8为各个结构的局部改进方案。

图7 垂向工况CAE分析

图8 局部改进方案
图8中,方案一是延长开裂处钣金边界,方案二是在R角区域增加图示3处三角筋,并将钣金材质改为HC340LA(屈服极限为380MPa)。为了确保板簧前吊耳钣金不再开裂,将两个方案同时采用,调整后CAE分析结果如图9和图10所示,应力降低约25%。整车完成新一轮PAVE试验后,原开裂位置没有开裂,板簧前吊耳其他部位也没有出现新的开裂问题。

图9 转向工况改进

图10 垂向工况改进
另外,经过PAVE路试第893循环后,发现左右D柱附近焊点开裂,如图11所示。

图11 焊点开裂
对路试车左右D柱附近焊点区域进行查看,发现该处焊点所处位置为D柱骨架两层钣金之间的焊接点,焊点开裂形式是从根部开始出现裂纹,这说明在PAVE路面下侧围蒙皮结构产生较大变形,D柱失效焊点区域两个钣金件连接处存在较高剪切应力,经有限元疲劳分析(designlife),在常规车身扭转工况下,失效焊点寿命对数为3.9,如图12(a)所示,即最短寿命为7 943次循环,折合行程5 560km,与PAVE路试折合成常规道路的6 250km出现开裂的情况比较接近。焊点开裂风险高,故采用两种结构改进方案对比,方案一,取消失效焊点。区域焊点寿命(对数值)由3.9提升为4.7,如图12(b)所示,即最短寿命为50 118次循环,折合35 082km,焊点开裂风险低。但车身后端开口模态降低0.36Hz;扭转工况下尾门框开口变形增大3%。方案二,失效焊点保留,在该处加涂高强度结构胶。该区域焊点寿命对数提升到4.9,如图12(c)所示,即最短寿命为79 432次循环,折合55 602km,风险低于方案一。采取方案二进行新一轮PAVE路试,结果该处焊点再未开裂。

图12 CAE分析与改进
通过对以上5处疲劳失效区域的分析可以看出,PAVE强化耐久试验与CAE评估基本吻合,在车身开发初期可以帮助工程师快速准确地寻找到失效区域,并佐证了CAE的分析结果,很大程度上缩短了新车开发周期,降低了开发成本。
4 结论
本文中统计分析了某承载式车身载荷谱数据,并通过修正的Miner线性疲劳累积损伤理论求得该车身的疲劳寿命,计算得出了PAVE试验规范中的强化系数,然后对PAVE试验过程进行了分析,通过试验结果与仿真结果的关联分析,验证了PAVE强化耐久试验的有效性,为实施承载式车身快速疲劳验证和改进设计提供了理论和试验参考。
[1] HAIBA M, BARTON, D C, BROOKS P C. Review of Life Assessment Techniques Applied to Dynamically Loaded Automotive Components [J]. Computers and Structures, 2002, 80:481-494.
[2] VELLNICHAMY S. Transient Dynamic Fatigue Analysis of Automotive Structures Using Proving Ground Road Profiles[C]. SAE Paper 2005-01-0514.
[3] 高云凯,李翠,崔玲,等.燃料电池大客车车身疲劳寿命仿真分析[J].汽车工程,2010,32(1):7-12.
[4] 赵婷婷,李长波,王军杰,等. 基于有限元法的某微型货车车身疲劳寿命分析[J]. 汽车工程,2011,33(1):429-432.
[5] 王秉刚,等.海南汽车可靠性试验石块路的设计[J].汽车工程,1985,7(1):17-18.
[6] KIM Dongho , JOOS anggun . Generation of 3-D Virtual Block Belgian Road for Prediction of Road Load[C]. SAE Paper 2011-28-0077.
[7] 王宏伟.雨流计数法及其在疲劳寿命估算中的应用[J].矿山机械,2006,34(3):94-97.
[8] 高镇同,熊峻江.疲劳可靠性[M].北京:北京航空航天大学出版社,2000
[9] 石来德.机械的有限寿命设计与试验[M].上海:同济大学出版社,1990.
[10] 徐灏.疲劳强度设计[M].北京:机械工业出版社,1981.
[11] 闫仕军.汽车试验场道路强化系数的研究[D].吉林:吉林大学,2001.
[12] 樊晓燕, 童忠钫.机械零部件疲劳载荷谱编制[J].机电工程,1994(2):23-26.
[13] 徐灏.疲劳强度[M].北京:高等教育出版社,1988.
[14] 郭虎.汽车试验场可靠性强化试验强化系数的研究[D].杭州:浙江大学,2003
第八届国际汽车变速器及驱动技术研讨会即将在北京召开
由中国汽车工程学会和中汽翰思管理咨询公司联合举办的第八届国际汽车变速器及驱动技术研讨会(TMC 2016)将于今年4月28-29日在北京富力万丽酒店召开。研讨会将提供45场报告,介绍和讨论传统动力汽车变速器提升技术、(插电)混合动力变速器和电动汽车多挡变速器技术。
丰田汽车、采埃孚、麦格纳、格特拉克、AVL、IAV、邦奇动力、PUNCH Powerglide等公司将分别介绍最新的增程式、专用变速器DHT、P2、P3、P4等混动变速器和驱动技术解决方案及研发技术。
会议将邀请上汽集团高层领导介绍上汽在新能源汽车驱动技术的实践和战略,并将组织一场高层互动论坛,就市场需求、关键性能目标、技术方案、成本控制、生产规模、平台化和时间表进行更为深入的讨论。会议还将邀请上汽捷能、上海交大、清华大学和AVL介绍和讨论混合动力变速器的测试技术和标准问题。
博格华纳、贺尔碧格、Protean、hofer、里卡多、SMT等公司将在本届会议上分别介绍纯电动汽车多挡变速器及相关技术。本届研讨会将继续深入介绍和讨论最新的变速器、零部件技术、开发技术及分享开发技术实践经验。
A Study on the Correlation Between Accelerated Fatigue Test and CAEAnalysis for a Unitized Vehicle Body
Sun Tao1,3, Zheng Fei1,3, Liu Bin2& Zheng Songlin1,3
1.DepartmentofAutomotiveEngineering,SchoolofMechanicalEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai, 200093;2.SAICMotorCommercialVehicleTechnicalCenter,Shanghai, 200438; 3.MachineryIndustryKeyLaboratoryforMechanicalStrength&ReliabilityEvaluationofAutoChassisComponents,Shanghai200093
By combining PAVE test and virtual fatigue analysis technique, the fatigue life of the unitized body structure of a light commercial vehicle is analyzed in this paper. Based on the theory of structural fatigue life analysis, the fatigue life of the body structure is predicted by finite element analysis (FEA), and meanwhile a PAVE accelerated test is also conducted. By comparing the results of FEA and PAVE test, the correlation between CAE analysis and PAVE intensified durability test is validated, the causes of low fatigue life in several areas are analyzed with some improving schemes proposed, and hence the defects in the fatigue life design of the vehicle are effectively remedied, providing references for subsequent design.
automotive engineering; PAVE test; FEM; fatigue life; Belgian road; intensifying factor
*上海市科研创新项目(12ZZ145)资助。
原稿收到日期为2014年9月28日,修改稿收到日期为2015年2月3日。

