基于变压器马尔可夫状态评估模型和熵权模糊评价方法的风险评估技术研究

张 桦，魏本刚，李可军，梁永亮



基于变压器马尔可夫状态评估模型和熵权模糊评价方法的风险评估技术研究

张 桦1，魏本刚2，李可军3，梁永亮3

(1.重庆大学电气工程学院，重庆 400044；2.上海市电力公司电力科学研究院，上海 200437；3.山东大学电气工程学院，山东 济南250061)

为建立有效的电力变压器设备风险评估方法，针对变压器故障机理的复杂性和不确定性特征，提出了基于状态检修和马尔可夫过程的变压器全态状态评估模型。利用分指标研究变压器缺陷严重度，结合变压器分部位故障频率计算模型，采用熵权模糊计算量化变压器设备风险等级，构建设备风险评估矩阵，给出了一种新的变压器运行风险评估方法。仿真程序实例计算结果表明，所提方法能够准确计算变压器各组成部分的风险值，并获得针对性的维修策略，变压器风险评估结论是准确、有效的。

电力变压器；马尔可夫过程；熵权模糊综合评价；风险评估；维修策略；故障频率

0 引言

电力变压器是电力系统的关键设备，其运行可靠性直接关系到电力系统的安全稳定，风险评估作为直观方法可直接反映变压器运行的可靠性。近年来，电力设备状态检修工作在国家电网公司等电力企业逐步深化[1-7]，电力设备的风险评估工作也得到深入开展。以往的电力设备检修策略主要基于设备本体状态，未考虑设备对整个电力系统运行的影响因数以及经济性指标，加之变压器内部结构复杂，故障种类繁多、原因复杂，目前国内外状态检修体系没有建立基于综合指标的风险评估方法，亟待引入新的风险评估模型来指导变压器状态检修。

风险评估作为变压器风险维修的基础[8-12]，国内众多专家学者进行了研究工作，但并未将近年来新兴的变压器状态检修策略引入模型。同时，众多学者在风险评估和状态检修技术的研究过程中应用了模糊综合评判或马尔可夫过程理论[12-14]，但研究方法相对较单一，还未有将两种方法进行综合应用的成功实践。本文建立基于马尔可夫过程、熵权模糊综合评价和状态检修技术的变压器风险评估策略，解决了单一方法下设备状态无法进行整体评价、检修策略针对性不强等问题，实现了变压器类设备状态评价理论模型的实用化，可对一段时间内某地区变压器分部位运行状况的风险评估。实际案例证明，该方法是准确、有效的，为制订、优化设备检修计划提供了科学依据，为考虑变压器历史数据和经济效益的风险评估提供了新的思路。

1  基于状态检修的变压器马尔可夫状态评估模型

1.1 修正后的变压器马尔可夫状态评估模型

马尔可夫过程是基于概率统计的特殊的随机过程，能够很好地描述可修复系统投入使用后处于某种状态的概率，并分析出系统可靠性。系统由一种状态转移到另一种状态的概率与系统早先的历史无关，即无记忆性，就可以运用马尔可夫过程来分析该系统的可靠性[15]。

根据国家电网公司颁布的《输变电设备状态检修导则》[16]，综合考虑实际运行中变压器可能出现的故障形态，可建立融合状态检修策略的变压器全态模型，如图1所示。

图1 变压器全态模型

该模型描述了变压器在运行过程中可能出现的全部状态。其中其他故障原因，主要是指除以上几种故障以外的故障，如人为误操作、自然灾害等。变电站施工或改造等因素发生的概率极低，所以此处暂不考虑。

变压器的运行状态视为是可修复的，其状态转移问题可由马尔科夫过程来解决。由变压器全状态模型，按照文献[15]对故障率和修复率的定义，分别把不同状态的故障率和修复率用和表示。根据文献[17]，结合状态检修技术进行修正后，变压器运行状态的马尔科夫状态转移图如图2所示。

1.2 分部位故障频率计算

电力系统中常用频率法和持续时间进行可靠性分析。频率法，是指以频率的方式表示系统出现某种状态的概率，即期望次数。比如，假设变压器处于某状态的频率为f，则f为其在单位时间内停留在此状态的期望(期间可由其他状态转入，也可由此状态转出)，有：

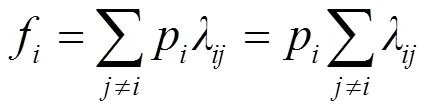
式中，λ为状态转移率，指从状态向状态转移的期望次数。至此，便可由变压器的历史运行数据得到变压器的故障率和修复率，并最终得出变压器各部位的故障频率f,f(1,2,3,…,7)分别代表铁芯、绕组、套管、冷却系统、分接头装置、绝缘介质、其他这7个部位的故障频率。

2  变压器缺陷的评价方法

2.1 缺陷评价方法的选择

模糊评价方法是在考虑多种指标的影响下，运用模糊数学工具对指标所描述事物作出综合评价的方法[18]。采用熵权作权重，充分利用已知数据信息，很大程度上避免了常权作权重的主观性和不合理性。同时，各评价指标的权重应为指标客观信息与专家评价主观信息的综合，更真实、合理地反映各指标的实际权重。因此本文将熵权模糊综合评价方法应用到缺陷的评价当中。

2.2 确定缺陷影响的评价指标集和评语集

以往对变压器缺陷严重度的判定多基于常规的物理指标，本文从故障对生产生活造成影响的角度探讨严重度划分。结合实际经验，将缺陷严重度评价指标划分为直接损失、间接损失、检修费用、检修时间、监测水平共5个指标。

其中直接损失为可见、可统计的经济损失，以元为单位；间接损失为带给人们生产生活的间接损失，以元为单位；检修费用为相关部门检测维修费用，以元为单位；检修时间为从故障发生到修复所用时间，以小时为单位；监测水平指故障得到监测的难易程度，以100分为满分，分值越低表示越易于监测。以上5项指标均由所统计时间段内该地区电网企业或供电单位根据本地区实际生产生活情况，由相关专家衡量及打分给出具体值。其中间接损失项由于难于统计，本文将不予考虑。

设定变压器某部位缺陷的评价指标集1,2,3,4={直接损失，检修费用，检修时间，监测水平}。评语集为={1,2,3,4,5}=｛轻度，一般，比较严重，严重，特别严重｝，评语集中各值表示该部位故障对该评语的隶属度。

2.3 评价矩阵标准化

由评价指标集可得个评价部位的评价矩阵

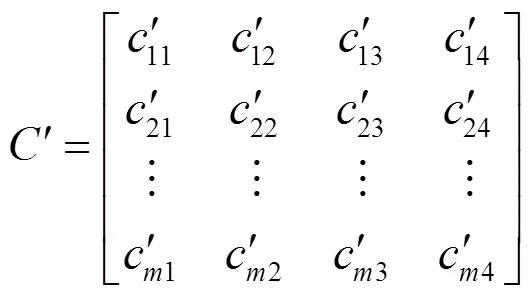
(3)

式中，c(1,2,…,;=1,2,3,4)为标准化评价指标，从而得到标准化评价矩阵

2.4 确定评价指标的熵权权重向量

由标准化矩阵可计算其第个评价指标的熵和熵权，其算式分别见式(4)和式(5)。

式中：H为第个评价指标的熵；f为变压器状态频率；；，并规定当f=0时，flnf=0。

(5)

式中：ω为第个评价指标的熵权，；。经计算便可得到4个评价指标的熵权权重向量为。

2.5 确定评价指标的综合权重向量

其中：为第个指标的综合权重；为第个指标的熵权权重；为第个指标的主观权重；为综合系数，且。

2.6 计算模糊评价矩阵

第个部位缺陷严重度标准化后的评价指标集为C={c1,c2,c3,c4}，即标准化评价矩阵的第行。其第个指标在评价集上的模糊子集可由其对的隶属函数来确定，本文隶属度函数取等腰三角形函数：

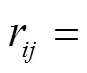
式中：r(v)为第个部位缺陷严重度的第个评价指标对评语v的隶属度；m,n,l为对应于评语v的常数。对等腰三角形隶属度函数做如下取值：1=0,2=0.25,3=0.5,4=0.75,5=1；取等腰三角形底边长为1.6，从而每个指标可取到4个评语的隶属度。从而得以下5个隶属度函数：

(8)

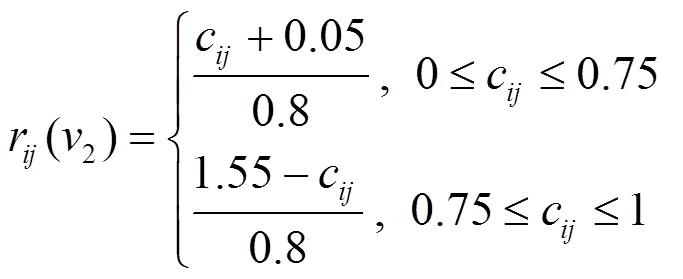
(10)

(11)

由此可得第个部位缺陷严重度的模糊评价矩阵为

2.7 求取终评模糊子集并确定缺陷严重度

终评评价子集为上的模糊子集，其算式为

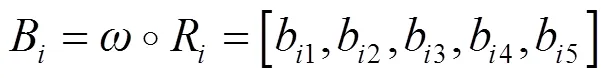
(14)

对进行归一化处理，算式为

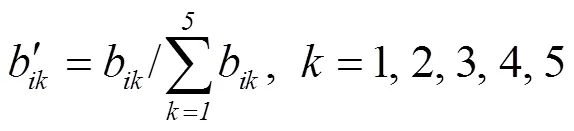
可得到第个部位缺陷严重度的模糊综合评价结果

(16)

3  变压器风险评估体系

由本文第1部分计算可得变压器各部位故障频率，将变压器故障频度分为4个等级，将变压器缺陷严重度分为5个等级，分别如表1、表2所示。

表1 故障频度等级

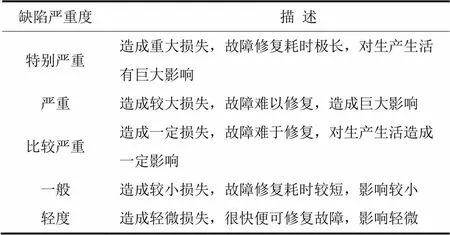
表2 缺陷严重度等级

风险的大小是对可能性和影响两个方面的综合度量，其值是事件发生可能性及影响两者的综合函数，对应于不同风险发生的可能性和影响，将产生不同的风险值。风险评估可以突出发生概率小但后果严重的事件，并将设备自身和系统损失结合起来[20]。为简化评估工作量，常采用二维平面矩阵进行风险评估，风险评估矩阵的横坐标是失效后果，纵坐标是失效可能性。失效可能性和失效后果的不同组合得到不同的风险等级。本文由已建立的评估体系，构造4×5风险评估矩阵，如表3所示，实现对变压器各部位的总体风险评估。其中，风险评估矩阵中各风险值定义如表4所示。

表3 变压器部位风险评估矩阵

Table 3 Risk assessment matrix for part of transformer

表4 风险值定义

Table 4 Definition of risk values

4  算例分析

本文采用文献[15]中给出的某地区1999-2002年220 kV变压器计划停运和非计划停运按部位分类的平均故障率和修复率数据，进行算例的计算分析。数据如表5-表7所示。

由式(1)可求出变压器11种状态的全态概率P(=0, 1, 2, …, 10)，由式(2)可计算变压器8种状态的频率f(=0, 1, 2, …, 10)，结果如表8所示。

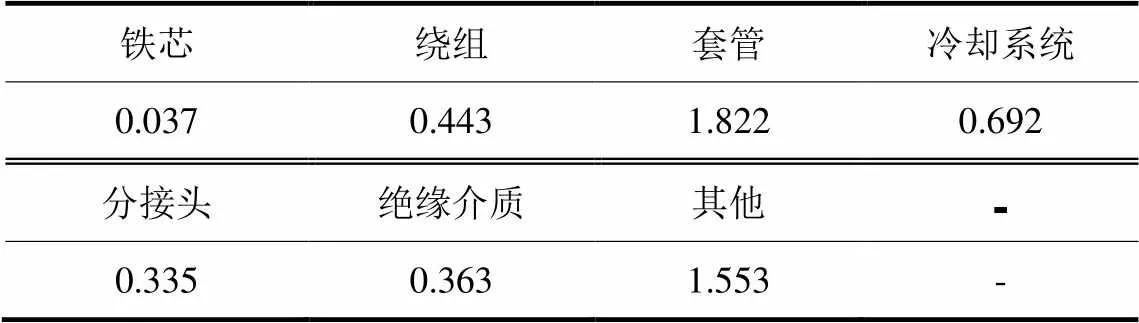
表5 变压器非计划停运故障率

表6 变压器修复率

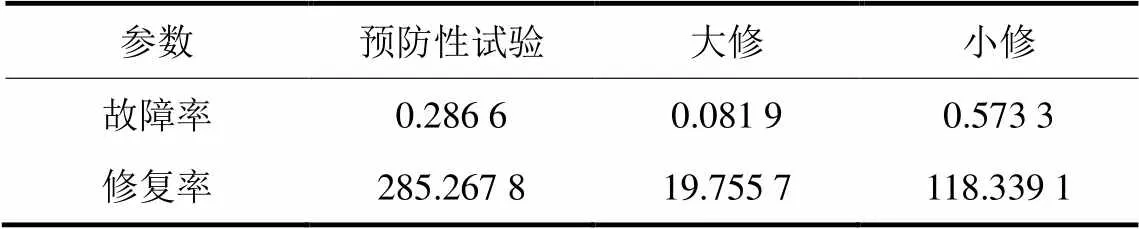
表7 计划停运的故障率和修复率

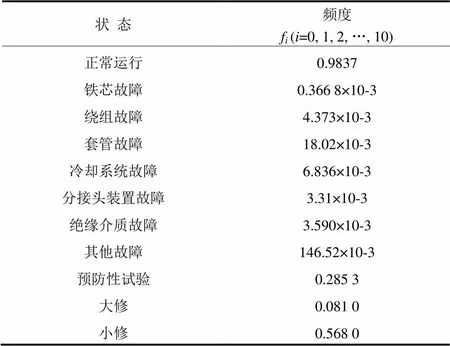
表8 变压器全态频率

由表9可得到变压器7个部位、缺陷严重度4项评价指标的评价矩阵；依次由式(3)进行评价矩阵标准化得标准化矩阵；由式(4)、式(5)计算熵权权重向量；假设专家主观权重向量为，取，由式(6)计算指标综合权重向量；由式(8)~式(12)计算第个部位缺陷严重度的模糊评价矩阵；由式(13)计算模糊子集，最后由式(14)归一化处理求得第个部位缺陷严重度的模糊综合评价结果，并由最大隶属度原则，选取中最大隶属度所对应的评语作为部位缺陷严重度的最终评语。

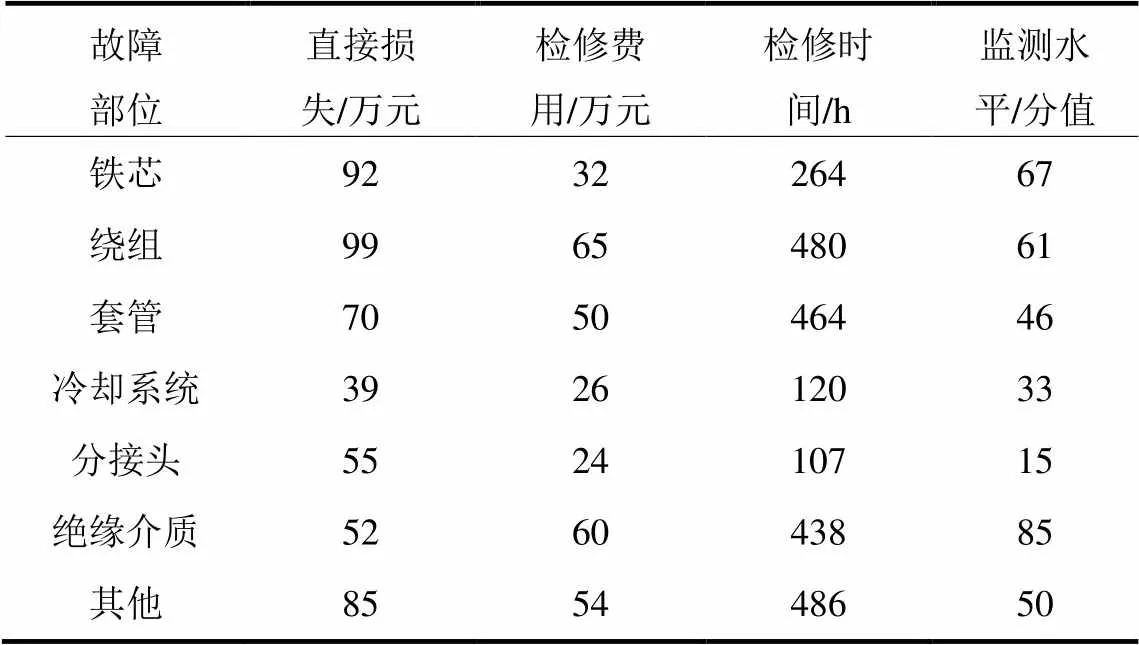
表9 变压器分部位缺陷严重度评价表

绕组、冷却系统、绝缘介质、分接头部位的风险亦为，其他部位风险值为，即面临中等风险，应优化维修策略，密切关注该部位健康状况。

分析可知，铁芯与套管的评估结论同为，但前者缺陷严重度为一般，重于套管，故同等情况下仍可优先考虑；其他部位故障频度评语为可能、缺陷严重度评语为比较严重，使其风险值达到，由于其他部位包含范围较多，非前6类故障均划归为其他故障，使其故障频率值较高。由以上风险评估结果，可知该地区变压器各部位总体健康状况较好，风险低，同时建议供电维修部门应密切关注其他部位健康状况，可优先开展对这些部位的普查维修。

5  结语

本文提出了基于马尔可夫过程和熵权模糊综合评价的变压器风险评估策略，建立了变压器全态模型，提出了对电力变压器所面临风险进行评估的方法步骤。通过算例的计算分析，证明该策略针对变压器类设备复杂的设备组附件及多评价因子的情况下，在对设备进行准确的状态评价及制定对应的检修策略方面是合理有效。相比现有通常方法，可有效提高设备状态评价水平和效率，并可分析变压器风险值，提出对应的检修策略，为变压器的风险评估提供了一种新的方法。

与现有的对单台变压器的状态评估方法不同，本文方法应用大量变压器历史数据，对设备的评价更为准确，同时可根据设备一定时期内的缺陷及故障特性，实现对某类重点关注设备的个性化分析，方法更加灵活有效，对不同运行特征的设备更有针对性。可实现某地区一段时间内多台变压器的分部位总体风险评估，提高设备状态评价的效率，为供电部门宏观范围上分部位的检修策略的制订、优化提供依据。

[1] 黄炜昭, 皇甫学真, 陈建福, 等. 电网主设备运行维护策略辅助决策方法[J]. 电力系统自动化, 2013, 37(10): 119-123.

HUANG Weizhao, HUANGFU Xuezhen, CHEN Jianfu, et al. An assistant decision-making method for operation and maintenance strategy of primary equipment in power grid[J]. Automation of Electric Power Systems, 2013, 37(10): 119-123.

[2] 汲国强, 吴文传, 张伯明, 等. 一种适用于状态检修的电力设备时变停运模型[J]. 中国电机工程学报, 2013, 33(25): 139-146.

JI Guoqiang, WU Wenchuan, ZHANG Boming, et al. A time-varying component outage model for power system condition-based maintenance[J]. Proceedings of the CSEE, 2013, 33(25): 139-146.

[3] 王献林, 吕飞鹏. 继电保护可靠性及其状态检修方法[J]. 电力系统及其自动化学报, 2014, 26(9): 65-70.

WANG Xianlin, LÜ Feipeng. Relay protection reliability and its state overhaul method[J]. Proceedings of the CSU-EPSA, 2014, 26(9): 65-70.

[4] 董雷, 张昭, 蒲天骄, 等. 基于PMU量测信息的电压稳定在线评估指标[J]. 电力系统保护与控制, 2015, 43(11): 1-6.

DONG Lei, ZHANG Zhao, PU Tianjiao, et al. An online voltage stability index based on measuring information of phasor measurement unit[J]. Power System Protection and Control, 2015, 43(11): 1-6.

[5] 马丽叶, 贾彬, 卢志刚, 等. 基于静态安全性和实时供电能力的输电网安全等级研究[J]. 电工技术学报, 2014, 29(6): 229-237.

MA Liye, JIA Bin, LU Zhigang, et al. Research on Security classification of transmission network considering static security and real-time power supply Capability[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 229-237.

[6] 王璟儒, 李川, 肖定垚, 等. 考虑风险度量与成本最优的电网资产全寿命周期管理问题[J]. 电网与清洁能源, 2014, 30(11): 26-31.

WANG Jingru, LI Chuan, XIAO Dingyao, et al. Whole life-cycle management of grid assets considering risk measurement and LCC optimization[J]. Power System and Clean Energy, 2014, 30(11): 26-31.

[7] 张镱议, 廖瑞金, 杨丽君, 等. 综合考虑可靠性与经济性的电力变压器检修方案优选[J]. 电工技术学报, 2014, 29(11): 191-200.

ZHANG Yiyi, LIAO Ruijin, YANG Lijun, et al. Maintenance decision making of power transformer by integrated considering reliability and economy[J]. Transactions of China Electrotechnical Society, 2014, 29(11): 191-200.

[8] 庞尔军, 唐贵基, 于虹, 等. 变压器信任度与安全指数的对比研究[J]. 电力系统保护与控制, 2014, 42(2): 139-145.

PANG Erjun, TANG Guiji, YU Hong, et al. A comparative study between the transformer trust degree and the security index[J]. Power System Protection and Control, 2014, 42(2): 139-145.

[9] 余文辉, 王沾, 曾祥君, 等. 基于贝叶斯网络的多状态变压器可靠性跟踪分析[J]. 电力系统保护与控制, 2015, 43(6): 78-85.

YU Wenhui, WANG Zhan, ZENG Xiangjun, et al. Reliability tracing analysis for multi-state power transformers using Bayesian network[J]. Power System Protection and Control, 2015, 43(6): 78-85.

[10]薛浩然, 张珂珩, 李斌, 等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制, 2015, 43(8): 8-13.

XUE Haoran, ZHANG Keheng, LI Bin, et al. Fault diagnosis of transformer based on the cuckoo search and support vector machine[J]. Power System Protection and Control, 2015, 43(8): 8-13.

[11]杨丽君, 齐超亮, 吕彦冬, 等. 变压器油纸绝缘状态的频域介电谱特征参量及评估方法[J]. 电工技术学报, 2015, 30(1): 212-219.

YANG Lijun, QI Chaoliang, LÜ Yandong, et al. Characteristic parameters and assessment methods of frequency-domain dielectric spectroscopy of oil-paper insulation for transformers[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 212-219.

[12]彭积城, 蔡金锭. 变压器油纸绝缘老化状态的探讨[J]. 高压电器, 2015, 51(5): 132-138.

PENG Jicheng, CAI Jinding. Discussion on evaluation of aging condition for transformer oil-paper insulation[J]. High Voltage Apparatus, 2015, 51(5): 132-138.

[13]赵云峰, 张永强, 聂德鑫, 等. 基于模糊和证据理论的变压器本体绝缘状态评估方法[J]. 电力系统保护与控制, 2014, 42(23): 57-62.

ZHAO Yunfeng, ZHANG Yongqiang, NIE Dexin, et al. Application of fuzzy and evidence theory in power transformers condition assessment[J]. Power System Protection and Control, 2014, 42(23): 57-62.

[14]PILLAY A, WANG J. Modified failure mode and effect analysis using approximate reasoning[J]. Reliability Engineering and System Safety, 2003, 79: 69-85.

[15] 郭永基. 可靠性工程[M]. 北京: 清华大学出版社, 2002.

[16]国家电网公司. Q/GDW 170油浸式变压器(电抗器)状态检修导[S]. 北京: 国家电网公司, 2008.

State Grid Corporation of China. Q/GDW 170-2008 guide for condition based maintenance strategy of oil-immersed power transformers (reactors)[S]. Beijing: State Grid Corporation of China, 2008.

[17]廖瑞金, 肖中男, 巩晶, 等. 应用马尔科夫模型评估电力变压器可靠性[J]. 高电压技术, 2010, 36(2): 322-327.

LIAO Ruijin, XIAO Zhongnan, GONG Jing, et al. Markov model for reliability assessment of power transformers[J]. High Voltage Engineering, 2010, 36(2): 322-327.

[18]顾煜炯, 董玉亮, 杨昆. 基于模糊评判和RCM分析的发电设备状态综合评价[J]. 中国电机工程学报, 2004, 24(6): 189-194.

GU Yujiong, DONG Yuliang, YANG Kun. Synthetic evaluation on conditions of equipment in power plant based on fuzzy judgment and RCM analysis[J]. Proceedingsof the CSEE, 2004, 24(6): 189-194.

[19]程崯, 王宇, 余轩, 等. 电力变压器运行状态综合评判指标的权重确定[J]. 中国电力, 2011, 44(4): 26-30.

CHENG Yin, WANG Yu, YU Xuan, et al. Study on index weighting methods for transformer condition evaluation[J].Electric Power, 2011, 44(4): 26-30.

[20]胡文平, 于腾凯, 巫伟南. 一种基于云预测模型的电网综合风险评估方法[J]. 电力系统保护与控制, 2015, 43(5): 35-42.

HU Wenping, YU Tengkai, WU Weinan. A comprehensive power grid risk assessment method based on cloud prediction model[J]. Power System Protection and Control, 2015, 43(5): 35-42.

Research on risk assessment technology based on Markov state evaluation model for power transformer and entropy-weighted fuzzy comprehensive evaluation

ZHANG Hua1, WEI Bengang2, LI Kejun3, LIANG Yongliang3

(1. School of Electrical Engineering, Chongqing University, Chongqing 400044, China; 2. Electric Power Technical Research Institute, SMEPC, Shanghai 200437, China; 3. School of Electric Engineering, Shandong University, Jinan250061, China)

To build an effective assessment method for the risk of electric power transformers, the full condition model of transformer based on condition-based maintenance (CBM) and Markov Process is established, considering the complexity and uncertainty of transformer fault. The research method of classified index is used for confirming the severity of transformer defects. Combined with the calculation model for subcomponent fault frequency, entropy-weighted fuzzy method is adopted to quantify the serious degree. Based on the above research the assessment matrix is established. Then a new assessment method for the risk of electric power transformers is given. The simulation program is compiled, and a case is analyzed by the risk assessment technology. The calculation result concludes the risk value and maintenance strategy. Empirical results show that the approach proposed is available and effective.

power transformer; Markov Process; entropy-weighted fuzzy comprehensive evaluation; risk assessment; maintenance strategy; fault frequency

10.7667/PSPC151240

2015-07-17；

2015-09-24

张 桦(1978-)，男，博士生在读，高级工程师,研究方向为电力系统可靠性、电网运行与分析；E-mail: jntony @163.com 魏本刚(1981-)，男，博士，高级工程师，研究方向为电力变压器试验及状态检修技术；E-mail: wbgsj@126.com 李可军(1972-)，男，博士，副教授，研究方向为输变电设备状态检修。E-mail: lkjun@sdu.edu.cn