计及输电介数及功率介数的电网待恢复区域重要性评估

陈碧云，叶仁欢，白晓清



计及输电介数及功率介数的电网待恢复区域重要性评估

陈碧云，叶仁欢，白晓清

(广西电力系统最优化与节能技术重点实验室(广西大学)，广西 南宁 530004)

电力系统因自然灾害引发大规模故障时，对电网待恢复区域进行重要性评估对于电网恢复策略的制定具有重要意义。针对已有评估模型中介数指标的不足，将复杂网络的共性与电网络的电气特性相结合，综合考虑线路介数和输电线路的最大输电能力，提出了输电介数的概念，并以输电介数作为电网络边权重求解节点网络凝聚度。最后结合各待恢复区域内发电机和负荷的功率特性，用节点功率介数对节点网络凝聚度指标进行修正，得出评估待恢复区域的重要性指标，从而确定了待恢复区域的物资需求优先级，给电力应急体系的物资调度提供参考。最后，以IEEE标准系统为例进行仿真分析，验证了所提方法的可行性和适用性。

待恢复区域重要性；网络凝聚度；输电介数；节点功率介数

0 引言

近年来，国内外频发的自然灾害给电网安全稳定运行和社会发展造成了严重的危害[1-5]。例如，2008年1月在冰灾的侵袭下，我国的电网损失惨重，其中国家电网停电用户总计2 705.78万户，电站停运884座，输电线路累计停运15 284条，配电线路累计受损15.26万km，电网因设施损坏而造成的直接经济损失高达104.5亿元。南方电网涉及54 046个工业用户、642.9万居民用户遭受停电，7 541条输电线路和859 座变电站停运，损毁线路杆塔126 247基，最终损失售电量超过72亿kW•h。2008年12月29日，美国大部分地区遭受暴风雨的侵袭，许多供电线路遭受损坏，数十万用户电力被中断。2014年7月，台风“威马逊”共造成广东、广西、海南的电力系统造成了严重破坏，三省的直接经济损失约295亿元人民币。

稳定的电力供应是维持社会秩序正常运转的重要因素之一，更是抗灾救灾的前提条件。及时恢复灾区重要负荷的供电对灾后救援、灾区重建和生产恢复都有十分重要的意义。因此，自然灾害发生时，有效的应急管理可以将灾害的规模、灾害损失控制在最低水平。由于每个受灾点的重要程度各不相同，在实施应急措施之前，需要对受灾点的重要程度做出合理的评估，从而制定及时有效的电网恢复策略。

目前，对于灾后电网恢复策略的研究，国内外学者对输电线路脆弱度的关注比较多[6-8]，而对电网待恢复区域重要性评估的研究较少。文献[9-11]基于复杂网络理论, 从电网拓扑结构出发，通过复杂网络理论的各拓扑特征参数描述电网节点的脆弱程度。文献[12]在文献[9]的电网无权网络拓扑结构基础上，引入线路阻抗值作为边权，求解了带有边权重的电网络节点重要度评估指标。文献[13]以线路最大传输容量为权重和熵度，提出节点的熵度指标来衡量节点的连通强度及连通强度的分布，并用于识别重要节点。文献[14]基于网络最大流和复杂网络理论，以电源点与负荷节点间的最大传输容量流经节点的功率作为节点介数来评估节点的重要性。文献[15]用连续潮流法求取线路最大输电能力，并以线路最大输电能力作为物资需求点重要性的唯一指标进行重要性评估。文献[16]用模糊层次分析法评估待恢复区域负荷的重要性，但评估待恢复区域的负荷重要性时只考虑了负荷而忽略了其他电气设备。文献[17]基于搜索矢量拟态物理学算法，对微电网的脆弱性开展了评估。文献[18]利用暂态能量函数混合法评估了电力系统的脆弱性。文献[19]根据功率在点网络中的流通关系，以线路介数和节点介数来评估线路和节点的重要性。文献[20]基于电网运行状态、网络拓扑结构，综合继电保护、节点电压等因素，提出了评估电网脆弱线路脆弱性的综合介数方法。文献[21]结合自定义的电网影响因子和聚合系数指标，评估了电力通信网中拓扑节点的重要性。

以上模型或方法大多仅从输电线路或负荷的某一方面进行电网络节点重要性评估，不能全面反映电网络节点的电气特性。本文在复杂网络理论的基础上，综合考虑线路介数、输电线路的最大输电能力和节点功率介数，提出了修正的节点网络凝聚度作为电网待恢复区域重要性评估指标，用于确定待恢复区的优先级。

1  电网待恢复区域的重要性指标

在网络拓扑结构中，将发电机、负荷和变电站看作节点，输电线路与变压器支路看作节点间的边。将节点与其相连的各条输电线路的1/2范围划为一个网络节点，视作电网待恢复区域[22]。如图1所示，虚线包含的区域a、b、c即为电网待恢复区域。

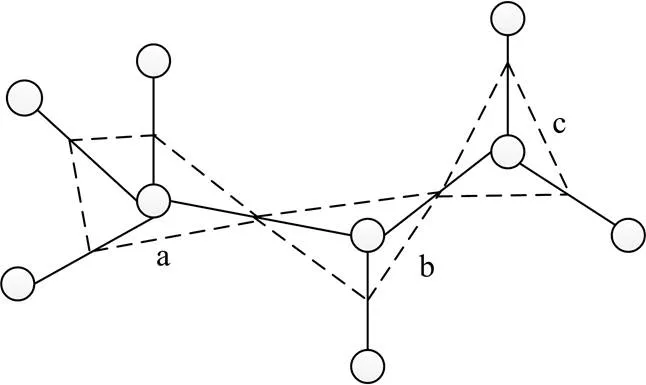
图1 电网待恢复区域示意图

1.1 带权重的节点网络凝聚度指标

用于衡量复杂网络中节点重要程度的常用指标有平均长度、节点度数、节点介数、节点介数累积分布、线路介数、线路介数累积分布、网络冗余性等。但以上指标在用于衡量电网络的节点重要程度时忽略了电网的物理性质，存在局限性[7]。而带权网络能够描述节点之间连接性的强弱，较全面地描述了复杂电网络的物理特性。因此，本文首先将电网络的边赋予权值，再将节点收缩后的网络凝聚度作为电力网络节点的重要度指标。

图2 节点收缩示意图

图2是节点收缩的示意图[9]。将图2(a)中与节点9相连的节点8、10、11与节点9短接，形成图2(b)中的新节点，并将原图中与8、10、11节点相连的节点连接到新节点上。待收缩节点将与其连接的节点收缩凝聚成新节点，收缩后的节点可将整个网络更好地凝聚在一起。节点收缩后的网络凝聚度为

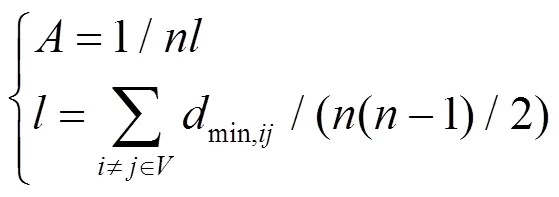
式中：为网络节点数；为节点的平均最短距离；为网络中任意两点与的最短距离，一般用边的数目表示，即认为边的权重为1，但是，这种表示方法无法体现电气距离[12]。复杂网络理论[23-24]中，常用线路介数来描述线路的重要程度，因此，本文定义线路的输电介数为节点间的边权重，即

(2)

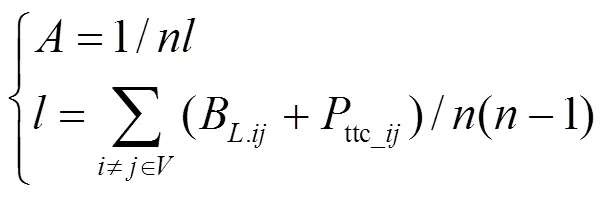
1.2待恢复区域的重要性指标

电网络节点的重要性除了考虑节点网络拓扑的重要性及其关联线路的重要性外，还应考虑节点内发电机和负荷的特殊性。因此，参考文献[21]的方法，借助介电系数的概念，引入节点功率介数如式(4)。

由式(5)、式(6)可定义节点的功率传输权重为

(7)

由于各个指标的数量级不统一，将各指标进行归一化处理可以避免数据对结果影响程度产生较大的误差。

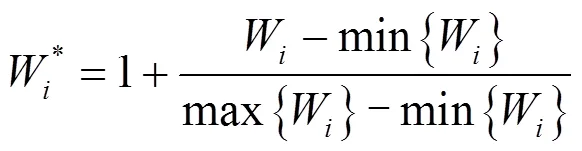
(2)的归一化计算公式为

(9)

(5)D的归一化计算公式为

假设存在个电网待恢复区域，各待恢复区域的重要性指标为(1, 2, …,)。

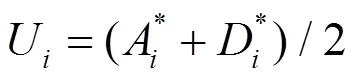
2  电网待恢复区域的重要性评估

电网待恢复区域重要性评估的流程如图3所示。

图3 电网待恢复区域的重要性评估流程图

2.1 线路介数指标

通过网络中各线路的最短路径数，即为线路介数。线路介数越大，电源节点到达负荷节点的最短路径中经过某条线路次数越多，表明该线路越重要[25]。因此线路的重要程度一定程度上可以用线路介数来描述，即

式中：B表示线路的介数；表示电网络拓扑结构中任意电源节点到负荷节点之间的最优路径数目；表示线路被电网络拓扑结构中任意电源节点到负荷节点之间最优路径经过的次数。

传统方法求解线路介数时涉及到最短路径的计算，路径的权重一般取1，求解过程方便快捷，但此种表示方法不能反映电网络的电气特性，只反映了网络拓扑特性。对于输电网，线路阻抗的大小能够反映输电线路的电气距离及运行时产生的损耗。因此，将线路阻抗的大小确定为线路权值。

2.2 线路最大输电能力

电网最大输电能力(TTC)的计算是指在基本潮流的基础上，满足各运行约束条件下，送电区域与受电区域间进行能量交换的最大值。区域到区域的最大输电能力的计算即区域发出的电量尽可能地输送给区域内的负荷[26-27]。因此可以把受电区域内的负荷有功出力之和最大值作为目标函数：

(1) 等式约束条件

(16)

(2) 不等式约束条件

3  算例分析

以 IEEE30 节点系统为例，节点系统两区域之间的联络线为线路4-12, 6-10, 9-10, 28-27，假设自然灾害造成节点 15、17、20、21、22、25 所在的电网待恢复区域内的电力设备损坏。分别用D1，D2，D3，D4，D5，D6表示各待恢复区域的名称，节点对应关系如图4所示。

图4 IEEE30节点系统

应用2.2节模型求解得到各回支路的最大输电能力归一化结果见表1。

图5和图6分别展示了算例中无故障情况下目标函数值的变化曲线和互补间隙迭代曲线。由图可以看出，迭代13次即可满足10-5的精度要求，这体现了本文方法的快速收敛性能。

应用2.1节模型求解得到各回支路的线路介数归一化计算结果见表2。

由表2的计算结果可知，作为网络中心枢纽连接线的线路介数比较高；采用了线路阻抗作为线路介数的边权值，一般情况线路阻抗大的线路介数较小，因此计及了线路阻抗的线路介数与电网络的拓扑结构更加相符。

表1 IEEE30节点系统最大输电能力(TTC)归一化计算结果

表2 IEEE30节点系统各线路的线路介数归一化计算结果

图5 目标函数值变化曲线

图6 互补间隙迭代曲线

相同线路的最大输电能力和线路介数的值存在较大差异，因为他们分别体现了电网络中输电线路的不同属性。如前文所述，结合这两个各不同的属性更能全面体现输电线路在电网络的重要程度。

IEEE30节点系统各待恢复区域的网络凝聚度及归一化计算结果见表3。

根据式(12)和式(13)得出各待恢复区域重要度及归一化结果和优先级排序结果见表4。

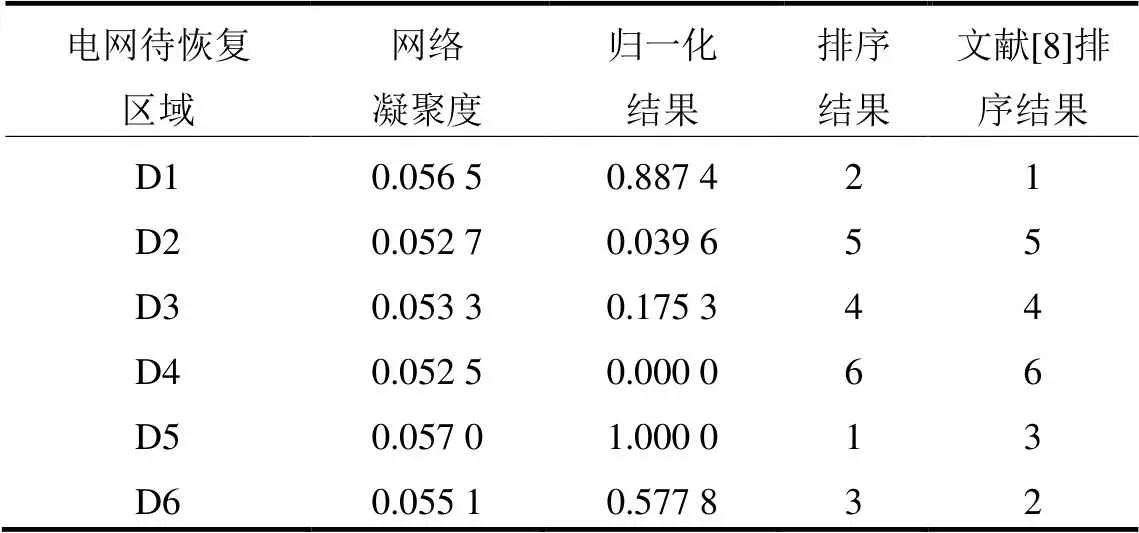
表3 各电网待恢复区域的网络凝聚度计算结果

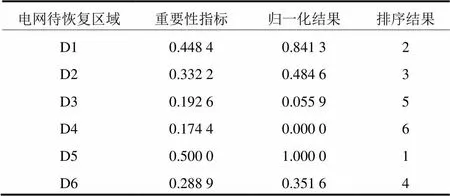
表4 各电网待恢复区域的重要性指标计算及排序结果

按照评估模型计算的结果，各电网待恢复区域的网络凝聚度指标排序结果与文献[8]的结果基本相同，其中的细小变化主要是由于评估模型考虑的因素不同造成的。文献[8]求取网络凝聚度模型中线路的边权重统一取1，而本文模型中的边权重则考虑了线路输电能力和线路介数。最后结合了功率介数加以修正最终得出待恢复区域的重要性指标。显然本文的模型更能反映电网络的电气特性，与实际情况更相符。

4  结语

对电网待恢复区域进行重要性评估对于灾后电网恢复策略的制定具有重要意义。针对已有评估模型中介数指标的不足和考虑因素单一的问题，本文将复杂网络的共性与电网络的特性相结合，提出了综合考虑输电线路输电介数和节点功率介数的电网待恢复区域重要性评估模型，能对电网待恢复区域的重要性作出较为全面的评估。

通过IEEE-30节点系统进行了详细的仿真计算。得出待恢复区域的重要性指标从而确定了待恢复区域的物资需求优先级，可以给电力应急体系中的物资调度提供参考。

[1] 尚敬福, 张瑜, 张建华. 电力应急物资联合储备管理系统设计[J]. 能源技术经济, 2010, 22(6): 57-60.

SHANG Jingfu, ZHANG Yu, ZHANG Jianhua. Design of the integrated reserve management system for electric power emergency materials[J]. Energy Technology and Economics, 2010, 22(6): 57-60.

[2] 陈曦. 基于风险理论的电力系统静态安全性评估方法研究[D]. 武汉: 华中科技大学, 2012.

[3] 受灾电网基本恢复供电[EB/OL]. http://www.csg.cn/nw gsxw/2013/mtgz/201305/t20130521_61529.html.

[4] "威马逊"减弱62.5%受影响用户恢复供电[EB/OL]. http: //www.csg.cn/index/dbt/201407/t20140721_83961.html

[5] 威马逊超强台风造成琼粤桂295亿损失20人死亡[EB/OL].http://www.takefoto.cn/viewnews-110167.html.

[6] 梁颖, 方瑞明, 卢小芬, 等. 基于复杂网络理论的电力系统脆弱线路辨识研究现状[J]. 电力系统保护与控制, 2012, 40(20): 151-155.

LIANG Ying, FANG Ruiming, LU Xiaofen, et al. Search status of power system vulnerable line identification based on complex-network theory[J]. Power System Protection and Control, 2012, 40(20): 151-155.

[7] 刘文颖, 梁才, 徐鹏, 等. 基于潮流介数的电力系统关键线路辨识[J]. 中国电机工程学报, 2013, 33(31): 90-98.

LIU Wenying, LIANG Cai, XU Peng, et al. Identification of critical line in power systems based on flow betweenness[J]. Proceedings of the CSEE, 2013, 33(31): 90-98.

[8] 苏慧玲, 李扬. 基于电力系统复杂网络特征的线路脆弱性风险分析[J]. 电力自动化设备, 2014, 34(2): 101-107.

SU Huiling, LI Yang. Analysis of complex network characteristics based on quasi-steady PTDF for power system[J]. Electric Power Automation Equipment, 2014, 34(2): 101-107.

[9] 刘艳, 顾雪平．基于节点重要度评价的骨架网络重构[J]. 中国电机工程学报, 2007, 27(10): 20-27.

LIU Yan, GU Xueping. Node importance assessment based skeleton network reconfiguration[J]. Proceedings of the CSEE, 2007, 27(10): 20-27.

[10] 陈晓刚, 孙可, 曹一家. 基于复杂网络理论的大电网结构脆弱性分析[J]. 电工技术学报, 2007, 22(10): 138-144.

CHEN Xiaogang SUN Ke, CAO Yijia. Structural vulnerability analysis of large power grid based on complex network theory[J]. Transactions of China Electrotechnical Society, 2007, 22(10): 138-144.

[11] 王凯. 基于复杂网络理论的电网结构复杂性和脆弱性研究[D]. 武汉: 华中科技大学, 2011.

[12] 谢琼瑶, 邓长虹, 赵红生, 等. 基于有权网络模型的电力网节点重要度评估[J]. 电力系统自动化, 2009, 33(5): 21-24.

XIE Qiongyao, DENG Changhong, ZHAO Hongsheng, et al. Evaluation method for node importance of power grid based on the weighted network model[J]. Automation of Electric Power Systems, 2009, 33(5): 21-24.

[13] BOMPARD E, NAPOLI R, XUE F. Analysis of structural vulnerabilities in power transmission grids[J]. International Journal of Critical Infrastructure Protection, 2009, 2(1-2): 5-12.

[14] 鞠文云, 李银红. 基于最大流传输贡献度的电力网关键线路和节点辨识[J]. 电力系统自动化, 2012, 36(9): 6-12.

JU Wenyun, LI Yinhong. Identification of critical lines and nodes in power grid based on maximum flow transmission contribution degree[J]. Automation of Electric Power Systems, 2012, 36(9): 6-12.

[15] 杨旭昕, 刘俊勇, 季宏亮, 等. 应急电力物资综合调配方案模型设计[J]. 电力系统及其自动化学报, 2011, 23(2): 85-91.

YANG Xuxin, LIU Junyong, JI Hongliang, et al. Design of emergency power material allocation model[J]. Proceedings of the CSU-EPSA, 2011, 23(2): 85-91.

[16] 罗华峰, 房鑫炎, 俞国勤. 考虑负荷顺位的电力应急资源调度模型[J]. 中国电力, 2013, 46(9): 107-111.

LUO Huafeng, FANG Xinyan, YU Guoqin. Power emergency resources allocation schedule model considering the sequence of loads[J]. Electric Power, 2013, 46(9): 107-111.

[17] 詹昕, 向铁元, 陈红坤, 等. 基于搜索矢量拟态物理学算法的微电网脆弱性评估及重构[J]. 电工技术学报, 2014, 29(2): 74-81.

ZHAN Xin, XIANG Tieyuan, CHEN Hongkun, et al. Vulnerability assessment and reconfiguration of microgrid based on search vector artificial physics optimization algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 74-81.

[18] 李迁, 李华强, 黄昭蒙, 等. 基于暂态能量函数混合法的电力系统脆弱性分析[J]. 电力系统保护与控制, 2013, 41(20): 1-6.

LI Qian, LI Huaqiang, HUANG Zhaomeng, et al. Research status of power system vulnerable line identification based on complex-network theory[J]. Power System Protection and Control, 2013, 41(20): 1-6.

[19] 王涛, 高成彬, 顾雪平, 等. 基于功率介数的电网关键环节辨识[J]. 电网技术, 2014, 38(7): 1907-1913.

WANG Tao, GAO Chengbin, GU Xueping, et al. Power betweenness based identification of power grid critical links[J]. Power System Technology, 2014, 38(7): 1907- 1913.

[20] 刘小丽, 毛弋, 梁杉, 等. 基于综合介数的电网脆弱线路辨识[J]. 电力系统保护与控制, 2016, 44(2): 116-121.

LIU Xiaoli, MAO Yi, LIANG Shan, et al. Identification of vulnerable lines in power grid based on comprehensive betweenness index [J]. Power System Protection and Control, 2016, 44(2): 116-121.

[21] 曾瑛, 朱文红, 邓博仁, 等. 基于电网影响因子的电力通信网关键节点识别[J]. 电力系统保护与控制, 2016, 44(2): 102-108.

ZENG Ying, ZHU Wenhong, DENG Boren, et al. Crucial node decision algorithm based on power network impact factor in electric power communication network[J]. Power System Protection and Control, 2016, 44(2): 102-108.

[22] 程向辉, 刘俊勇, 冯翰, 等. 计及多因素的电力应急物资储备库选址方法[J]. 电力系统及其自动化学报, 2012, 24(3): 80-85.

CHENG Xianghui, LIU Junyong, FENG Han, et al. Location method of electricity emergency material storage considering multiple factors[J]. Proceedings of the CSU-EPSA, 2012, 24(3): 80-85.

[23] 汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006.

[24] ZHANG Guohua, WANG Ce, ZHANG Jianhua, et al. Vulnerability assessment of bulk power grid based on complex network theory[C] // Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, 2008: 1554-1558.

[25] 王亮, 刘艳, 顾雪平, 等. 综合考虑节点重要度和线路介数的网络重构[J]. 电力系统自动化, 2010, 34(12): 29-33.

WANG Liang, LIU Yan, GU Xueping, et al. Skeleton- network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems, 2010, 34(12): 29-33.

[26] 陈碧云. 基于现代内点理论的电力系统最优化问题研究[D]. 南宁: 广西大学, 2003.

[27] 汪峰, 白晓民. 基于最优潮流方法的传输容量计算研究[J]. 中国电机工程学报, 2002, 22(11): 36-41.

WANG Feng, BAI Xiaomin. OPF based transfer capability calculation[J]. Proceedings of the CSEE, 2002, 22(11): 36-41.

(编辑 周金梅)

Importance evaluation of electric power areas to be restored considering electricity transmission betweenness and power betweenness

CHEN Biyun, YE Renhuan, BAI Xiaoqing

(Guangxi Key Laboratory of Power System Optimization and Energy Technology (Guangxi University), Nanning 530004, China)

When faults in the large scale power systems are triggered by natural disaster, it is necessary to assess the importance of areas which need to be restored for developing restoration strategies. Due to the shortcoming of betweenness indices for the existing evaluation model, the concept of electricity transmission betweenness is proposed, combining what the complex networks have in common and the electrical characteristics of electrical network and considering the betweenness and the maximum transmission capacity of transmission lines. And then, network condensation degree of each area to be restored is calculated. According to the power characteristics of the generators and loads, the node power betweenness is used to correct the network aggregation index, and the priority, as well as importance index, of the area to be restored is obtained, which can be used as a reference for emergency dispatching system of power supplies. Finally, a simulation based on standard IEEE system is implemented to verify the feasibility and applicability of the proposed method. This work is supported by National Natural Science Foundation of China (No. 51107011).

importance of areas to be restored; network condensation degree; electricity transmission betweenness; node power betweenness

10.7667/PSPC150911

国家自然科学基金项目(51107011)

2015-06-02；

2016-01-24

陈碧云(1978-)，女，博士，副教授，主要研究方向为电力系统规划与可靠性；叶仁欢(1988-)，男，通信作者，硕士研究生，主要研究方向为电力系统规划与可靠性；E-mail: rehuany@163.com 白晓清(1969-)，女，博士，副教授，主要研究方向为电力系统最优化。