电压偏差和谐波约束下配网光伏最大渗透率评估

黄 巍，吴俊勇，鲁思棋，郝亮亮



电压偏差和谐波约束下配网光伏最大渗透率评估

黄 巍，吴俊勇，鲁思棋，郝亮亮

(北京交通大学，北京 100044)

针对多个三相不平衡配电网络，在不同位置接入分布式光伏，运用OpenDSS软件计算了分布式光伏接入配网后节点电压偏差及谐波电压畸变率。根据ANSI C84.1-2006稳态电压标准以及IEEE519-1992谐波标准对电压偏差和谐波电压畸变率进行约束，得出不同位置下稳态电压偏差和谐波约束下分布式光伏的最大渗透率，同时分析了线路调压器及光伏接入点短路容量与光伏渗透率的关系。研究结果表明，光伏渗透率与具体配电网的拓扑结构和线路参数相关，光伏接入点越靠近馈线首端，渗透率越大。同时考虑电压偏差和谐波约束下光伏渗透率至少能达到20%，并且使线路调压器与其下游接入的光伏发电功率协调配合也可显著提高光伏的渗透率。

分布式光伏；配电网；电压偏差；谐波；渗透率

0 引言

在传统的配电网中接入分布式电源会对电网的安全稳定和电能质量带来影响[1-4]，如何分析DG对系统的影响以及确定在某一给定约束下的最大安装容量越来越受到关注。

目前，针对分布式电源接入实际配电网进行系统讨论的文献比较少[5]，大多是基于光伏系统本身的控制来展开研究。文献[6]建立了光伏并网逆变器的EL功率模型，利用阻尼注入方法设计了光伏并网系统。文献[7]提出功率控制调节系数算法，建立电压不平衡下光伏发电的谐波电流抑制策略，并通过PSCAD平台验证了方案的有效性。文献[8]针对光伏逆变器进行研究，提出了一种新型无变压器型单相光伏逆变器。在实际配电网中，分布式光伏所占比例越来越大，尤其是在配电网负荷建筑物上安装分布式光伏电源，使得配电网变成了环形网络，而实际配电网普遍存在三相不平衡现象，此时，对于一个给定的实际配电网确定稳态电压偏差和谐波电压约束下的光伏最大渗透率对于配电网的规划和运行显的尤为重要。

从谐波分析的角度，在理想配电网中不同位置接入不同容量和模型的DG时，系统谐波电压的畸变水平与DG接入位置、DG容量和DG的谐波源模型有关[9-10]。文献[11]通过一个简单的系统，建立了不同负荷分布规律下的谐波电压畸变率计算模型，并根据IEEE519-1992标准分别算出7次谐波和9次谐波约束下的分布式电源的最大渗透率，得出最大渗透率可以达到馈线容量的100%。文献[12]把谐波约束下的逆变型分布式电源的最大渗透率抽象成一个混合整型非线性规划问题，并通过粒子群算法求解得出谐波电压约束下的分布式电源的最大容量。

从电压偏差的角度，在传统配电网中接入DG会导致接入点处过电压，而DG对配电网电压的影响与DG的容量以及DG的安装位置密切相关[13-15]。文献[16]从电网电压降落的角度研究光伏发电接入配电网前后电网电压的变化，并提出了解决分布式光伏发电引起电压越限的措施和方案。在电压约束下的DG最大接入容量方面，文献[17]针对不同典型的负荷分布，计算得出考虑过电压约束下的分布式光伏电源的准入容量。文献[18]提出了考虑电压调整约束后的准入功率计算模型。该模型的特点是能够模拟有载调压变压器、分布式电源事故停运以及多个分布式电源的情况。文献[19]推导出了6种典型分布情况下线路电压偏差和电压波动不越限时分布式光伏最大容量，并在此基础上定义了光伏可接入容量极限的概念。

在已有成果的基础上，本文通过对IEEE123、IEEE37、IEEE13三个不同规模的典型三相不平衡配电网络，在不考虑增加额外无功补偿或者调压设备的前提下，在不同位置接入分布式光伏发电装置，逐渐增加光伏的容量，得出不同系统在电压偏差和谐波约束下能够达到的光伏最大渗透率。

1  理论分析

1.1 电压和谐波分析

分布式光伏是指分布在负荷附近，将太阳能转化为电能的小型环保发电设施。 一般由光伏发电环节、逆变环节以及电网侧滤波环节等部分组成。同时为了最大限度地利用光照资源，分布式光伏通常工作在最大功率点跟踪模式(MPPT)以及单位功率因数状态，在分析中，将光伏视为一个纯有功功率电源。

光伏接入到配电网以后，根据IEEE1547相关标准的规定，光伏不参与电压调节。当光伏接入到配电网以后，由于光伏有功功率的输出，能够改变线路上传输的功率，从而改变节点电压的大小。光伏有功输出越大，对电压的影响越显著。

从谐波建模和仿真的角度，一个光伏可以看作是一种向配电馈线注入谐波的非线性负荷，经过功率变换器接入电网的光伏会产生谐波电流，如果光伏在某个时刻产生的谐波电流足够大，配电网的电压畸变率会超过IEEE519-1992标准规定的畸变限值。

本文通过在给定电网中不同的位置逐渐增加光伏的安装容量，在一天时间内观察给定电网的负荷节点的电压和谐波电压畸变率是否超过了ANSI C84.1-2006电压标准和IEEE519-1992谐波标准规定的限值。

1.2 光伏模型

仿真采用EPRI开发的OpenDSS软件，OpenDSS是一个三相不平衡潮流计算软件，光伏采用OpenDSS内部提供的光伏系统模型，光伏阵列输出的功率取决于光照强度以及温度，每个光伏工作在单位功率因数和最大功率点跟踪模式(MPPT)。图1给出了安装容量为139 kVA的光伏一天时间内的功率输出曲线。

在谐波潮流计算中，光伏的谐波源特性根据IEC 61727-2004(光伏并网接口特性)标准设置光伏系统的各次谐波输出参数，通过潮流计算，得出一天之内随着光照强度和温度变化的负荷节点的电压畸变率以及电压偏差。

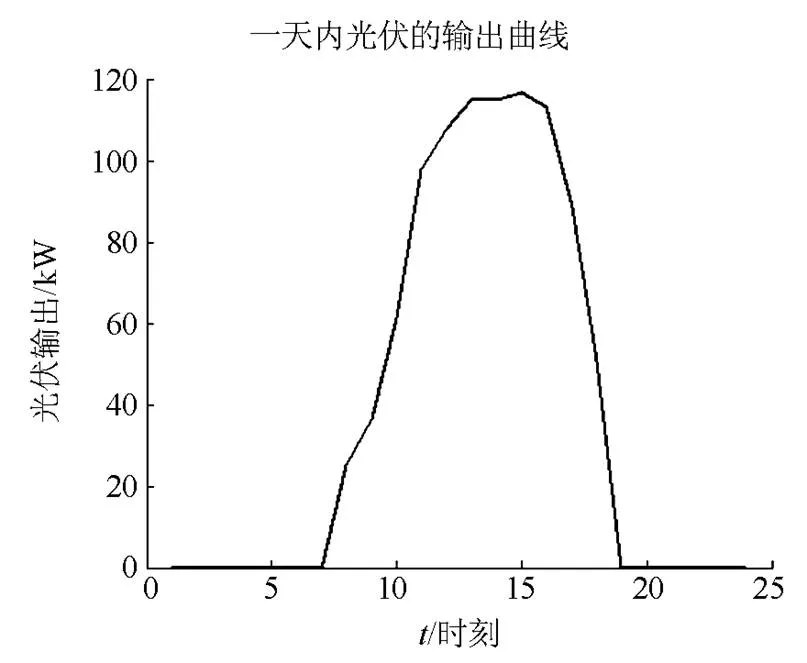
图1 光伏一天时间内的功率输出变化曲线

1.3 配电网络与负荷

实际配电网由于系统负荷不平衡，或者对地电容不均衡都会导致配电网出现三相不平衡情况，而且实际配电网的拓扑结构和参数千差万别，因此研究多个给定的实际配电网的光伏最大渗透率并从中总结规律，对于配电网的规划和运行具有指导意义。因此，本文选取IEEE123、IEEE37、IEEE13节点系统作为研究对象。IEEE系统属于多节点多分支树状配电网络，网络中的负荷种类繁多，包括两相负荷，三相负荷。为了调节电压，维持电压在给定的范围内IEEE系统都含有单相或者三相调压器。为了便于研究，不考虑负荷在一天之内的随机特性，同时将变电所以上的电压等级都等效成一个电压源。

1.4 光伏的位置选取

定义光伏的渗透率为光伏的总安装容量与配电网所有负荷的峰值视在功率的比值。

为了研究不同位置接入分布式光伏对配电网的影响，首先对给定系统，对所有负荷节点按照与馈线电源的距离进行排序，负荷与馈线首端的距离通过输电线路的长度计算得出，以到馈线首端的距离的最小值和最大值为端点，将整个区间等分成三等份。取位于区间前三分之一的负荷节点接入光伏为“首端”接入方案；位于配电网中间三分之一的负荷节点接入光伏为“中部”接入方案；位于配电网后三分之一的负荷节点接入光伏为“末端”接入方案；“均匀”分布方案是指在所有负荷节点上接入光伏，“随机”分布方案是将负荷节点到馈线电源的距离进行随机排序，根据不同系统的负荷节点的个数，取前面若干个节点接入光伏。如对于IEEE123节点算例，负荷节点到馈线电源的距离的最小值为400英尺，到馈线电源的距离的最大值为6 225英尺，将区间[400，6 225]等分成三段，负荷节点到电源的距离位于前三分之一段为馈线首端，负荷节点到电源的距离位于中间三分之一段范围内的为馈线中部，距离位于后面三分之一的范围内为馈线末端。由于仿真算例属于多分支配电树状网络，馈线末端的负荷节点也有可能属于同一距离但是不同分支的线路上。同时为了充分研究给定系统的光伏渗透率，对于随机分布情况，每一个系统仿真三种光伏随机分布的情况。

通过馈线首端、中部、馈线末端，均匀分布以及随机分布五种典型的位置，在负荷节点上接入光伏，不断地增加光伏的渗透率，观察一天之内含光伏配电网的负荷节点电压和谐波畸变率，直到一天之内某个时刻配电网的某个负荷节点电压偏差或者谐波电压畸变率越限。在考虑谐波影响的光伏渗透率时，不考虑非线性负荷产生的谐波的影响。取光伏渗透率按15%递增，接入每个负荷节点的光伏按照某种接入位置下每个负荷节点的容量占总负荷容量的比例进行分配，不断地提高渗透率，直到电压偏差或者谐波畸变率越限。

2  算例分析

在IEEE系统中根据上述位置接入光伏，仿真得出某个位置和容量下光伏运行一天的负荷节点电压和谐波畸变率，并找出一天之内电压和谐波电压畸变率的最大值，直到电压和谐波畸变率超过了ANSI C84.1-2006稳态电压标准以及IEEE519-1992谐波标准下的限值。

2.1 IEEE123节点算例评估

在IEEE123节点算例中，有四个调压器，两个三相调压器，两个单相调压器，同时在馈线末端区域包含四个接地电容，通过提供容性无功功率实现对末端电压的支撑。在馈线首端，馈线中间，馈线末端，均匀以及三种随机分布的位置下接入分布式光伏，不同位置下，考虑电压和谐波约束的光伏最大渗透率仿真结果如图2所示。由图可见，在IEEE123节点配网中，电压偏差指标成为限制光伏最大渗透率进一步提高的主要瓶颈；即使不采取任何措施，该配电网的最大光伏渗透率也在30%以上。

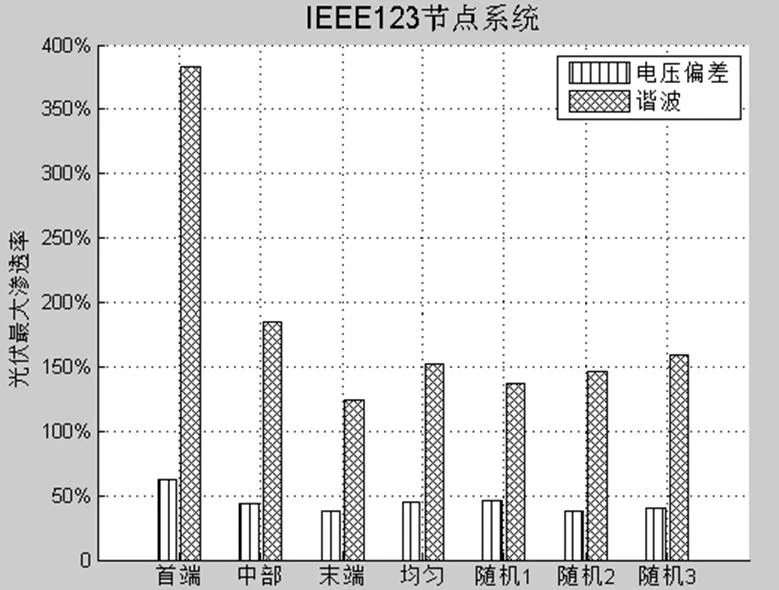
图2 IEEE123节点光伏最大渗透率

2.2 IEEE37节点算例评估

IEEE37节点系统含有两个单相调压器，均位于主配电变压器下侧，不含固定电容器。考察光伏渗透率与电压偏差和谐波的关系。不同位置下的仿真结果如图3所示。由图可见，在IEEE37节点配电网中，谐波指标成为限制光伏最大渗透率进一步提高的主要瓶颈；即使不采取任何措施，该配电网的最大光伏渗透率也在20%以上。

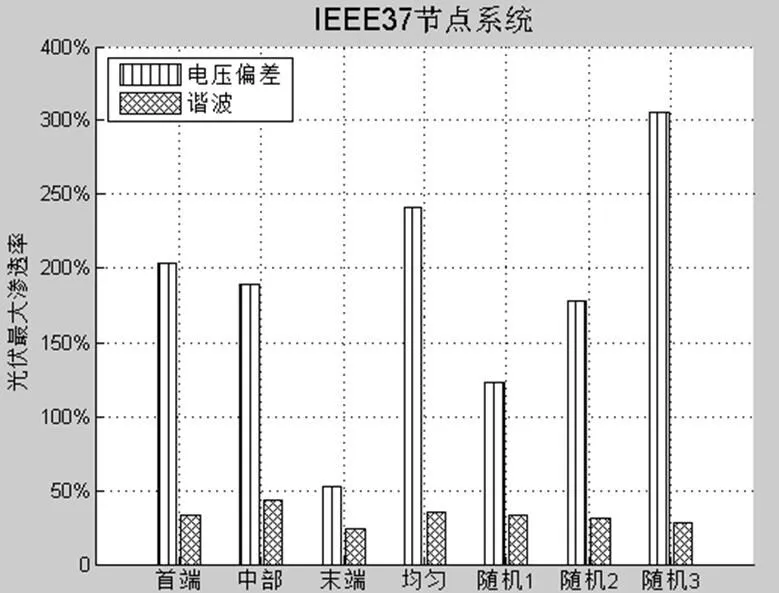
图3 IEEE37节点光伏最大渗透率

2.3 IEEE13节点算例评估

IEEE13节点系统含有一个单相调压器，位于主配电变压器下侧，含两个固定电容器，一个三相电容器以及一个单相电容器。不同位置下的仿真结果如图4所示。由图可见，在IEEE13节点配电网中，电压约束和谐波约束下的光伏渗透率均能达到50%以上，谐波约束下的光伏渗透率能达到100%，电压和谐波指标此时并不是限制光伏渗透率进一步提升的瓶颈，但是不同位置下的光伏渗透率各有不同。

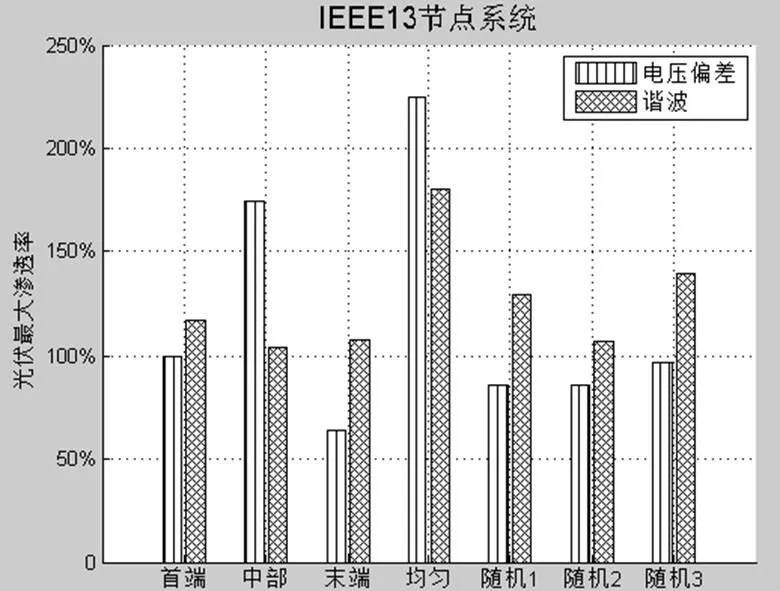
图4 IEEE13节点光伏最大渗透率

2.4 不同系统进行比较

取电压偏差和谐波约束下的光伏渗透率的较小值作为该系统的光伏最大渗透率，即

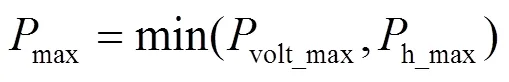
不同系统的光伏渗透率结果如图5所示。

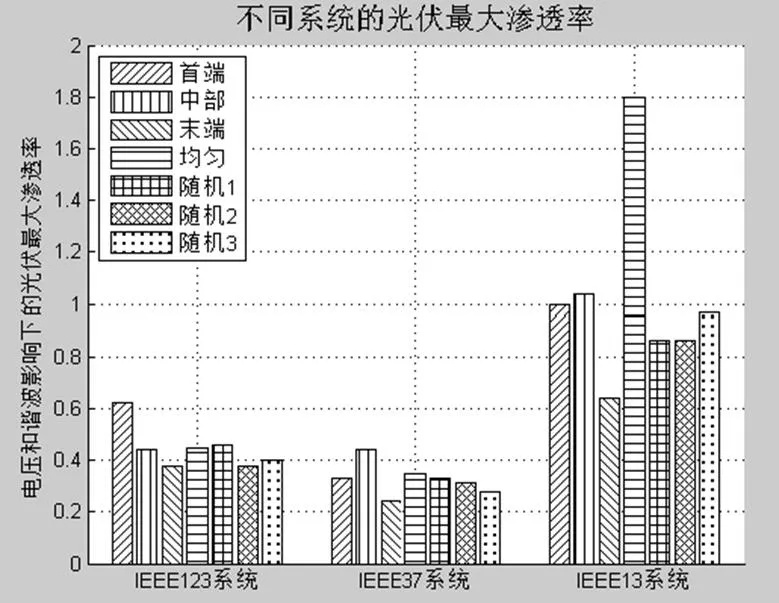
图5 不同系统的光伏最大渗透率

3  分布式光伏数据结果分析

不同的系统在电压和谐波约束下的光伏最大渗透率相差比较大，反映出了不同系统的馈线结构的差异。同一系统不同位置上的光伏最大渗透率也相差较大。

IEEE123系统考虑谐波约束的渗透率显著高于电压约束下的渗透率，其中首端位置下的光伏渗透率最大，末端最低，图2中首端位置下谐波约束下的光伏最大渗透率能达到380%，意味着此时谐波指标不是光伏渗透率的主要限制因素。

对IEEE37系统而言，谐波和电压约束的光伏最大渗透率与IEEE123系统相反，谐波指标成为限制光伏渗透率的主要因素，但是考虑电压和谐波双重因素的光伏渗透率与IEEE123系统近似。可以看出，不论是谐波还是电压，末端接入的光伏渗透率依然是最小，均匀分布情况下的光伏最大渗透率都比较大。

在IEEE13节点系统中，电压与谐波约束下的光伏渗透率能达到50%以上，说明对于此系统，电压和谐波指标并不是限制光伏渗透率的主要因素。

图5结果显示，对于不同系统，同时考虑电压偏差和谐波约束下的光伏最大渗透率至少能够达到20%以上，这对于实际电网光伏及分布式电源规划具有指导意义。

从仿真结果来看，不论是电压约束还是谐波约束，在末端位置下接入光伏的渗透率总是最小的，而首端位置和中部位置下的光伏要显著高于末端位置下的光伏渗透率。光伏接入末端位置时，电压变化更显著，因此，一般情况下，光伏接在末端下的渗透率要小于接在首端和中部位置下的光伏渗透率。

如图6所示，分别在IEEE37节点首端和末端接入相同渗透率的光伏，可以看出，不接光伏时，末端电压已经越下限了，接入光伏之后，末端位置下配电网电压抬升效果显著高于首端位置下。

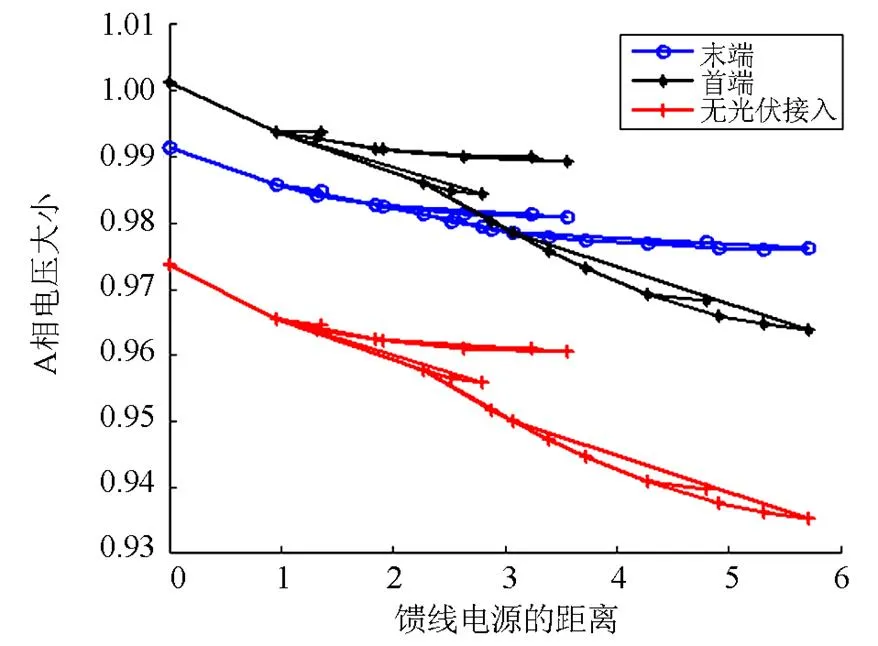
图6 光伏渗透率为30%时IEEE37节点A相电压变化

在仿真中，均匀分布下的光伏的渗透率都非常大，此时光伏在馈线系统中的分散度相对于其他位置下的光伏明显增大，说明在给定配电网中，光伏接入的分散度越高，渗透率越大。

综上所述，对于电压偏差和谐波电压约束下的光伏渗透率，光伏的接入位置一定时，光伏总出力占负荷比值越大，电压抬升的越高，负荷节点各相电压谐波畸变率也越大。光伏的接入容量一定时，通常情况下，位置越靠近馈线末端，越容易导致电压和谐波畸变率越限。

4  电压约束条件下线路调压器与光伏的配合

IEEE123系统包括四个调压器，当不接入光伏以及不接入调压器时，IEEE123系统末端A相电压越下限，通常情况下，接入调压器或者接入一定容量的光伏时，末端电压可得到有效提升，而单独接入光伏与单独接入调压器时的末端节点电压抬升能力与光伏的容量以及SVR的参数设置有关。在含有调压器的配电网络中接入光伏，考虑稳态电压偏差上限标准，PV与SVR对某些负荷节点同时具有电压抬升能力，在SVR下游加入光伏之后，相当于等效地增大了SVR的补偿阻抗，而此时原配电网的SVR的补偿阻抗维持不变，则很有可能使负荷节点的电压越上限。若考虑调压器与下游光伏实际出力的配合，在负荷节点电压偏差已经越限的情况下，改变调压器的补偿阻抗或者调整调压器的抽头值，可进一步增大光伏的渗透率，如图7所示。

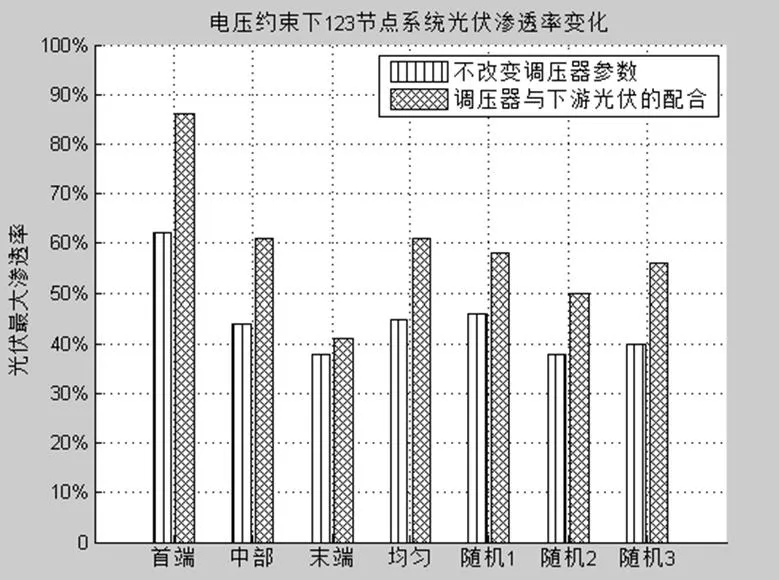
图7 考虑调压器与光伏配合后的光伏渗透率的变化

5  谐波约束下光伏渗透率分析

谐波约束下的光伏渗透率与电压约束下的光伏渗透率在位置上的分布规律类似，末端位置接入情况下的光伏渗透率总是小于首端和中部位置下的光伏渗透率。

IEEE123系统和IEEE37系统谐波约束下的光伏渗透率相差很大，说明谐波约束下的光伏渗透率与不同系统的馈线构造相关。随着光伏渗透率的增大，负荷节点的电压谐波畸变率呈现单调递增上升趋势，与含有SVR的配电网的电压的变化趋势略有不同。在含有非线性分布式电源的配电网中，当分布式电源距离系统母线越远，分布式电源总出力越多，则配电网谐波电压的畸变水平就越大。

6  短路容量与光伏渗透率的关系

实际情况中，在根据并网确定DG的装机容量时，通常采用基于并网点短路容量的方法[20]。并网点短路容量越大，表明网络强，负荷等设备的投切不会引起电压幅值或者其他电能指标的变化，基于此，对IEEE的三个系统的不同位置下的负荷节点处求出各负荷节点的短路容量，并求出各个位置下负荷节点的短路容量的平均值，以表征该位置下的短路容量。同时，对不同位置下的短路容量与不同位置下电压和谐波约束下的光伏渗透率进行相关性分析，计算观察短路容量与不同指标下的光伏渗透率的线性相关性，如表1和表2所示。

表1 电压约束下光伏最大渗透率与不同位置下短路容量的相关性系数

Table 1 Correlation coefficient of maximum penetration and PV maximum penetration in several scenarios with voltage considerations

表2 谐波约束下光伏最大渗透率与不同位置下短路容量的相关性系数

Table 2 Correlation coefficient of maximum penetration and PV maximum penetration in several scenarios with harmonic considerations

从表1、表2可以看出，电压约束下的光伏渗透率与短路容量呈现正相关的关系，说明相同容量的光伏接入短路容量越大的位置，对电压偏差影响越小；而短路容量对于谐波约束下的光伏渗透率影响不显著，不同的系统相差较大。

7  结论

本文针对三个典型的不平衡配电网络，在不同位置接入光伏电源，得出考虑电压偏差和谐波约束下的光伏最大渗透率，并分析了不同位置下分布式光伏接入配网后电压和谐波畸变率的变化规律，得出以下结论：

(1) 一定容量的光伏接入配电网络，会对馈线上的电压和谐波产生重大影响，随着光伏容量的增大，会对馈线上的电压产生抬升作用，同时，负荷节点的谐波电压畸变率也随着光伏容量的增大而单调递增。

(2) 对于谐波和电压约束下的光伏渗透率，光伏接入位置越靠近馈线首端，最大渗透率越大，越接近配网末端，允许的最大渗透率越小。实际配电网的光伏接入位置应尽量靠近配电变压器侧，有利于减小对配电网的不利影响。

(3) 实际配电网都含有一个或者多个调压器，通过改变分接头来维持末端电压在额定值附近。当分布式光伏接入配电网以后，调压器的参数需要根据其下游接入光伏的实际出力协调配合，比如分接头的调整或者补偿阻抗的重新整定，实现在同样的电压抬升效果下，增大光伏的渗透率。

(4) 均匀分布下的光伏对于电压和谐波约束的最大渗透率显著高于各种集中光伏接入方案的渗透率，说明分布式光伏接入位置的分散度越大，对配电网的影响也越小，渗透率也越大。

(5) 不同系统电压约束下光伏的渗透率与不同位置的短路容量显著相关，谐波约束下的光伏渗透率在不同的系统与短路容量的相关性不显著，与具体系统的馈线结构参数相关。

(6) 不同系统由于配网结构和参数不同，影响最大光伏渗透率的约束也不同。从仿真结果上看，对于各种结构的配电网，考虑电压和谐波约束下的光伏渗透率至少能达到20%以上。

[1] 王一波, 李晶, 许洪华, 等. 考虑电网安全稳定约束的光伏最大安装容量计算与分析[J]. 太阳能学报, 2008, 29(8): 971-975.

WANG Yibo, LI Jing, XU Honghua, et al. Calculation and analysis of maximum photovoltaic capacity considering the security and stability of power grid[J]. Journal of Solar Energy, 2008, 29(8): 971-975.

[2] 周林, 曾意, 郭珂, 等. 具有电能质量调节功能的光伏并网系统研究进展[J]. 电力系统保护与控制, 2012, 40(9): 137-145.

ZHOU Lin, ZENG Yi, GUO Ke, et al. Development of photovoltaic grid-connected system with power quality regulatory function[J]. Power System Protection and Control, 2012, 40(9): 137-145.

[3] 张立梅, 唐巍, 赵云军, 等. 分布式发电对配电网影响的综合评估[J]. 电力系统保护与控制, 2010, 38(21): 132-135, 140.

ZHANG Limei, TANG Wei, ZHAO Yunjun, et al. The integrated evaluation of impact of distribution generation on distribution network[J]. Power System Protection and Control, 2010, 38(21): 132-135, 140.

[4] 崔红芬, 汪春, 叶季蕾, 等. 多接入点分布式光伏发电系统与配电网交互影响研究[J]. 电力系统保护与控制, 2015, 43(10): 91-97.

CUI Hongfen, WANG Chun, YE Jilei, et al.Research of interaction of distributed PV system with multiple access points and distribution network[J]. Power System Protection and Control, 2015, 43(10): 91-97.

[5] ANDERSON H, REBECCA B, JOSHUA H, et al. Steady state analysis of maximum photovoltaic penetration levels on typical distribution feeders[J]. IEEE Transactions on Sustainable Energy, 2013, 4(2): 350-357.

[6] 王久和, 慕小斌, 张百乐, 等. 光伏并网逆变器最大功率传输控制研究[J]. 电工技术学报, 2014, 29(6): 49-56.

WANG Jiuhe, MU Xiaobin, ZHANG Baile, et al.Research on maximum power transfer control of photovoltaic grid connected inverters[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 49-56.

[7] 周念成, 楼晓轩, 王强钢, 等. 电网电压不平衡下三相光伏发电系统的谐波电流抑制[J]. 电工技术学报, 2015, 30(16): 246-254.

ZHOU Niancheng, LOU Xiaoxuan, WANG Qianggang, et al. Harmonic currents suppression for three-phase photovoltaic power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 246-254.

[8] 杨晓光, 姜龙斌, 冯俊博, 等. 一种新型高效无变压器型单相光伏逆变器[J]. 电工技术学报, 2015, 30(8): 97-103.

YANG Xiaoguang, JIANG Longbin, FENG Junbo, et al. A new high efficiency transformerless single-phase photovoltaic inverter[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 97-103.

[9] 杭银丽. 分布式电源对电网谐波分布的影响及配置研究[D]. 南京: 南京理工大学, 2010.

HANG Yinli. Study on the effect of distributed generation on power grid harmonic distribution and configuration [D]. Nanjing: Nanjing University of Science and Technology, 2010.

[10] 王志群, 朱守真, 周双喜, 等. 分布式发电对配电网电压分布的影响[J]. 电力系统自动化, 2004, 28(16): 56-60.

WANG Zhiqun, ZHU Shouzhen, ZHOU Shuangxi, et al. Impact of distributed generation on distribution network voltage distribution[J]. Automation of Electric Power Systems, 2004, 28(16): 56-60.

[11] ARIJIT B, ARINDAM M, MARK H, et al. Determination of allowable penetration levels of distributed generation resources based on harmonic limit considerations[J]. IEEE Transactions on Power Delivery, 2003, 18(2): 619-624.

[12] RAVIKUMAR P, ZEINELDIN H, XIAO W E, et al. Optimal penetration levels for inverter-based distributed generation considering harmonic limits[J]. Electric Power Systems Research, 2013, 97: 68-75.

[13] 江南, 龚建荣, 甘德强, 等. 考虑谐波影响的分布式电源准入功率计算[J]. 电力系统自动化, 2007, 31(3): 19-23.

JIANG Nan, GONG Jianrong, GAN Deqiang, et al. Calculation of allowable power value of distributed generation considering harmonic constrains[J]. Automation of Electric Power Systems, 2007, 31(3): 19-23.

[14] 范元亮, 赵波, 江全元, 等. 过电压限制下分布式光伏电源最大允许接入峰值容量的计算[J]. 电力系统自动化, 2012, 36(17): 40-44.

FAN Yuanliang, ZHAO Bo, JIANG Quanyuan, et al. Calculation of maximum peak capacity of distributed generation considering voltage constraints[J]. Automation of Electric Power Systems, 2012, 36(17): 40-44.

[15] TONKOSKI R, TURCOTTE D, EL-FOULYTH M. Impact of high PV penetration on voltage profiles in residential neighborhoods[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 518-527.

[16]许晓艳, 黄越辉, 刘纯, 等.分布式光伏发电对配电网电压的影响及电压越限的解决方案[J].电网技术, 2010, 34(10): 140-146.

XU Xiaoyan, HUANG Yuehui, LIU Chun, et al. Influence of distributed photovoltaic generation on voltage in distribution network and solution of voltage beyond limits[J]. Power System Techonology, 2010, 34(10): 140-146.

[17] 刘健, 同向前, 潘中美, 等.考虑电压因素时分布式光伏电源的准入容量[J]. 电力系统保护与控制, 2014, 42(6): 45-51.

LIU Jian, TONG Xiangqian, PAN Zhongmei, et al. The maximum power of distributed PV generation according to over-voltage in distribution network[J]. Power System Protection and Control, 2014, 42(6): 45-51.

[18] 胡骅, 吴汕, 夏翔, 等. 考虑电压调整约束的多个分布式电源准入功率计算[J]. 中国电机工程学报, 2006, 26(19): 13-17.

HU Hua, WU Shan, XIA Xiang, et al.Computing the maximum penetration level of multiple distributed generators in distribution network taking into account voltage regulation constraints[J].Proceedings of the CSEE, 2006, 26(19): 13-17.

[19] 黄炜, 刘健, 魏昊焜, 等. 分布式光伏电源极端可接入容量极限研究[J]. 电力系统保护与控制, 2015, 43(3): 22-28.

HUANG Wei, LIU Jian, WEI Haokun, et al.Extreme capacity limitations of photovoltaic generators in distribution grids[J].Power System Protection and Control, 2015, 43(3): 22-28.

[20] 王伟胜, 冯双磊, 张义斌, 等. 风电场最大装机容量和电网短路容量的关系[J]. 国际电力, 2005, 9(2): 31-34.

WANG Weisheng, FENG Shuanglei, ZHANG Yibin, et al. The relationship between maximum peak capacity of wind generator and short circuit capacity of distribution network[J]. International Power, 2005, 9(2): 31-34.

(编辑 姜新丽)

Maximum photovoltaic penetration considering voltage deviation and harmonic constraints

HUANG Wei, WU Junyong, LU Siqi, HAO Liangliang

(Beijing Jiaotong University, Beijing 100044, China)

This paper interconnects distributed photovoltaic with several PV location scenarios for several unbalanced distribution system, and calculates the steady state voltage and voltage harmonic distortion with power flow program. Various levels of photovoltaic penetration are presented under the voltage constraints in the ANSI C84.1-2006 standard and the voltage harmonic distortion constraints in the IEEE519-1992 standard with several PV location scenarios. And with the simulation results of different output and different location scenarios of PV, the relationship between SVR and short circuit capacity and photovoltaic penetration is analyzed. The result of simulation shows that the penetration of photovoltaic is related with the line parameters of actual system. The closer the location of photovoltaic to the feeder source, the larger the penetration will be. For the cases considering the voltage and harmonic limits simulated, maximum photovoltaic penetration will be at least 20% of peak load, and with the coordination between SVR and the downstream PV system, the penetration of PV will be increased significantly.

distributed photovoltaic; distribution network; voltage deviation; harmonic; penetration

10.7667/PSPC150842

2015-05-19；

2015-07-06

黄 巍(1991-)，男，硕士研究生，主要研究方向为电力系统分析与控制；E-mail: 13121413@bjtu.edu.cn 吴俊勇(1966-)，男，博士，教授，博士生导师，主要研究方向为电力系统分析与控制，新能源发电和智能电网，铁道电气化，电力信息化。E-mail: wujy@bjtu.edu.cn