THM耦合作用下千枚岩隧道大变形机理

孟陆波，李天斌，杜宇本，黄志煌,3，马宏敏,4

(1.地质灾害防治与地质环境保护国家重点实验室(成都理工大学)，四川 成都　610059;2.中铁二院工程集团有限责任公司，四川 成都　610031；3.四川巴陕高速公路有限责任公司，四川 成都　610041;4.西北综合勘察设计研究院，陕西 西安　710003)

大变形是高应力软岩隧道中可能遇到的一种重大施工地质灾害。Terzaghi于1946年首次提出了挤出性岩石和膨胀性岩石的概念，受Terzaghi思想的影响，按宏观形成机制一般将隧道围岩大变形分为2类，即挤出型大变形和膨胀型大变形。如一些学者[1-7]结合某一隧道对挤出型大变形机制和预测开展了深入研究，一些学者[8-12]对膨胀型大变形机制进行了研究；同时，陈宗基[13]、Aydan O等[14]、姜云[15]等研究总结了隧道软岩大变形的类型和力学机制。可见目前对大变形机制的研究已取得较多成果，但这些研究成果基本都是针对高地应力环境下隧道软弱围岩的，而对高地应力、高地热、高渗透水压耦合作用下的岩石变形破坏机理和隧道大变形机制研究甚少。

随着西部的大开发，长大隧道越来越多，埋深越来越大，深埋地下工程的典型地质特征就是高地应力、高渗透水压、高地温(简称“三高”)，在“三高”环境下开挖软岩隧道，其围岩变形破坏机理将更加复杂，如果对其认识不清，极易引发施工地质灾害。大理—瑞丽铁路的高黎贡山隧道长34.5 km，最大埋深超过1 000 m，隧道所在地区为千枚岩软岩，并且地应力高、水热活动强烈；千枚岩是一种典型的软岩，在隧道开挖过程中，极易发生大变形。因此，本文以千枚岩这一典型软岩为研究对象，通过高地温、高渗透水压、高围压条件下千枚岩三轴卸荷试验，研究热—水—力(Thermo-Hydraulic-Mechanics，THM)耦合作用下千枚岩的变形破坏特征；以大理—瑞丽铁路高黎贡山千枚岩隧道为研究对象，采用数值模拟方法模拟千枚岩隧道的大变形；结合试验结果和数值模拟结果，探讨THM耦合作用下千枚岩隧道大变形的机理。研究结果可为高地温、高渗透水压、高地应力下的深埋软岩隧道与地下工程围岩稳定性分析提供参考。

1　THM耦合作用下千枚岩三轴卸荷试验

1.1　模拟试验方案

采用高温三轴卸荷渗透试验模拟研究THM耦合作用下千枚岩的变形破坏特征。试验设备采用MTS815Teststar程控伺服岩石力学试验机，该试验机通过加载温度模拟岩石所处的温度场、加载孔隙水压力模拟岩石所处的渗流场、加载三向应力模拟岩石所处的初始地应力，采用升轴压、卸围压的方式模拟隧道开挖过程中围岩应力的变化。

制作千枚岩圆柱体试件，直径50 mm，高100 mm，精度符合《水利水电工程岩石试验规程》(SL264—2001)[16]要求。千枚岩试件的片理面为同一个角度，总体连续性和完整性均较好，无风化现象。为分析模拟试验过程中岩石变形是否由岩石膨胀起控制作用，在高温三轴卸荷渗透试验之前先进行了矿物成分测试和自由膨胀率测试。矿物成分测试表明：千枚岩主要矿物成分为黑云母，含量占68%；其次为伊利石和石英，含量分别占10%和17%。自由膨胀率测试表明：千枚岩自由膨胀率最大值为0.07%，遇水膨胀程度低，膨胀性不是该类千枚岩变形的主控因素。

根据高黎贡山隧道地质背景，确定围压、地温等试验参数。高黎贡山隧道底板最大地温预计为45.6 ℃，最大埋深超过1 000 m，最大水平应力约为26 MPa。由此确定试验中：卸围压前的围压控制在20 MPa；地温T分别控制在20和60 ℃；渗透水压P分别控制在4和7 MPa；试件处于饱水状态。

试验过程：采用荷载控制方式，以6 MPa·min-1的加荷速度同时施加侧压力和轴向压力，直至达到预定的侧压力值并保持不变；以3 MPa·min-1的速率对试件两端施加渗透水压，直至达到预定的值并保持不变；按1 ℃·min-1的升温速度对试件加热，直至达到预定的温度并保持恒温5 h，以保证试件与炉腔温度一致；增加轴压至岩石屈服应力(取相同围压和温度的常规三轴压缩试验条件下峰值强度的70%)，之后以0.1 MPa·s-1的速率卸载围压且同时以0.1 MPa·s-1的速率增加轴压，直到试件破坏。在试验过程中，测定试件的轴向应变、横向应变、初始水压压差和最终压差。

1.2试验结果分析

1.2.1应力—应变曲线特征

试件应力—应变全过程曲线如图1所示，图中ε1为轴向应变，ε2为横向应变。由图1可得如下结论。

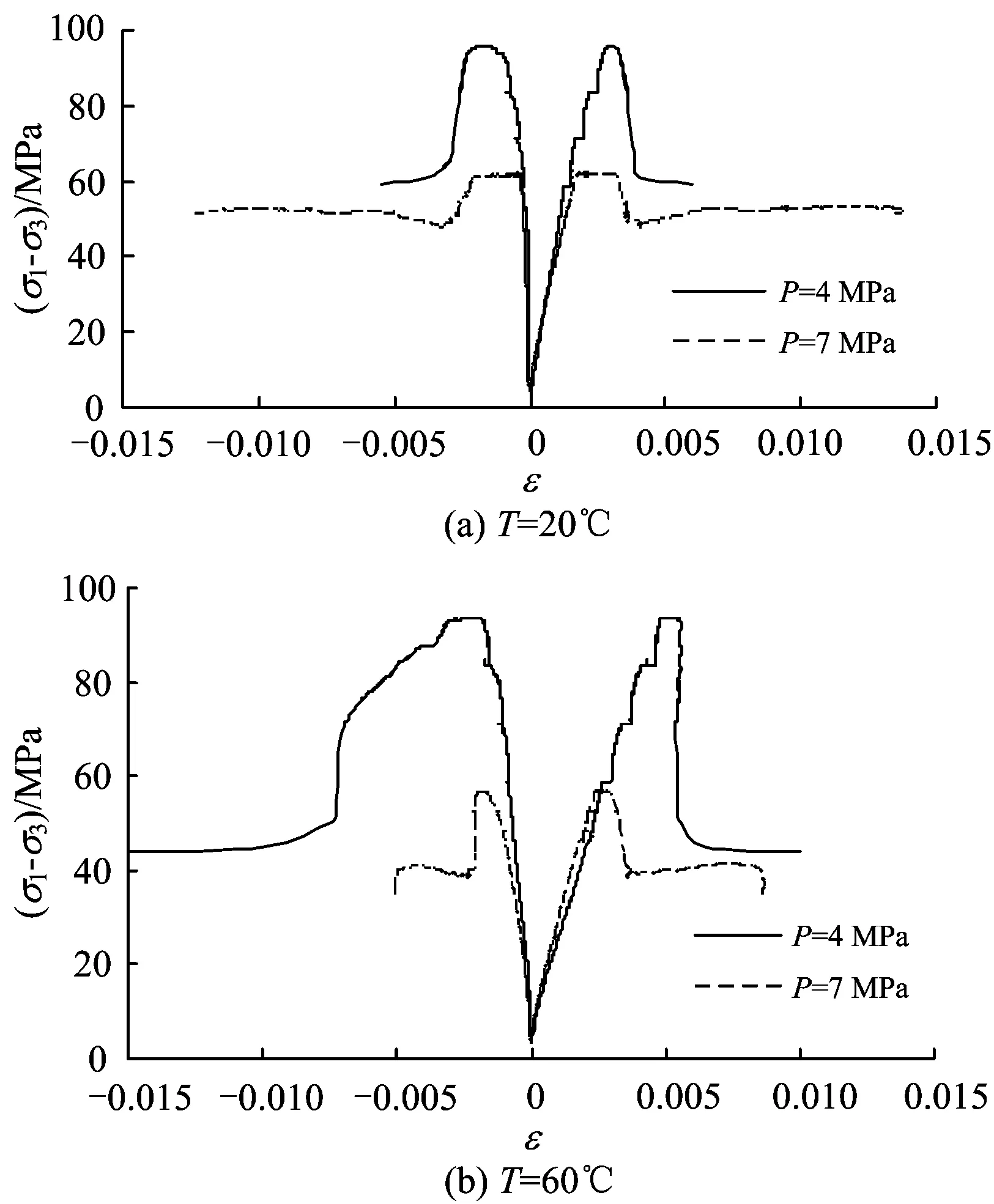
图1　试件应力—应变曲线

(1)4个试件在卸荷过程中的变形特性基本相似，岩石变形无裂隙压密阶段。变形过程可以分为3个阶段：弹性变形阶段、膨胀破坏阶段和残余变形阶段。在弹性变形阶段，轴向应变、横向应变基本呈线性增长，轴向应变ε1增长较快。在膨胀破坏阶段，横向应变偏离直线，迅速增长，并且渗透水压越高，横向应变曲线越早偏离直线段，表明岩石体积增大，表现出较强的膨胀机制。岩石破坏后，应力迅速跌落。在峰后残余变形阶段，变形进一步发展，形成宏观裂纹和破裂面。

(2)在地温一定时，随着渗透水压的增大，试件的应力峰值降低；在渗透水压作用下，岩石的应力—应变曲线更快进入了塑性变形屈服阶段。在渗透水压为4 MPa时，峰后应力—应变曲线迅速跌落，说明试件呈脆性破坏特征；当渗透水压为7 MPa时，峰后应力—应变曲线表现为应变随应力的降低而增大，说明试件具有一定的延性破坏特征。

(3)在渗透水压一定时，T=20 ℃下岩石破坏前应力-应变曲线斜率大于T=60 ℃时的曲线斜率，可见弹性模量随着地温的升高而降低；在渗透水压一定时，随着地温的升高，试件的应力峰值略有降低，如P=7 MPa条件下，T=20 ℃时试件的应力峰值为61.8 MPa，而T=60 ℃时试件的应力峰值降为56.7 MPa。

由此可得：高地温和高渗透水压对岩石均有一定的损伤，但高地温的影响小于渗透水压的影响。

1.2.2渗透率变化特征

试件体积应变的计算公式为

εv=ε1-2ε3

(1)

式中：εv为体积应变，压缩时其值为正，膨胀时其值为负；ε1为轴向应变；ε3为横向应变。

渗透率的计算公式为

(2)

式中：k为渗透率，μm2；V为试件参照体积，cm3；ΔPi/ΔPf为初始水压压差与最终水压压差之比；Δt为试验持续时间，s；Ls为试件长度，cm；As为试件横截面面积，cm2；μ为孔隙水的黏滞系数，Pa·s；β为孔隙水的压缩系数，Pa-1。

试件的轴向应变ε1与体积应变εv的关系曲线以及轴向应变ε1与渗透率k的关系曲线如图2所示。图2中A点为试件由压缩状态转为膨胀状态的临界点，即体积应变最大正值的点；B点为试件

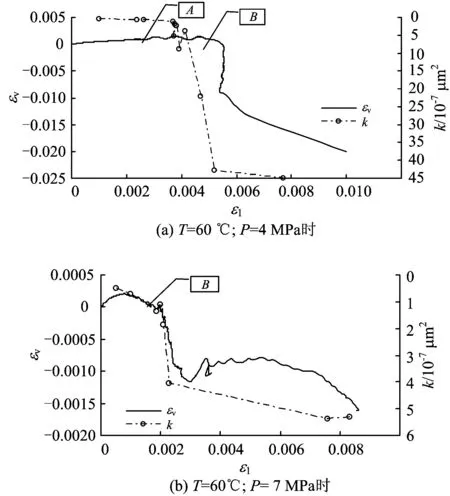
图2　轴向应变与体积应变和渗透率的关系曲线

由膨胀状态恢复至初始状态的临界点，即体积应变值为0的点。

由图2可知：在A点之前，试件处于压缩状态，这一阶段基本对应试件弹性变形阶段，岩石中的裂隙和微裂纹已被围压和高温膨胀作用挤压紧密，体积压缩，渗透性很小；在A点与B点之间，这一阶段基本对应试件膨胀破坏阶段，岩石内部新生裂隙，加之渗透水压对岩石内部的膨胀作用，渗透率逐渐增大；在B点之后，试件处于急剧膨胀状态，这一阶段基本对应试件破坏及破坏后阶段，试件体积急剧增大，膨胀强烈，渗透率发生突变，迅速增大，试件破坏后形成宏观裂纹和破裂面，渗透率保持相对大的值。由此可见，体积应变反映了试件的压缩或膨胀状态，与渗透率变化有很好的相关性。

1.2.3破裂特征

破坏后的典型试件照片如图3所示，试件宏观破坏面主要为1个贯通的剪切面，破裂角度差异不大。由于渗透水压的剪胀作用，剪切面不是平滑的剪切滑移面，而是有一定的起伏或转折，呈张剪性破坏特征。

图3　试件宏观破坏形态

对试件的典型破裂断口进行电镜扫描，微观形貌特征如图4所示。由图4可见：试件破裂断口的典型形貌基本为解理断裂，出现的花样以台阶状(见图4a)、花状(见图4b)为主。晶体中发育多组解理，与破坏应力方向垂直的解理面发生张拉破坏，形成解理张裂(见图4c)；与破坏应力方向一致的解理面发生剪切破坏，与张拉破坏复合形成沿晶张剪断裂 (见图4d)。在断口张拉破坏过程中，破坏面延伸扩展，破坏应力在约束端集中，发生剪切破坏。可见，上述千枚岩断口微观破裂机制以张剪性破坏为主，与宏观破坏特征基本一致。

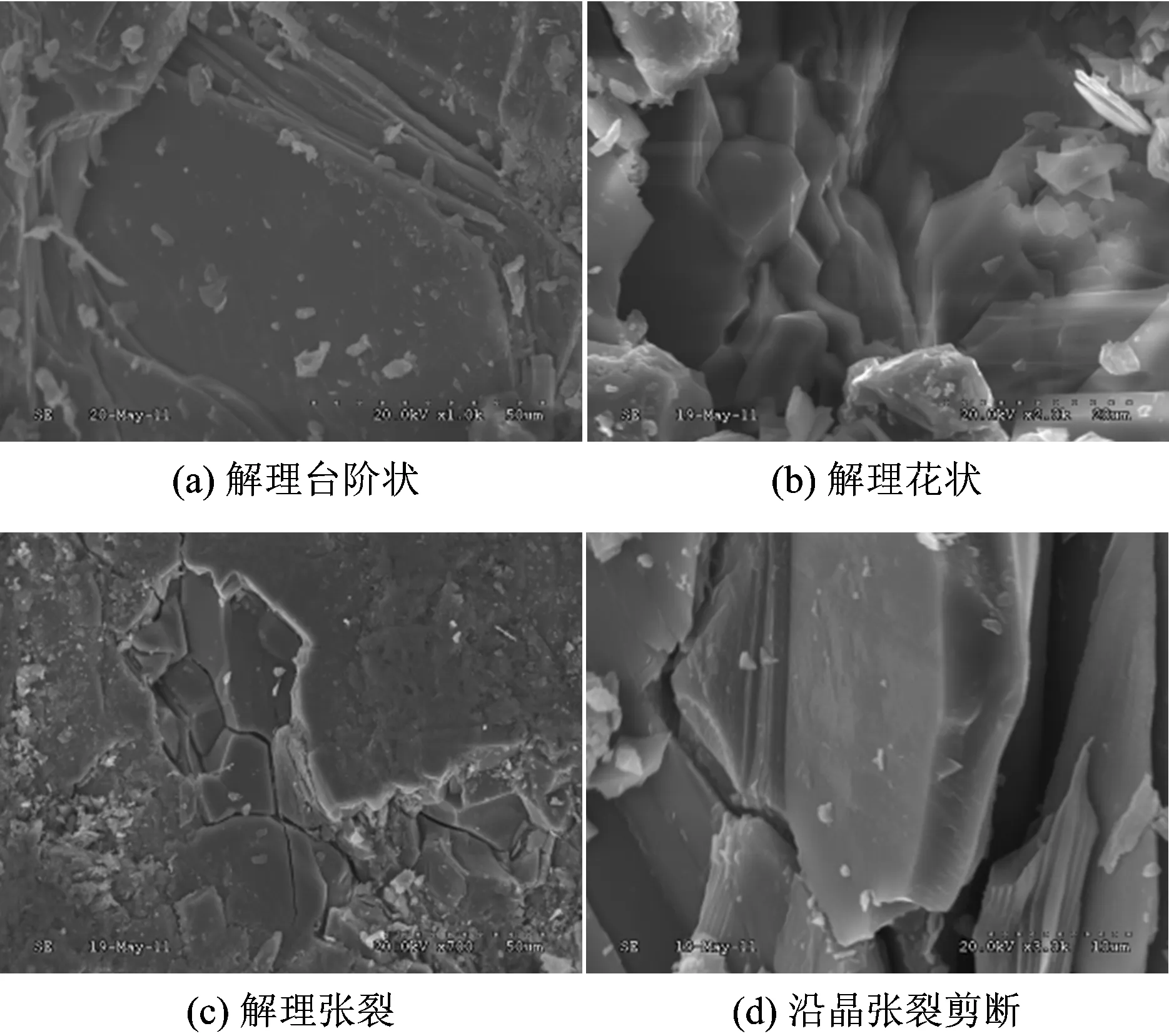
图4　典型试件断口微观形貌特征

2　THM耦合作用下软岩隧道大变形数值模拟

2.1　数值模拟模型

2.1.1模型范围

以高黎贡山隧道深埋洞身段为对象，采用COMSOL Multiphysics软件和THM耦合数学模型[17]，建立二维有限元模型，如图5所示。模型的高为80 m，宽为60 m，隧道横截面形状为马蹄形，宽为6 m，高为8 m；隧道中心线至模型两侧的距离均为30 m，隧道底部至模型下边界的距离为30 m；隧道顶部至模型上边界的距离为42 m。

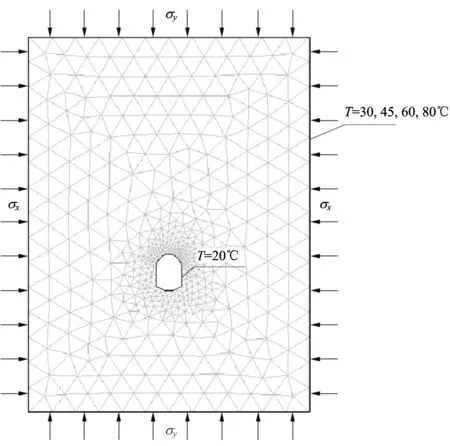
图5　二维有限元模型

2.1.2模型本构关系与计算参数

应力场本构关系设定为弹塑性，采用D-P屈服准则。千枚岩的物理力学参数见表1。

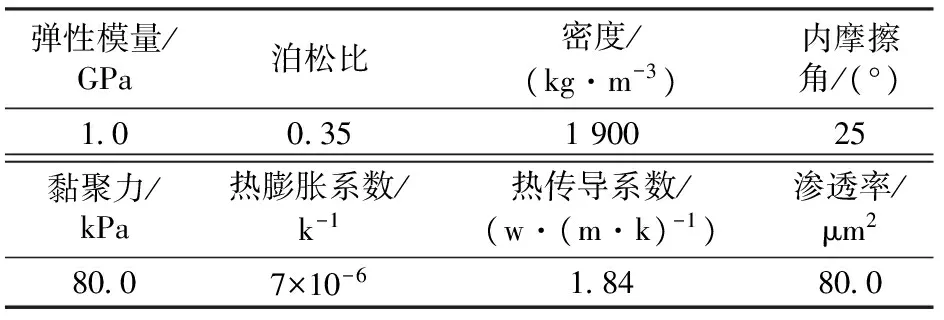
表1　千枚岩的物理力学参数

2.1.3模型边界条件

根据高黎贡山典型深埋段地质条件，在模型中设定以下边界条件。

1)温度场边界条件

计算模型四周的温度设定为岩体下度，共取4个值，分别为30 ℃(303 K)，45 ℃(318 K)，60 ℃(333 K)和80 ℃(353 K)；隧道开挖后，为达到施工要求，隧道内必然采取通风等措施对隧道降温，因此计算牛型隧道内部的温度设定为降温后的温度，为20 ℃(293 K)。

2)渗流场边界条件

计算模型的左、右边界设定为不透水边界，上边界和下边界分别赋予不同的水头，水头差500 m；隧道边界设定为不透水边界。

3)应力场边界条件

计算模型的上、下边界施加垂直方向应力，σy=24.0 MPa；左、右边界施加水平方向应力，σx=23.7 MPa。

2.2　模拟结果分析

在隧道开挖后无支护条件下，位移、应力、塑性应变、渗流速度和温度场的模拟结果如图6所示。由图6可得如下结论。

(1)隧道开挖后，隧道边墙处的位移最大，达到749 mm，可见隧道已出现大变形。

(2)拱脚处的围岩应力相对集中，最大值为52.3 MPa，边墙处的围岩应力最小，拱脚和拱顶部位的塑性应变相对较大。

(3)在隧道洞壁处的渗流速度最大，越往围岩内部渗流速度越小，这主要是由于洞壁位于围岩松动圈最外层，围岩位移、塑性应变大，导致渗透率较大，并且洞壁上拱肩至拱脚范围内，渗流速度相对较大，最大值为0.025 8 m·s-1，拱顶和拱底位置的渗流速度相对较小。

(4)左右边墙的温度场分布基本对称，拱顶和隧底温度分布不一致，这主要受地下水热对流控制，与地下水渗流特征具有较好的一致性。

模拟4种不同岩体温度时的围岩最大位移和最大渗流速度，如图7所示。由图7可知：围岩的最大位移和最大渗流速度均与温度呈近似线性增长关系，温度每升高1 ℃，最大位移增大0.980 000 mm，最大渗流速度增大0.000 400 m·s-1。

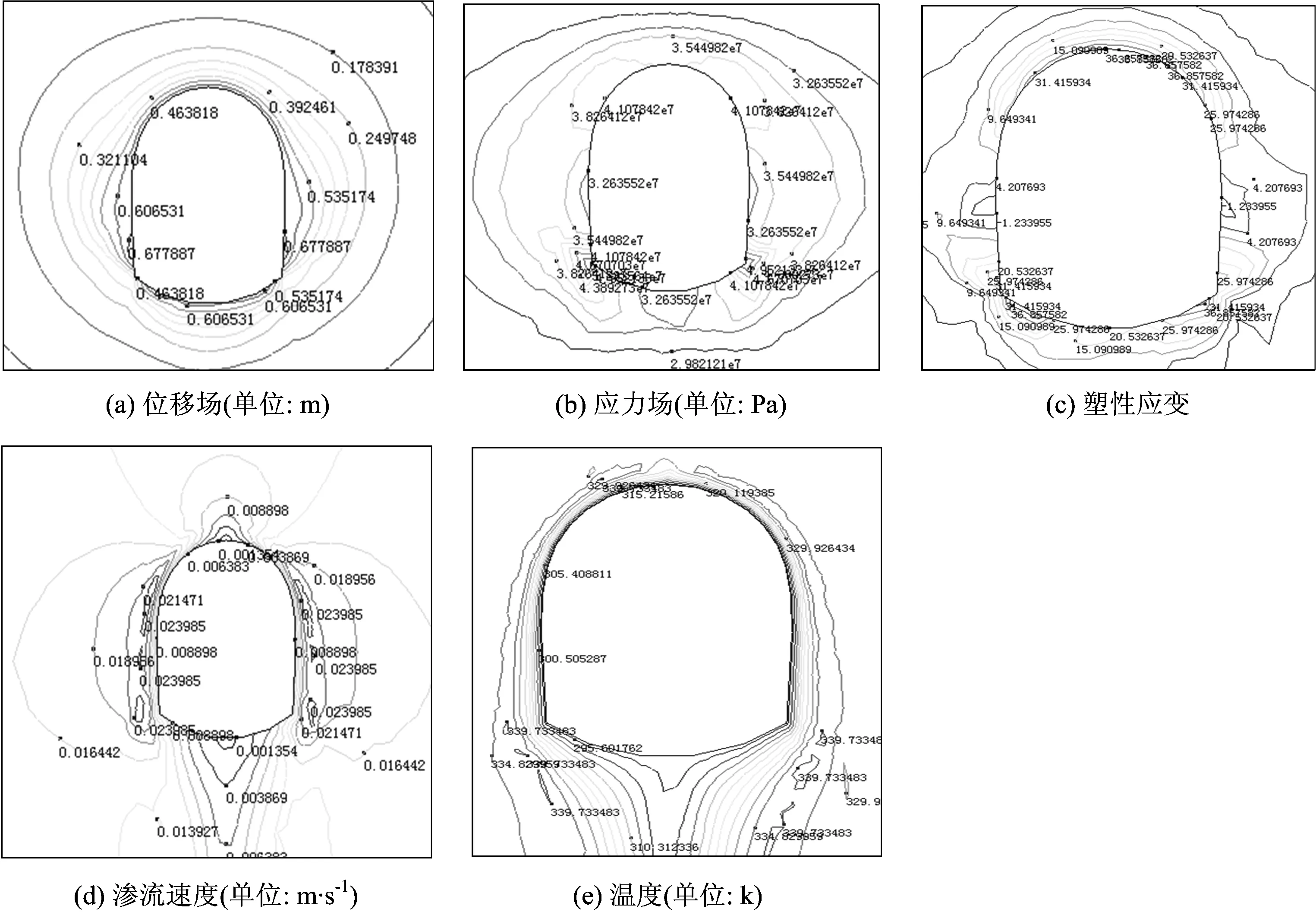
图6　THM耦合模拟结果

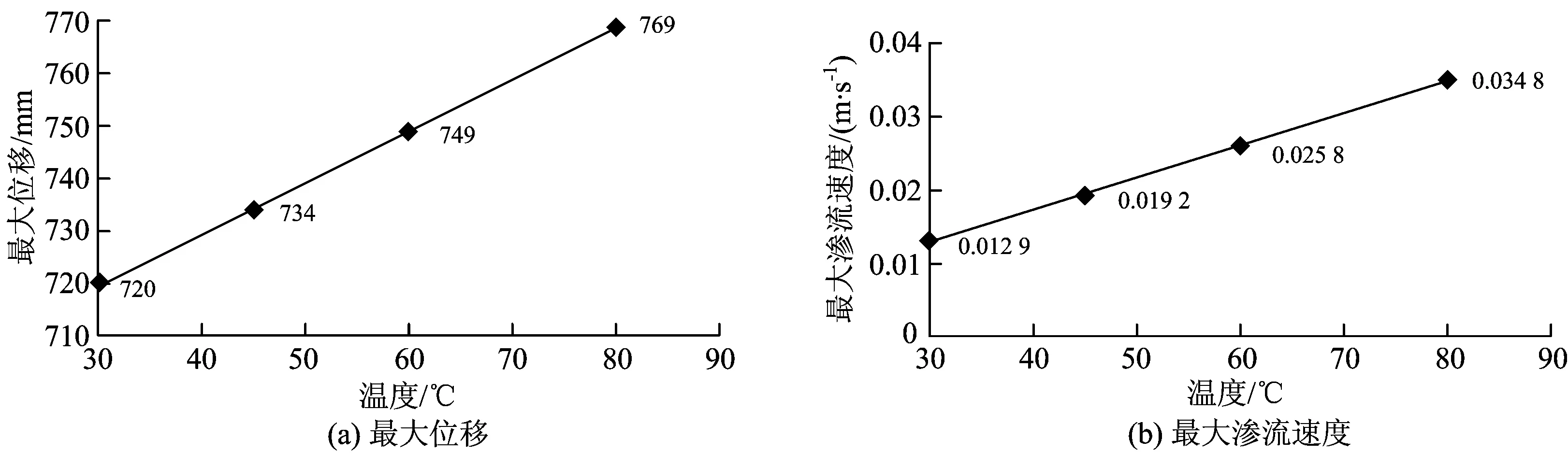
图7　围岩最大位移、最大渗流速度与温度的关系曲线

3　THM耦合作用下隧道大变形机制

综合分析THM耦合作用下室内试验和数值模拟的结果，提出“H↔M，T↔H，T→M”的THM耦合模式，即考虑渗流场与应力场的相互影响(H↔M)、温度场与渗流场的相互影响(T↔H)、温度场对应力场的影响(T→M)，不考虑应力场对温度场的影响，如图8所示。图8中各耦合作用的具体结果如下。

(1)渗流场对应力场的影响(H→M)。表现为渗透水压升高，导致隧道开挖后围岩的应力、位移和塑性应变均增大。

(2)应力场对渗流场的影响(M→H)，表现为围岩应力、位移，塑性应变增大，导致岩体渗透率增大。

(3)渗流场对温度场的影响(H→T)，表现为地下水热对流(渗流方向)，控制着围岩内部温度分布。

(4)温度场对渗流场的影响(T→H)，表现为温度升高，导致隧道开挖后围岩渗流速度增大。

(5)温度场对应力场的影响(T→M)，表现为温度升高，导致隧道开挖后的围岩应力、位移和塑性应变增大。

图8　隧道开挖中的THM耦合模式

应力场是围岩发生大变形的主要因素。对于大多数软弱岩体，隧道开挖卸荷后，破坏了原始地应力场的平衡状态，使一定范围内的围岩应力状态受到了干扰和影响，产生二次应力场重分布。即：洞壁切向应力增大(相当于卸荷试验中轴向应力σ1增大)、径向应力减小(相当于卸荷试验中围压σ3减小)，在洞壁径向应力近乎为零。切向应力的增加和径向应力的降低使应力差增大，从而导致最大剪应力增大，围岩发生卸荷回弹和张剪性破坏，围岩内部出现微裂缝，逐渐向洞内膨胀。当应力重分布达到屈服面后，围岩即处于塑性状态，形成塑性圈，发生塑性流动变形。

渗流场和温度场是围岩发生大变形的重要因素。在“H↔M，T↔H，T→M”耦合作用下，地温和渗透水压对围岩变形破坏特征都有着重要影响，而且两者之间有一定相互关联。渗透水压对围岩内部孔隙和裂纹的挤压扩展，对裂纹的产生和扩张起着促进作用，加之地下水的软化作用，进一步降低了岩体强度，使围岩更易变形。隧道围岩内部温度分布主要受地下水渗流方向控制；洞室围岩温度越高，其自身强度降低，但隧道开挖后的应力、塑性应变、渗流速度越大。由此可见，在隧道开挖过程中，在地温、渗透水压的共同作用下，由于围岩矿物组成差异，高温热膨胀作用使得原本就挤压紧密的围岩在矿物颗粒之间产生新的微裂纹，高渗透水压使得水体进入微裂纹，并对其围岩内部微裂隙的劈裂及裂隙的贯通起着推动作用，围岩更易变形破坏。

综上所述，在THM耦合作用下，在隧道开挖过程中，高地温将造成围岩发生初始热损伤，高渗透水压将促进围岩软化和内部裂纹进一步扩展，隧道开挖形成的二次应力超过围岩屈服强度将导致围岩塑性流动，因此，高地温、高渗透水压和高二次应力是导致千枚岩隧道产生大变形的主要因素。大变形形成示意图如图9所示。

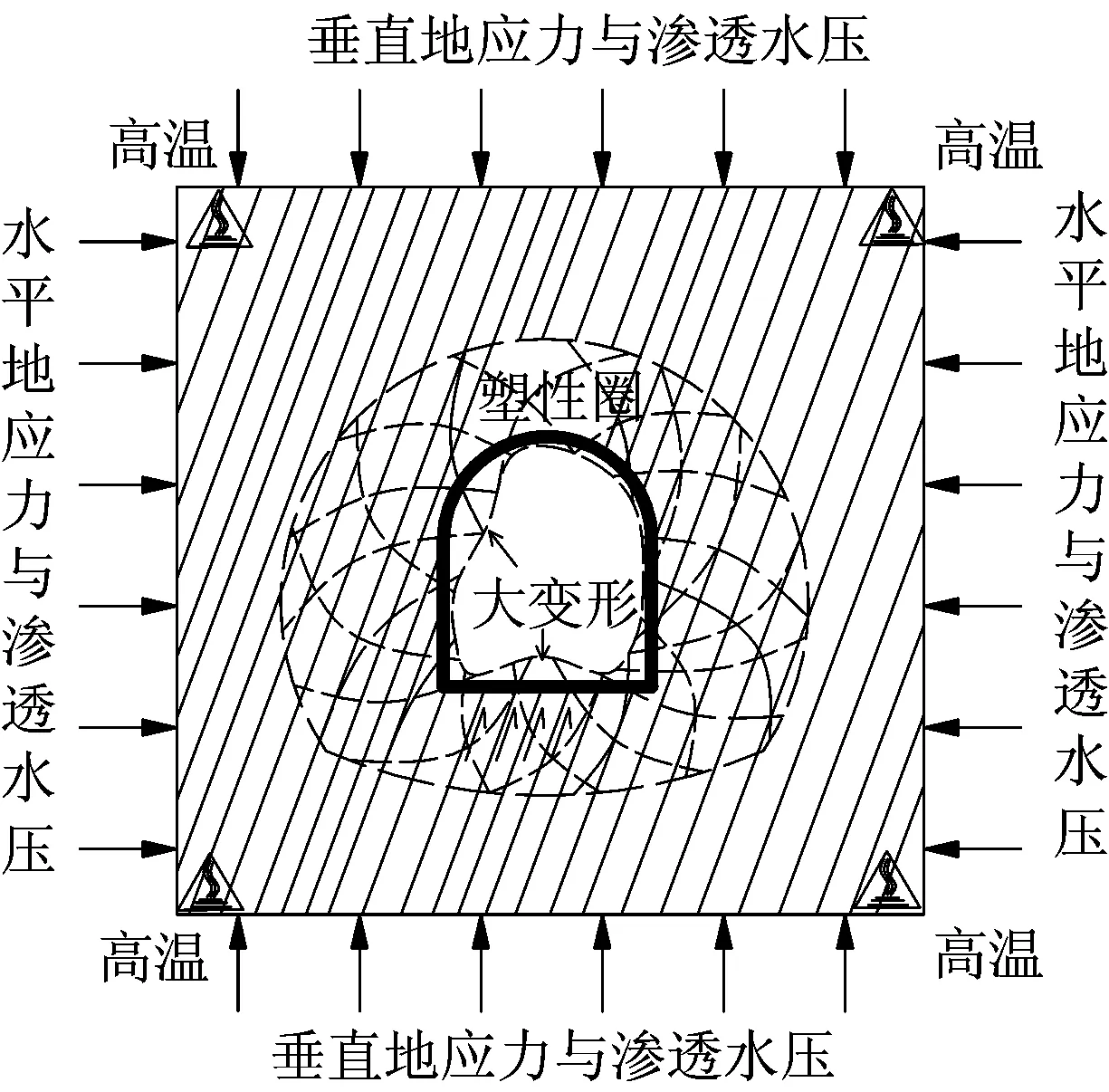
图9　THM耦合作用下隧道大变形形成示意图

4　结　论

(1)高温三轴卸荷渗透模拟试验结果表明：在THM耦合作用下，千枚岩以张剪性破裂为主，膨胀现象明显；高渗透水压和高地温都对千枚岩裂缝的产生和扩张起着促进作用，随着渗透水压、地温的升高，千枚岩的峰值应力降低，并且渗透水压的影响大于地温的影响；岩石渗透率的变化特征与体积应变的发展特征一致，在岩石明显膨胀后，渗透率急剧增大。

(2)二维数值模拟结果表明：在THM耦合作用下，隧道边墙处的位移最大，拱脚处的应力相对集中，洞壁处的渗流速度最大，左右边墙的温度场分布基本对称，拱顶和隧底的温度分布不一致；隧道围岩内部的温度分布主要受地下水渗流方向控制；隧道洞壁的应力、位移和渗流速度随围岩温度的升高而增大。

(3)提出了“H↔M、T↔H、T→M”的THM耦合模式，即考虑渗流场与应力场的相互影响(H↔M)、温度场与渗流场的相互影响(T↔H)、温度场对应力场的影响(T→M)，不考虑应力场对温度场的影响。

(4)在THM耦合作用下千枚岩隧道产生大变形的机理为：高地温将造成围岩发生初始热损伤，高渗透水压将促进围岩软化和内部裂纹进一步扩展，隧道开挖形成的二次应力超过围岩屈服强度后将导致围岩塑性流动。

[1]BROX D, HAGEDORN H. Extreme Deformation and Damage during the Construction of Large Tunnels [J]. Tunnelling and Underground Space Technology, 1999，14(1): 23-28.

[2]MENG Lubo, LI Tianbin, JIANG Yun, et al. Characteristics and Mechanisms of Large Deformation in the Zhegu Mountain Tunnel on the Sichuan-Tibet Highway[J]. Tunnelling and Underground Space Technology, 2013, 37:157-164.

[3]王树英,阳军生,李习平. 高地应力凝灰岩地层铁路隧道支护结构大变形的原因及其整治[J]. 中国铁道科学, 2014,35(5):47-54.

(WANG Shuying, YANG Junsheng, LI Xiping. Causes and Renovation for Large Deformation in Supporting Structure of Railway Tunnel in Tuff Formation under High Geostress[J]. China Railway Science, 2014,35(5):47-54. in Chinese)

[4]刘高,张帆宇,李新召，等. 木寨岭隧道大变形特征及机理分析[J].岩石力学与工程学报,2005, 24(增2)：5521-5526.

(LIU Gao, ZHANG Fanyu, LI Xinzhao, et al. Research on Large Deformation and Its Mechanism of Muzhailing Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering，2005, 24 (Supplement 2): 5521-5526. in Chinese)

[5]王树栋，刘开云. 长大隧道软弱围岩施工大变形智能预测方法[J]. 中国铁道科学,2008,29(2):82-87.

(WANG Shudong, LIU Kaiyun. Intelligence Method for Large Deformation Prediction of Weak Surrounding Rock Construction in Long and Large Tunnel[J]. China Railway Science, 2008, 29(2):82-87. in Chinese)

[6]李鹏飞,赵勇,刘建友. 隧道软弱围岩变形特征与控制方法[J]. 中国铁道科学,2014,35(5):55-61.

(LI Pengfei, ZHAO Yong, LIU Jianyou. Deformation Characteristics and Control Method of Tunnel with Weak Surrounding Rock[J]. China Railway Science, 2014, 35(5):55-61. in Chinese)

[7]汪波,李天斌,何川,等. 强震区软岩隧道大变形破坏特征及其成因机制分析[J]. 岩石力学与工程学报,2012,31(5):928-936.

(WANG Bo, LI Tianbin, HE Chuan, et al. Analysis of Failure Properties and Formatting Mechanism of Soft Rock Tunnel in Meizoseismal Areas[J]. Chinese Journal of Rock Mechanics and Engineering. 2012, 31(5):928-936. in Chinese)

[8]EINSTEIN H H. Tunneling in Swelling Rock[J]. Underground Space, 1979,4(1):51-61.

[9]ANAGNOSTOU G. A Model for Swelling Rock in Tunneling[J]. Rock Mechanics and Rock Engineering, 1993,26(4):307-331.

[10]张颖钧,王小军. 云台山隧道膨胀岩的膨胀特性[J]. 中国铁道科学,1994,15(2):96-106.

(ZHANG Yinjun, WANG Xiaojun. Expansive Properties of the Rock Strata in Yun Taishan Tunnel[J]. China Railway Science,1994,15(2):96-106. in Chinese)

[11]王小军. 膨胀岩的判别与分类和隧道工程[J]. 中国铁道科学,1994,15(4):79-86.

(WANG Xiaojun. The Discrimination and Classification of Swelling Rocks in Tunnel Engineering[J]. China Railway Science, 1994,15(4):79-86. in Chinese)

[12]戴永浩,陈卫忠,于洪丹,等.大坂膨胀性泥岩引水隧洞长期稳定性分析[J].岩石力学与工程学报,2010, 29(增1):3227-3234.

(DAI Yonghao, CHEN Weizhong, YU Hongdan, et al. Long-Term Stability Analysis of Daban Diversion Tunnel Buried in Swelling Mudstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Supplement 1):3227-3234. in Chinese)

[13]陈宗基.地下巷道长期稳定性的力学问题[J].岩石力学与工程学报, 1982，1(1):1-19.

(CHEN Zongji. The Mechanical Problems for Long-Term Stability of Underground Galleries[J]. Chinese Journal of Rock Mechanics and Engineering， 1982， 1(1):1-19. in Chinese)

[14]AYDAN O, AKAGI T, KAWAMOTO T. The Squeezing Potential of Rocks around Tunnels: Theory and Prediction[J]. Rock Mechanics and Rock Engineering，1993,26(2):137-163.

[15]姜云,李永林,李天斌,等. 隧道工程围岩大变形类型与机制研究[J]. 地质灾害与环境保护,2004,15(4):46-51.

(JIANG Yun, LI Yonglin, LI Tianbin, et al. Study of the Classified System of Types and Mechanism of Great Distortion in Tunnel and Underground Engineering[J]. Journal of Geological Hazards and Environment Preservation, 2004, 15(4): 46-51. in Chinese)

[16]中华人民共和国水利部. SL264—2001水利水电工程岩石试验规程[S].北京:中国水利水电出版社,2001.

(The Ministry of Water Resources of the People’s Republic of China. SL264—2001 Specifications for Rock Tests in Water Conservancy and Hydroelectric Engineering[S]. Beijing：China Water & Power Press，2001. in Chinese)

[17]杨立中,黄涛,贺玉龙.裂隙岩体渗流—应力—温度耦合作用的理论与应用[M].成都:西南交通大学出版社,2008.