基于典型壁面粗糙模型的隧道施工通风效果CFD分析

张　恒，林　放，孙建春，周泽林

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都　610031)

目前长大隧道施工通常以钻爆法并结合无轨运输为主，施工期间通风问题成为首要面临的一个难题，如何将污风顺利排出成为隧道快速施工的关键所在。其中隧道洞壁粗糙度对实际通风效果具有一定的影响，但TB 10068—2010《铁路隧道运营通风设计规范》中以隧道内平均壁面粗糙度及隧道断面当量直径作为通风设计的主要考虑因素，一些研究中以此计算通道内沿程阻力系数[1-5]，因此计算结果与实际情况有偏差。还有的一些研究成果中，在采用计算流体动力学(Computational Fluid Dynamics，CFD)模拟隧道施工中的通风过程时，将洞壁视为光滑壁面，几乎不考虑洞壁粗糙情况对通风效果的影响，因此模拟结果与实际通风效果并不完全一致[6-8]。当风流通过凹凸不平的壁面时，其风流场是复杂多变的，用数学推导的方式对这种条件下流体的阻力进行研究难以实现[9-11]。因此，本文基于贵广高速铁路斗篷山隧道采用钻爆法施工的通风工程，采用CFD软件，结合现场实测，研究隧道壁面粗糙条件对风流的影响，并深入分析壁面粗糙度的评定方法、取值以及工程应用，以为隧道施工通风设计提供理论支持。

1　CFD软件中壁面粗糙度的定义

流体在流动过程中的流动阻力、传热和传质都会受到壁面粗糙度的影响。现有的CFD软件中用于定义壁面粗糙度的一般有2个参数：粗糙高度(Roughness Height，用Rh表示)和粗糙常数(Roughness Constant，用Rc表示)。并且规定：当壁面是光滑平面时，Rh的值为0；当壁面是均匀分布的粗糙颗粒时，Rh的值为颗粒的高度；当壁面是非均匀分布的粗糙颗粒时，Rh的值为颗粒的平均高度；对于其他类型的粗糙颗粒，可以按照“等价”的方式进行处理。粗糙度常数Rc是与粗糙颗粒类型密切相关的1个参数，软件中默认Rc的初始值等于0.5，即采用Rc初始值能够准确计算均匀颗粒的粗糙度。如果壁面粗糙颗粒的类型与均匀粗糙颗粒相差较大时，通过调整Rh的值可以避免计算结果出现较大偏差。例如壁面条件是非均匀的沙粒或者是肋板等，Rc的取值范围应在0.5～1.0之间。但是，目前在CFD软件中，对于任意形状的粗糙颗粒，还没有1个关于Rc取值的通用准则，即没有提供对应不同粗糙颗粒材料类型的Rc合理取值范围。

2　典型壁面对流体流通的影响

2.1　典型壁面粗糙模型

在实际工程中，壁面上存在形状不同、大小不一，且错落分布的突起物时，即壁面为凹凸不平时，则壁面存在一定的粗糙度，将这些凹凸单元称为粗糙单元。当流体以较小的流速通过这些粗糙单元附近时，壁面附近的流线基本上平行于粗糙单元的外轮廓。当流体的流速增大到一定值后，受粗糙单元形状和尺寸的影响，即受粗糙单元前后产生的形状阻力[12-14]的影响，流体在粗糙单元背后会出现一定程度的流体脱离和再附着以及回流过程，从而导致流体流动的阻力增大。可见，流体在粗糙壁面附近的流线是复杂多变的。

为了确保所得研究结果具有普遍性，分析过程中选取4种典型壁面粗糙模型，分别是正弦型粗糙模型、方形粗糙模型、三角形粗糙模型、矩形与三角形交替间隔粗糙模型，如图1所示，图中2L为波长。

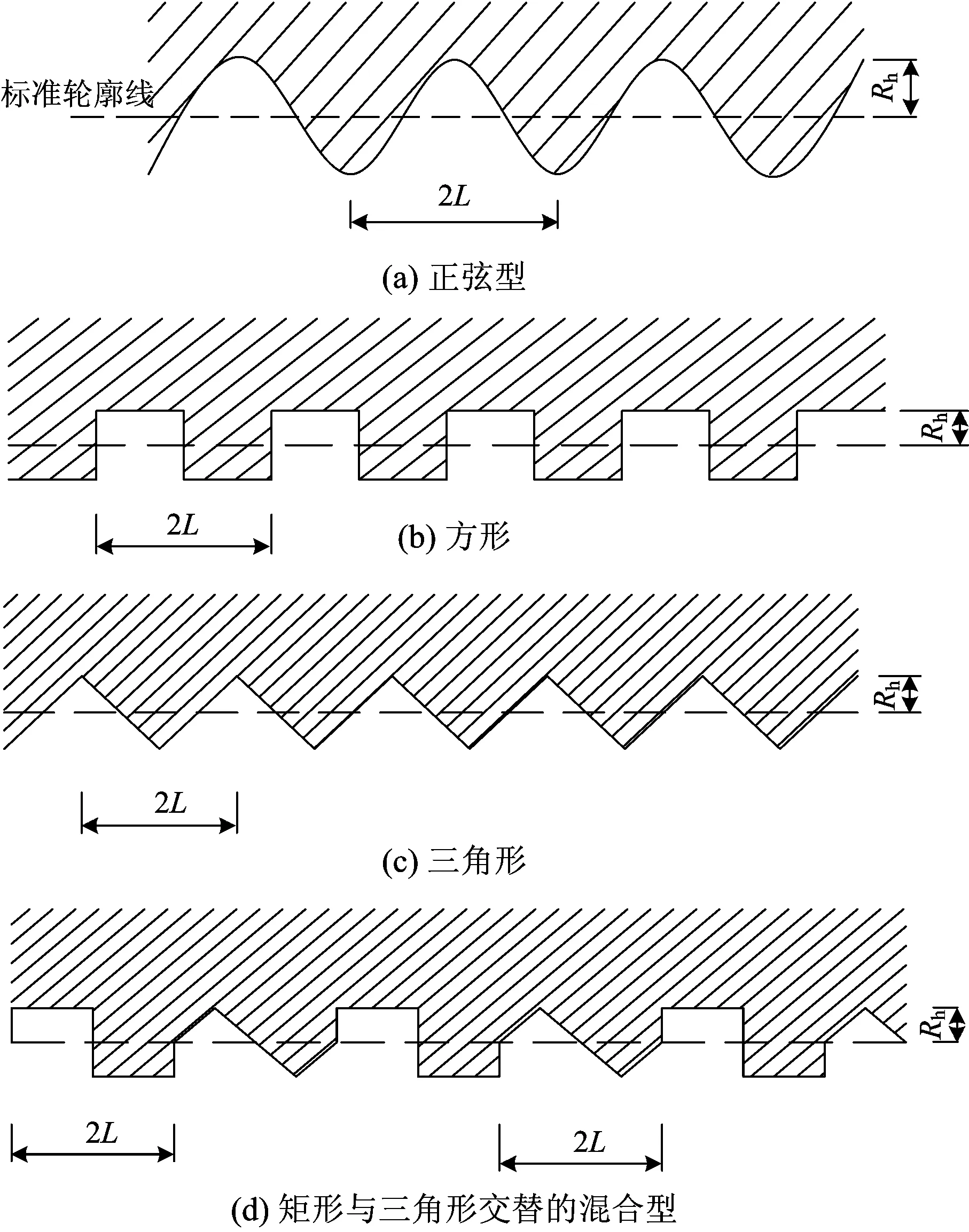
图1　4种典型的壁面粗糙模型

2.2　数值计算参数及边界条件

依托贵广高速铁路斗篷山隧道施工通风工程进行研究。斗篷山隧道全长7 369 m，设计为双线单洞隧道，最大埋深470 m，开挖跨度13 m，采用钻爆法施工。隧道分进口、出口、斜井3个作业区，4个工作面，考虑到实际的工作情况及经济因素，斗篷山隧道进、出口及斜井均采用压入式通风，各配置1台110 kW×2的轴流风机向工作面送风，风管为焊接式、双拉链接头1.5 m软式通风管。

隧道断面直径为13 m，取隧道纵向长度100 m建立数值模型，如图2所示，研究通风排烟过程中CO气体排出受隧道壁面粗糙条件影响的程度。根据现场施工爆破作业炸药用量和隧道断面尺寸，计算出爆破后炮烟的抛掷长度及掌子面附近初始污染区的范围，如图2所示。选取典型壁面模型凹处最低点的连线建立1条计算监测界线，如图3所示。

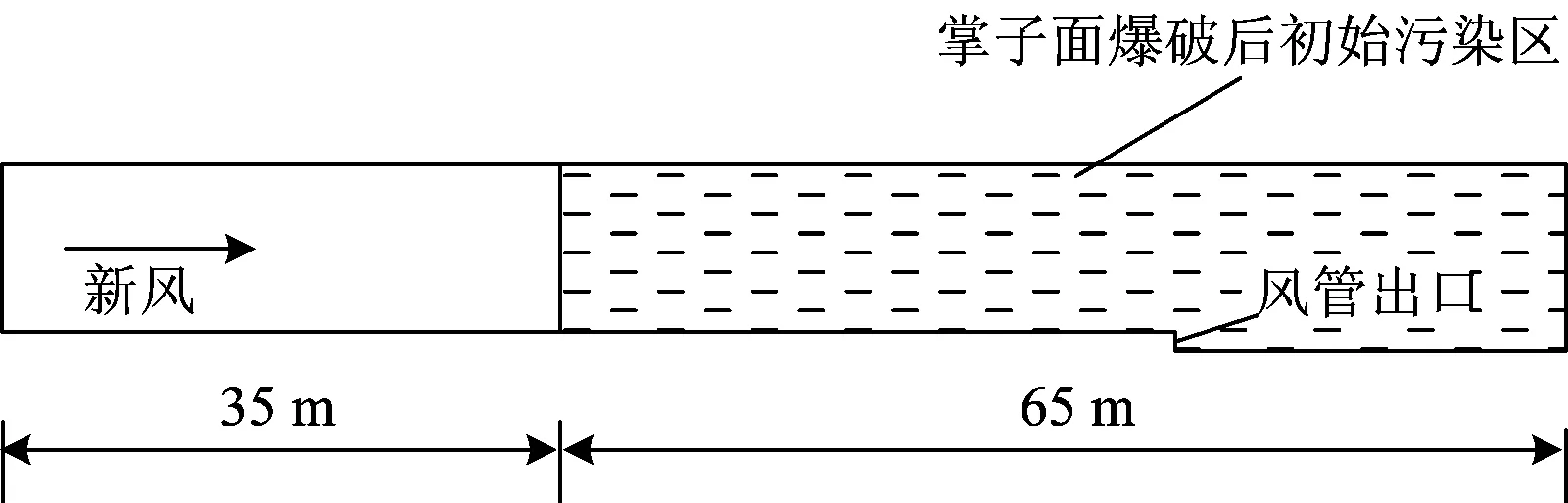
图2　数值模型尺寸及初始污染区的范围

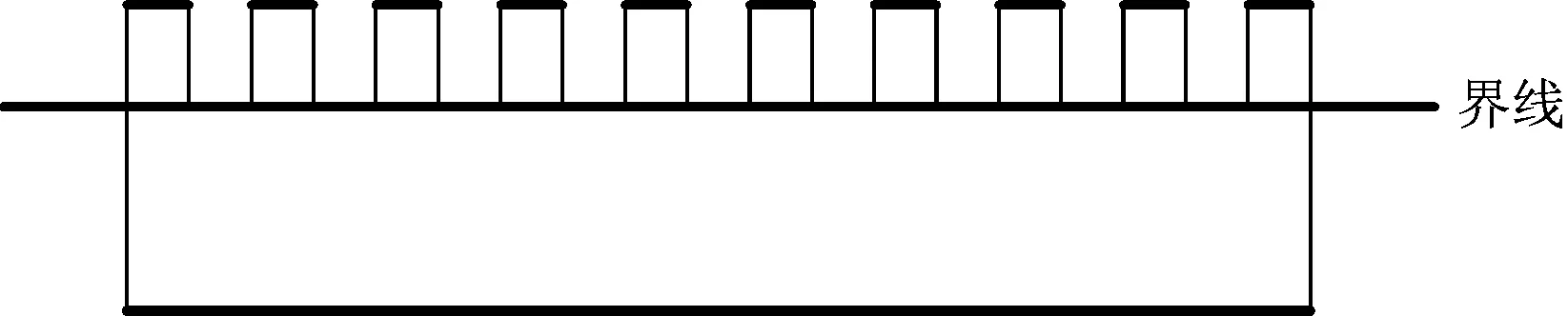
图3　粗糙模型的计算监测界线示意图

将隧洞内的空气流动看做是三维不可压缩稳定的黏性紊流，紊流流动的模型采用高雷诺数k-ε模型。压入式的风管为直径1.5 m的螺旋焊接风管，管口出风速度为12.5 m·s-1。隧道进风口设为速度入口边界，隧道出风口设为CFD软件中的outflow边界，风机出风口设为等速边界。

2.3　数值计算结果分析

2.3.1粗糙形状对风流场的影响

4种典型壁面粗糙模型的壁面线条各自作周期性重复，固定其波长均为2L，粗糙高度均为Rh。取波长2L=2 m，粗糙高度Rh=0.5 m，通风时间为5 min。分别采用4种典型壁面粗糙模型时近壁区域的速度矢量分布如图4所示。由图4可知：仅正弦型粗糙模型在近壁区域没有产生涡流现象，其他3种粗糙模型都存在不同程度的涡流，这是因为正弦型粗糙模型的壁面条件相比方形、三角形和混合型更为光滑；在远离粗糙近壁的隧道内部区域，4种模型的速度分布均较为均匀；因此，正弦型粗糙模型对风流场起到的阻碍作用相对较小。

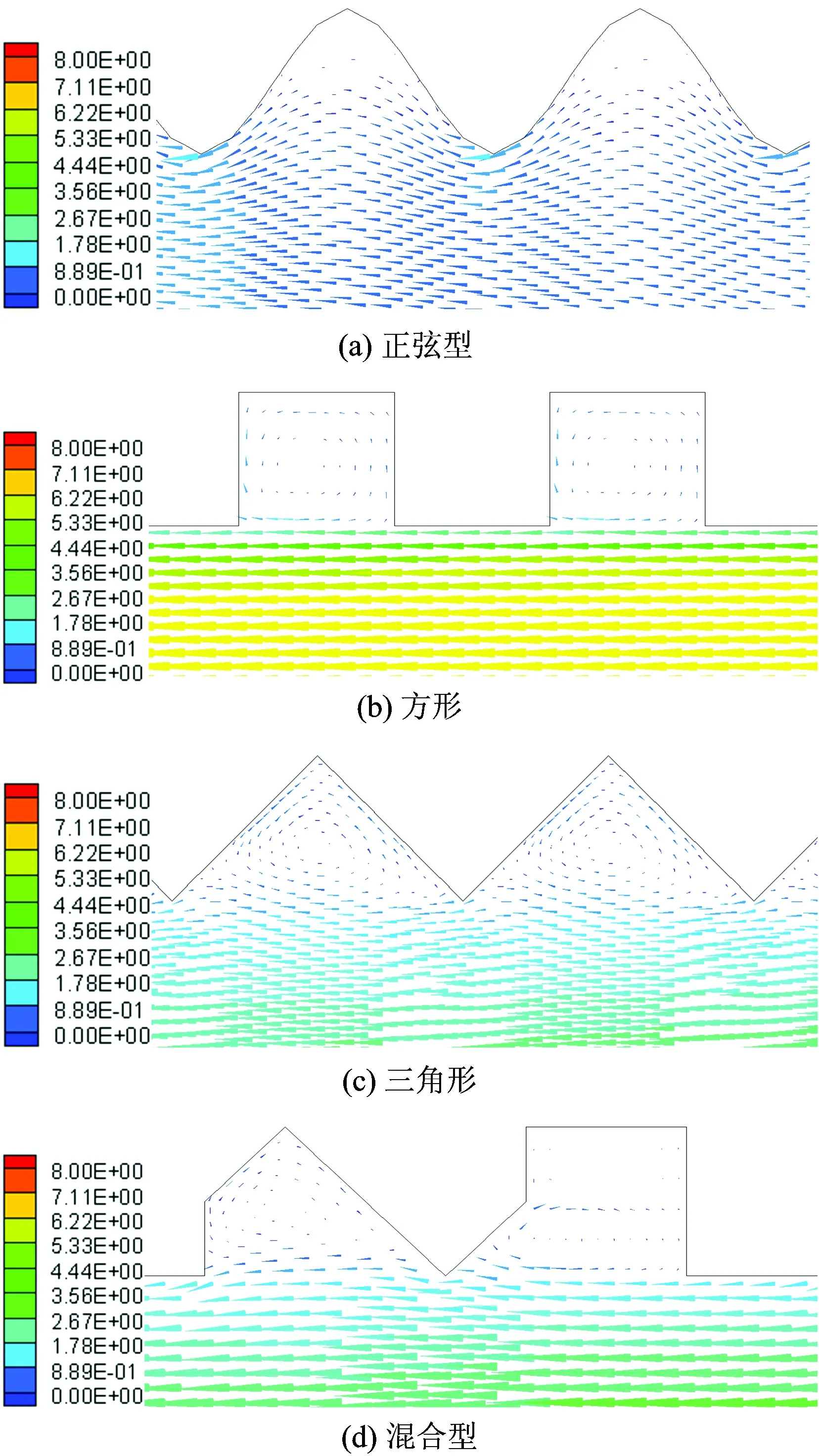
图44种典型壁面粗糙模型的速度矢量分布局部放大图(单位：m·s-1)

2.3.2粗糙高度对风流场的影响

为了研究典型壁面粗糙模型的高度、间距以及同一粗糙条件下隧道断面直径对风流场的影响，选取正弦型粗糙模型为例进行说明。粗糙高度分别取Rh=0.1，0.3，0.5，0.7，1.0 m，波长2L=2 m，通风5 min后正弦型粗糙模型在5种粗糙高度下隧道内CO浓度(体积比)的分布(通风效果)如图5所示。由图5可知：随着粗糙高度的增大，壁面条件对风流场的阻碍作用越大，越不利于隧道内CO的排出，造成在隧道内特别是近粗糙壁面附近CO浓度增大。

2.3.3粗糙间距对风流场影响

粗糙间距(即为正弦曲线波长)分别取2L=0.5，1.0，2.0，3.0，4.0，5.0 m，Rh=0.5 m，通风5 min后正弦型粗糙模型在6种粗糙间距下隧道内CO浓度的分布(通风效果)如图6所示。由图6可知：随着粗糙间距的增大，壁面条件对风流场的阻碍作用越小，越有利于隧道内CO的排出。

图5　5种粗糙高度下隧道内CO浓度的分布

2.3.4计算监测界线上CO浓度的分布

与掌子面间的距离均分别取10，20，…，100 m，在光滑模型和4种典型粗糙模型条件下，通风5 min后计算监测界线上的CO浓度分布如图7所示。Rh=0.1，0.3，0.5，0.7，1.0 m，波长2L=2 m，在正弦型粗糙模型条件下，通风5 min后计算监测界线上CO浓度的分布如图8所示。2L=0.5，1.0，2.0，3.0，4.0，5.0 m，Rh=0.5 m，在正弦型粗糙模型条件下，通风5 min后计算监测界线上CO浓度的分布如图9所示。分别对比图4与图7，图5与图8，图6与图9可知：计算监测界线上的CO浓度分布规律与隧道内的分布规律一致；隧道壁面越粗糙，对隧道内流体起到的阻碍作用越大，CO污染物越难快速排出洞外。由图8、图9可以看出：粗糙高度对风流场的影响比粗糙间距的影响要大。

2.3.5通风5 min后CO在隧道内的分布规律

采用正弦型粗糙模型，波长2L=2 m，粗糙高度Rh=0.5 m，通风5 min后隧道内CO浓度的云图如图10所示。由图10可知：工作面附近涡流中心处的CO浓度最高。这是由于：工作面附近涡流区内的气体流动速度小，流线封闭，导致CO浓度不能及时扩散，同时部分CO又随风回流至工作面，由此导致涡流中心处CO 浓度最高；涡流对扩散有明显的滞留作用，导致涡流中心有害气体浓度高。

图6　6种粗糙间距下隧道内CO浓度的分布

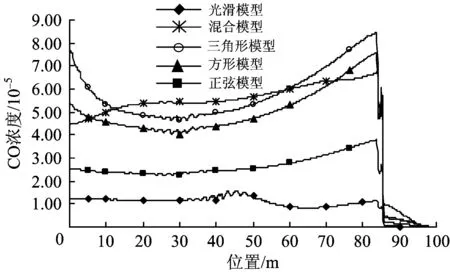
图7　5种粗糙模型下计算监测界线上CO浓度的分布

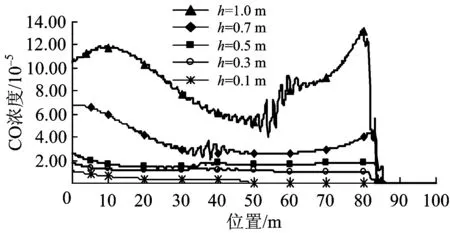
图8正弦型粗糙模型下不同粗糙高度时计算监测界线上CO浓度的分布

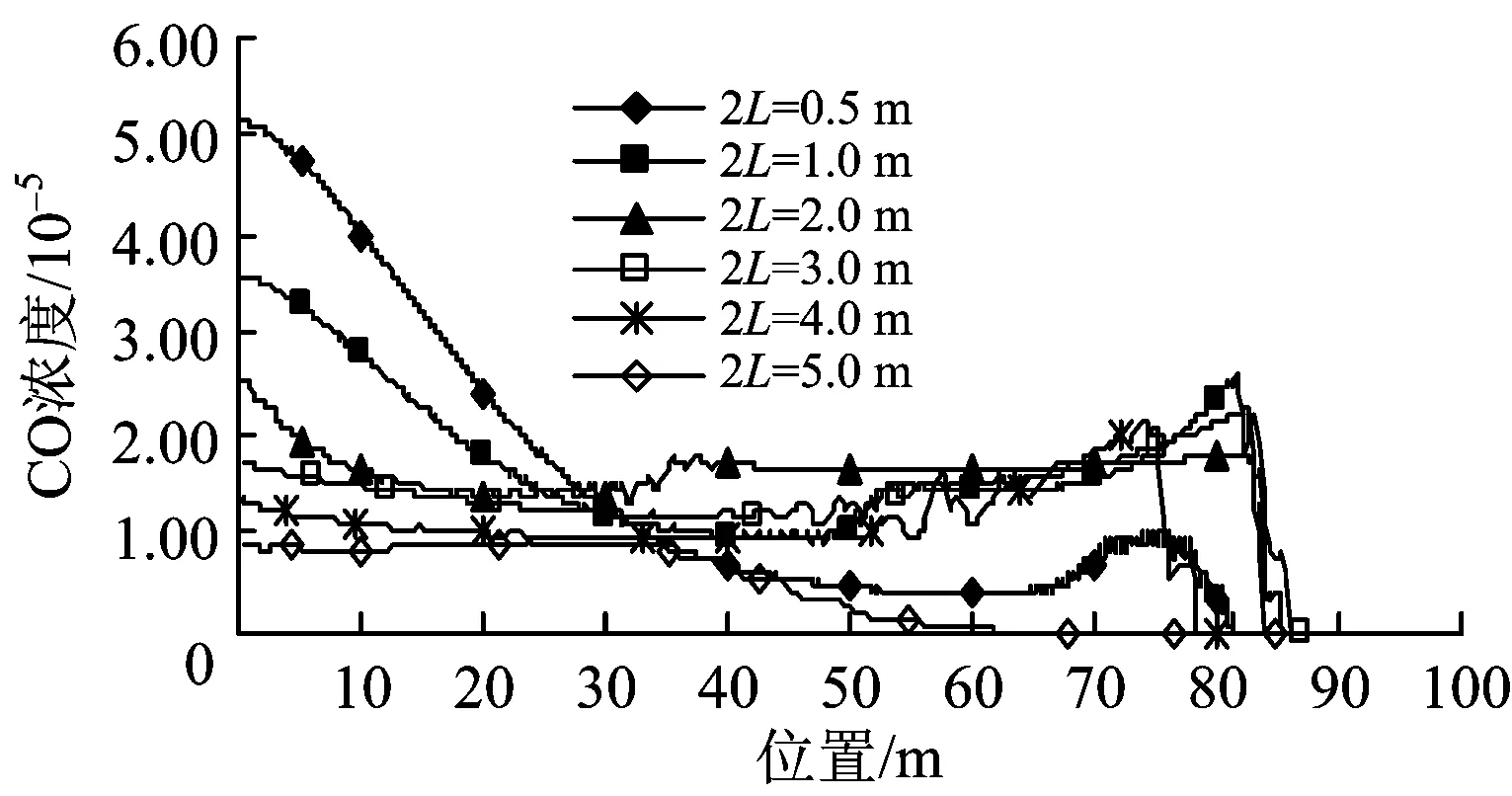
图9正弦型粗糙模型下不同波长时计算监测界线上CO浓度的分布

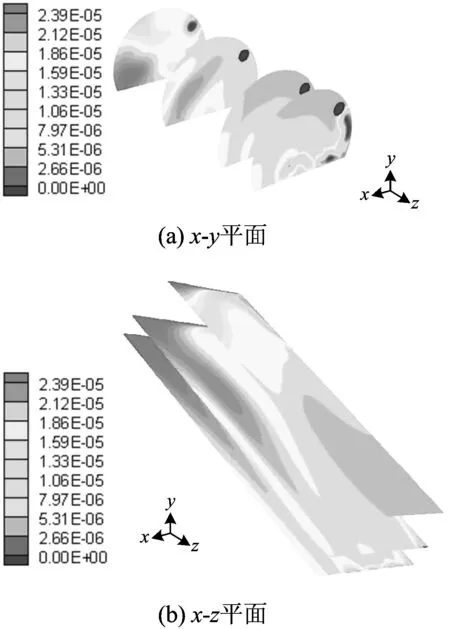
图10　隧道内CO浓度的云图

3　粗糙高度计算方法及粗糙常数取值

3.1　粗糙高度的计算方法

在实际工程中，隧道采用钻爆法施工，开挖轮廓(隧道壁面)不可避免地会是凹凸不平的不规则的几何形状，如图11所示，图中Rh为壁面的平均粗糙高度。为了限制和减弱其他几何形状误差对壁面粗糙度量测结果的影响，在测量和评定隧道壁面粗糙度时规定一段基准长度，称为取样长度M(见图11)，实际工程中一般沿隧道轴向选取取样长度M=10 m。

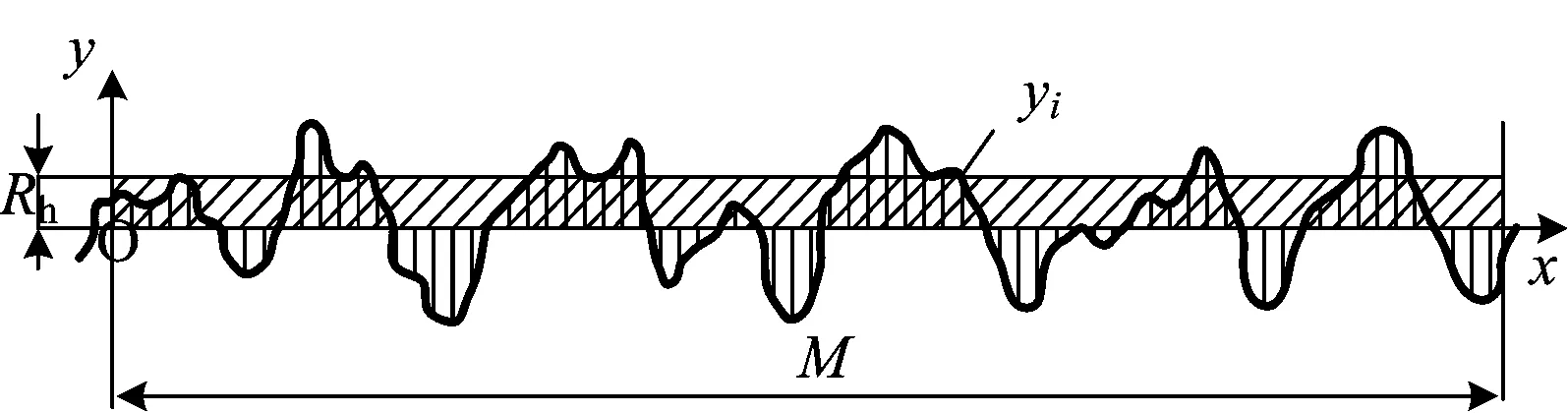
图11　隧道开挖时不规则轮廓线与设计轮廓线包络图

Rh的具体计算方法是：在取样长度内，以实际开挖轮廓上的点与基准线(设计开挖轮廓线)之间距离绝对值的算术平均值作为Rh值，即

(1)

式中：n为分割点的总数；yi为取样长度内实际开挖轮廓线上第i段轮廓线至基准线的距离；y为取样长度内实际开挖轮廓线至基准线的距离；dx为第i段的长度。

由图11和式(1)可知：Rh的值等于隧道实际开挖轮廓线和设计开挖轮廓线两者包络的面积与基准长度的比值。

3.2　粗糙常数的计算方法

由于CFD软件中粗糙常数Rc是一个与粗糙形状、粗糙间距相关的参数，因此需要建立粗糙形状、间距与Rc值的对应关系。具体实现步骤为：第1步，在相同的平均粗糙高度Rh前提下，固定模型的粗糙形状和间距，在一定的计算时间步下，得到整个隧道内部的速度矢量分布场及CO浓度分布场；第2步，通过调整计算软件中Rc的取值，使得在同样的计算时间步下，计算所得到的速度矢量分布场及CO浓度分布场与前一步骤所得结果一致。

以Rh=0.3 m，2L=2 m，正弦粗糙模型为例，说明获得合适Rc值的方法。首先，参考图11及式(1)可以得到该正弦型粗糙模型的平均粗糙高度，计算得到的平均粗糙高度Rh=0.17 m(该值即为软件输入的Rh)；在Rc=0.47条件下，计算120个时间步，所得到的流体速度及CO浓度分布场与Rh=0.3 m，2L=2 m的正弦粗糙单元模型在同样时间步下获得的流体速度及CO浓度的大小和分布大致一致，这样基本可以认为CFD软件中Rh=0.17，Rc=0.47时，所对应的是Rh=0.3 m，2L=2 m的正弦粗糙模型，如图12和图13所示。

分别采用三角形、方形和正弦型粗糙模型按照上述方法进行计算，得到不同粗糙间距下的Rc值，如图14所示。对图14中Rc值采用多项式拟合、一阶指数衰减拟合及线性拟合3种方式进行数据处理分析，其结果分别见图14中的y1，y2，y3。由图14可以看出，采用一阶指数衰减拟合方式得到的拟合结果与计算结果吻合较好。

图12　　　　通风计算120个时间步时流体速度分布云图(单位：m·s-1)

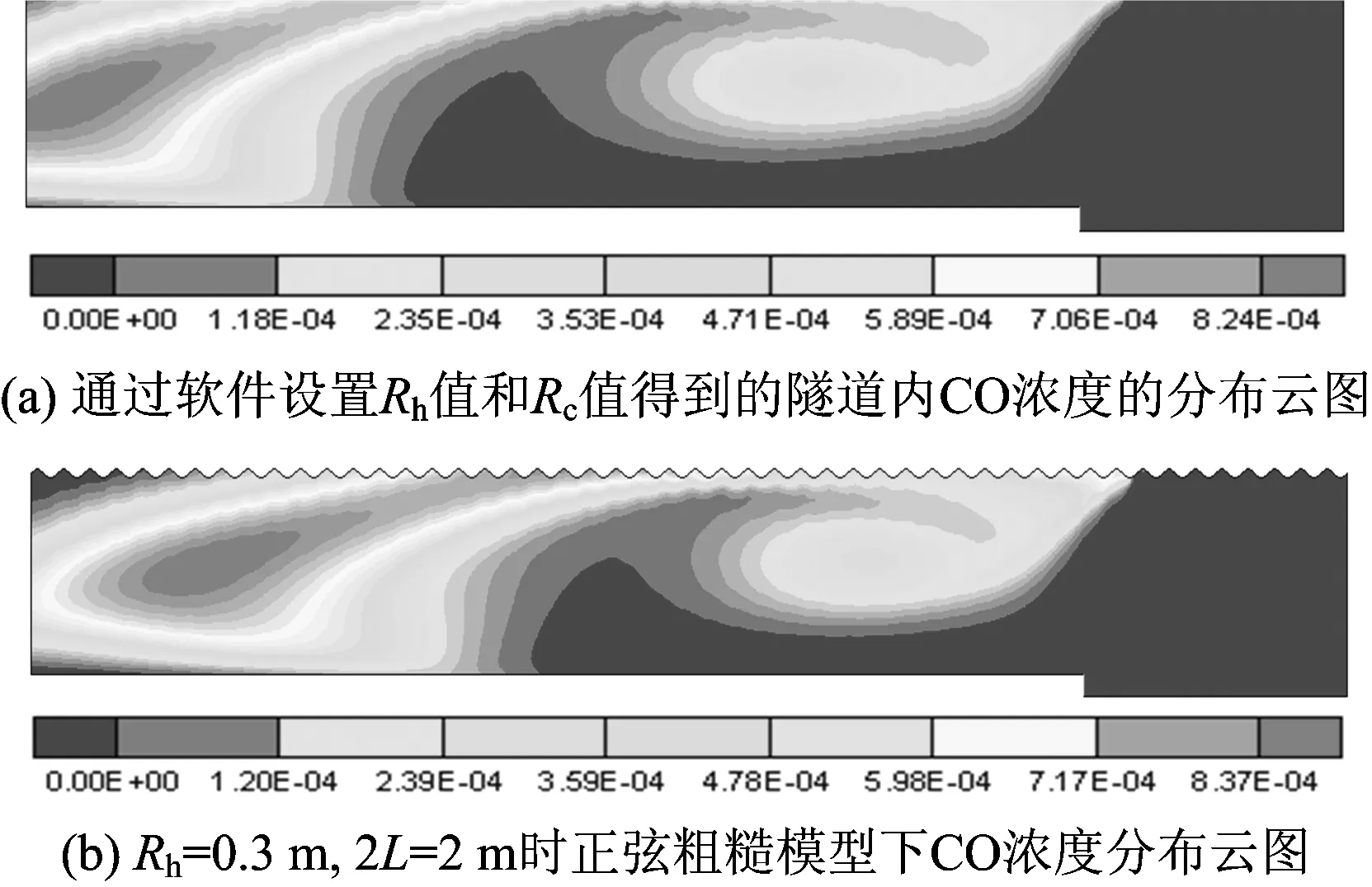
图13　通风计算120个时间步时隧道内CO浓度的分布云图

3.3　基于最优简化模型粗糙常数Rc的计算方法

由于图14中粗糙常数Rc与粗糙模型的对应关系是以典型壁面粗糙模型为前提建立的，而实际工程中隧道壁面为不规则的几何形状，因此，计算时应先将实际开挖断面的不规则轮廓线简化为图1中的1种或几种组合的典型粗糙模型，即简化为最优简化模型。

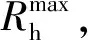
(2)

式中：S原为原实际开挖轮廓线包络的面积；S三角形为三角形模型包络的面积；S方形为方形模型包络的面积，S正弦为正弦形模型包络的面积。

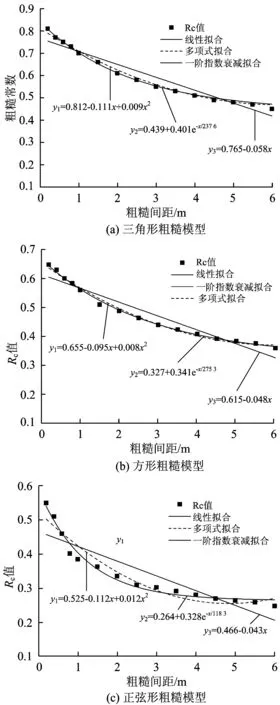
图14　3种粗糙模型的不同粗糙间距下计算的粗糙常数Rc

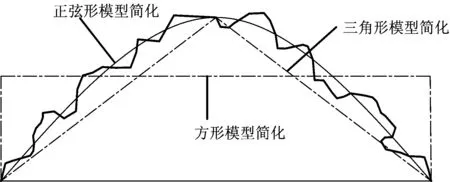
图15　粗糙模型的简化

图16所示为1条取样长度为M的不规则开挖轮廓线。根据实测取样长度内壁面的凹凸情况分为X1,X2,…,X8共8小段；将每1个小段按照图15及式(2)的简化方法进行简化，最后得到图17所示的最优简化模型。

图16　实测取样长度为M的不规则开挖轮廓线

图17　取样长度为M的开挖轮廓线的最优简化模型

根据每段对应的典型粗糙模型，计算对应的Rc1，Rc2，…，Rc8；根据式(3)则可近似计算得到隧道开挖面为不规则轮廓线时的Rc。

(3)

4　结　论

(1)由于正弦形粗糙模型的壁面条件相比方形、三角形和混合型更为光滑，因此该模型对风流场起到的阻碍作用相对较小，近壁区域没有产生涡流现象。

(2)在相同的隧道断面直径下，随着粗糙高度的增大、粗糙间距的减小，壁面条件对风流场的阻碍作用越大，越不利于CO的排出。

(3)将隧道实际开挖轮廓上的点与基准线(设计开挖轮廓线)之间距离绝对值的算术平均值定义为平均粗糙高度，并建立了粗糙常数Rc与粗糙模型的形状及间距的对应关系。

(4)基于典型壁面粗糙模型，以典型壁面粗糙模型的最大粗糙高度Rh不大于实际开挖轮廓的最大粗糙高度，且原模型面积减去典型模型面积的绝对值除以原模型面积所得值最小为最优简化模型，提出了壁面粗糙常数的近似计算公式。

[1]张恒. 复杂网络隧洞群施工通风技术研究[D]. 成都：西南交通大学, 2013.

(ZHANG Heng. Construction Ventilation Technology of Complex Network Tunnel Group[D]. Chengdu: Southwest Jiaotong University, 2013. in Chinese)

[2]王磊, 郭洋洋. 特长公路隧道运营网络通风技术[J]. 长安大学学报：自然科学版, 2012, 32(4): 51-54.

(WANG Lei, GUO Yangyang. Network Ventilation Technology of Operation Period in Super Long Highway Tunnel[J]. Journal of Chang’an University: Natural Science Edition, 2012, 32(4): 51-54. in Chinese)

[3]王晓玲, 刘震, 杨安林, 等. 考虑热交换的引水隧洞施工通风两相流模拟[J]. 天津大学学报: 自然科学与工程技术版, 2013, 46(4):322-327.

(WANG Xiaoling, LIU Zhen, YANG Anlin, et al. Simulation for Construction Ventilation Two-Phase Flow in Diversion Tunnel Considering Heat Exchange[J]. Journal of Tianjin University: Science and Technology, 2013, 46(4):322-327. in Chinese)

[4]何坤, 叶敏敏, 李艳玲, 等. 交叉隧洞施工通风流场特性研究[J]. 四川大学学报: 工程科学版, 2014, 46(增刊1):20-25.

(HE Kun, YE Minmin, LI Yanling,et al.Characteristic Research on Construction Ventilation Flow Field of Cross Tunnel[J]. Journal of Sichuan University: Engineering Science Edition, 2014, 46(Supplement 1):20-25. in Chinese)

[5]HERWIG H, GLOSS D, WENTERODT T. 粗糙壁面通道内的流动研究[J]. 中国计量学院学报, 2008, 19(4): 296-303.

(HERWIG H, GLOSS D, WENTERODT T. Flow in Channels with Rough Walls—Old and New Concepts[J]. Journal of China Jiliang University, 2008, 19(4): 296-303. in Chinese)

[6]纪杰, 钟委, 张英, 等. 典型多层地铁车站中间层起火时的通风模式优化分析[J]. 中国铁道科学, 2010, 31(2):131-136.

(JI Jie, ZHONG Wei, ZHANG Ying, et al. Optimization of Ventilation Mode during Intermediate-Floor Fire in a Typical Multi-Floor Subway Station[J]. China Railway Science, 2010, 31(2):131-136. in Chinese)

[7]谢宁, 冯炼, 王婉娣, 等. 隧道火灾三维数值模拟的瞬态分析[J]. 中国铁道科学, 2005, 26(6):89-92.

(XIE Ning, FENG Lian, WANG Wandi, et al. Transient Analyses of 3D Numerical Simulation in Tunnel Fire[J]. China Railway Science, 2005, 26(6):89-92. in Chinese)

[8]卢平, 廖光煊, 厉培德, 等. 地铁网络风流不稳定性分析及其控制研究[J]. 中国铁道科学, 2004, 25(2):134-138.

(LU Ping, LIAO Guangxuan, LI Peide, et al. Instability Analysis and Control Research on Airflow in Subway Ventilation Network[J]. China Railway Science, 2004, 25(2):134-138. in Chinese)

[9]HERWIG H, GLOSS D, WENTERODT T. A New Approach to Understand and Model the Influence of Wall Roughness on Friction Factors for Pipe and Channel Flows[J]. Journal of Fluid Mechanics, 2008, 613(6): 35-53.in Chinese)

[10]邹江, 彭晓峰, 颜维谋. 壁面粗糙度对通道流动特性的影响[J]. 化工学报, 2008, 59(1):25-31.

(ZOU Jiang, PENG Xiaofeng, YAN Weimou. Effects of Roughness on Fluid Flow Behavior in Ducts[J]. Journal of Chemical Industry and Engineering(China), 2008, 59(1):25-31. in Chinese)

[11]冯炼, 刘应清. 地铁通风网络的数值分析[J]. 中国铁道科学, 2002, 23(1):131-135.

(FENG Lian, LIU Yingqing. Numerical Simulation Analysis of Ventilation Network in Subway[J]. China Railway Science, 2002,23(1):131-135. in Chinese)

[12]冯炼, 刘应清. 地铁阻塞通风的数值模拟[J]. 中国铁道科学, 2002, 23(3):120-123.

(FENG Lian, LIU Yingqing. Study on Ventilation Blocking Computation in Subway[J]. China Railway Science, 2002, 23(3):120-123. in Chinese)

[13]KANDLIKAR S G. Roughness Effects at Microscale Reassessing Nikukadse’s Experiments on Liquid Flow in Rough Tubes[J]. Bulletin of the Polish Academy of Sciences Technical Sciences, 2005, 53 (4):343-348.

[14]HU Y, WERNER C, LI D. Influence of the Three Dimensional Heterogeneous Roughness on Electrokinetic Transport in Microchannels[J]. Journal of Colloid and Interface Science, 2005, 280(2): 527-536.