基于无刷直流电机的伺服系统低速性能仿真研究

王 括，田胜利，李 清，王 鑫

（北京精密机电控制设备研究所，北京，100076）

基于无刷直流电机的伺服系统低速性能仿真研究

王 括，田胜利，李 清，王 鑫

（北京精密机电控制设备研究所，北京，100076）

伺服系统低速运动时，无刷直流电机转速低，运动平稳性差，容易产生力矩波动，引起低速爬行现象。为解决这一问题，在伺服系统位置环的基础上引入电流环，其中电流环采用分时反馈策略，根据霍尔信号逻辑对三相电流进行选择；位置环采用神经网络比例、微分、积分控制，并仿真验证伺服系统性能。仿真表明通过双闭环及神经网络PID控制能较好改善系统性能。

低速；双闭环；分时反馈；神经网络PID

0 引 言

机电伺服系统是以电动机为动力驱动元件的伺服系统，目前广泛应用于火箭、导弹、机器人等领域[1]。与有刷电机相比，无刷直流电机采用电子换相，消除了机械电刷带来的摩擦影响；与永磁同步电机相比，无刷直流电机控制不必进行复杂空间矢量变换，控制方法简单，且其永磁体为均匀的瓦片形结构，较易制造，因此无刷直流电机在机电伺服系统中的应用越来越广泛[2～7]。

由于电机力矩存在波动，受摩擦、电机换相、驱动电路等限制，伺服系统低速运行过程中经常出现爬行现象，因此引入电流闭环限制力矩波动[8]。

对于大部分机电伺服系统，应用传统比例、微分、积分（Proportion Integral Derivative，PID）控制通常可以满足其要求，PID控制结构简单，对误差控制有鲁棒性，通过调整比例、积分、微分系数可以改变系统的响应特性。然而实际伺服系统中通常存在非线性、参数的时变及不确定性，因此传统PID可能无法适应高性能指标的要求。

近年来，神经网络发展迅速，在医学、图像处理、人工智能等领域已有广泛应用。人工神经网络可以逼近任意复杂的非线性关系，然而单纯的神经网络控制存在对初值选择敏感、不易收敛等弊端，因此将神经网络与PID控制结合运用。通过反向传播（Back Propagation，BP）神经网络在线调整比例、积分、微分系数，选择合适的初值使其达到收敛效果。

本文通过采集相电流并通过霍尔信号得到电流分时反馈，位置环采用神经网络PID控制，通过仿真与普通PID控制进行对比，达到优化效果。

1 无刷直流电机伺服系统

机电伺服系统通常由电机、控制器、驱动器、传感器、传动装置等组成，位置-电流双闭环系统结构如图1所示。

图1 伺服系统结构

根据无刷直流电机原理建立电压、电流与转矩方程：

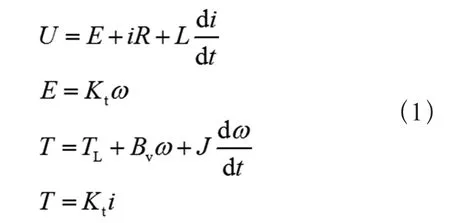
式中 U为母线电压；ω为电机转速；i为相电流；E为感应电动势；T为电磁转矩；L为电枢电感；R为电枢电阻；Kt为转矩系数；J为转动惯量；TL为负载转矩；Bv为阻力系数。

忽略负载力矩，并经过拉普拉斯变换及简化得到电机转速与电压关系的数学模型：

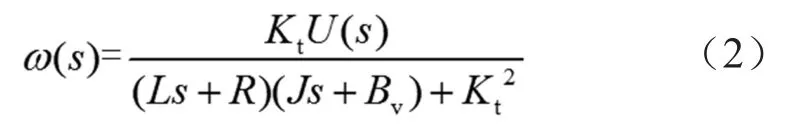
2 分时电流获取方法

由于伺服系统母线电流中含有控制驱动器消耗的电流，因此需要通过电流采集芯片采集相电流，根据霍尔传感器信号逻辑可以得到当前时刻导通相，通过模拟通道的数据选择器可以选出当前正向相电流。

根据霍尔信号逻辑图得到数据选择器选通端输入信号与三相霍尔信号关系式：

式中 B，A为数据选择器选通端输入信号；HA， HB，HC为三相霍尔信号逻辑；分别为HA， HC取反。

图2为电流选择电路。

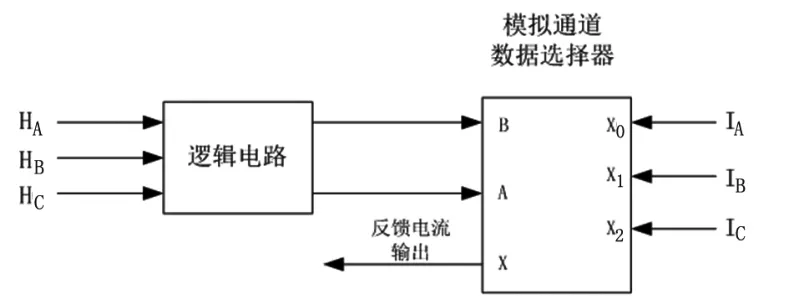
图2 电流选择电路

3 基于神经网络的PID算法

神经网络PID算法从结构上可以分为输入层、隐含层、输出层3层，通过调节神经元网络权值改变神经网络输出即PID参数。图3为神经网络PID系统原理。

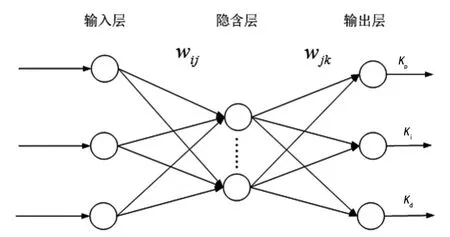
图3 神经网络PID原理

隐含层及输出层的活化函数分别用正负对称的sigmoid函数和非负的sigmoid函数表示，活化函数能够增强网络的映射功能，同时提高收敛速度。取性能指标函数其中，r(k)为位置指令输入；y(k)为位置反馈；e(k)为误差。根据最速下降法修正网络权值系数，沿负梯度方向搜索，控制策略采用加入惯量项的方法，使BP网络训练时振荡较小。权值修正公式为

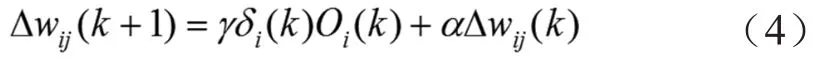
式中 Δwij为网络间权值的变化量；Oi为第i个神经元的实际输出；δi为第i个神经元的权值修正的局部梯度；γ为学习速率；α为惯量因子。

采用直接PID控制，根据梯度运算方法可得输出层局部梯度：

式中 INi(k)为输出层神经元的输入；u(k)为PID控制输出；y(k)为位置反馈；epidi(k)(i=1,2,3)分别为位置误差、位置误差变化率、位置误差积分。

隐含层局部梯度：

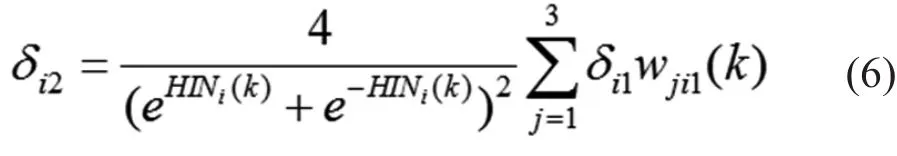
式中 HINi(k)为隐含层神经元输入；wji1(k)为输出层权值。

根据以上分析，在本文中BP神经网络PID控制算法在Simulink中可以通过下述步骤进行：

a）步骤1：选定BP网络结构为3-5-3，即3个输入层神经元，5个隐含层神经元，3个输出层神经元。给出各神经元权值的初值，均选取为0.5，同时选定学习速率η=0.99，惯性系数α=0.000 1；

b）步骤2：采样得到位置指令r(k)，位置反馈y(k)，计算e(k)=r(k)-y(k)。

c）步骤3：计算BP神经网络各层神经元输入、输出值，其中输出层的输出为控制参数Kp，Ki，Kd。

d）步骤4：采用直接式PID控制，根据误差e(k)计算出控制量输出u(k)，u(k)=Kp.e(k)+Ki.Σe(k)+Kd. (e(k)-e(k-1))。

e）步骤5：进行神经网络在线学习，根据权值修正公式得到修正后的权值。

f）步骤6：令k=k+1，返回步骤2。

系统采用电流环与位置环双闭环控制，由于位置环对系统产生决定性影响，因此位置环应用神经网络PID控制与普通PID进行比较，电流环控制采用比例、积分（Proportion Integral，PI）控制。

4 仿真结果

根据机电伺服系统原理建立主要包括控制器模块、脉冲宽度调制（Pulse Width Modulation，PWM）产生模块、功率管逻辑开关模块、三相驱动模块、电机本体模块、机械传动模块的整体伺服系统，其Simulink模型如图4所示。

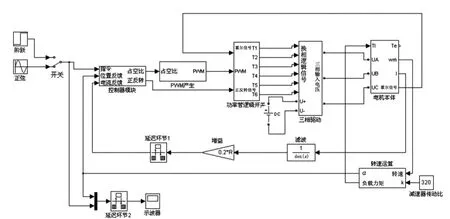
图4 双闭环系统Simulink模型

选用maxon某型号电机，电机及传动机构折算至电机轴上的转动惯量为2.7×10-7kg·m2，其中，相间电阻ra=2.71 Ω，相间电感La=2.31×10-4H，反电动势系数ke=0.013 3 (V·s)/rad，转矩系数KT=0.013 3 (N·m)/A，阻力系数Bv=5×10-9N·m·s。为与实际系统对应，选择位置反馈信号采样时间为1 ms，分辨率为0.01°，摩擦采用Stribeck模型作为负载力矩叠加至系统中。电流采集部分通过前文所述方式，采集三相电流并进行选择，得到电流反馈。

位置控制器分别应用普通PID和神经网络PID，在参数初值相同情况下进行小角度位置信号仿真。初值选取Kp=10，Ki=0.05，Kd=0.024神经网络PID参数浮动范围为Kp=5～15，Ki=0.025～0.075，Kd=0.012～0.036。

输入0.1°，4 Hz正弦信号，图5、6分别为神经网络PID及普通PID仿真结果。由于位置指令角度较小且频率不高，因此可以认为伺服系统处于低速运行状态，可以明显看到普通PID平顶宽度较大，同时相角滞后较小。图7为神经网络PID参数变化。

图5 0.1°，4Hz神经网络PID控制

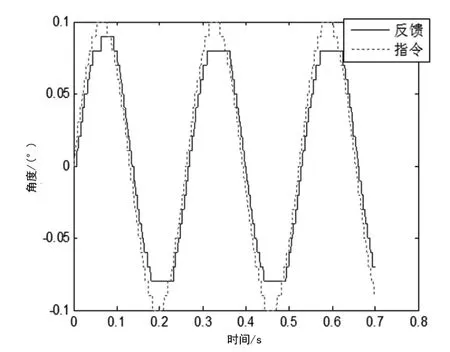
图6 0.1°，4Hz普通PID控制

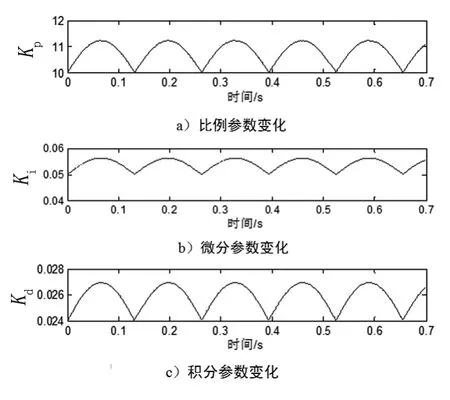
图7 神经网络PID参数变化

5 结束语

根据仿真结果可以看出，位置输入为小幅值正弦信号时，神经网络PID能实时改变PID参数，更好地跟踪给定信号，改进系统的低速性能。同时可以看出PID参数随时间变化曲线，其趋势为指令速度低时增大控制参数，使得系统对小误差信号响应效果更好。

[1] 黄玉平, 李建明, 朱成林. 航天机电伺服系统[M]. 北京: 中国电力出版社, 2013.

[2] 夏长亮. 无刷直流电机控制系统[M]. 北京: 科学出版社, 2009.

[3] 深秀风. 永磁无刷直流电机电磁转矩脉动抑制技术的研究[D]. 哈尔滨:哈尔滨理工大学, 2009.

[4] 王亮, 宗元. 电机低速运行“爬行”现象的研究[J]. 仪器仪表与分析监测, 2011(3): 18-21.

[5] 陶桂林. 无刷直流电机及其系统研究[D]. 武汉: 华中科技大学, 2004.

[6] 周小庆. 高速无人机电动舵机控制器的设计与实现[D]. 杭州: 浙江大学, 2010.

[7] 吴森堂. 飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2005.

[8] Wang S, Li T C, Wang Z G. Commutation torque ripple reduction in brushless DC motor drives using a single current sensor[J]. Electric Machines & Control, 2008, 37(6): 16-17.

Research on the Performance at Low Speed of the Servo System Based on the Brushless Direct Current Motor

Wang Kuo, Tian Sheng-li, Li Qing, Wang Xin
(Beijing Research Institute of Precise Mechatronics and Controls, Beijing, 100076)

When the servo system moves in low speed, there will be low speed of BLDCM, bad motion stability, torque ripple and phenomenon of slow moving. To solve the problem, current loop based on the servo position loop is used. Current feedback in turn can be used in the current loop and the three-phase current can be chose based on Hall signal. Using Neural Network PID controller in the position loop and the system performance will be proved by simulation. The simulation shows that system performance can be improved by double closed-loop and neural network PID.

Low speed; Double closed-loop; Current feedback in turn; Neural network proportion integral derivative

V448.22

A

1004-7182(2016)05-0092-04

10.7654/j.issn.1004-7182.20160519

2016-05-15；

2016-06-08

王 括（1991-），男，助理工程师，主要研究方向为机电伺服机构