基于瑞利准则的火箭发动机稳定性缩比方法研究

安红辉，聂万胜

（1.中国人民解放军装备学院研究生院，北京，101416；2.中国人民解放军装备学院航天装备系，北京，101416）

基于瑞利准则的火箭发动机稳定性缩比方法研究

安红辉1，聂万胜2

（1.中国人民解放军装备学院研究生院，北京，101416；2.中国人民解放军装备学院航天装备系，北京，101416）

针对高压补燃循环火箭发动机燃烧稳定性试验提出一种基于瑞利准则的稳定性缩比方法，通过量纲分析得到决定稳定性相似的关键参数，给出缩比尺度的确定方法。通过缩比准则，可使推进剂种类和喷前温度不变、喷注速度不变、混合比不变，喷注器和燃烧室同全尺寸发动机分别几何相似，缩比发动机燃烧室压力大于推进剂超临界值。算例分析结果表明，该方法得到的缩比发动机燃烧室的压力和流量等大幅降低。

瑞利准则；缩比尺度；几何相似；喷注速度；稳定性

0 引 言

高频不稳定燃烧是火箭发动机研制过程中的一项重要课题，会引起燃烧室爆炸等严重后果，其产生机理复杂，主要通过试验验证[1]。缩比发动机技术始于20世纪五六十年代，是按照某种缩比方法将全尺寸发动机设计成小尺寸试验发动机，由于其流量小、室压低，从而降低了试验难度，具有较大的应用价值[2,3]。根据研究目的的不同，缩比的方法很多，本文主要研究稳定性缩比方法。稳定性缩比方法分为2种：a）开口式燃烧室[4～8]，采用声学相似方法确定不同类型喷嘴稳定性边界；b）针对全尺寸发动机某一特定声学特性进行缩比的燃烧室，包括单喷嘴轴向燃烧室、脉冲燃烧室、二维片状燃烧室和楔形燃烧室等[9～11]。文献[12]运用轴向燃烧室研究了液-液双旋喷嘴结构对稳定性的影响。由于缩比燃烧室其结构的局限性，因此难以做到燃烧流场完全相似。

瑞利准则认为，对封闭气体进行周期性加热和放热，则封闭气体压力也会产生周期性振荡，振荡程度取决于压力振荡和热传递之间的相位关系。如果二者同相位，即压力最大时吸热或者压力最小时放热，压力振荡将会加剧；反之，如果二者反相位，即压力最大时放热或者压力最小时吸热，压力振荡将会减小[13]。火箭发动机燃烧过程在封闭燃烧室内进行，当燃烧室释放和燃烧室声学压力周期振荡耦合同相时，燃烧室压力急剧振荡且局部温度急剧升高，即产生高频不稳定燃烧。因此认为瑞利准则是诱发火箭发动机燃烧不稳定的主要原因。本文基于瑞利准则，通过量纲分析得出1种火箭发动机稳定性缩比方法，并进行了算例分析。

1 缩比方法

缩比发动机能够全部或部分再现全尺寸发动机燃烧稳定性试验过程中遇到的稳定性问题，而且缩比试验结果能够逆推到全尺寸发动机，以指导其设计。缩比发动机必须按照一定相似性原则进行缩小，才能保证缩比试验的意义。

1.1 缩比原理

火箭发动机高频不稳定燃烧是燃烧室内推进剂雾化蒸发混合燃烧过程和燃烧室声学模态之间相互作用的结果，瑞利准则认为高频燃烧稳定性取决于燃烧室内燃烧热释放同燃烧室内高频声学振荡间的相位差，当相位差为零时，造成燃烧室压力高频振荡和局部温度急剧升高，即发生高频不稳定燃烧，目前这一准则得到普遍认可。本文以瑞利准则作为高频不稳定燃烧的唯一判定准则，提出一种高压补燃循环液体火箭发动机稳定性缩比方法，认为在2种相似的燃烧流场，只要满足瑞利准则就稳定性相似。

1.2 基本假设

本文基于瑞利准则，提出1种火箭发动机稳定性缩比方法，该方法的基本假设如下：

a）对于气液同轴离心式喷嘴，喷嘴间的相互影响可以忽略；

b）忽略燃烧室平均压力对声场的影响，将燃烧室内压力振荡作为声场主要参数；

c）喷嘴内气体通道纵向声学模态同燃烧室切向声学模态相位一致；

d）推进剂混合比不变时，发动机燃烧室内温度保持不变；

e）燃烧室壁面无加质或加质条件相似，出口无回流发生；

f）喷管喉部面积变化较小时，对燃烧流场的影响可以忽略；

g）对于火箭发动机燃烧室内部高温高压环境，液体推进剂喷前已经接近或处于超临界状态，以稠密气体状态进入燃烧室，可看作是气-气混合，雾化蒸发过程快，化学动力学过程也很快，以至于雾化蒸发时间可以忽略不计，混合时间是燃烧延迟的主要控制因素；

h）高压补燃液体火箭发动机预燃室燃烧后，一方面形成高温混合气体（简称为“气氧”）轴向喷入主燃室喷嘴（见图1）；另一方面液体燃料经过冷却通道温度升高，在喷嘴末端沿周向布置的切向孔进入喷嘴同轴向运动的高温气氧混合温度继续升高，达到超临界状态，此时混合物处于稠密气体状态，整个喷嘴通道内部充满气体，喷嘴内通道截面直径形状变化和末端缩进尺寸相对喷嘴特征尺寸较小，可忽略喷嘴内通道的截面变化和末端缩进，喷嘴内气道为等直径声谐振管。

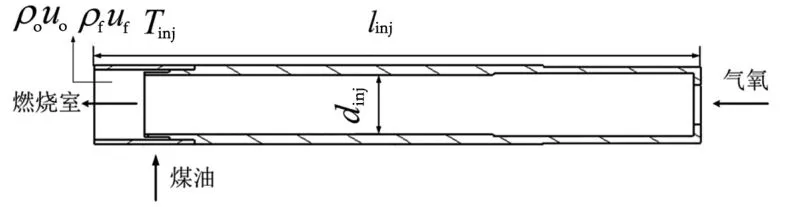
图1 同轴式喷嘴

1.3 量纲分析

火箭发动机燃烧室内燃烧是不稳定燃烧产生之源，由瑞利准则，高频不稳定燃烧产生的必要条件是燃烧室内的热释放和燃烧室内声学振荡同相，即二者相位差决定着不稳定燃烧的产生，相位差越小压力振荡越剧烈。这种相位关系可以表述为热释放周期和压力振荡周期的关系，同时认为燃烧开始即意味着热释放的开始，将推进剂进入燃烧室经过雾化蒸发混合等过程到燃烧开始的时间差定义为燃烧延迟时间，这样相位差可转化为燃烧延迟时间和燃烧室声学振荡周期之间的关系。令燃烧延迟特征时间为τ，燃烧室声学振荡周期为t，频率为fch，则热释放和压力振荡之间的相位关系为θ=2πτ/t，这就是稳定相似性的相位关系。

如前所述，燃烧延迟时间主要受混合时间影响，令燃烧室射流混合区沿燃烧室轴向特征长度为le，射流特征速度为u，则有：

其中，le同射流初始当量直径de成正比例关系，则有：

当射流1喷入射流2时，有：

式中 ρ1和ρ2分别为2种混合射流密度。

设u为表征组分射流混合的有效速度或射流混合区波动的传播速度，u的大小和两种射流的密度之比ρ2/ρ1和各自的射流速度u2/u1有关[4]。

在声学谐振管原理中，其结构会对燃烧室声学模态产生声学影响，从而可得如下计算公式：

a）燃烧室切向声学频率计算公式：

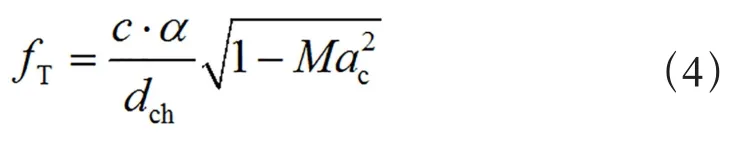
b）喷嘴纵向声学频率计算公式：

c）声速计算公式：

式中 α为贝赛尔函数根值;Mac为喷嘴气道内马赫数；dch为燃烧室直径；Δl为同气道直径有关的修正值；γ为比热比；R为气体常数。

由于燃烧室和喷嘴气道内马赫数Mac很小，可忽略不计，在气体不变时，声速和温度有关。因此影响喷嘴气道和燃烧室切向声学相位关系的因素主要有燃烧室直径dch、燃烧室完全燃烧长度Lw、全尺寸发动机喷管收敛段长度Lc、全尺寸发动机燃烧室圆筒段长度Lch、燃烧室内燃气温度Tch和喷嘴气道长度linj等，如图2所示。

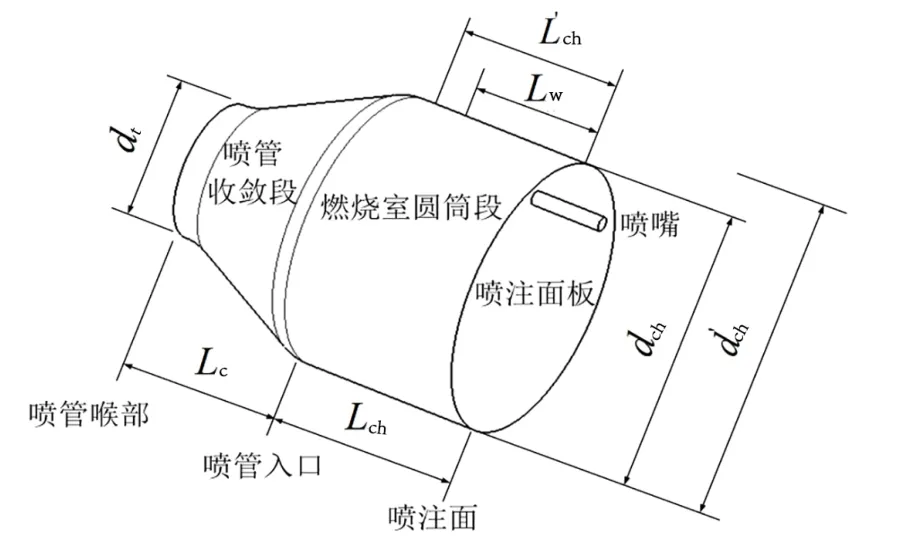
图2 全尺寸燃烧室示意

燃烧室内热释放和高频声学振荡之间的相位关系是稳定性的唯一控制因素，影响相位关系的物理量有ρo，ρf，uo，uf，dinj，dch，linj，Tinj和Tch，即相位差和这些物理量的函数关系式为：θ=f (ρo，ρf，uo，uf， dinj，dch，linj,Tinj，Tch)，所有物理量中包含质量M、长度L、时间T和温度Θ 4个基本单位。选取ρf，uf，dinj和Tinj为基本物理量进行量纲分析，应用π值定理得到以下5个无量纲量：

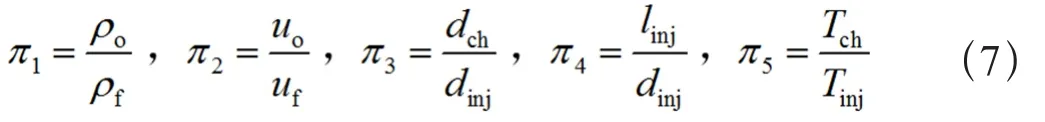
由上述分析可知，只要保证π1，π2，π4和π5相同就能保证θ值不变。所以只要氧化剂和燃料密度比、射流速度比、燃烧室和喷嘴直径之比、喷嘴长径比、喷嘴和燃烧室内温度之均保持不变，以及前文提到的混合比不变，就能保证稳定性相似。而2个气-气燃烧流场相似的必要条件是推进剂种类和温度不变，推进剂喷注速度不变，喷注器和燃烧室分别几何相似[13]。注意到推进剂种类、喷前温度和混合比不变能够保证π1和π5不变，推进剂喷注速度不变能够保证π2不变，喷注器和燃烧室分别几何相似能够保证π3和π4不变。由此可知如下流速公式：

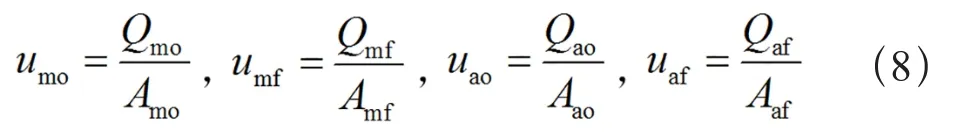
式中 umo，umf，uao和uaf分别为缩比发动机和全尺寸发动机氧/燃料的射流速度；和分别为缩比发动机和全尺寸发动机氧/燃料的体积流量；Amo，Amf，Aao和Aaf分别为缩比发动机和全尺寸发动机喷注器氧/燃料的出口面积。

在推进剂射流速度不变时，喷嘴喷注面积为原缩比尺度r2倍时，则体积流量为全尺寸发动机的r2倍。

综上所述，本文基于瑞利准则缩比方法原则为：推进剂种类相同、推进剂喷前温度不变，喷注器和燃烧室分别几何相似，推进剂喷注速度不变，混合比不变，缩比燃烧室压力超过喷入燃烧室液体燃料的临界压力值。

1.4 缩比尺度确定

缩比尺度定义为缩比发动机和全尺寸发动机对应特征长度之比。由前文相似性分析可知，只要保证几何相似，缩比尺度可以无限小，但是实际中火箭发动机内燃气达到完全燃烧需要一定长度，所以在确定缩比尺度之前首先要确定完全燃烧长度Lw，缩比发动机燃烧室长度Lm应满足Lm≥Lw，才能保证流场相似。通常一阶切向不稳定燃烧对火箭发动机最具破坏力，是主要研究对象，所以在缩比试验中还要保证一阶切向不稳定模态首先激发。缩比尺度确定方法主要有相似法和模态法2种，无论哪种方法都要保证燃料完全燃烧和一阶切向不稳定燃烧室的首先激发。相似法是根据燃烧室几何相似准则，由完全燃烧长度确定缩比尺度r；模态法是通过适当选取燃烧室直径和长度来保证缩比发动机首先激发一阶切向振荡的设计方法，即保证缩比燃烧室一阶切向振荡频率f1T小于其一阶纵向振荡频率f1L，即fT＜fL。

根据发动机声学模态计算公式，则有：

可以得到在dch＞1.17Le时fT＜fL。当fT＜fL时采用相似法进行缩比尺度r计算，反之采用模态法进行缩比尺度r计算，其中，Le为全尺寸发动机燃烧室当量长度。

采用相似法计算缩比尺度r时，r=L＇ch/Lch；其中，L＇

ch为缩比发动机燃烧室圆筒段长度，L＇ch取燃气完全燃烧长度至全尺寸发动机燃烧室圆筒段长度之间的任意值，如图2所示。

采用模态法计算缩比尺度r时，按照dch＞1.17Le原则，由Lch确定d＇ch值，保证d＇ch＞1.17Lch，缩比尺度r=d＂ch/dch（其中，d＂ch为缩比发动机燃烧室直径，d＂ch取小于值d＇ch），如图2所示。

1.5 缩比参数推算到全尺寸发动机

运用缩比发动机进行稳定性评定试验，将试验得到的稳定性区域对应的缩比发动机参数逆推到全尺寸发动机，得到全尺寸发动机的稳定性区域参数。发动机结构尺寸推算按照几何相似原则进行计算，对应全尺寸推进剂流量参数推算如下（式中N为喷嘴个数）：

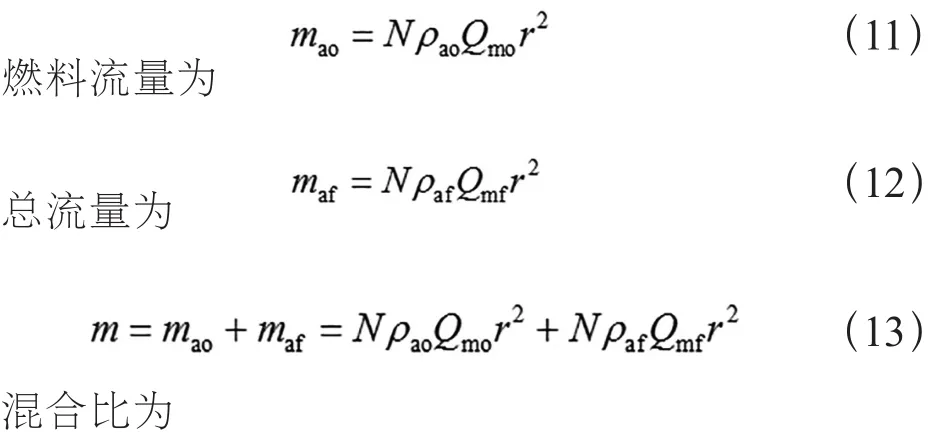
氧流量为

2 算例分析

某型号高压补燃循环火箭发动机，推进剂为液氧/煤油，单喷嘴氧流量为891.6 g/s，煤油流量为891.6 g/s，混合比2.6，室压17.72 MPa，其他参数详见文献[9]，由于气液同轴离心式喷嘴的相互独立性，确定单个喷嘴的基准参数，其他喷嘴计算相同。

根据本文缩比方法，缩比发动机推进剂选择氧气/煤油，喷前温度均为657.3 K，混合比为2.6，缩比燃烧室压力取略高于煤油临界压力2.5 MPa，缩比燃烧室燃气完全燃烧长度为100 mm。由式（10）得，dch＞1.17Le，缩比尺度r=0.5。2种发动机的主要参数对比如表1所示。

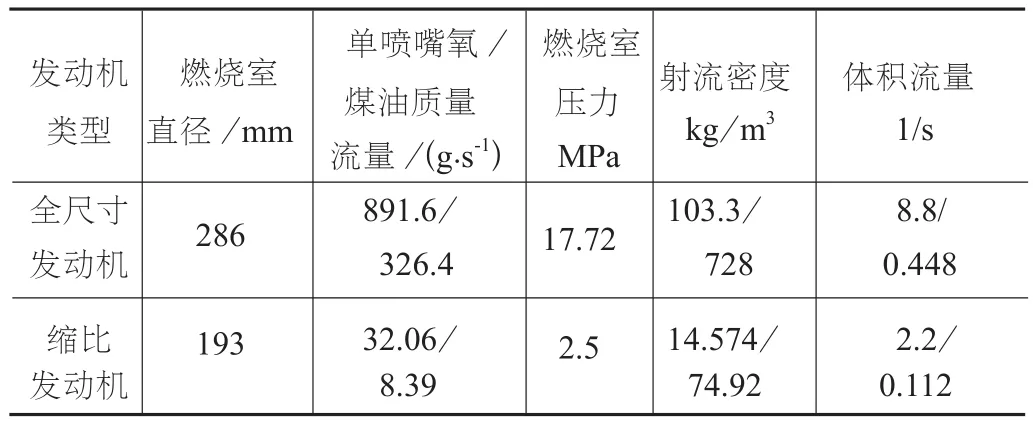
表1 2种发动机主要参数对比

由表1可知，运用本文得到的缩比发动机燃烧室尺寸、压力、推进剂质量流量等大为降低。

3 结 论

本文基于瑞利准则，通过量纲分析得出其中一种发动机稳定性缩比设计方法：a）确定缩比尺度；b）推进剂种类、喷前温度、喷注速度和混合比均不变。喷注器和燃烧室同全尺寸发动机几何结构相似，缩比发动机燃烧室压力大于推进剂超临界值；c）将缩比发动机参数推算到全尺寸发动机。算例分析表明，缩比发动机燃烧室压力、流量等大为降低，但是本文缩比方法适用于气-气推进剂和高压补燃循环液体火箭发动机。试验时根据研究需要，可以选择不同的喷嘴类型和喷嘴布局形式。

[1] Culick F E C, Yang V. Overview of combustion instabilities in liquidpropellant rocket engines[C]. Washington: Progress in Aeronautics and Astronautics, 1995.

[2] Penner S S. Similarity analysis for chemical reactors and the scaling of scaling of liquidliquid fuel rocket engines, combustion research and reviews[M].Butterworths: AGARD Combuston Colloquium, 1995.

[3] Penner S S. Chemical problems in jet propulsion[M]. London: Pergamon Press, 1957.

[4] Dravnovsky M L. Combustion instabilities in liquid rocket engines: testing and development practices in russia[M]. Washington: Progress in Aeronautics and Astronautics, 2007.

[5] 王枫, 李龙飞, 张贵田. 液氧煤油补燃发动机喷注器高频燃烧不稳定性的试验研究[J]. 宇航学报, 2012.

[6] Robert E, Jr B. Laboratory scale injector instability mode assessment[D]. Huntsville: The University of Alabama, 2008.

[7] Sohn C H, Young J K. A scaling method for combustion stability rating of coaxial gas-liquid injectors in a subscale chamber[J]. Journal of Mechanical Science and Technology, 2012,26(11): 3691-3699.

[8] Chul J K, Chae H S. Combustion-stability rating of impinging-jet injectors using scaling techniques in a subscale chamber[R]. AIAA 2011-5550, 2011.

[9] Dexter C E, Fisher M F, Hulka J R, Denisov K P, Shibanov A A, Agarkov A F. Thrust chambers: aspects of modeling, analysis, and design[M]. Washington: Progress in Astronautics and Aeronautics, 2004.

[10] 哈杰D T, 里尔登 F H. 液体推进剂火箭发动机不稳定燃烧[M]. 朱宁昌, 张宝炯, 译, 北京: 国防工业出版社, 1981.

[11] Wierman M, Feldman T, Anderson W. Development of combustion response functions in a subscale high pressure longitudinal combustor[R]. AIAA 2013-3778, 2013.

[12] Ahna K. Hana Y M. Effects of injector recess and chamber pressure on combustion characteristics of liquid-liquid swirl coaxial injectors[J]. Combustion Science and Technology, 2010.

[13] 蔡国飙, 汪小卫, 李茂, 等. 液体火箭发动机气气燃烧及气气喷注器技术[M]. 北京: 国防工业出版社, 2012.

Study on the Stability-scaling Method of Rocket Engine Based on Rayleigh Criterion

An Hong-hui1, Nie Wan-sheng2
(1. Equipment Academy of PLA, Department of Postgraduate, Beijing, 101416; 2. Equipment Academy of PLA, Department of Space Equipment, Beijing, 101416)

The stability-scaling test method based on Rayleigh criterion is presented for the test on combustion stability of high-pressure staged combustion rocket engine. The key parameters that determine the stability are obtained by dimensional analysis and the method determining the scale ratio is given. By criterion， the type of propellant, injection temperature, speed, mixing ratio are the same as full-size combustors; the injector and combustors are geometrically similar to the full size engine. The pressure of the scaled device is higher than the critical one of the propellant. The results indicate that the pressure and the flow rate of the scaled combustor are reduced greatly.

Rayleigh criterion; Scale ratio; Geometric similarity; Injection speed; Stability

V43

A

1004-7182(2016)05-0023-05

10.7654/j.issn.1004-7182.20160505

2015-12-02；

2016-08-14

国家自然科学基金项目（91441123）

安红辉（1981-），男，博士，主要研究方向为液体火箭发动机燃烧稳定性