基于EEMD和Husrt指数的GNSS基准站的垂向速率估计

彭　葳，戴吾蛟

(中南大学 地球科学与信息物理学院,湖南 长沙 410083)



基于EEMD和Husrt指数的GNSS基准站的垂向速率估计

彭葳，戴吾蛟

(中南大学 地球科学与信息物理学院,湖南 长沙 410083)

摘要：连续的全球卫星导航系统(GNSS)基准站的坐标时间序列中包含了复杂的噪声信号、非构造形变及其它因素的影响，尤其在垂直方向，对GNSS基准站在国际地球参考框架(ITRF)下的运动速率估计产生了较大的干扰。为进一步提高速率精度，文中采用整体模态分解(EEMD)方法对GNSS基准站的垂向观测时间序列进行分解，并根据各种信号的Hurst值进行分类及重构为噪声信号、季节性信号和长期趋势信号，采用最小二乘方法拟合长期趋势信号得到垂向速率。通过对中国大陆构造环境监测网络(CMONOC)的GNSS台站从2001—2013年近13 a的垂向坐标时间序列的实例分析，采用基于EEMD和Husrt指数的最小二乘法能够准确地估计GNSS基准站的垂向速率。

关键词：整体经验模态分解；Hurst指数；负荷改正；速率估计；最小二乘法

GNSS台站的坐标和运动速率的准确估计可以用于参考框架的维持及地壳板块运动的研究等方面。在国际参考框架(ITRF)下，GNSS时间序列在东方向(E)和北方向(N)的年变化量为厘米级，而噪声和季节性变化为毫米级，故在N、E方向的速率估计较为准确；但垂向的形变较小(毫米级)，而噪声和季节性变化影响却达到厘米级。Nikolaidis根据GNSS时间序列中的噪声、周期变化、趋势变化的特性，建立了GNSS坐标时间序列的几何模型，并采用加权最小二乘法求解，可以估计出站点运动速率[1]。但是GNSS观测序列中的噪声和周期变化会影响速率的估计，为了提高估计几何模型中速率的估计精度，需要准确地分析观测时间序列的噪声和周期形变。GNSS坐标序列中的噪声的估计方法有很多种，包括功率谱、极大似然估计、最小二乘方差分量估计等方法[2-3]。而GNSS坐标时间序列中的季节性变化主要由大气负荷、土壤水负荷、非潮汐海洋负荷、积雪负荷等因素的影响[4]，许多研究者将季节性变化归结于GNSS台站之间的共模误差，并采用主成分分析等方法将共模误差削弱[5]。在削弱共模误差之后，顾及有色噪声拟合GNSS台站的几何模型，可以估计出GNSS站的速率[6]。但这些方法估计GNSS站的垂向速率仍需要顾及较多的多余参数，影响速率的估计。

GNSS时间序列中的隐含信号包含着特有的物理特征，采用时间序列分析方法可以分析GNSS时间序列中的隐含信息[7]。本文根据GNSS时间序列中包含的隐含信号(白噪声、有色噪声、周期形变和长期趋势形变等)存在着不同的时频特征，采用整体经验模态分解(EEMD)根据信号的时频特征进行分解[8]；同时，GNSS时间序列中包含的隐含信号又存在着不同的分形特征，采用Hurst指数可以对EEMD方法分解的子信号进行归类。本文从单站的单维GNSS时间序列分析的角度出发，采用EEMD方法分解单维的GNSS垂向的观测时间序列，得到一组固有模态分量(IMF)，然后通过估计EEMD分解的IMF分量的Hurst指数，可以较为准确地提取噪声序列[9]。而参考去噪后的负荷改正模型的Hurst指数，能够准确提取GNSS的坐标时间序列中的非构造形变。而准确地分析噪声和非构造形变能够减少GNSS几何模型中的参数，从而提高模型的精度，对于形变较小的GNSS垂向时间序列的速率项的估计有着重要的作用。

1GNSS垂向时序速率估计模型

根据GNSS垂向时间序列的特征，本文建立的GNSS垂向时间序列的速率估计流程如图1所示。

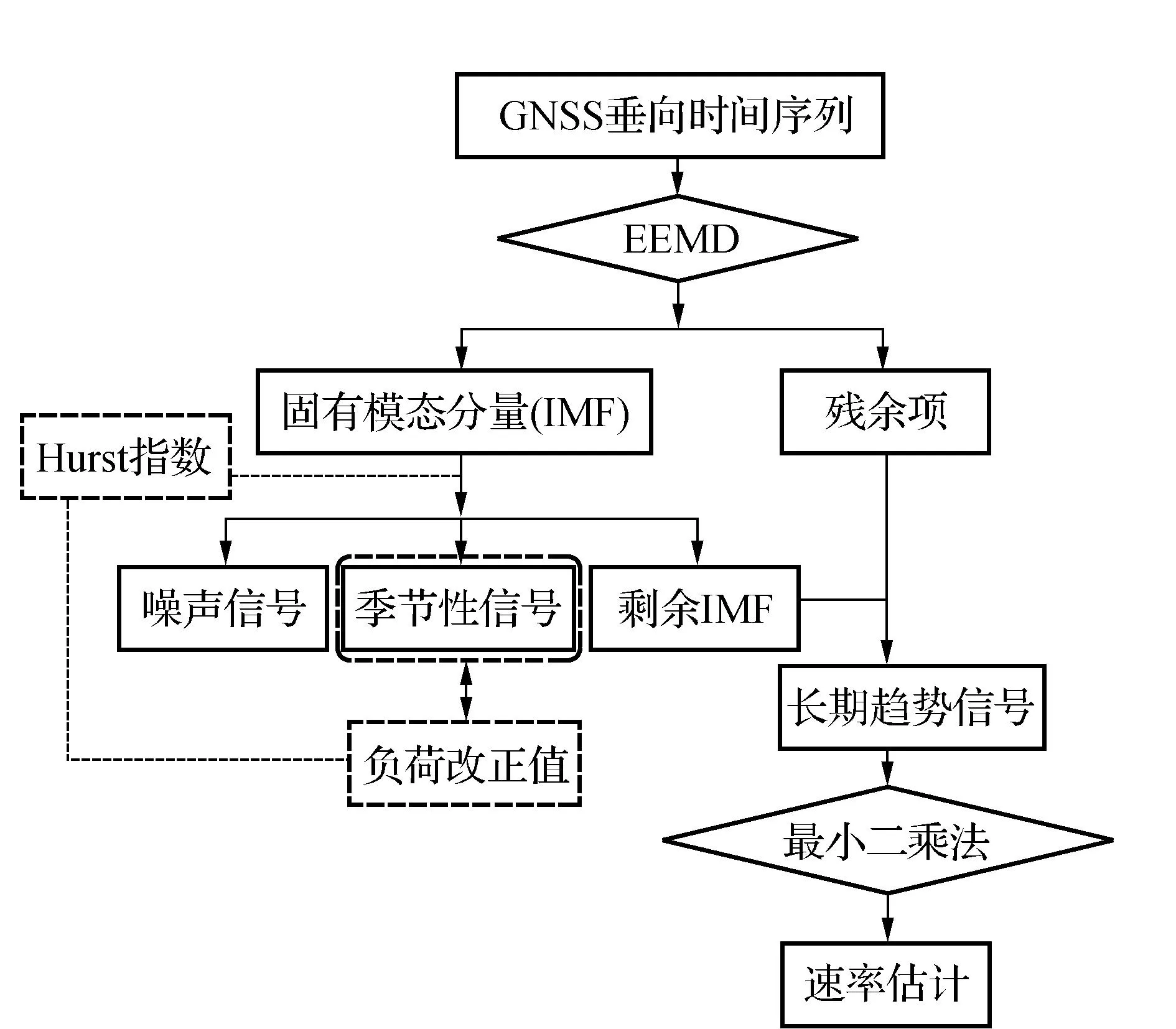
图1　GNSS垂向时间序列的速率估计流程

1.1经验模态分解

经验模态分解(EMD)是一种广泛用于从含有噪声的非线性、非平稳的数据中提取信号的自适应的时频分析方法[10]。假设一组时间序列x(t)，EMD方法它是根据信号的时频特征将时间序列x(t)分解成若干个子序列和残差序列，而这些不同频率的子序列也被称为固有模态函数(IMF)。

EMD的一般公式为

(1)

其中:di(t)为第i个IMF分量，rn(t)为残差序列。

EMD分解的主要步骤如下：

1)寻找信号中的所有极大值和极小值，拟合成上包络线emax(t)和下包络线emin(t)。

3)计算时间序列与上下包络线均值的差值d(t)=x(t)-m(t)。

4)重复1)～3)，迭代残余值m(t)。

EMD可以从信号中分解频率从高到低的IMF分量，高频的IMF分量一般认为是噪声信号，中低频的IMF分量需要物理因素来进行分析解释，但是EMD方法存在着模态混叠的问题，这会使得IMF分量的物理意义不明确。为了解决EMD方法的不足，Wu等提出了整体经验模态分解(EEMD)方法[8]。

首先，在时间序列x(t)加入不同的白噪声序列。

(2)

其中，wi(t)为第i次加入的白噪声，且每次随机加入的白噪声的方差相同。

然后，将得到的xi(t)进行EMD分解，得到N组IMF分量，取N组中对应尺度的IMF分量的均值，得到EEMD分解的最终IMF分量。EEMD分解的信号可以表示为

(3)

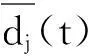
1.2噪声和非构造形变的Hurst指数分析

Hurst指数会发生在许多应用数学的领域，包括分形和混沌理论、长记忆过程和谱分析。随机过程也可以产生自相似分形，其中一个重要的例子是布朗运动(Brown motion)。分数布朗运动(fractional Brown motion,fBm) 是非平稳的随机过程，而分数高斯噪声(fractional Gaussian noise,fGn) 是一个零均值平稳过程，可看作为分数布朗运动的增量。

GNSS时间序列的分数高斯噪声序列的频率和功率谱密度的关系可以描述为[11]

(4)

其中，α为谱指数。

消除趋势波动分析(DFA)方法是一种分形标度指数计算方法，通常用于检测非平稳时间序列的自相似性，可用于时间序列的物理特征的分析。DFA方法计算的Hurst指数(H)可以描述噪声序列的分形特征，也作为噪声分类及提取的依据。Hurst指数与噪声的关系可以描述为

(5)

在上式的定义下，H=0.5为白噪声，H=1为闪烁噪声，H=1.5为随机游走信号[9]。白噪声和闪烁噪声与环境负荷效应的影响相关性不强，且白噪声加闪烁噪声模型(WN+FN)符合大多数GNSS基准站数据中的噪声特征[12]，故将H≤1的IMF分量作为噪声信号提取[13]；此公式定义下的随机游走信号可能与负荷效应有关，需要进一步分析[14]。

在中国大陆地区，环境负荷(大气负荷、土壤水负荷、积雪负荷等)对地壳的影响在几年至十几年的时间范围内是较为平稳的，负荷影响的地壳季节性变化也具有特有的物理特征(频率和功率谱密度之间的关系)。通过Hurst指数进行信号特征分析，重新组合EEMD分解的IMF分量，可以快速提取GNSS时间序列中的非构造形变。

1.3最小二乘速率估计

GNSS单测站的任一分量的几何模型可以表示为[1]

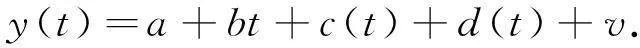
其中：a为初始偏差；b为速率；c(t)为年周期和半年周期项；d(t)为其他项，包括偏移项、震后速率变化等等；v为残差项，且在残差项中还包含有白噪声和有色噪声[15]。

在准确估计出噪声序列和非构造形变序列之后，GNSS单测站的某一分量的坐标时间序列y′(t)可以表示为

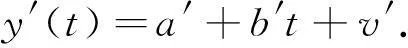
其中：a′为初始偏差；b′为速率；v′为残差，且v′中不包含噪声信号。采用最小二乘方法对上式求解，求出速率项系数b′。

2非构造形变分析

本文选取了中国大陆构造环境监测网络的17个站的垂向时间序列，从2001年至2013年的垂向时间序列作为实例分析。GNSS垂向时间序列的变化都表现为含有白噪声、有色噪声、周期波动和长期趋势运动[16]。采用EEMD方法对GNSS垂向时间序列进行分解，加入的白噪声与信号的标准差的比例为0.2，平均次数为200次。图2为作为示例的EEMD方法分解的BJFS、JIXN、KMIN 3个站的垂向时间序列的IMF和残差项，其余14个站的EEMD分解的情况与之相似。

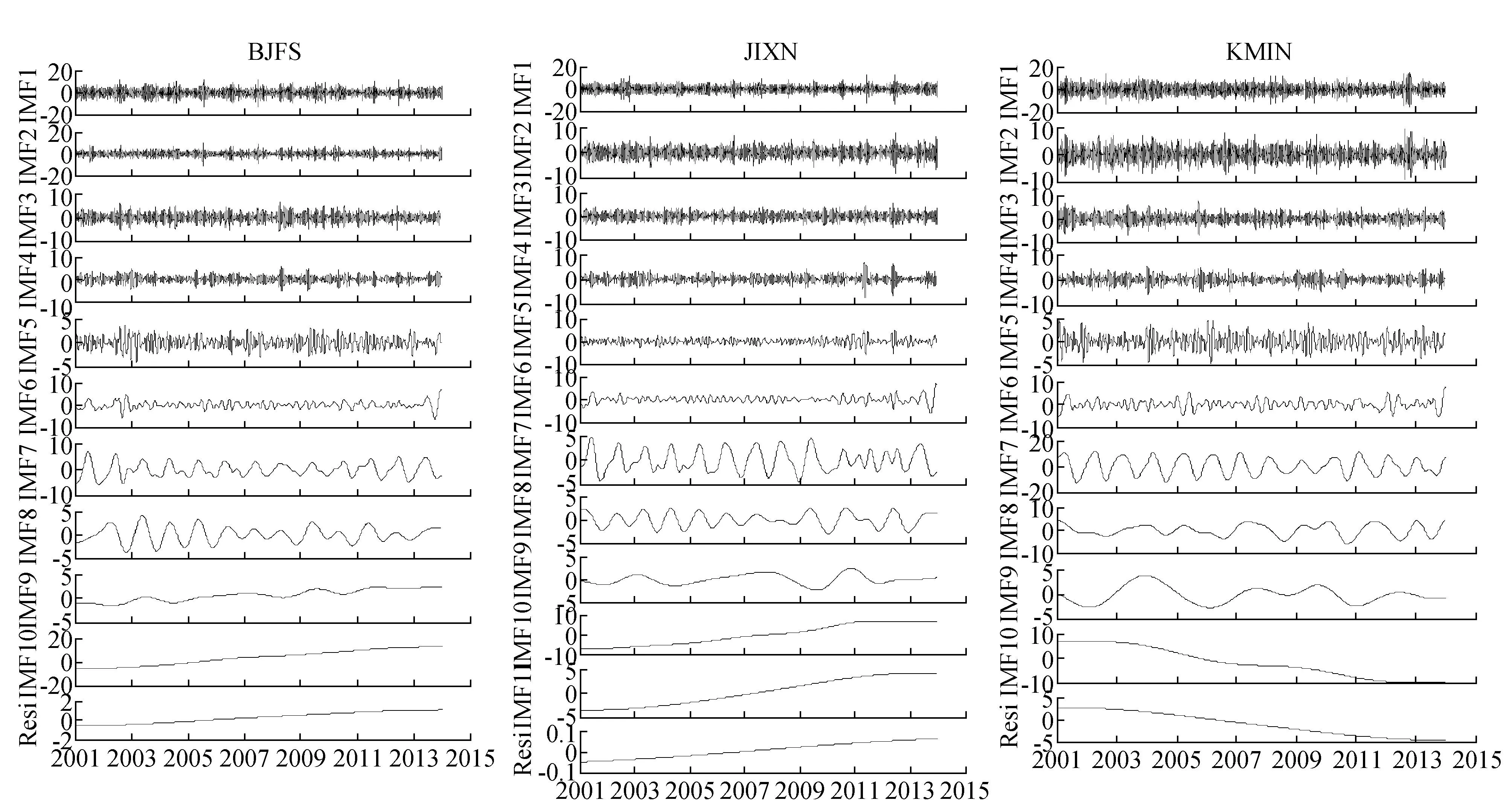
图2　EEMD方法分解的GNSS站(BJFS、JIXN、KMIN)的垂向时间序列的IMF分量及残差项(Resi)

计算EEMD分解的IMF分量的Hurst值，将H≤1的IMF分量重构为噪声信号，然后将剩余IMF重新编号(1,2,3,…)，如图3所示。

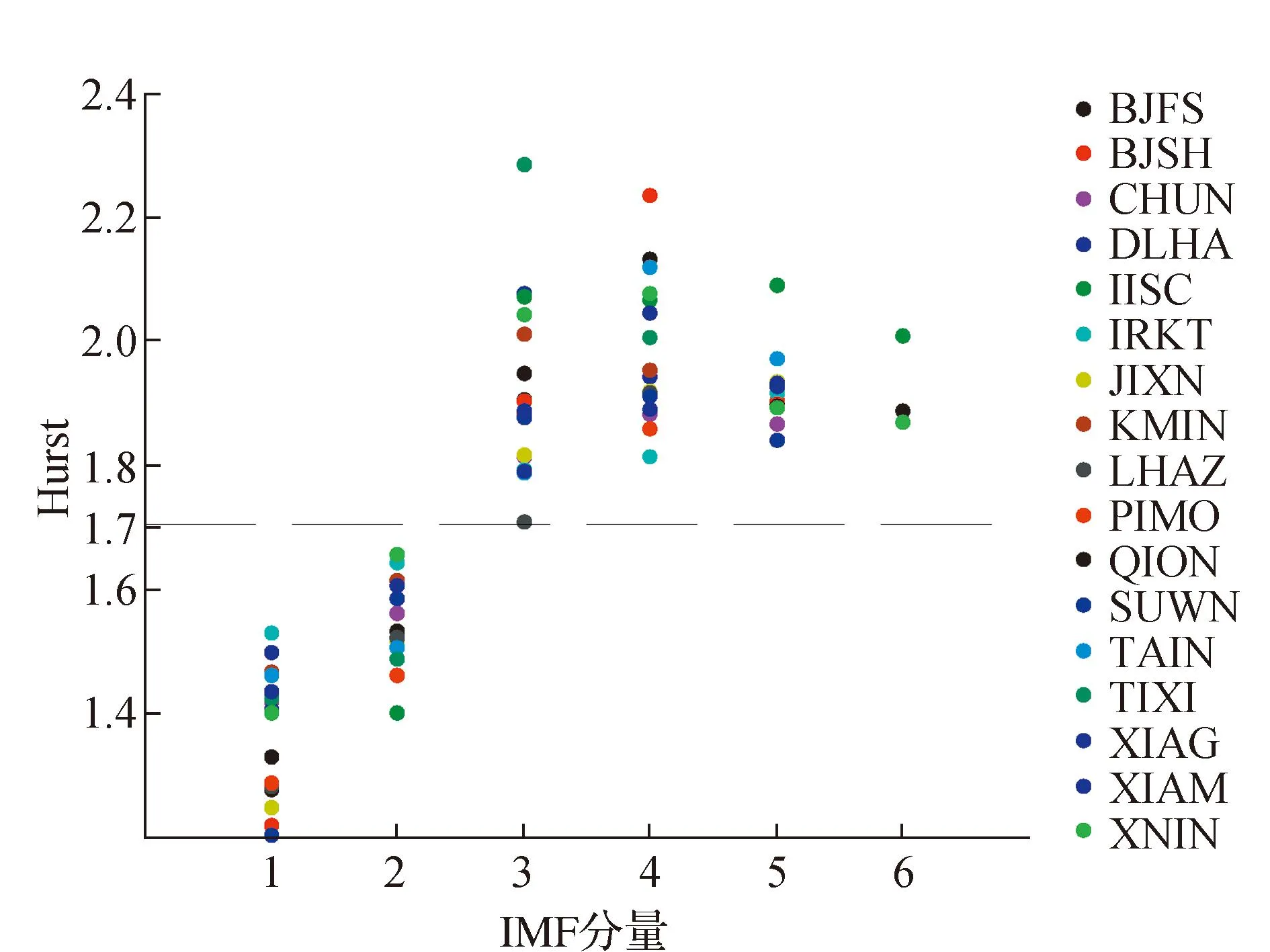
图3　去噪后的剩余IMF分量的Hurst值

从图3中可以发现各个站的剩余的IMF分量中，第2个IMF分量和第3个IMF分量会产生明显的分离，而这个分离的界限的Hurst值约为1.7，故可以选取H≤1.7作为区分非构造形变和趋势形变的界限值。

为了验证信号区分的准确性，本文引入环境负荷的改正模型，用于对比分析EEMD方法和Hurst指数提取的GNSS垂向时间序列中的非构造形变信号。QOCA软件是一款GPS数据的后处理软件，它能够较为准确地计算各种负荷效应的改正值。大气负荷、土壤水负荷、积雪负荷的数据从NCEP(National Center for Environmental Prediction) 获得。

1) 大气地表压力数据的采样时间间隔为6 h，空间的分辨率为2.5°×2.5°；

2) 土壤水数据的采样间隔为1 d，空间的分辨率为1.875°×1.875°；

3) 积雪数据的采样间隔为1 d，空间的分辨率为1.875°×1.875°。

通过QOCA求出各种负荷每天的均值，得到时间分辨率为1 d的负荷改正值的时间序列。同样采用EEMD方法和Hurst指数滤除信号中的噪声，计算17个GNSS监测站的剩余分量之和的Hurst值，其均值约为1.4，与H=1.7界限存在着差异的可能原因如下：

1) EEMD将非构造形变分解成多个IMF分量；

2) DFA方法计算Hurst指数存在计算误差(δH≤0.1)[17]。

通过对比图4中环境负荷改正值总和与使用本文方法提取的非构造形变信号，可以看出通过EEMD和Hurst指数的方法提取的非构造形变信号与环境负荷的改正值信号在波形上高度相似，说明该方法能有效地提取非构造形变。

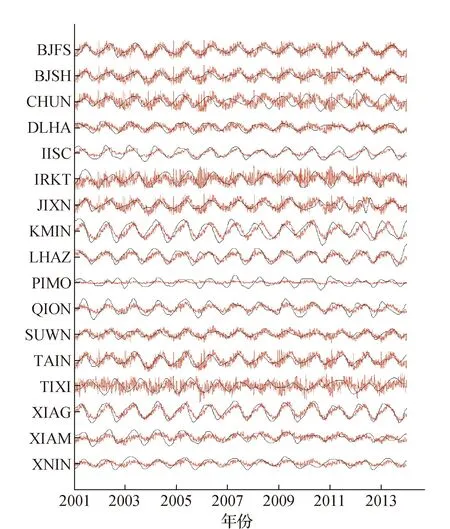
图4　环境负荷改正值总和(红色线)与EEMD+Hurst方法提取的季节性信号(黑色线)的对比图

3GNSS时间序列分析及速率估计

3.1模拟实验

根据GNSS基准站的垂向时间序列的信号特征[16]，本文模拟了白噪声、闪烁噪声、季节性形变和趋势信号。其中白噪声由MATLAB产生，闪烁噪声由文献[13]中的递归方法产生，季节性信号是由QOCA软件(http://gipsy.jpl.nasa.gov/qoca/)解算的长春站(CHUN)的去噪后的负荷改正值，趋势信号由直线模拟。模拟的两个信号中，一个加入的是较小的趋势信号，另一个加入较大的趋势信号，模拟的时间长为4 747 d，模拟的两个不同速率的信号如图5所示。

EEMD方法对两个模拟信号进行分解，加入的白噪声与信号的标准差的比例为0.2，平均次数为100次。模拟信号1被分解成11个IMF分量和1个残余项，模拟信号2被分解成9个IMF分量和1个残余项。计算得到的IMF分量的Hurst值，提取H≤1的噪声信号，因为是模拟数据是模拟中国地区的GNSS监测站,故直接提取H≤1.7的IMF分量为非构造形变信号；剩余的IMF分量重构为趋势信号，并采用最小二乘法进行拟合。将本文方法计算结果与CATS软件计算结果进行对比，CATS (The Create and Analyze Time Series) 是一款采用最小二乘拟合时间序列的多参数模型，同时顾及了残差时间序列的噪声序列[18]，图6给出了对比的结果。

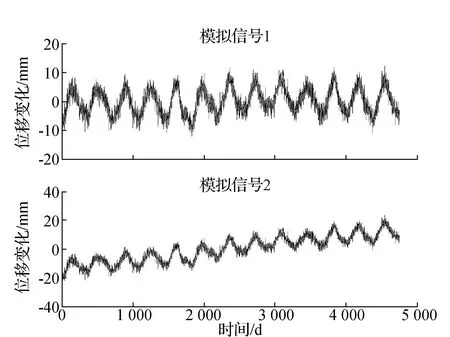
图5　模拟的两个不同速率的模拟信号

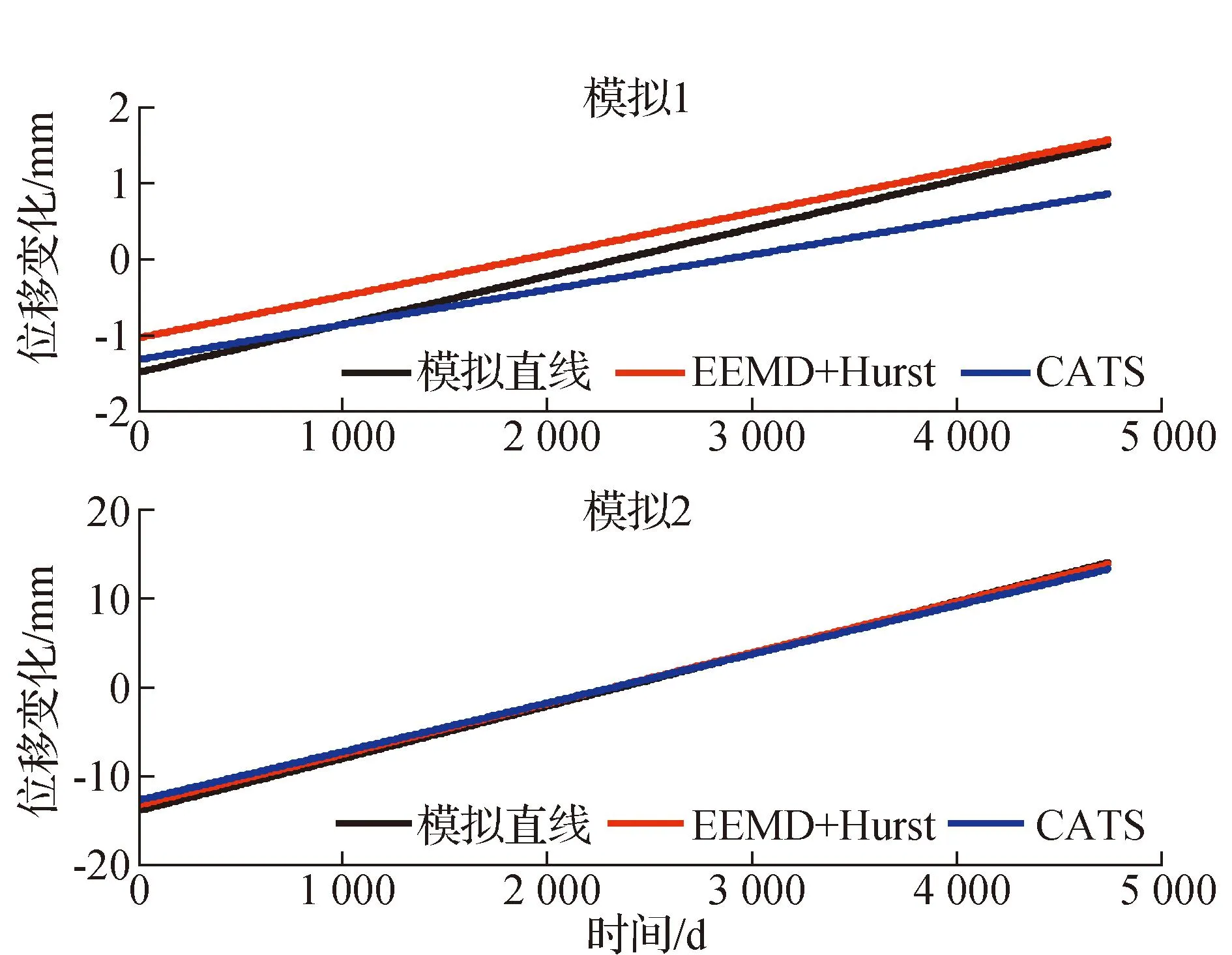
图6　基于EEMD和Hurst指数的最小二乘拟合的直线(红线)、CATS拟合的直线(蓝线)与模拟直线(黑线)的对比

图6显示的是基于EEMD和Hurst指数的最小二乘拟合的直线(红线)、CATS拟合的直线(蓝线)与模拟直线(黑线)的对比，可以发现红线和黑线的斜率(速率)更为接近，它们的值如表1所示。

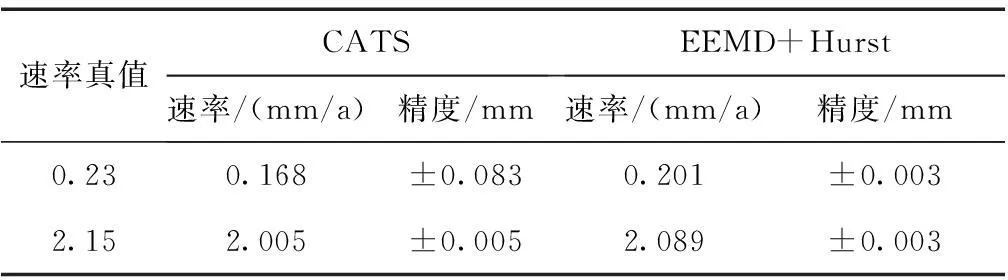
表1　基于EEMD和Hurst指数最小二乘拟合方法与CATS得到的垂向速率及拟合精度的对比

通过模拟实验可以说明EEMD+Hurst方法估计得到的速率更趋近于真值，且该方法的拟合精度要高于CATS的精度。

3.2GNSS垂向时间序列的速率估计

在准确地估计了GNSS垂向时间序列中的噪声信号和非构造形变信号后，采用最小二乘估计速率。图7为作为示例的BJFS、JIXN、KMIN原始坐标序列、长期趋势信号和拟合直线的对比。

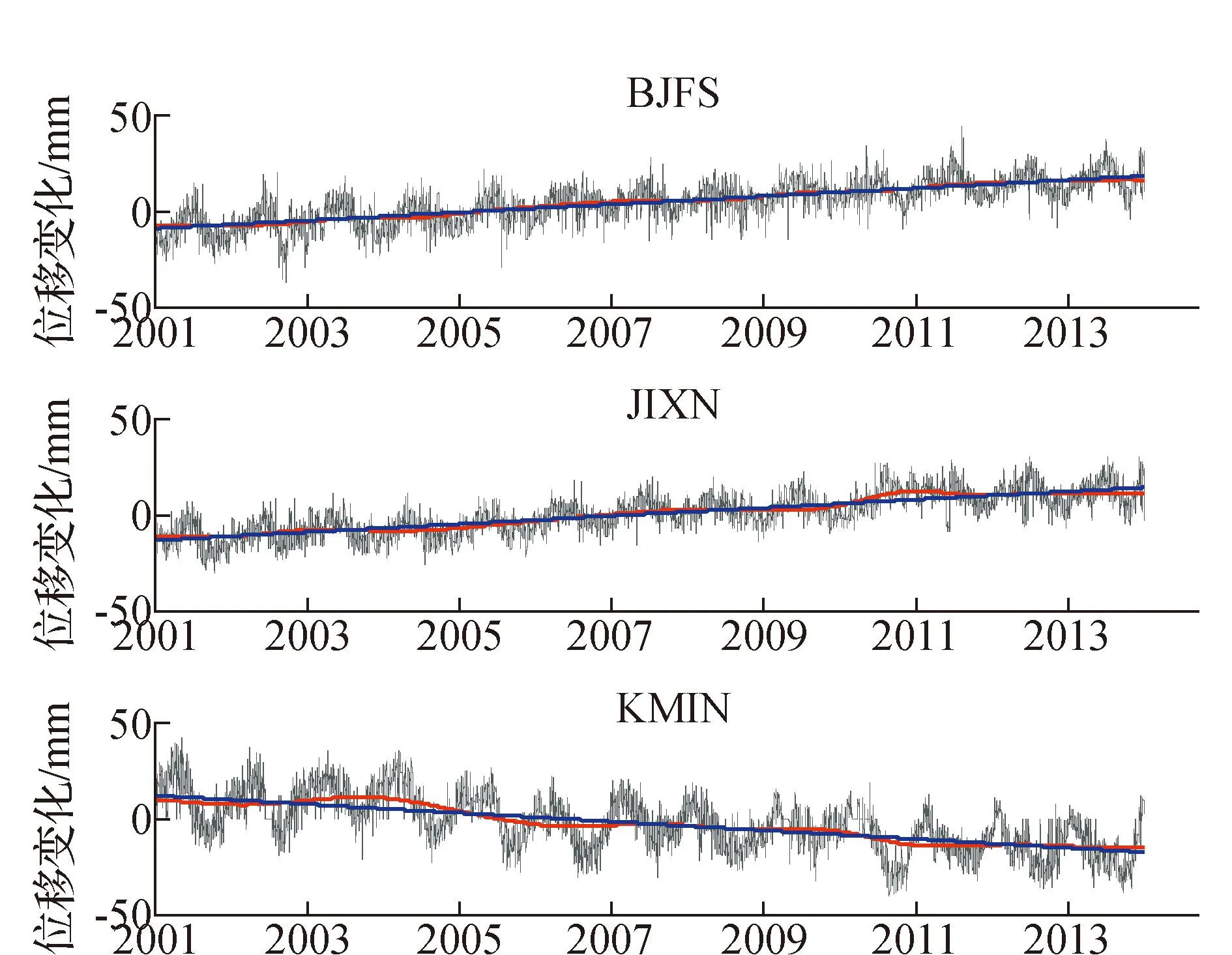
图7　原始时间序列(灰线)、长期趋势信号(红线)和拟合直线(蓝线)的对比

从图7中可以看出，提取的长期趋势信号能较好地反映原始时间序列的趋势变化的特征，且拟合的直线与长期趋势信号的相似度也很高，说明使用基于EEMD和Hurst指数的垂向速率估计是较为准确的。

为了验证EEMD和Hurst指数的垂向速率估计方法得到的GNSS时间序列的垂向速率的有效性和准确性，将本文方法计算结果与CATS软件计算结果进行对比，对比结果如表2所示。

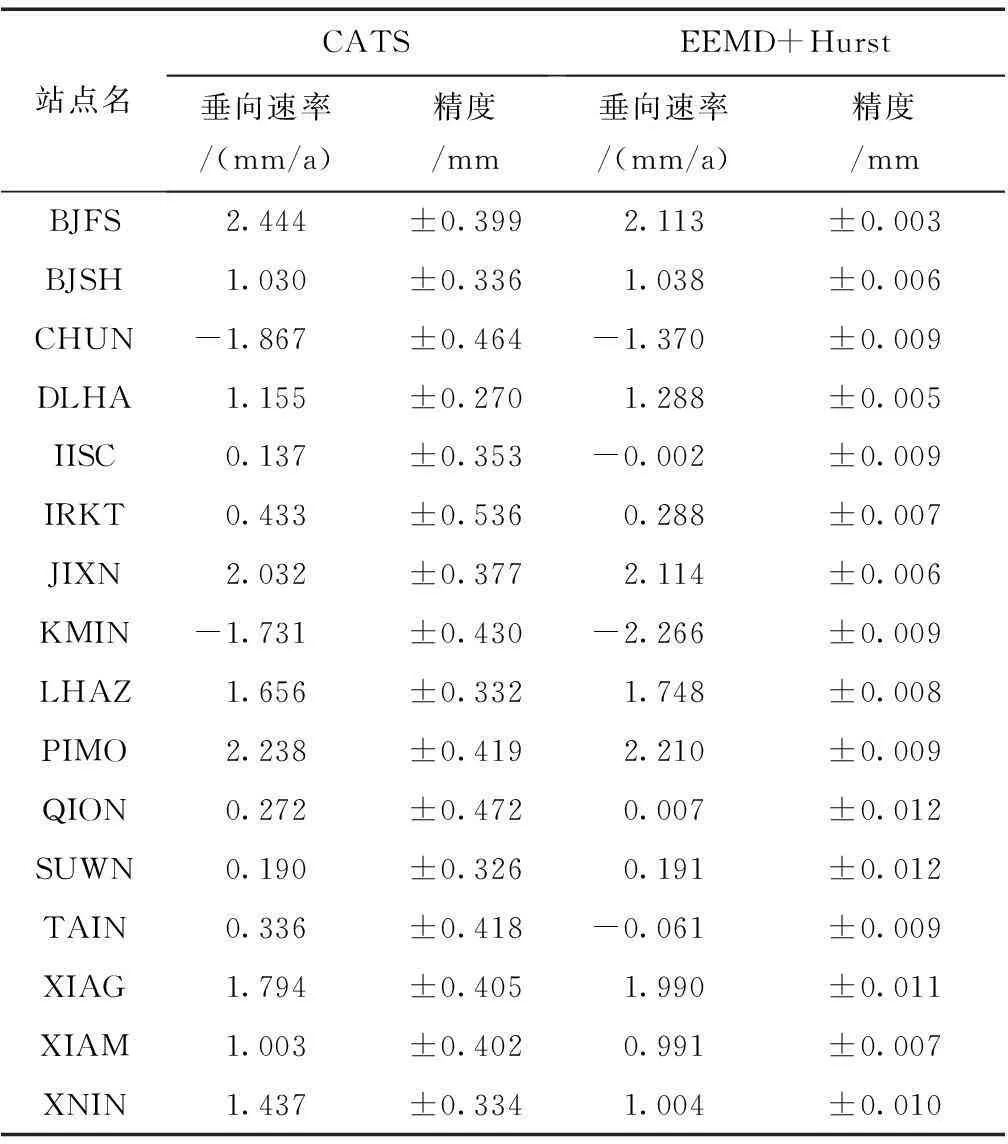
表2　基于EEMD和Hurst指数最小二乘拟合方法与CATS得到的垂向速率及拟合精度的对比

从表2中可以看出，采用基于EEMD和Hurst指数的最小二乘法估计的垂向速率和CATS软件估计的垂向速率很接近。但是，当站台的运动速率变化较小时，CATS软件的拟合精度相对垂向速率较大，影响了垂向速率分析的准确性；而本文算法由于准确提取了趋势信号，拟合精度较高，能较为准确地估计趋势变化垂向速率。

4结论

通过基于EEMD和最小二乘方法模型可以准确地分析GNSS垂向时间序列及估计速率项。通过对中国大陆构造环境监测网络(CMONOC)的17个站的垂向时间序列的分析及模拟试验，可以得到以下两个结论：①Hurst指数及环境负荷可以有效地对EEMD分解的IMF分量中的噪声和非构造形变信号进行识别和提取；②基于EEMD+Hurst的最小二乘法得到的垂向能够较好地反映地壳趋势运动变化，得到的垂向速率的拟合精度较高，这对于有些垂向形变较小的GNSS参考站的速率估计有非常大的意义。

参考文献：

[1]NIKOLAIDIS R.Observation of geodetic and seismic deformation with the Global Positioning System[D].San Diego：University of California,2002.

[2]ZHANG J,BOCK Y,JOHNSON H,et al.Southern California Permanent GPS Geodetic Array：Error analysis of daily position estimates and site velocities[J].Journal of Geophysical Research：Solid Earth (1978～2012),1997,102(B8)：18035-18055.

[3]TEUNISSEN P J G,AMIRI-SIMKOOEI A R.Least-squares variance component estimation[J].Journal of Geodesy,2008,82(2)：65-82.

[4]DONG D,FANG P,BOCK Y,et al.Anatomy of apparent seasonal variations from GPS‐derived site position time series[J].Journal of Geophysical Research：Solid Earth (1978-2012),2002,107(B4)：ETG 9-1-ETG 9-16.

[5]袁林果,丁晓利,陈武,等.香港 GPS 基准站坐标序列特征分析[J].地球物理学报,2008,51(5)：1372-1384.

[6]蒋志浩,张鹏,秘金钟,等.顾及有色噪声影响的CGCS2000下我国CORS站速度估计[J].测绘学报,2010,39(4)：355.

[7]章浙涛,朱建军,卢骏,等.小波变换在时间序列特征提取中的应用[J].测绘工程,2014,23(6)：21-26.

[8]WU Z,HUANG N E.Ensemble empirical mode decomposition：a noise-assisted data analysis method[J].Advances in adaptive data analysis,2009,1(1)：1-41.

[9]MONTILLET J P,TREGONING P,MCCLUSKY S,et al.Extracting white noise statistics in GPS coordinate time series[J].Geoscience and Remote Sensing Letters,IEEE,2013,10(3)：563-567.

[10] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London.Series A：Mathematical,Physical and Engineering Sciences,1998,454(1971)：903-995.

[11] AGNEW D C.The time-domain behavior of power‐law noises[J].Geophysical research letters,1992,19(4)：333-336.

[12] 黄立人.GPS 基准站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学,2006,26(2)：31-33.

[13] RODRIGUEZ E,ECHEVERRIA J C,ALVAREZ-RAMIREZ J.1/fαfractal noise generation from Grünwald-Letnikov formula[J].Chaos,Solitons & Fractals,2009,39(2)：882-888.

[14] 田云锋,沈正康.GPS 坐标时间序列中非构造噪声的剔除方法研究进展[J].地震学报,2009,31(1)：68-81.

[15] WILLIAMS S D P.The effect of coloured noise on the uncertainties of rates estimated from geodetic time series[J].Journal of Geodesy,2003,76(9-10)：483-494.

[16] 荣敏,孙付平,贾小林,等.利用GPS基准站数据浅析我国地壳垂直运动[J].测绘工程,2009,18(4)：7-9.

[17] GRECH D,MAZUR Z.On the scaling ranges of detrended fluctuation analysis for long-term memory correlated short series of data[J].Physica A：Statistical Mechanics and its Applications,2013,392(10)：2384-2397

[18] WILLIAMS S D P.CATS：GPS coordinate time series analysis software[J].GPS solutions,2008,12(2)：147-153.

[责任编辑：刘文霞]

Vertical velocity estimation of GNSS reference stationbased on EEMD method and Husrt exponent

PENG Wei,DAI Wujiao

(School of Geosciences and Info-Physics,Central South University,Changsha 410083,China)

Abstract：The daily coordinate time series of Global satellite navigation system (GNSS) reference stations contain the complex effects of noise signals,non-tectonic deformation and other factors,particularly in the vertical direction,of which the factors have a greater impact on the velocity estimation of GNSS reference station on the International Terrestrial Reference Frame (ITRF).In order to improve the accuracy of the velocity estimation,this paper uses the Ensemble Empirical Mode Decomposition (EEMD) method to decompose the vertical time series of GNSS reference station,and the noise signal,seasonal signal and long-term trend signal can be reconstructed respectively based on the Hurst value of signals.Then the vertical velocity can be estimated by using the least square method to fit the long-term trend signals.By analyzing the vertical time series of GNSS stations of Crustal Movement Observation Network of China (CMONOC) from January 2001 to December 2013,the EEMD method and Husrt exponent based on the least square method can accurately estimate the vertical velocity of GNSS reference station.

Key words：EEMD；Hurst exponent；load correction；velocity estimation；least square method

中图分类号：P228

文献标识码：A

文章编号：1006-7949(2016)04-0060-06

作者简介：彭葳(1989-)，男，硕士研究生.

基金项目：国家973计划资助项目(2013CB733303)

收稿日期：2015-02-04；修回日期：2015-03-08