基于RANSAC的残缺平面标靶稳健定位方法

薛晓璐，林　欢

(河海大学 地球科学与工程学院，江苏 南京 210098)



基于RANSAC的残缺平面标靶稳健定位方法

薛晓璐，林欢

(河海大学 地球科学与工程学院，江苏 南京 210098)

摘要：针对圆形有效反射区域的平面标靶拖尾点和因遮挡造成的数据缺失问题，提出一种基于RANSAC的残缺平面标靶稳健定位方法。文中采用RANSAC算法拟合标靶平面，使经过测距误差修正的反射点规整位于标靶平面；利用Givens变换将空间三维圆拟合简化为二维圆RANSAC拟合。采用两个实验分析同一平面标靶因不同遮挡对定位精度的影响。结果表明，该方法能够有效解决拖尾点和数据缺失问题，提高平面标靶定位的鲁棒性。

关键词：平面标靶定位；拖尾点；数据缺失；RANSAC；Givens变换

在高精度扫描的同时会带来边缘拖尾和耗时长的问题，在扫描高速公路隧道、路边建筑等目标时，较长的耗时极易因为车辆行人等障碍物的遮挡造成数据缺失。商用软件在进行平面标靶定位时造成拟合的标靶平面法向偏差，如图1所示。商用软件求取有效反射区域几何中心的方法，对剔除部分拖尾点或数据本身缺失的平面标靶造成中心偏差，如图2所示。

图1　法向偏差

图2　中心偏差

平面标靶定位的研究相对较少。Lichti等利用标准平面标靶的反射特性，提出3种平面标靶定位方法；武汉大学陈西江提出一种分带K—均值聚类的平面标靶定位方法，对噪声点做两次剔除并对经过噪声剔除的点云数据进行分带、聚类处理，通过求取不同分带中心的均值来确定标靶中心；陈俊杰等探讨重心类和几何类方法的平面标靶中心坐标提取方法，认为边缘提取算法不完备，且边缘提取后数据量大量减小会增加结果的不确定性，得出优先使用简单重心法的结论。

平面标靶的定位通过粗差剔除均可在一定程度上提高标靶定位的抗差性。然而在标靶点数据缺失的情况下，则表现出显著的局限性。本文提出一种基于RANSAC的平面标靶定位方法，该方法利用有效反射区域边缘点呈圆形分布的特性，实现数据缺失平面标靶中心的精确稳健定位。

1理论依据

RANSAC算法是一种从包含离群点的数据集中随机选取局内点通过迭代方式估计数学模型的参数。在含有大量粗差的数据集中正确拟合模型参数,RANSAC与最小二乘相比具有显著的优势。传统最小二乘方法将数据集中的所有数据加入到模型参数的计算中，得到最优模型满足所有数据的残差平方和最小。针对最小二乘对粗差的局限性，发展抗差最小二乘理论，增强最小二乘方法对含有粗差数据集的适用性。然而，在本文所要处理的有效数据大量缺失的情况下，以及考虑边缘提取算法的不完备性，提取的边缘点中可能掺进部分非实际边缘点，故采用更为稳健的RANSAC算法进行标靶平面与圆的抗差拟合。

大部分平面标靶都具有中心有效反射区域为圆形的特点，该区域大部分边缘点所在空间圆的圆心即为平面标靶中心。拖尾点由测距误差引起，很大程度上反映平面标靶有效反射区域的边缘特性。RANSAC平面拟合可得到不受拖尾点干扰的绝大部分反射点所在平面。测距误差修正使所有反射点严格落于标靶平面上，可解决拖尾点问题，得到规整的标靶平面。RANSAC圆拟合可克服边缘点提取算法的局限性，拟合得到的圆心坐标即为平面标靶的中心。

2RANSAC标靶平面拟合

2.1平面参数获取

空间平面的表示通常为Hessian形式：

ax+by+cz+d=0.(1)

2.2距离误差修正

拖尾点反映平面标靶有效反射区域的重要几何信息。对每一个反射点Pi(xi,yi,zi)，建立激光束参数方程：

(2)

将式(2)代入式(1)，求得对应于Pi(xi,yi,zi)的修正系数ki值。将ki返回到式(2)即可得到垂足点的坐标。遍历所有反射点，即完成距离误差修正过程。修正后的反射点严格位于RANSAC拟合得到的平面上。

距离修正前后的反射点如图3所示。

图3　距离误差修正

3RANSAC标靶圆拟合与圆心定位

基于空间圆难以直接数学表达的特点以及拟合的复杂性，本文提出一种以Givens变换的方式将空间圆拟合转换为快速稳健的平面圆拟合的方法，拟合方法仍采用具有抗粗差特性的RANSAC。

3.1边缘点提取

本文提出的边缘点提取算法基于极坐标变换，其算法为

1)将距离修正过后的所有点转换为水平角α和垂直角β；

2)按水平角分列，取每一列中所包含点的垂直角极值点作为边缘点，得到点集A；

3)按垂直角分列，取每一列中所包含点的水平角极值点作为边缘点，得到点集B；

4)取边缘点集A∩B。

3.2Givens变换

将标靶平面法向绕x轴和y轴旋转一定的角度α和β，使该法向与z轴平行并与z轴正向同向。矩阵变换：

其中

对每一个边缘点做Givens变换：

其中

3.3RANSAC平面圆拟合

考虑Givens变换后边缘点x坐标和y坐标作平面拟合。与前文所述标靶平面拟合相似，迭代过程亦需设置阈值，此处的阈值为边缘点到拟合圆边界的距离，通过经验可直接设定。

RANSAC平面圆拟合结果为模型的3个参数：圆心坐标(x,y)和半径r。这3个参数可唯一确定该二维平面上的圆。将圆心坐标(x,y)与经过Givens变换得到的z坐标联立，得到三维坐标(x,y,z)。作Givens逆变换，由R1，R2均为正交阵，故

经过上述Givens逆变换，可得平面标靶的实际中心坐标(xc,yc,zc)。

4实验与精度评定

本文实验采用同一完整平面标靶数据，不同程度遮挡造成数据缺失，评价各种情况对精度的影响，

实验过程中RANSAC标靶平面拟合的距离阈值设为0.6，RANSAC圆拟合的距离阈值设为0.8。

4.1实验一

同一完整的平面标靶作不同程度遮挡，利用本文算法求取标靶中心坐标，结果如表1所示。

样本1为完整平面标靶，重心坐标为(-8 179.51,-4 246.48,1 097.49)。对样本1作不同程度的遮挡，如样本2、样本3、样本4及样本5。利用本文提出的算法对5组样本求取标靶中心坐标以及有效反射区域的半径,并计算标靶中心坐标与完整平面标靶中心之间的偏差Δd。

4.2实验二

对样本2、样本3、样本4以及样本5数据缺失类型作缺失率递增，分别计算Δd，变化趋势如图4所示。

由于平面标靶有效反射区域边缘点分布的参差不确定性，在不同遮挡情况下不同边缘点的圆拟合结果也呈现一定的偶然特性。从折线图中可以看出，随着残缺率的递增，Δd呈一定波动性，但定位精度未有明显衰减趋势。当残缺率达到50%时，定位精度仍保持在亚毫米级，表明本文的方法准确有效，具有较强的鲁棒性。

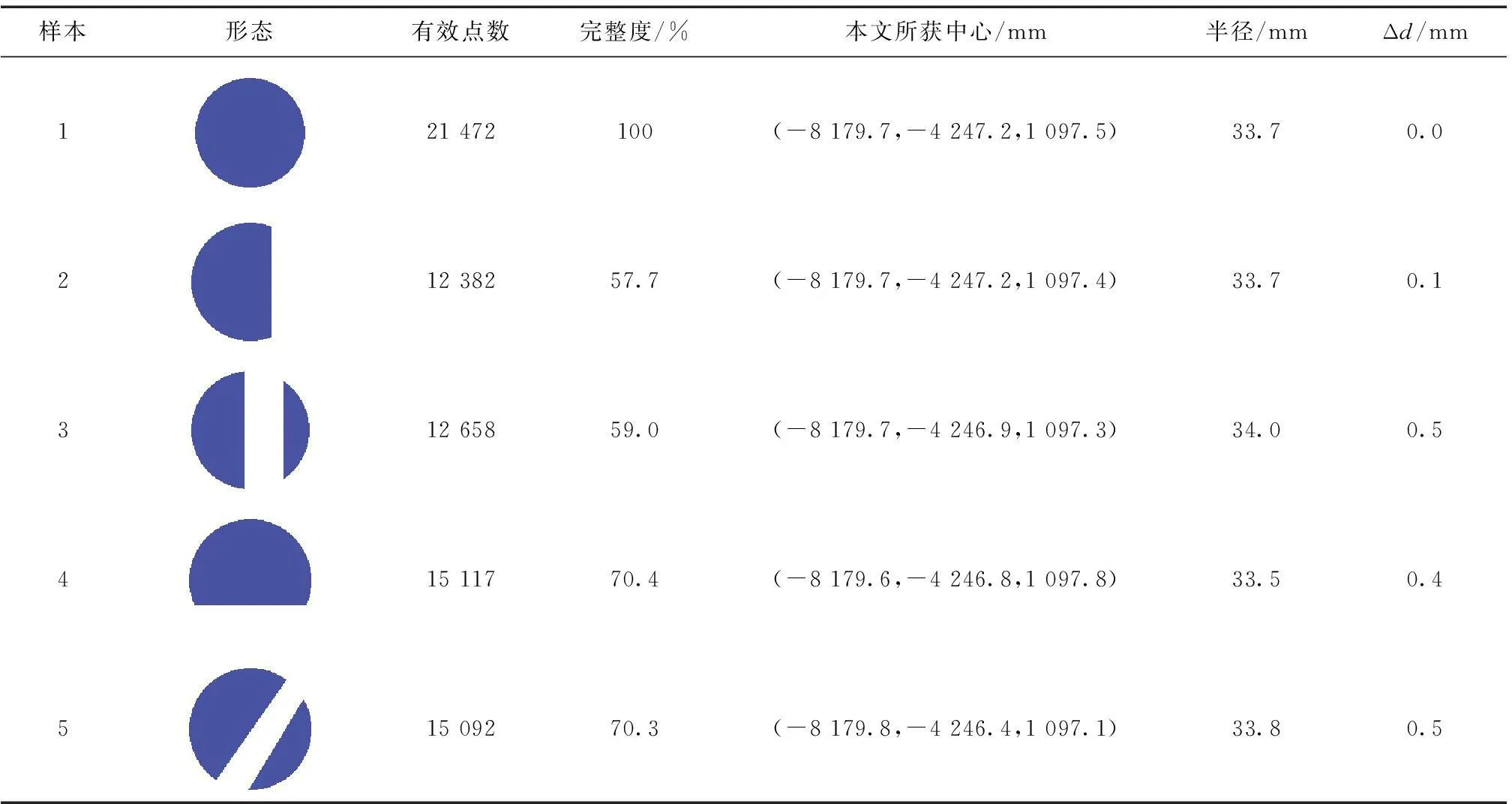
表1　不同残缺类型平面标靶定位结果

图4　不同残缺类型中缺失率对Δd的影响

5结束语

利用平面标靶边缘点的分布特性，采用具有抗差特性的RANSAC算法，通过设置两个阈值即能够有效提取出准确的标靶平面以及边缘点所在圆。该方法大大减小了拖尾点和数据缺失对平面标靶定位的干扰，提高平面标靶定位鲁棒性。

参考文献：

[1]曹先革,张随甲,司海燕,等.地面三维激光扫描点云数据精度影响因素及控制措施[J].测绘工程,2014,23(12):5-12.

[2]LICHIT D D,STEWART M P,TSAKIRI M,et al.

Benchmark Tests on a Three-dimensional Laser Scanning System[J].Geometrics’ Research Australasia,2000,72:1-23.

[3]陈西江,花向红，杨荣华，等.分带K均值聚类的平面标靶定位[J].武汉大学学报(信息科学版),2013(2):167-170.

[4]陈俊杰,闫伟涛.基于激光点云的平面标靶中心坐标提取方法研究[J].工程勘察,2013(8):53-57.

[5]许烨璋，王鑫森，郑德华，等.一种改进的RANSAC算法提取多模型圆弧特征点云[J].测绘工程，2015,24(1)：28-32.

[6]余鹏磊,于海洋，谢秋平，等.基于RANSAC算法的地铁隧道点云数据滤波[J].测绘工程,2014，23(8):28-31.

[7]魏英姿,刘晓莉.基于随机抽取一致性的稳健点云平面拟合[J].北京工业大学学报,2014(3):400-403.

[8]李孟迪，蒋胜平，王红平.基于随机抽样一致性算法的稳健点云平面拟合方法[J].测绘科学，2015，40(1)：102-106.

[9]仝红菊，李浩，赵海强，等.无人机航摄影像的RANSAC自动定向方法研究[J].测绘与空间地理信息，2015，38 (4)：50-52.

[10] 袁豹,岳东杰，赵元忆，等.基于稳健加权总体最小二乘的地面三维激光扫描球形标靶定位[J].勘察科学技术,2013(1):19-22.

[责任编辑：李铭娜]

A robust location method of incomplete planar target based on RANSACXUE

Xiaolu,LIN Huan

(School of Earth Science and Engineering,Hohai University,Nanjing 210098,China)

Abstract：In order to solve the problem of ghost points and target point missing caused by blocking,a robust location method of planar target based on RANSAC is presented.This paper applies RANSAC to fitting the target plane.Every single target point is located on the plane after ranging error correction.The edge points are extracted in the method of polar coordinate transformation.Then Givens transformation is used to simplify 3D circle fitting to 2D circle fitting with RANSAC.Two experiments are made to analyze the locating precision of different-integrity planar target.The experimental results demonstrate that the method presented in this paper can effectively solve the problem and improve the robustness of planar target location.

Key words：planar target location；ghost point；data missing；RANSAC；Givens transformation

中图分类号：P225.2

文献标识码：A

文章编号：1006-7949(2016)04-0051-04

作者简介：薛晓璐(1990-)，男，硕士研究生.

基金项目：国家自然科学基金资助项目(41301406;41201439);江苏省自然科学基金资助项目(BK20130829)

收稿日期：2015-01-20；修回日期：2015-06-16