有限总体基尼系数的统计推断

艾小青

(北京工业大学 a.经管学院；b.首都社会建设与社会管理协同创新中心，北京100124)



有限总体基尼系数的统计推断

艾小青a,b

(北京工业大学 a.经管学院；b.首都社会建设与社会管理协同创新中心，北京100124)

摘要：进行基尼系数的统计推断时，已有研究一般都设定总体是无限的。研究在有限总体随机抽样的现实背景下，如何利用样本数据对总体基尼系数进行估计及其评价。从总体基尼系数的内涵和定义出发，介绍了非参数估计和参数估计的方法，构造了相应的估计量，基于蒙特卡罗的模拟结果，论证和揭示了不同情况下估计量的性质，并论述了方法的适用性以及在实际应用中需要注意的问题。

关键词：有限总体；基尼系数；非参数估计；参数估计

一、引言

基尼系数是测度收入等社会经济变量不平等的重要指标，它的理论性质和实践结果是学术界和社会各界关注的热点。对于特定研究对象而言，可以理解为一个包含一定数量个体的总体，其基尼系数往往需要利用样本数据去估计，如何利用样本数据对总体基尼系数进行估计及其评价，这既是一个理论问题，也是重要的应用问题。

估计总体基尼系数有两种常见的方法：一是非参数法，也叫做直接估计法，即根据样本数据直接计算出样本基尼系数或者相关表达式，并作为总体基尼系数的估计；二是参数法，也叫做间接估计法，在总体收入分布函数的假定下，总体基尼系数可以由分布函数的相关参数得到，只需估计出相应的参数值就得到了对总体基尼系数估计。陈希孺认为，当对总体收入分布的形式有较大把握时，采用参数法有利于提高估计效率，当样本量较大时，采用非参数法比较稳妥，有可能的话可以同时使用两种方法并比较其结果[1]。Cowell指出，采用参数法估计总体基尼系数时，收入分布函数形式和参数估计方法的选择对结果会有影响[2]。

Davidson采用非参数法，给出了总体基尼系数的一个plug-in估计，并论证了估计量在大样本下的渐进正态性[3]。胡志军和龚志民模拟并提出了plug-in估计量在小样本下的近似正态性[4]。陈家鼎和陈奇志从洛伦茨曲线拟合出发，构造了总体基尼系数的估计量，并论证了估计量收敛于正态分布及其方差估计的强相合性[5]。戴平生从收入份额出发，推导出了样本基尼系数的不同计算式，并给出了方差估计的简便算法[6]。陈娟采用核密度估计法对收入分布函数进行了拟合，通过积分求解得到了基尼系数的估计结果[7]。杨耀武和杨澄宇采用自助法对样本基尼系数的标准误进行了估计，在此基础上得到了对总体基尼系数的区间估计[8]。

我们注意到，这些已有文献中专门针对有限总体基尼系数的统计推断的研究很少，它们往往借用了数学中无限总体的理论设定，忽略或者不考虑这样的现实背景，即样本数据通常是在有限总体进行随机抽样得到的。本文将基于有限总体的设定，对有限总体基尼系数的统计推断问题进行研究，在单元数为N的总体内进行样本量为n的不放回简单随机抽样，如何根据样本数据对总体基尼系数进行估计，估计量的抽样性质有哪些？在前人研究的基础上，本文一方面将基于有限总体基尼系数的内涵辨析，给出其非参数估计方法和超总体模型假定下的参数估计方法，另一方面将通过蒙特卡罗模拟对估计量的偏差、标准误等估计量性质进行揭示和检验，对不同估计方法以及不同样本量下的情形进行对比分析，并对各种方法在特定情况以及实际应用中应该注意的问题进行讨论。

二、理论基础

(一)基本定义

无限总体包含的个体数量是无限多个，个体的取值是随机变量的结果，而有限总体包含的个体数量是特定常数N，个体的取值是既定的。无限总体是数学概念上的一般化，现实中的特定总体事实上都是有限总体，如以某个国家或地区为总体，其包含的居民(个体)数量必然是有限的。统计推断则是在有限总体内进行抽样，然后利用样本数据去推断总体特征。设定在一个包含N个个体的有限总体(以下简称总体)内进行样本量为n的不放回简单随机抽样，抽样比f为n/N。总体单元不会被重复抽取，有效样本量即为n，本文暂不讨论其他复杂抽样下的情形。

目标变量以收入变量为例，其他社会经济变量的分析与之类似。总体单元i的收入为Xi,i=1,2,…,N，通常认为收入值不小于0。样本单元i的收入为xi,i=1,2,…,n，为了下文论述方便，样本单元不妨按收入的升序排列，则有x1≤x2,…,xn-1≤xn，并有样本单元i的收入秩(排序位置)的值即为i。

(二)总体基尼系数的辨析

给定总体的N个数据，其基尼系数的基本计算式在已有文献中常见两个版本，第一个计算式是：

第二个计算式是：

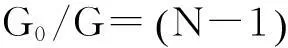
(三)总体基尼系数的估计

利用样本数据对总体未知特征进行估计，从抽样推断而言有两种方法，一是传统的直接估计，本质上是一种非参数估计；二是在超总体模型假定下的间接估计，本质上是一种参数估计。这两种方法对于总体基尼系数的估计同样适用：前者是对总体收入既定取值不做任何分布假定，直接构造样本基尼系数或者相关表达式，作为总体基尼系数的估计；后者是假定总体收入取值服从一定的分布函数(即超总体模型)，总体基尼系数与分布函数的某些参数有关，研究者需要利用样本数据估计出分布函数的未知参数，便得到了总体基尼系数的估计。还有其他一些方法可以理解为这两种方法的拓展。

非参数估计相对简单和明确，但样本基尼系数的抽样性质比较复杂，参数估计相对复杂和多变，要涉及到分布函数的假定和参数估计的策略，所得估计量的抽样性质取决于多种因素。下文将对两种方法下总体基尼系数的统计推断进行深入讨论。

三、总体基尼系数的参数估计

(一)估计量的构造

基于总体基尼系数G的计算式，样本基尼系数的计算式为：

(1)

该计算式与下列计算式都是等价的：

(2)

(3)

式(2)实质上是基尼系数的协方差表达式，式(3)也是从协方差表达式中推导出来的，Davidson(2009)提出的修正plug-in估计量实质上就是式(3)的表达式。

以样本基尼系数gn作为总体基尼系数G的估计量，当样本量n等于总体单元数N时，样本基尼系数即为总体基尼系数。

(二)估计量的性质

样本基尼系数的计算式比较复杂，在随机抽样下它的抽样性质很难直接通过数理推导得到，而蒙特卡罗模拟是一种处理复杂估计量的有效方法。这里我们利用R软件进行蒙特卡罗模拟，对样本基尼系数的期望、偏差、标准误等特征值，以及它的分布特征进行研究。

模拟的第一步是生成总体数据，总体单元数N设定为1 000，事实上当N趋于无穷大时有限总体也就成了无限总体。为保证结论的可信度，我们构造两个总体A和B进行考察，基于帕累托分布和对数正态分布的随机数产生总体单元的收入变量取值，并计算出总体基尼系数，GA为0.307 6，GB为0.488 7。然后再在总体内进行样本量为n的不放回简单随机抽样。为保证结果的稳健性模拟次数k为10万次，样本量设定为5、10、20、50、100、200、500不等，通过模拟结果考察估计量的性质。

表1　不同样本量下样本基尼系数的模拟结果

已有研究指出，样本基尼系数的偏差以及标准误的平方(即估计量方差)，一般都与样本量成反例，当样本量趋向无穷大时样本基尼系数渐进无偏且收敛于正态分布[2，5]。以上结论都默认理论总体是无限的，在有限总体中，以上结论应根据抽样比f做出相应调整：有限总体抽样下的样本基尼系数，其偏差和估计量方差都近似与(1-f)/n成比例，当抽样比f为1即总体都进行调查时，样本基尼系数的偏差和估计量方差都为0。

我们利用两个总体的模拟结果，对估计量偏差和方差与样本量的内在关系进行了估计：

各估计的决定系数都达到了0.9以上，两个总体下得到了基本一致性的结论，说明我们在有限总体下对样本基尼系数(估计量)性质的判断和调整是合理的，在特定总体和抽样机制下，它的偏差和方差的一般表达式为：

(4)

其中kb和kv为特定系数，取值大小取决于总体特征和抽样机制。随着样本量的增加，偏差和方差都将减小并趋于0。结果还显示，在不同情况下样本基尼系数的期望值总是要小于总体基尼系数，当样本量较小时，这种偏离程度更严重。由此可见，用数量较少的样本数据或者分组数据计算样本基尼系数并对其估计，将很可能造成结果的低估，这是需要特别小心的。

考察覆盖率与样本量的关系，显然随着样本量的增加覆盖率也随之增加。我们还考察了样本基尼系数在不同样本量下的分布特征，以总体A为例，样本量以5、10、20为例代表小样本，以50、100、200为例代表较大样本，样本基尼系数的分布如图1所示，可以发现在小样本时是右偏的，在较大样本是近似正态的。

图1　不同样本时样本基尼系数的分布

四、总体基尼系数的非参数估计

(一)估计量的构造

总体基尼系数非参数估计的核心是收入分布函数(即抽样术语中的超总体模型)的假定和估计，这种方法的优势在于当模型假定与实际相符并且参数估计准确时，总体基尼系数的估计精度较高。整个过程包括四步：一是假定收入分布函数；二是确定基尼系数与分布函数参数的关系；三是利用样本数据拟合分布函数，估计分布函数参数；四是利用分布函数参数的估计结果以及基尼系数与分布函数参数的已知关系，得到总体基尼系数的估计。

1.收入分布函数的假定。模型视角下的抽样推断，认为总体之上还存在超总体，总体取值不是既定的，而是超总体模型的随机生成。假定总体单元的收入取值独立同分布，其分布服从的概率密度函数为f(X)，分布函数为F(X)。现实中的收入分布通常都是单峰右偏的，应用最广泛的两种理论收入分布为对数正态和帕累托分布，一方面它们有着优良的数理性质，比如其对数线性变换的一致性，以及其洛伦茨曲线的不相交性等，另一方面国内外大量实证研究表明，这两种分布对现实收入数据的拟合性较好，这里以这两种分布为例进行介绍。

2.基尼系数与分布函数的关系。已知随机变量的概率密度函数f(X)或分布函数F(X)，其基尼系数的理论计算式为：

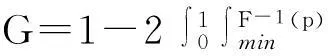
(5)

该计算式还可以转化为以下等价的表述：

(6)

(7)

(8)

以上计算看似复杂，但如果已知具体的分布函数形式，基尼系数的结果是分布函数参数的函数式，在特定分布下基尼系数与分布函数参数有着简单明确的关系。

在对数正态分布下，基尼系数为：

(9)

在帕累托分布下，基尼系数为：

(10)

可以看出，对数正态分布或帕累托分布的基尼系数只与其尺度参数有关，已知对数正态分布函数的参数σ，或者帕累托分布的参数α，就能直接求出基尼系数。这也意味着只要我们能估计出分布函数中相应的未知参数，就能估计出总体基尼系数。

3.分布函数拟合和参数估计。对于特定形式分布函数的拟合，实质上就是利用样本数据对分布函数中未知参数的估计。常用的参数估计方法有矩估计、极大似然估计和最小二乘估计等，很多时候不同方法下的估计结果是近似乃至一致的。

对数正态分布的位置参数μ和尺度参数σ的极大似然估计结果为：

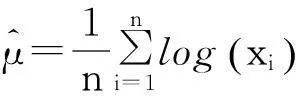
(11)

帕累托分布的位置参数θ和尺度参数α的矩估计结果为：

(12)

这两种分布下我们更关注尺度参数的估计结果，因为基尼系数值只与尺度参数有关。

4.总体基尼系数的估计。在特定分布函数(如对数正态分布和帕累托分布)的假定下我们已知了基尼系数与分布函数参数的关系，利用样本数据我们又估计出了分布函数中的未知参数，两者结合便得到了对总体基尼系数的估计。

把式(11)代入式(9)，得到对数正态分布下总体基尼系数的估计为：

(13)

把式(12)代入式(10)，得到帕累托分布下总体基尼系数的估计为：

(14)

(二)估计量的性质

很多研究强调样本数据对收入分布函数的拟合程度，事实上这并不是问题的关键，真正关键的是对总体收入分布的假定是否准确。比如假定总体收入分布形式更符合对数正态分布，但由于实际抽样调查中低收入人群的样本数较少，使得样本数据的收入分布形式更接近帕累托分布；如果强调样本数据的拟合度而选择了帕累托分布的形式，以此去估计总体基尼系数的结果，看似样本数据对收入分布的拟合度高，但估计结果可能很不准确。接下来我们通过统计模拟来进行验证，并揭示总体基尼系数参数估计下估计量的具体性质。

使用前文中的总体B数据，其收入分布比较接近对数正态分布。假定我们利用样本数据进行收入分布函数拟合时，一种是正确地选择对数正态分布的形式进行参数估计，并得到了总体基尼系数的估计结果，另一种是错误地选择了帕累托分布的形式并得到了估计结果。利用R软件进行10万次的蒙特卡罗模拟，样本量也同样设定为5、10、20、50、100、200、500不等，计算估计量的期望值、偏差和标准误等特征值，以及估计量与总体基尼系数的相对误差不超过10%的比例(覆盖率)，相关模拟结果如表2所示。

表2　不同样本量下总体基尼系数估计量的模拟结果

模拟结果给我们的启示有：一方面，一旦对总体收入分布形式的预判是错误的，利用样本数据对错误假定的分布函数进行拟合，即使拟合度很高，并不意味着对总体基尼系数的估计就准。上例中总体收入分布本身更符合对数正态形式，若用帕累托形式去拟合的话，会带来总体基尼系数结果的较大高估，甚至我们发现，样本量越大偏差还越大，覆盖率也越小(在较大样本时竟然近似为0)，出现了南辕北辙的灾难性后果。不少研究者在实证研究中，以样本数据对收入分布函数的拟合优度为依据，在得到较高拟合优度时就认为对总体基尼系数的估计也是准确的，这样的因果逻辑其实是不成立的。另一方面，当对总体收入分布形式的预判较为准确时，利用有限的样本数据，能得到对总体基尼系数相对较好的估计。上例中如果用对数正态形式去拟合收入分布并对总体基尼系数进行估计，从估计量性质来看，其偏差和方差都与样本量近似成反比，随着样本量增加是渐进无偏和近似正态的，从覆盖率来看，相比前文中用非参数方法对总体基尼系数估计时要更高，说明估计效果相对更好。

五、结论

本文讨论了针对特定的有限总体，如何利用随机抽样的样本数据去估计总体基尼系数。首先对总体基尼系数的内涵进行了辨析，指出如何合理地计算总体基尼系数；本文的前部分是总体基尼系数的非参数估计方法，介绍了如何利用样本基尼系数去估计总体基尼系数，并通过统计模拟揭示了样本基尼系数的偏差和方差等抽样性质，特别要注意样本基尼系数的期望值要小于总体基尼系数，当样本量较小时这种偏差较严重。现有研究常见在小样本或者分组数据时计算样本基尼系数去直接估计，很可能造成结果的低估。文中还给出了样本基尼系数的分布特征，揭示了在较大样本时的近似正态性。本文的后部分是总体基尼系数的参数估计方法，介绍了如何基于收入分布函数去估计总体基尼系数，文中以对数正态分布和帕累托分布为例，给出了总体基尼系数的估计量，通过统计模拟揭示了估计量的偏差和方差等抽样性质，特别论证了方法应用效果的关键并不是样本数据对收入分布函数的拟合程度，而是对总体收入分布形式假定是否准确，当总体收入分布假定正确时，估计量性质优良，然而当总体收入分布假定错误时，整个估计方法完全失效，后果是灾难性的。

在实际应用中，如何选择合适的方法去估计特定总体的基尼系数，需要综合考虑总体收入分布形式的预判、抽样机制以及样本量大小等因素。采用非参数估计方法是一种相对稳妥保守的做法，而当掌握了一定的历史数据或者相似总体数据等辅助信息，对总体收入分布形式的预判比较有把握时，或者当样本数据是来自严格的随机抽样，有理由相信通过样本数据拟合出的收入分布函数与总体比较一致时，可以考虑采用参数估计方法。当样本量特别小时，事实上任何一种估计都很难保证结果的准确性，可以综合采用不同的估计方法，同时要注意避免对真实值的低估。当样本量特别大时，样本与总体的基尼系数差别将很小，建议采用非参数估计方法。

本文只讨论了有限总体内简单随机抽样下基尼系数的统计推断问题，在复杂抽样下的相关问题有待进一步研究。

参考文献：

[1]陈希孺. 基尼系数及其估[J].统计研究，2004(8).

[2]Cowell A. Measuring Inequality[R/OL].Working Paper.Http:∥darp.lse.ac.uk/MI3, 2009.

[3]Davidson Russell. Reliable Inference for the Gini Index[J]. Journal of Econometrics, 2009，150(1).

[4]胡志军,龚志民. 收入基尼系数的统计推断[J].统计研究,2010(9).

[5]陈家鼎,陈奇志. 关于洛伦茨曲线和基尼系数的统计推断[J].应用数学学报, 2011(5).

[6]戴平生. 基尼系数的区间估计及其应用[J]. 统计研究,2013(1).

[7]陈娟. 基于收人分布的基尼系数非参数估算[J].数理统计与管理, 2013(7).

[8]杨耀武,杨澄宇. 中国基尼系数是否真的下降了？——基于微观数据的基尼系数区间估计[J].经济研究,2015(3).

(责任编辑：张治国)

Statistical Inference of Finite Population's Gini Index

AI Xiao-qinga,b

(a.School of Economics & Management； b. Collaborative Innovation Center of Beijing Society-Building & Social Governance, Beijing University of Technology, Beijing 100124, China)

Abstract:The population is generally set to be infinite theoretically in the study of statistical inference of Gini index, this paper studies the situation under the sampling in the real finite population. Based on the connotation and definition of population's Gini index, the paper analysis two methods of estimations named as non-parameter estimation and parameter estimation, then derives the corresponding estimators, demonstrates and reveals the properties of different estimators by Monte Carlo simulation. The paper specifically discusses the method's applicability and the issues that require attention in the practical use.

Key words:finite population; Gini index; non-parameter estimation; parameter estimation

中图分类号：C811∶F126.2

文献标志码：A

文章编号：1007-3116(2016)03-0003-06

作者简介：艾小青，男，湖南邵阳人，统计学博士，副教授，硕士生导师，研究方向：抽样调查及统计指数。

基金项目：国家自然科学基金资助项目《关于涵盖误差的我国周期性普查数据质量评估方法：理论与应用研究》(71301033)；北京市社科基金基地项目《基于系统动力学的京津冀现代制造业协同发展研究》(14JDJGC040)；北京工业大学日新人才项目(011000514115005)

收稿日期：2015-09-18；修复日期：2015-12-10

【统计理论与方法】