FLAC3D流固耦合渗流模型探讨

邓思远， 杨其新，*， 蒋雅君， 陈　浩

(1． 西南交通大学土木工程学院交通隧道工程教育部重点实验室， 四川 成都　610031；

2． 江苏省交通规划设计院股份有限公司轨道所， 江苏 南京　210014)



FLAC3D流固耦合渗流模型探讨

邓思远1， 杨其新1，*， 蒋雅君1， 陈浩2

(1． 西南交通大学土木工程学院交通隧道工程教育部重点实验室， 四川 成都610031；

2． 江苏省交通规划设计院股份有限公司轨道所， 江苏 南京210014)

摘要：FLAC3D有限元软件内置4种渗流模型，直接决定计算结果正确与否。渗流场在三维空间中分布复杂，难以根据计算公式定量选用何种模型，不同文献渗流模型选择标准也不相同。为了找到简单、快速、合理的选择方法，有必要对4种渗流模型进行受力分析。以一100 m×100 m×10 m各项同性弹性立方体为例，基于4种渗流模型设计4种工况。通过对比和分析各工况下总应力和孔隙水压分布情况，主要结论如下： 1)模型A、模型C外荷载均由土颗粒骨架承担，其余2种模型流体也参与受力； 2)流体分担外荷载的比例与刚度系数和时间有关； 3)FLAC3D流固耦合过程正是通过调整刚度比、打开和关闭力学-流体进程来实现的。目前我国流固耦合计算基本基于FLAC3D有限元软件，文中结论适用于基础、隧道、基坑等工程，可供相关从业人士借鉴参考。

关键词：流固耦合； 渗流模式； FLAC3D； 岩土工程

0引言

岩土工程施工阶段引排水改变地下水分布，令土体有效应力重新分布，有效应力场反过来又影响地下水运动，这种应力场和渗流场相互作用的现象被称为流固耦合[1]。20世纪中期，比奥按弹性力学理论推导出方程组，由于求解困难，当时未引起重视。近些年来，相关研究成果显著。一方面，专家学者研制出能模拟流固耦合的模型试验系统。比如： 文献[2]通过模型试验得到海底隧道施工中围岩力学行为和渗流场变化规律；文献[3]对比了模型试验和数值计算之间的差异。另一方面，基于流固耦合的数值计算如火如荼。比如： 文献[4]将流固耦合用于双圆异性断面盾构隧道施工分析；文献[5]研究了基坑开挖时支护变形和孔隙水压的分布。目前，研究正向着裂隙介质非均匀流、非饱和渗流以及多场耦合方向发展[6-7]。

虽然成果丰硕，但在流固耦合基础应用方面还存在一些问题。我国流固耦合数值模拟主要基于FLAC3D平台，软件内置4种渗流模型。基坑、隧道开挖是一个复杂、循环往复的过程，既存在土体开挖卸荷，也存在引排水改变渗流场，难以根据用户手册选择适合的模型，很多文献选择模型的标准也不尽相同。文献[8]模拟地铁开挖时，先计算应力场，再进行流固耦合或渗流计算；文献[9]模拟基坑开挖时，先等渗流场稳定后，再进行应力计算。上述处理方法均有一定道理，到目前尚未有文献针对4种模型受力特点进行详实论证。为了解4种模型的受力本质，确保计算结果能指导工程，本文将以一各项同性弹性立方体为例，对各模型的受力特点进行分析。

1流固耦合概述

1.1相关理论

如图1所示，取一微元体，建立基本微分平衡方程：

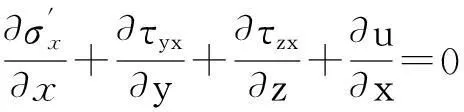
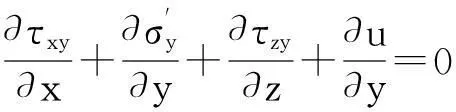
(1)

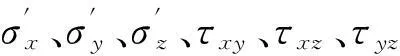
图1　微元体受力示意图

1.2计算原理

FLAC3D计算过程简化如图2所示，左边表示应力场计算的过程，右边表示考虑渗流场后的新增步骤。表1为FLAC3D用户手册渗流模型选择标准，主要是根据特征时间和扰动类型确定的。

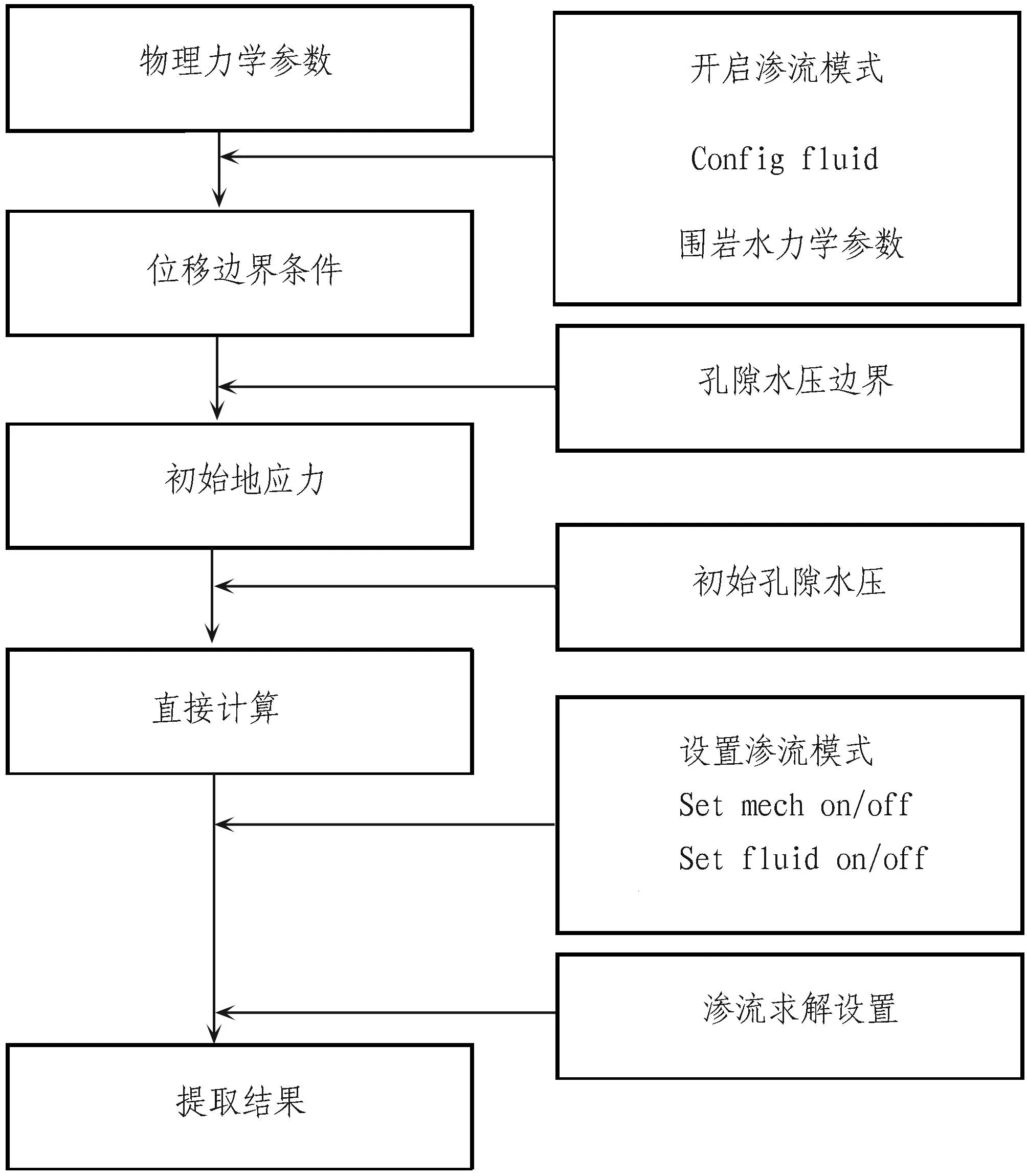
图2　FLAC3D建模流程

软件根据运动方程、平衡方程、本构方程、相容方程以及边界条件进行求解[1]。

1)运动方程是由达西定律v=k·i推导而来，渗流速度

(2)

2)平衡方程是在小变形情况下，单位时间内微元体含水量变化值等于流入量与流出量之差：

(3)

式中:qυ为微元体流体流入量；ζ为单元流体体积变化值。

3)本文只针对饱和土体渗流模型，其本构方程为

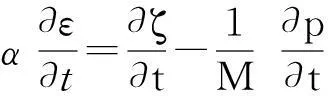
(4)

式中：M为比奥模量；α为比奥系数；ε为应力场引起的体积应变。

4)应变率和速度梯度应满足相容方程：

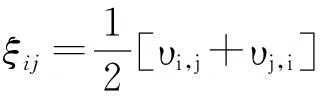
。　(5)

1.3工程应用难点

FLAC3D英文手册给出渗流特征时间的计算公式，特征时间可通过式(6)—(8)[1]计算。

Lc=Vf/Af。

(6)

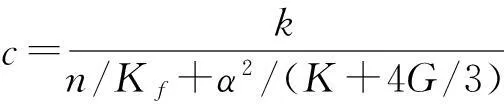
(7)

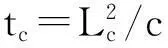
(8)

式中： Lc为特征长度； Vf为渗流区域体积； Af为渗流区域表面积； tc为特征时间； k为FLAC3D渗透系数； n为孔隙率； Kf为流体体积模量； K为围岩排水条件体积模量； G为围岩排水条件剪切模量； α为比奥系数。

对于简单的一维渗流，容易得到特征长度和特征时间。如图3所示，现有一厚度为20m的饱和土层，底部为一不透水刚体，顶部作用均布荷载，水通过顶部排除，所以特征长度取土体厚度，即20m[12]；但在实际工程中，地下水的运动是三维的，难以确定特征时间和渗流模型。

太沙基把土的渗透固结简化为一个装满水的容器，容器上方有一开小孔的活塞，活塞下面用一根弹簧支撑。当荷载刚作用上去时，小孔中的水来不及排出，由水和弹簧共同承担荷载。当荷载作用长时间后，多余的水分排出，弹簧承担全部的荷载[13]。本文的研究思路是将土的渗流固结过程分段，建立各段与渗流模型之间的对应关系。例如对应排水固结阶段的渗流模型，理论上不会出现超孔隙水压。

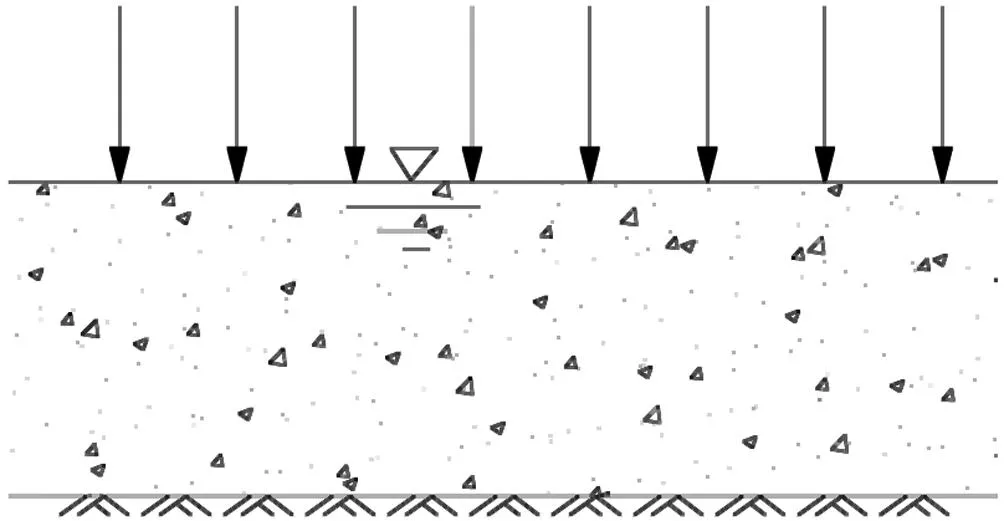
图3　一维渗流算例

2模型设计

2.1模型试算

为了保证建模正确性，现进行模型试算。根据相关文献[3、14]，建立青岛胶州湾海底隧道流固耦合模型，如图4所示。由于部分参数(开挖时间、加固区尺寸)未在文献中找到，所以未知参数按经验取值。

图4　青岛胶州湾海底隧道模型

图5与图6为试算结果同原文的对比，结果存在一定的差异，主要是由于部分参数取值不同而引起的，但围岩竖向位移、内力均在同一数量级，变形收敛趋势是相同的。文献[3]还就数值计算结果同模型试验进行了对比，若不考虑裂隙水、围岩产状等因素，数值解和试验结果相当接近。

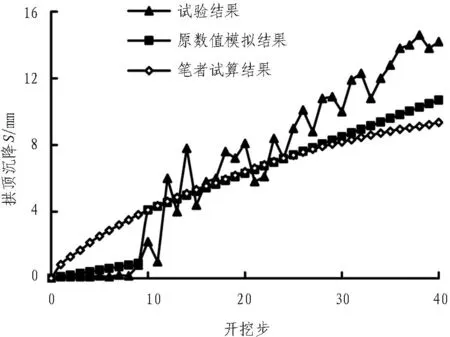
图5　青岛胶州湾海底隧道试算结果

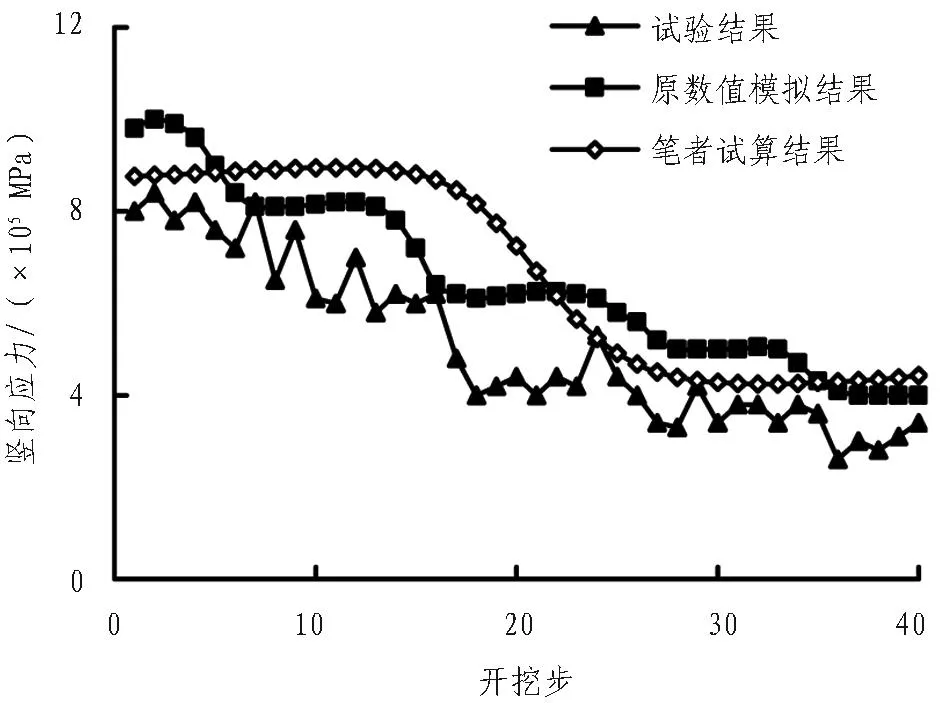
图6　青岛胶州湾海底隧道试算结果

流固耦合计算费时，可以沿隧道中心面取一半建模，以加快计算速度，如图7所示。需要注意隧道中心面处孔隙水压力边界条件，通常设置为不透水边界，即孔隙水压是可变化的。

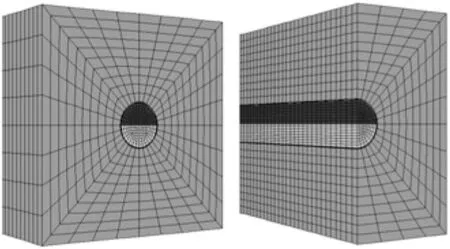
图7　圆形隧道模型

2.2参数设计

本文的目的是为了分析4种渗流模式的受力本质，从而与实际工程建立联系，就如同钢桁梁桥总体受力虽然复杂，但每根钢杆依然准守基本的力学公式。本文以简单模型为例，更便于分析说明，所得结论，亦适用于复杂模型。

现设一100m×100m×10m立方体，水位高出地面10m。初始平衡以后，在顶部施加一竖向均布荷载q，大小为500kPa。在模型中心从上到下依次取点A—J10个监测点，监测其初始竖向总应力σ0、初始孔隙水压p0、加载后竖向总应力σ1、加载后孔隙水压p1。模型示意图见图8。

这是卒中后吞咽障碍患者营养管理模式的创新与医院发展战略一致的大背景之一。在项目中，多学科团队的协作，在郑大一附院也有着深厚的基础和浓郁的氛围。据刘章锁介绍，多学科管理团队在医院落地已有7年之久。“目前，门诊有28个多学科会诊团队。”

图8　模型示意图

为了防止模型屈服破坏，力学模式采用理想弹性模型，渗流模式采用各项同性渗流模型，参数取整，详见表2和表3。

表2　模型物理力学参数

表3　模型水力学参数

2.3工况设计

FLAC3D内置4种渗流模型，各模型力学进程、流体进程、流体体积模量Kf有所差别。通常流体不考虑压缩变形，土体的变形是由于流体迁移和土颗粒骨架空隙间的变形。FLAC3D将流体考虑成可压缩变形的，相关资料请参考FLAC3D用户手册。现根据不同进程和流体模量设置4种工况，见表4 。

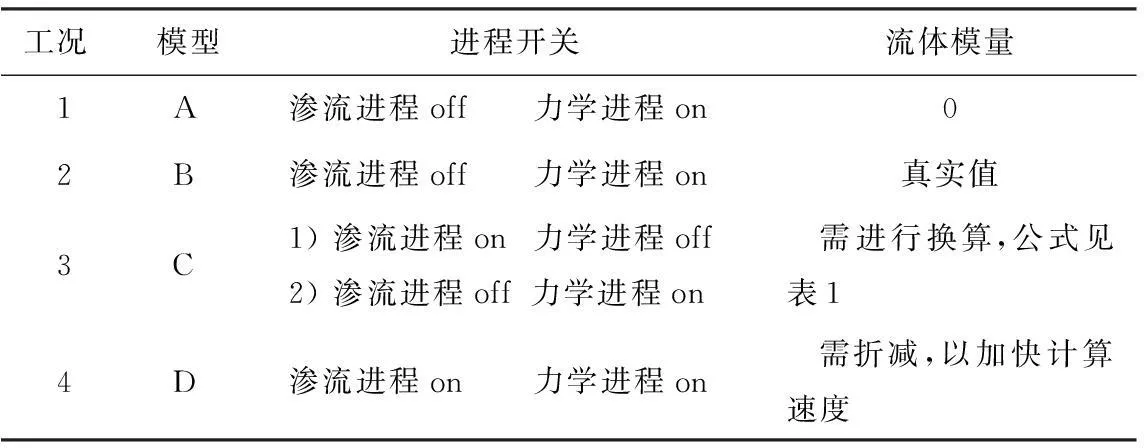
表4　计算工况

3计算结果及分析

3.1工况1计算结果

工况1是在初始平衡后，顶部施加荷载500 kPa，维持力学进程开启和流体进程关闭，流体体积模量Kf为0，计算至平衡。工况1应力竖向分布曲线如图9所示。由图9可知： 曲线p0和曲线p1重合，说明加载后孔隙水压不变；有效应力增大约为500 kPa，即外界施加的荷载由土颗粒骨架承担，水不分担压力。

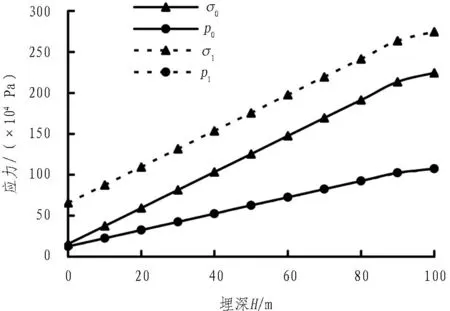
图9　工况1应力竖向分布曲线

3.2工况2计算结果

工况2同工况1类似，维持力学进程开启和流体进程关闭。与工况1不同的是，此时需要将流体体积模量Kf设置为真实值。工况2应力竖向分布曲线见图10。由图10可知，外界荷载一部分由土颗粒骨架传递，一部分由流体承担。

在试算时还发现流体承担的荷载大小，同流体和固体的刚度比Rk有关。新增1组对比模型，将流体的体积模量降低10倍，以分析刚度比Rk对结果的影响。刚度比

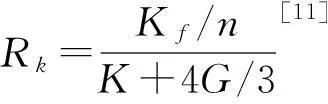
(9)

式中：Kf为流体体积模量;n为孔隙率;K为固体体积模量;G为固体切变模量。

图10　工况2应力竖向分布曲线

图10中曲线σ1(柔性)和曲线σ1(刚性)重合。通过对比发现，流体分担外荷载比例同刚度比Rk成正比。因此可作出一个假设：土颗粒和流体分担外力原理类似图11。刚度比Rk就是2根弹簧的弹性系数k比值，当刚度比Rk等于0时，代表流体的弹簧弹性系数k等于0，外荷载全由另一根弹簧——土颗粒骨架全部承担。工况1正是刚度Rk等于0的特殊状态。

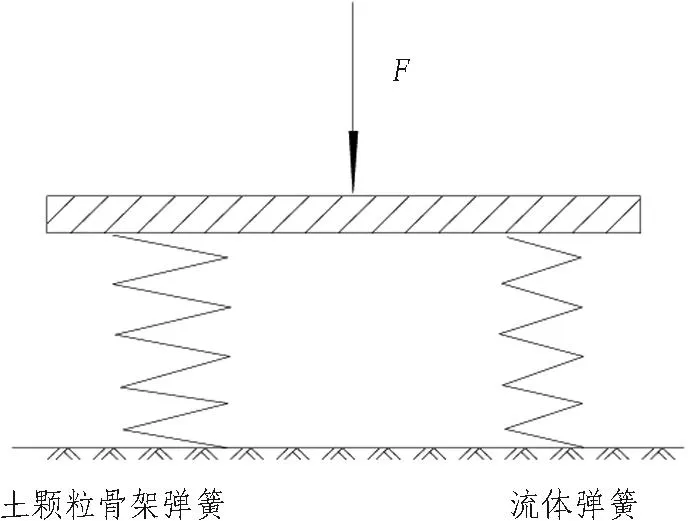
图11　流体-固体刚度比示意图

3.3工况3计算结果

由于工况3是模拟孔隙水压变化引起的内力重分布，所以初始平衡之后，不再施加500 kPa荷载，而是将顶部孔隙水压提高500 kPa。另外，工况3和工况4需要设置时间，这里将时间取一个大值，使模型渗流运动场趋于稳定。

工况3计算过程可视作2个独立的步骤： 第1步是孔隙水压变化引起渗流场重分布，有效应力场不发生变化；第2步是渗流场重分布后，有效应力场变化发生。工况3应力竖向分布曲线见图12。图12中曲线p1(M off/F on)和曲线p1(M on/F off)重合，说明有效引力场改变并未引起孔隙水压力重分布。结果再次证明本文3.2节假设模型的正确性——Rk=0时，流体不参与受力的。

M代表力学进程；F代表渗流进程。

图12工况3应力竖向分布曲线

Fig. 12Distribution curves of vertical stress in Case 3

在分析实际工程时，孔隙水压的改变通常是人为控制的。比如开挖隧道时，将开挖后的单元孔隙水压设置为0，围岩周围单元的孔隙水压会根据已知孔隙水压力边界条件重新分布。

3.4工况4计算结果

工况4中流体参与分担外荷载，并且分担的数值与时间有关。现在设置2组对比模型，计算时间分别为6 000 s和60 000 s，其余参数相同。工况4应力竖向分布曲线见图13。图13中曲线σ1(6 000 s)和曲线σ1(60 000 s)重合，随着时间的的增加，超孔隙水压消散，有效应力增大。结合图9和图10，工况4可以近似看作工况1和工况2的中间状态。当计算时间足够长时，结果近似于工况1；当计算时间十分短时，工况4的结果近似于工况2结果。

由此得到这样一个结论——模型D适用于任何情况。分析透水性好的砂土排水固结或是透水性差的黏土不排水固结，都可以选用模型D，只要时间按真实情况取值即可；但流固耦合相当费时，所以模型D只是“理论上”适用于各种情况。根据大量的试算还发现，不仅合理的渗流模型能节约时间，采取合理的网格形状，避免单元尺寸过小，亦能减小单元数量和增大时间步time-step，从而缩短时间。

图13　工况4应力竖向分布曲线

4结论与建议

1)模型A、模型C外荷载全部由土颗粒骨架承担，模型B、模型D流体也分担外荷载。

2)流体分担外荷载比例与刚度比Rk成正比，模型D流体分担比例还与作用时间有关。

如透水砂层在外荷载作用下长期变形，宜选用模型A；透水不良黏土层突然受外力作用，宜选用模型B；抽水引起基础变形，宜选用模型C；黏土层排水固结过程可采用模型D。如果将土的渗透固结过程看作是用手在压一个装满水的容器的话[13]，那么FLAC3D中4个模式对应关系参考图14(笔者注： 图11与图14的模型是在大量试算基础上，为了便于理解而假设的定性模型)。

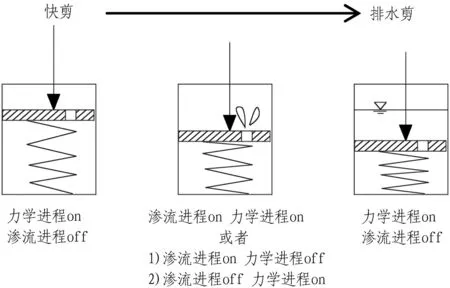
图14　对应关系示意图

3)FLAC3D流固耦合正是通过调整刚度比Rk，打开和关闭力学-流体进程来实现的；但是由于流固耦合十分费时，一般通过调整流体体积模量Kf或比奥模量M减少计算时间。此外，手册还指出计算渗流稳定状态时，流体比奥模量要满足M>αLzρωg/n[1]，以确保流体自由面稳定。相关理论还待作进一步研究。

参考文献(References)：

[1]Itasca Consulting Group Minneapolis. Fast language analysis of continua in 3 Dimensions[EB/OL].Version 3.0, User’s manual.Minneapolis: Itasca Consulting Group,2005.

[2]李术才,宋曙光,李利平,等. 海底隧道流固耦合模型试验系统的研制及应用[J]. 岩石力学与工程学报,2013,32(5): 883-890.(LI Shucai, SONG Shuguang, LI Liping, et al. Development on subsea tunnel model test system for solid-fluid coupling and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2013,32(5): 883-890. (in Chinese))

[3]蔚立元,李术才,徐帮树,等. 水下隧道流固耦合模型试验与数值分析[J]. 岩石力学与工程学报,2011,30(7): 1467-1474.(YU Liyuan, LI Shucai, XU Bangshu, et al. Study of solid-fluid coupling model test and numerical analysis of underwater tunnels [J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(7): 1467-1474. (in Chinese))

[4]陈宇,朱继文. 双圆盾构隧道的流固耦合分析[J]. 地下空间与工程学报,2010,6(1): 21-27.(CHEN Yu, ZHU Jiwen. Coupled fluid-mechanical analysis of DOT shield tunnel [J]. Chinese Journal of Underground Space and Engineering,2010,6(1): 21-27. (in Chinese))

[5]冯怀平，张伏光，岳祖润. 考虑流固耦合作用的深基坑有限元分析[J]. 地下空间与工程学报,2012,8(2): 286-291.(FENG Huaiping, ZHANG Fuguang, YUE Zurun. Numerical analysis of excavation considering the coupling of seepage field and stress field [J]. Chinese Journal of Underground Space and Engineering,2012,8(2): 286-291.(in Chinese))

[6]刘泉声,刘学伟. 多场耦合作用下岩体裂隙扩展演化关键问题研究[J]. 岩土力学,2014,35(2): 305-320.(LIU Quansheng, LIU Xuewei. Research on critical problem for fracture network propagation and evolution with multifield coupling of fractured rock mass [J]. Rock and Soil Mechanics,2014,35(2): 305-320. (in Chinese))

[7]谢东海,冯涛,赵延林,等. 裂隙煤岩体的流固耦合精细模型[J]. 中南大学学报(自然科学版),2013,44(5): 2014-2021.(XIE Donghai, FENG Tao, ZHAO Yanlin,et al. Fluid-solid coupling detailed model of rock-coal mass [J]. Journal of Central South University(Science and Technology),2013,44(5): 2014-2021.(in Chinese))

[8]陈育民,徐鼎平. FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社,2013. (CHEN Yumin, XU Dingping. FLAC/FLAC3D basis and engineering instance[M]. Beijing: China Water & Power Press, 2013. (in Chinese))

[9]彭文斌. FLAC3D实用教程[M]. 北京: 机械工业出版社,2008. (PENG Wenbin. FLAC3D practical tutorial [M]. Beijing: China Machine Press, 2008.(in Chinese))

[10]李广信. 高等土力学[M]. 北京: 清华大学出版社,2004. (LI Guangxin. Advanced soil mechanics [M]. Beijing: Tsinghua University Press, 2004.(in Chinese))

[11]王光钦. 弹性力学[M]. 北京: 中国铁道出版社,2008. (WANG Guangqin. Elastic mechanics [M]. Beijing: China Railway Publishing House, 2008. (in Chinese))

[12]刘波,韩彦辉. FLAC3D原理实例与运用指南[M]. 北京: 人民交通出版社,2005.(LIU Bo, HAN Yanhui. FLAC3D principle examples and application guide[M]. Beijing: China Communications Press, 2005. (in Chinese))

[13]刘成宇. 土力学[M]. 北京: 中国铁道出版社,2002. (LIU Chengyu. Soil mechanics [M]. Beijing: China Railway Publishing House, 2002. (in Chinese))

[14]马栋,谭忠盛. 青岛胶州湾海底隧道施工及机械配套技术[J]. 中国工程科学,2009,11(7): 45-52.(MA Dong, TAN Zhongsheng. Key tunneling technology and configuring big machines in Qingdao Jiaozhouwan subsea tunnel [J].Engineering Science,2009,11(7): 45-52. (in Chinese))

Discussion on Seepage Model Based on FLAC3D Solid-fluid Coupling

DENG Siyuan1, YANG Qixin1，*, JIANG Yajun1, CHEN Hao2

(1.KeyLaboratoryofTransportationTunnelEngineeringofMinistryofEducation,SchoolofCivilEngineering,SouthwestJiaotongUniversity,Chengdu610031,Sichuan,China; 2.TrackwayInstitute,JiangsuProvincialCommunicationsPlanningandDesignInstituteCo.,Ltd.,Nanjing210014,Jiangsu，China)

Abstract:There are 4 seepage models in the FLAC3D finite element software; it is decided by selecting proper seepage models whether the result of numerical calculation is right or not. The seepage field distribution in three-dimensional space is complicate; as a result, it is difficult to decide a quantitative yardstick. There are different selection methods in different references. It is necessary to make stress analysis on the 4 seepage models, so as to choose a simple, rapid and rational model selection method. Four construction cases based on the 4 seepage models are designed, with a 100 m×100 m×10 m isotropic elastic cube as an example. The total stresses and seepage field distributions of the 4 construction cases are compared. The conclusions drawn are as follows: 1) For model A and model C, the soil skeleton carries all loads; for other 2 models， the fluid carries partial load too. 2) The load sharing ratio of fluid is based on the stiffness ratio and time. The solid-fluid coupling process in FLAC3D is realized by adjusting the stiffness ratio and switching mechanics-fluid process. So far, the calculation of solid-fluid coupling is almost based on FLAC3D in China. The conclusions can be applied to foundation engineering and underground engineering, and the paper can provide reference for similar projects.

Keywords:solid-fluid coupling; seepage model; FLAC3D; geotechnical engineering

中图分类号：U 45

文献标志码：A

文章编号：1672-741X(2016)02-0179-07

DOI:10.3973/j.issn.1672-741X.2016.02.009

作者简介：第一 邓思远(1990—)，男，四川宜宾人，西南交通大学桥梁与隧道专业在读硕士，主要研究方向为隧道及地下工程设计和施工技术。E-mail: dengsiyuan_2715@126.com。*通讯作者： 杨其新，E-mail: yangqixin113@163.com。

基金项目：四川省交通科技项目计划任务(2012C14-1)； 中央高校基本科研业务费专项资金资助(2682014CX065)

收稿日期：2015-11-15; 修回日期: 2015-11-28