星际探测太阳帆行星和太阳借力轨道全局优化*

钱　航，郑建华，李明涛，李　晖，高　东，于锡峥

(1.中国科学院 复杂航天系统电子信息技术重点实验室， 北京　100190；

2.中国科学院 空间天气学国家重点实验室， 北京　100190； 3.中国科学院大学， 北京　100190)



星际探测太阳帆行星和太阳借力轨道全局优化*

钱航1,3，郑建华1，李明涛1，李晖2，高东1，于锡峥1

(1.中国科学院 复杂航天系统电子信息技术重点实验室， 北京100190；

2.中国科学院 空间天气学国家重点实验室， 北京100190； 3.中国科学院大学， 北京100190)

摘要：以太阳帆在20年内飞行至距离太阳200 AU以远进行星际探测为目标，研究太阳帆通过行星借力和太阳借力的轨道全局优化问题。建立太阳帆时间最优转移轨道数学模型，分析行星借力和太阳借力的约束条件，并用这些约束条件构造目标函数，从而将轨道优化的四点边值问题转化为求解无约束条件下的多变量优化问题。通过选取合理的约束权重，采用遗传算法获得大范围的粗略解，代入到序列二次规划算法中获得高精度解。仿真结果表明，虽然太阳帆通过太阳借力已获得相当大的加速度，但加上木星借力仍然可以节省相当多的飞行时间。提出的轨道优化思路，可以为太阳系逃逸任务轨道初步设计提供参考。

关键词：星际探测；太阳帆；引力辅助；太阳光压辅助；轨道全局优化

外日球层以及星际空间是人类从未直接探索过的崭新领域，蕴含着许多重大科学发现的无限可能。迄今为止，国际上还没有一个专门设计的飞船计划对其展开综合性的就位与遥感探测。作为国际上首个为飞出日球层探索人类从未触及且知之甚少的星际空间而专门设计的飞船探测计划，中科院空间中心提出的星际快车(Interstellar Express)——“神梭”探测计划将开展概念研究，旨在设计一种能在20年内穿过日球层边界到达200AU(天文单位，1AU=1.495 978 70×1011m，表示地球到太阳的平均距离)以外星际空间的飞船方案，实现对外日球层和星际空间的等离子体、中性成分、尘埃、磁场、高能粒子、宇宙线和太阳系外红外辐射等信息的首次综合性就位及遥感探测，从而研究日球层内外的物质分布特性、邻近太阳系星际介质的性质、动力学特征及演化规律，揭示日球层与星际介质的相互作用过程及相互影响机制，促进对外日球层、邻近星际空间以及二者之间耦合过程的深入认识。

“神梭”探测计划的首要技术挑战就是设计一种经济可行的推进技术方案。现有四种先进星际航行推进技术：放射性同位素电推进(Radioisotope Electric Propulsion, REP)、核电推进(Nuclear-Electric Propulsion, NEP)、太阳帆推进(Solar Sail Propulsion, SSP)以及引力辅助推进(Gravity Assist Propulsion, GAP，即行星借力)。其中，太阳帆航天器虽然受到的太阳光压力很小，但持续加速可使太阳帆航天器在长时间后获得相当可观的速度，并且利用太阳帆可以实现传统航天器无法实现的非开普勒轨道，因而备受重视。

在太阳帆借力飞行和轨道优化方面，意大利比萨大学学者Quarta和Mengali根据非理想太阳帆的最优控制律设计了通过一次金星借力与水星交会的最小时间转移轨道[1]。Dachwald基于进化神经元算法研究了关于理想和非理想太阳帆的最优逃逸太阳系轨道，并以太阳帆最大耐热温度而不是以最小近日距离为优化约束[2]。Leipold总结了NASA冰火项目任务，提出高性能太阳帆采用单次或双次太阳光压辅助可以更快地飞往冥王星甚至更远目标，并认为无须进行引力辅助[3]。Matloff在给NASA报告中提出了在0.2 AU近日点的双曲轨道展开太阳帆、在椭圆轨道的近日点0.2AU展开太阳帆和木星借力这三种可能的近星际太阳帆探测方案设想，但没有给出具体任务轨道设计[4]。Vulpetti首次提出了三维角动量翻转太阳帆日心逃逸轨道设计方法[5]。

针对太阳系行星近似共面特点，太阳帆逃逸太阳系任务基于平面二体模型，对从地球出发在20年内通过行星借力和太阳借力获得巨大加速后到达距离太阳200 AU以远的轨道做初步设计。该问题需要考虑行星借力时太阳帆与行星位置约束，以及太阳借力时不得小于最小近日距离约束，和终端200 AU约束，属于复杂四点边值问题，用传统方法求解存在难以收敛、对初值敏感或计算速度慢等缺点。针对这一问题，可转化为无约束的优化问题，并引入相关算法进行求解。

1理想太阳帆时间最优转移轨道

给出太阳帆运动方程的极坐标形式，轨道半径为r，轨道相角为θ，径向速度是vr，横向速度为vθ，那么太阳帆在日心黄道J2000坐标系中平面轨道运动方程[6-9]为：

(1)

(2)

(3)

(4)

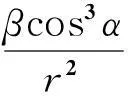
由于太阳帆不消耗燃料，唯一优化指标是飞行时间，故目标函数为：

(5)

构造该系统的哈密顿函数。

(6)

其中：λ=[λ1λ2λ3λ4]T为协态矢量。

(7)

(8)

(9)

(10)

根据庞德里亚金极小值原理，最优控制输入u*≡α*使哈密顿函数H最小。

(11)

其中：x*和λ*分别表示最优状态和最优协态矢量。最优方向角α*可以通过∂H/∂α=0得到。[10]

(12)

由协态方程(7)～(10)和式(12)可以看出，最优控制输入可由协态变量初值完全确定。

2借力与优化模型

2.1行星借力

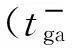
(13)

设vbody为行星在日心黄道惯性坐标系中的速度，在太阳帆飞越行星前后，相对行星的速度分别为：

(14)

(15)

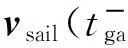
(16)

在飞越前后，太阳帆相对于行星的速度大小满足：

(17)

则当进行引力辅助时约束为：

(18)

(19)

引力辅助通过将相对速度矢量旋转δ角度，可以张成锥形空间，使得轨道能量增加或减少(相对速度大小不变)。对于平面行星借力问题，可以将相对速度δ角度张成扇形空间处理。计算得到标称转角δ，优化转角系数s，使得相对速度在扇形空间内(实际转角为转角系数s与标称转角δ乘积，-1≤s≤1)。

2.2太阳借力

太阳借力，又称为太阳光压辅助，是太阳帆独有的动力学特性。根据太阳光压加速度的计算公式(3)和式(4)，太阳帆获得的光压加速度与帆日距离平方成反比。对于星际飞行，从地球出发后先向内飞靠近太阳，获得巨大速度后逃逸出太阳系。考虑到材料的耐热性，太阳帆距离太阳限制在规定的距离以外。

rsail≥rmin

(20)

(21)

2.3全局优化

太阳帆转移轨道的初始条件为

(22)

终端约束条件为

(23)

其中：t0，tf分别为出发时刻和到达时刻；r0，rf分别为地球轨道半径和最远飞行距离。要求太阳帆初始相位角与地球相位角相同θ(t0)=θ0，对终端时刻相位角没有要求θ(tf)=free。

(24)

由式(8)可知，终端时刻并没有对相位角进行约束，则在时间区间[tga,tf]内，相位角的协态变量满足λ2=0。由式(8)和式(24)可以看出，在行星借力前的飞行时间区间[t0,tga]内，相位角的协态变量同样满足λ2=0，即整个飞行区间[t0,tf]内λ2=0，这样就可以减少两个优化变量，使得优化计算过程更顺利进行。

采用行星借力和太阳借力的太阳帆飞往太阳系边缘的任务轨道在行星借力处分为两段，行星借力认为是瞬间完成，相当于获得速度增量。而行星借力和太阳借力的先后顺序以及行星借力高度则是优化结果。

行星借力时要求太阳帆和借力天体的日心位置相同，即

rsail(tga)=rbody(tga)

(25)

同时，考虑到太阳帆飞越行星时必须有距离行星表面的安全高度hmin，这里规定为500 km，则

(26)

其中：Rbody为行星的半径。该约束为硬约束，构造约束函数方法同式(21)。

为使优化更容易，将行星借力约束和太阳借力约束转化在目标函数中，则太阳帆最优控制的目标函数为：

(27)

将协态变量初值作为寻优变量，从而太阳借力和行星借力组合的太阳帆转移轨道优化问题转化为一个无约束多变量优化问题，寻优参数为：

Y=[t0t1tfsλ11λ13λ14λ21λ23λ24]T

(28)

其中：t0为太阳帆从地球出发所经历的时间，t1为从出发到借力时刻所经历的时间，tf为飞行总时间，s为转角系数；λ11，λ13，λ14为第一段轨道的协态变量初值；λ21，λ23，λ24为第二段轨道的协态变量初值。

如图1所示，主要讨论从地球出发的太阳帆通过行星借力和太阳借力加速的时间最优转移轨道设计，属于四点边值问题(Four-Point Boundary Value Problem, 4PBVP)，并且动力学模型复杂，用传统方法求解存在难以收敛、对初值敏感或计算速度慢等缺点。针对这一问题，通过混合优化算法来解决，即先采用遗传算法获得大范围的粗略解形成太阳帆整体飞行轨迹，代入到序列二次规划(Sequential Quadratic Programming，SQP)算法中获得高精度解以加强约束[13]。图2是该套算法的流程图。

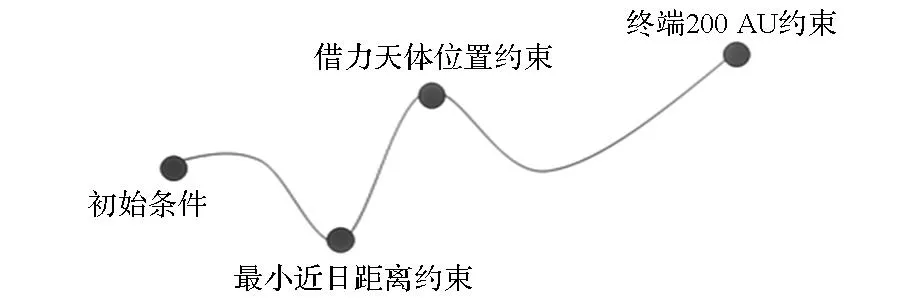
图1复杂约束的四点边值问题Fig.1　4PBVP with complicated path constraints

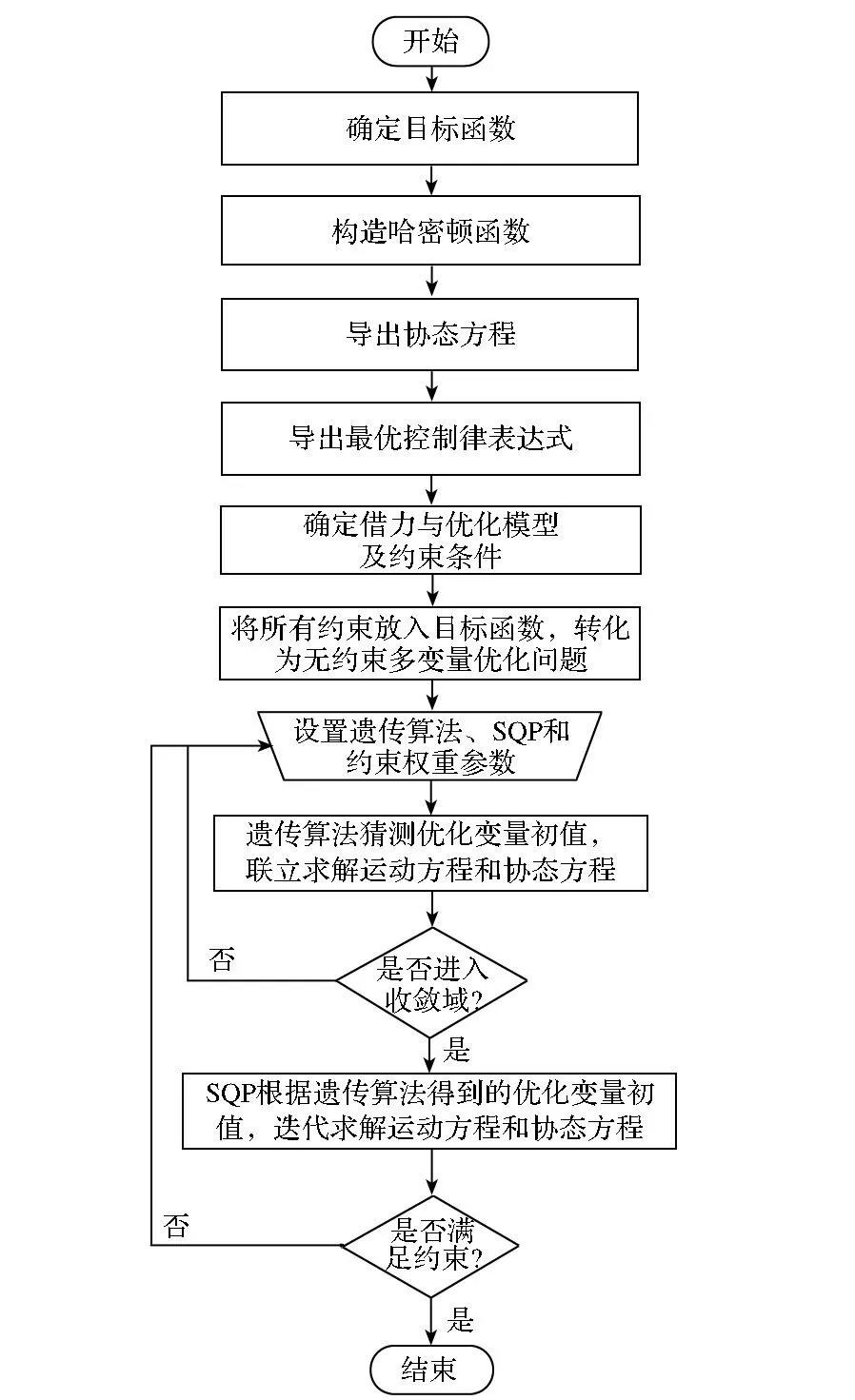
图2　算法流程图Fig.2　Flow chart of algorithm

3算例与分析

为了便于同仅以太阳借力的太阳系逃逸任务轨道对比，仿真参数取自Leipold经典文献的算例[14]。太阳帆的特征加速度ac=0.75 mm/s2，对应的太阳帆尺寸为160 m×160 m，总质量为280 kg。特征加速度小于1 mm/s2，是目前国际上太阳帆能够达到的制造技术水平。2000年左右，NASA提出星际探测器任务[15]，其太阳帆特征加速度选择为3～4 mm/s2，属于高性能太阳帆，远远超过当今的制造技术水平。出发时双曲超越速度C3=0 km2/s2，最小近日距离是0.1 AU，最远飞行200 AU，总飞行时间为21.2 h。图3为该算例的轨道图。

以下借力参数根据实际情况合理选取。太阳帆出发的窗口时间选择在2020年1月1日00:00：00至2035年1月1日00:00：00，借力时间是第100至1000天，整个飞行时间从15年到25年(每年按365.25天算)。选择借力天体为木星，木星的引力常数为1.266 87×108km3/s2，其半径为71 400 km。出发天体为地球，按二体圆轨道进行递推。选择历元为MJD 54000时两个天体的轨道根数，以此时长半轴为圆轨道半径，以此时平近点角为相角，相应轨道参数见表1。

图3　Leipold文献中的最优太阳帆轨迹[14]Fig.3　Leipold’s optimal trajectory with dual solar photonic assist

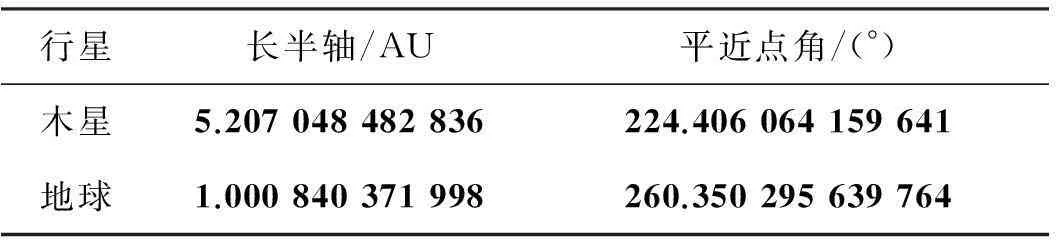
行星长半轴/AU平近点角/(°)木星5.207048482836224.406064159641地球1.000840371998260.350295639764

采用MATLAB的ode113积分器，积分相对和绝对精度为1×10-10。经过反复调试，在算法的最优性和收敛性上做了平衡，遗传算法的参数最终设定为种群代数为10，种群大小为10 000，交叉概率为0.8，精英解保持个数为2；SQP算法最终设定为迭代次数为10 000；目标函数中最小近日不等式约束权重k1=1018，等式约束k2=103，借力天体径向约束权重k3=102，相角约束权重k4=102，借力高度不等式约束k5=1018，终端最远距离约束k6=10，硬约束的权重远远大于软约束。

仿真得到太阳帆出发时刻是2023年12月4日06：37：09，到达时刻是2041年05月10日18：10：58，借力飞行时间是第734.463天，总飞行时间是17.4年。太阳帆距离太阳最近为0.100 004 AU，最远飞行距离距日200.005 022 AU，解来出的初始值是Y=[1 036.981 672 586 412.634 310 670 6109.534 052 051 51.000 000 000 00.842 889 169 70.217 008 775 10.298 441 508 6-0.114 242 867 11.365 045 386 7-0.043 180 891 0]T。

图4　太阳帆飞行至200 AU以远轨道图Fig.4　Sailcraft interstellar trajectory beyond 200 AU

图4为优化得到的太阳帆飞行至200 AU以远轨道，可见算法优化的结果是先进行太阳借力，而后进行行星借力。对比图3和图4，两个轨道在进行太阳借力轨道段是大致相同的，都是进行了两次太阳借力，本文给出的算法算例在太阳帆飞越木星时获得借力，飞行方向发生明显变化，比Leipold算例节省3.8年的时间正是木星借力的结果。

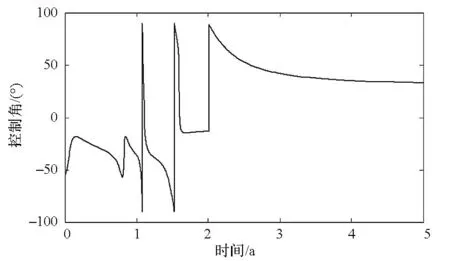
图5　太阳帆控制角曲线图Fig.5　Solar sail control angle curve

图5是太阳帆控制角随时间变化曲线。从图5中可以看出太阳帆姿态角发生3次突变，第1次突变和第2次突变均是太阳帆姿态角从一个极限位置转变到另一个极限位置。结合图6太阳帆速度随时间变化曲线，控制角第1次突变和第2次突变是太阳帆在其远日点进行调整，第3次突变是由木星借力产生。从图6看出，木星借力得到的速度增量将太阳帆加速(Δv=39.920 km/s)，并且使太阳帆速度方向偏转43°。在获得木星加速后，也就是距离太阳5 AU后，太阳帆所受光压力很小，获得加速也很小，抛掉太阳帆更有利于科学载荷开展工作(图5和图6由于后续曲线几乎不发生改变，故只取前5年的变化曲线)。

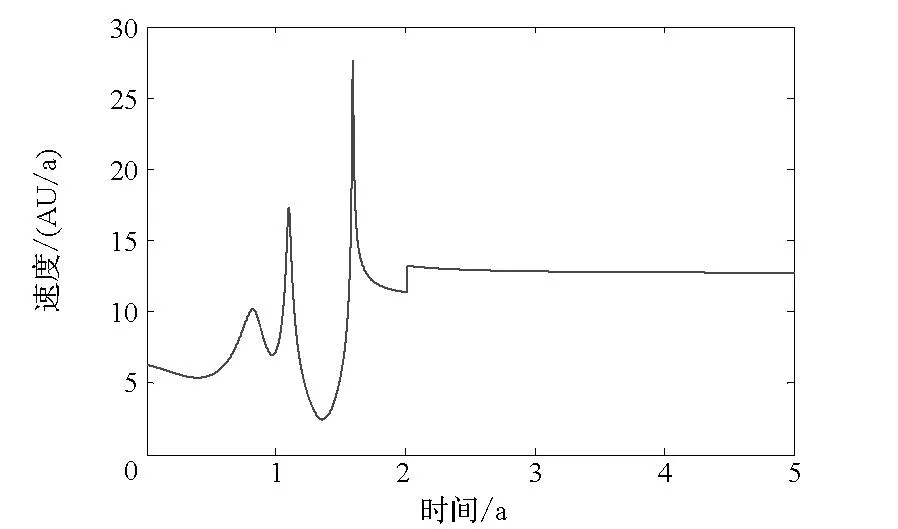
图6　太阳帆速度曲线图Fig.6　Solar sail velocity curve

表2给出了借力时太阳帆与借力天体绝对差，反映太阳帆与借力天体交会时，两者位置差是73 592 km，即借力高度是2192 km；并获得了39.920 km/s的速度增量，相当于8.421 AU/a，使得太阳帆绝对速度增加了1.857 AU/a。

表2　借力时太阳帆与借力天体绝对差

4结论

研究了太阳帆通过行星和太阳借力飞行至太阳系边缘的轨道全局优化问题，将复杂的四点边值问题转换为无约束的参数优化数学模型，通过合理地设计优化目标函数和约束参数，利用混合优化算法，计算得到了满足条件的组合借力逃逸太阳系轨道。仿真结果表明，虽然太阳帆通过太阳借力已获得相当大加速，但加上行星借力仍然可以节省相当多的任务时间；到达木星轨道后，太阳帆所受光压力很小，速度几乎不再发生变化。该太阳帆轨道设计思路，可以为采用行星借力和太阳借力的轨道初步设计提供参考。

参考文献(References)

[1]Quarta A A, Mengali G. Solar sail missions to mercury with venus gravity assist[J]. Acta Astronautica, 2009, 65(3-4): 495-506.

[2]Dachwald B. Optimal solar sail trajectories for missions to the

outer solar system[J]Journal of Guidance Control & Dynamics, 2004, 28(6):1187-1193.

[3]Leipold M. To the sun and pluto with solar sails and micro-sciencecraft[J]. Acta Astronautica, 1999, 45(4-9): 549-555.

[4]Matloff G L, Taylor T, Powell C, et al. Near term interstellar sailing, 20050204038[R]. New York, USA: NYC College of Technology, 2004.

[5]Vulpetti G. 3D high-speed escape heliocentric trajectories by all-metallic-sail low mass sailcraft[J]. Acta Astronautica, 1996, 39(1-4): 161-170.

[6]McInnes C R. Solar sailing: technology, dynamics, and mission applications [M]. London,UK: Springer Verlag, 1999, 112-151.

[7]Kim M. Continuous low-thrust trajectory optimization: techniques and applications [D]. Virginia,USA: Virginia Polytechnic Institute and State University, 2005.

[8]王松霞, 徐世杰, 陈统. 太阳帆飞行器轨道动力学分析[J]. 中国空间科学技术, 2006, 26(2): 30-37.

WANG Songxia, XU Shijie, CHEN Tong. Orbit dynamics analysis of solar spacecraft[J]. Chinese Space Science and Technology, 2006,26(2): 30-37. (in Chinese)

[9]Wie B. Thrust vector control of solar sail spacecraft[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, California,USA, 2005.

[10]钱航, 郑建华. 太阳帆航天器行星际轨道转移优化算法[J]. 空间控制技术与应用, 2012, 38(1): 18-22.

QIAN Hang, ZHENG Jianhua. Optimization algorithm for interplanetary transfer trajectories of solar-sail spacecraft[J]. Aerospace Control and Application, 2012, 38(1): 18-22. (in Chinese)

[11]唐国金, 罗亚中, 雍恩米. 航天器轨迹优化理论、方法及应用[M]. 北京: 科学出版社, 2011.

TANG Guojin, LUO Yazhong, YONG Enmi.Spacecraft trajectory optimization: theory, method and application[M]. Beijing: Science Press, 2011. (in Chinese)

[12]Bryson A E, Ho Y C. Applied optimal control: optimization, estimation, and control[M]. Waltham, Massachusetts,USA: Blaisdell Publishing Company, 1969.

[13]彭祺擘, 李海阳, 李桢, 等.从空间站出发的奔月轨道设计[J]. 国防科技大学学报, 2009, 31(2): 25-30.

PENG Qibo, LI Haiyang, LI Zhen, et al. Trans-lunar trajectory design of lunar probe launched from space station[J]. Journal of National University of Defense Technology, 2009, 31(2):25-30. (in Chinese)

[14]Leipold M, Fichtner H, Heber B, et al. Heliopause explorer-a sailcraft mission to the outer boundaries of solar system[J]. Acta Astronautica, 2006, 59(8-11): 785-796.

[15]Liewer P C, Mewaldt R A, Ayon J A, et al. NASA′s interstellar probe mission[C]//Proceedings of EI-Genk, M.S.Space Technology and Applications International Forum, New York,American Institute of Physics, 2000: 911-916.

Global optimization of solar sail gravity assist and solar photonic assist trajectory for interstellar mission

QIANHang1,3,ZHENGJianhua1,LIMingtao1,LIHui2,GAODong1,YUXizheng1

(1. Key Laboratory of Electronics and Information Technology for Space Systems, Chinese Academy of Sciences, Beijing 100190, China；2. State Key Laboratory of Space Weather, Chinese Academy of Sciences, Beijing 100190, China；3. University of Chinese Academy of Sciences, Beijing 100190, China)

Abstract：With the goal of solar sail mission to near interstellar space (200AU) in 20 years, a global optimization problem of solar sail gravity assist and solar photonic assist trajectory for interstellar mission was studied. A mathematical model for solar sail time-optimal trajectory was established. By taking the constrains of solar sail gravity assist and solar photonic assist into the object function, the four-point boundary value problem of orbit optimization can be converted to multi-variable optimization problem of no constraint. With choosing appropriate constrain proportions, the problem was solved by using genetic algorithm and sequential quadratic programming method. Optimization result shows that plenty of time can be saved by adding Jupiter gravity assist, though solar sail gains a large velocity with solar photonic assist. The proposed global optimization algorithm will provide a reference for the preliminary design of solar system escape orbit.

Key words：interstellar flight; solar sail; gravity assist; solar photonic assist; global optimization of trajectory

中图分类号：V423.6

文献标志码：A

文章编号：1001-2486(2016)01-137-06

作者简介：钱航(1987—)，男，湖北黄冈人，博士研究生，E-mail：qianhang10@mails.ucas.ac.cn；郑建华(通信作者)，女，研究员，博士，博士生导师，E-mail：zhengjianhua@nssc.ac.cn

基金项目：中国科学院战略性先导科技专项资金资助项目(XDA04060303，XDA04076700)

*收稿日期：2015-01-19

doi:10.11887/j.cn.201601022

http://journal.nudt.edu.cn