基于DFT的MIMO雷达发射方向图设计

李奕蓉，胡捍英

(信息工程大学 导航与空天目标工程学院，　郑州 450001)



基于DFT的MIMO雷达发射方向图设计

李奕蓉，胡捍英

(信息工程大学 导航与空天目标工程学院，郑州 450001)

摘要：针对多输入多输出(MIMO)雷达的发射方向图设计问题，为了在保证方向图匹配性能以及空域弱互相关性的前提下，有效降低计算复杂度，提出一种基于离散傅里叶变换(DFT)的方向图设计算法。该算法先依据方向图的匹配性能及空域互相关性构建代价函数，再利用DFT构造发射信号协方差矩阵，从而避免了采用传统凸优化方法引入的极高复杂度。理论分析表明，该算法设计的信号协方差矩阵能够满足方向图设计模型中的基本约束条件，同时使得代价函数最小，具备一定的合理性。仿真及性能分析结果表明，该算法计算复杂度低，且设计出的方向图匹配性能良好、空域互相关性小。

关键词：MIMO雷达；发射方向图；离散傅里叶变换；低复杂度；匹配性能；空域互相关

0引言

多输入多输出(MIMO)雷达是近年来的一种新兴体制雷达[1-3]，按照阵元间距不同，MIMO雷达可以分为分布式MIMO雷达[4-5]和集中式MIMO雷达[6-7]，本文重点对集中式MIMO雷达进行研究。集中式MIMO雷达与传统相控阵雷达结构类似，但不同的是，集中式MIMO雷达可以自由地设计每个阵元的发射信号波形，具备波形分集的能力。通过波形分集可以灵活地设计发射方向图，使电磁波能量有效地聚集到感兴趣的区域内，有利于参数的精确估计以及目标跟踪。因此，研究MIMO雷达的发射方向图设计技术具有重要意义。

MIMO雷达方向图设计主要通过设计发射信号协方差矩阵来逼近期望方向图，再根据信号协方差矩阵设计得到真实的发射信号。本文着重关注信号协方差矩阵的设计方法。文献[8]最早提出了MIMO雷达发射方向图设计的数学模型，并将其转换为半正定二次规划(SQP)问题，利用凸优化工具箱对信号协方差矩阵进行求解。该方法虽然能够较好地逼近期望方向图，但复杂度极高。文献[9]采用梯度搜索法对信号协方差矩阵的Cholesky因子进行优化，同时对代价函数进行改进，一定程度上降低了梯度计算的复杂度，但是整个优化过程仍需多次迭代才能收敛到最优解，复杂度仍然偏高。文献[10]采用切比雪夫加权的基波束合成低旁瓣发射方向图，设计得到的发射方向图具备较低的空域互相关特性，但该方法不能保证每个阵元发射功率相等，降低了雷达的总发射功率，进而降低了探测距离。文献[11]通过傅里叶变换构造能够较好地逼近期望方向图的信号协方差矩阵，计算复杂度较之前算法得到大幅下降，但是，该文献并没有对所设计方向图的空域互相关特性进行考虑。

本文在上述研究的基础上，提出一种基于离散傅里叶变换(DFT)的方向图设计方法。首先，以方向图的匹配性能以及空域互相关性能为依据构建代价函数，利用DFT构造发射信号协方差矩阵，避免了利用凸优化求解信号协方差矩阵带来的极高计算复杂度，从而保证算法的低复杂度特性；然后，对算法的理论依据进行分析，分别从信号协方差矩阵满足方向图设计模型中的约束条件，并且使得代价函数最小两方面验证了本文算法的合理性。

1MIMO雷达信号模型

考虑集中式MIMO雷达系统，发射阵为均匀线阵，阵元数为M，阵元间距为d。发射信号

S=[s(1),s(2), …,s(N)]

(1)

为一窄带信号，N为码长或子脉冲个数，其中

s(n)=[s1(n),s2(n), …,sM(n)]T

(2)

为M×1维矢量，表示在码元时刻n，M个阵元的发射信号；(·)T表示转置运算。为了便于分析，假设电磁波在传播过程中没有衰减，则到达远场方位角为θ处的信号可以记为

x(θ)=aH(θ)s(n)

(3)

其中

为发射导向矢量。

信号x(θ)在N个子脉冲内的平均功率为

aH(θ)Ra(θ)

(4)

式中：R为信号s的采样协方差矩阵；(·)H表示取共轭转置。P(θ)为MIMO雷达的发射信号方向图，反映了一段时间内雷达在空间各处电磁能量的平均分布情况。

定义两个任意方向的互相关方向图为

Pc(θp,θq)=aH(θp)Ra(θq)，θp≠θq

(5)

该式反映了方向图的空域互相关性能，即空间中两个不同方向回波之间的互相干扰程度。

MIMO雷达发射方向图的设计重点在于发射信号协方差矩阵的设计，然后再根据信号协方差矩阵设计实际的发射信号。经典的发射信号协方差矩阵的设计方法[8]是在约束MIMO雷达各阵元功率相同的条件下，利用最小二乘准则对协方差矩阵进行优化，以逼近期望方向图，其数学模型表达如下

(6)

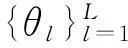
2基于DFT的发射方向图设计算法

在实际中，除了关注所设计方向图与期望方向图的匹配性能外，往往还希望不同角度的回波之间的互相干扰程度尽可能小，以提高后续信号处理能力。因此，本文在设计发射信号协方差矩阵时，对方向图的匹配性能以及空域互相关性能同时进行考虑，对式(6)中的代价函数进行如下改进

(7)

下面首先阐述基于DFT的发射方向图设计算法的具体流程，构造发射信号协方差矩阵的闭式解形式，然后从理论上证明该闭式解能够满足式(6)中的两个基本约束条件，同时还能够使得式(7)中的代价函数最小，以验证所提算法的合理性。

2.1算法描述

设g(n)为一长度为M的序列，则其M点DFT序列可以表示为

(8)

G(k)的离散傅里叶逆变换(IDFT)为

(9)

若G(k)∈{0,1}，则可以利用g(n)构造M×M维Toeplitz矩阵

(10)

式中：(·)*表示取共轭。在总功率约束的条件下，对每个阵元的发射功率进行归一化处理

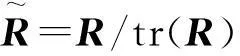
(11)

令

则b(k)与发射导向矢量a(θ)可以通过如下关系式转换

θk=

(12)

设Pd(θ)为期望方向图，其中感兴趣的角度范围为[θminθmax]，则所提的基于DFT的方向图设计算法流程如下。在获得发射信号协方差矩阵后，可根据文献[12]中的循环算法得到真实的发射信号，这里不做赘述。

步骤一：将θmin和θmax代入式(12)得到kmin和kmax；

步骤二：确定G(k)中非零元素的个数及分布范围

{Pi}={k∈Z|M-⎣kmax」+1≤k≤M-⎣kmin」};

步骤三：计算G(k)的M点IDFT序列g(n)；

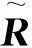
2.2算法合理性分析

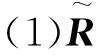
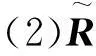
接下来，分别对这两方面进行详细讨论。

2.2.1约束条件证明

命题1若G(k)∈{0,1}，则其离散傅里叶逆变换序列g(n)构成的矩阵R为半正定矩阵。

证明：

由g*(n)=g(M-n)可知，R由[g(0)g(1)…g(M-1)]T及其循环移位序列组成的列向量构成，根据DFT时域循环移位定理可知

n,m=1,2,…,M

(13)

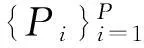
n,m=1,2,…,M

(14)

式(9)中g(n)的表达式可化为

(15)

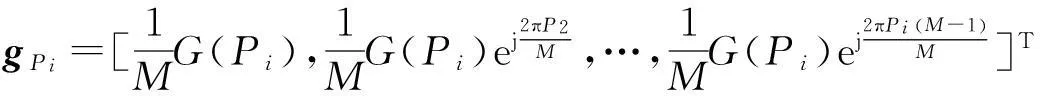
(16)

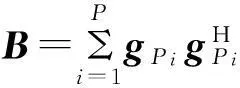
n,m=1,2,…,M

(17)

考虑到G2(Pi)=G(Pi)=1，可以得到B和R的关系式如下

(18)

令h为与R长度匹配的任意列向量，则

(19)

因此，R为半正定矩阵，命题得证。

2.2.2最小化代价函数证明

(1) 方向图匹配性能最优

命题2若G(k)∈{0,1}，且G(M)=G(0)，则bH(k)Rb(k)=MG(M-k)。

证明：

bH(k)R为1×M维向量，其元素为

i=0,1,…,M-1

(20)

则

(21)

命题得证。

由bH(k)Rb(k)=MG(M-k)，可以得到下式成立

(22)

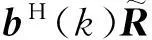
接下来对代价函数J2(R)的第二项，也即方向图空域互相关性最小进行证明。

(2) 方向图空域互相关性最小

参照式(5)中互相关方向图的定义，定义

F(k,q)=bH(k)Rb(q)k≠q

(23)

命题3若k和q均为整数，且当k≠q时，则F(k,q)=0。

证明：

行向量bH(k)R中的元素由式(20)给出，则

(24)

由于离散傅里叶频率k和q均为整数，当k≠q时，0<|k-q|≤M-1，式(24)等于0，即下式成立

F(k,q)=bH(k)Rb(q)=0

(25)

命题得证。

k和q可通过式(12)转换为不同的角度，则式(25)表示空间中不同角度之间的互相关性为0，即保证了式(7)中代价函数的第二项最小。

综上，本文所设计的发射信号协方差矩阵能够满足

(26)

3仿真及性能分析

3.1方向图匹配性能

假设阵元间距为半波长，分别对单波束以及同时多波束情况下，本文算法及文献[8]中的算法(用SQP表示)设计的方向图匹配性能进行仿真。图1中阵元数M=20，期望方向图为空间单波束，感兴趣的角度范围为[-20°20°]。图2中阵元数M=50，期望方向图为空间同时多波束，感兴趣的角度范围分别为[-50°50°]、[-10°10°]以及[30°50°]。由两幅图的结果可知，本文所提算法能够达到与文献[6]一致的方向图匹配性能。

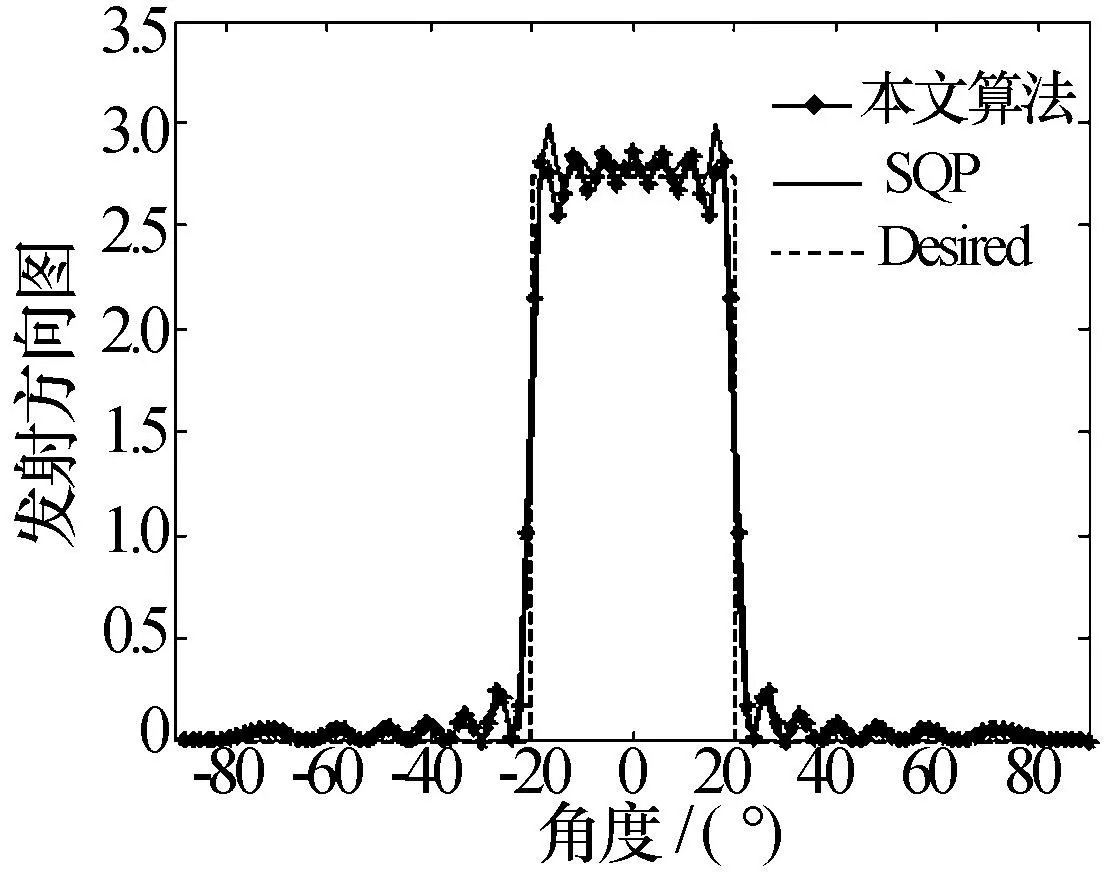
图1　单波束发射方向图

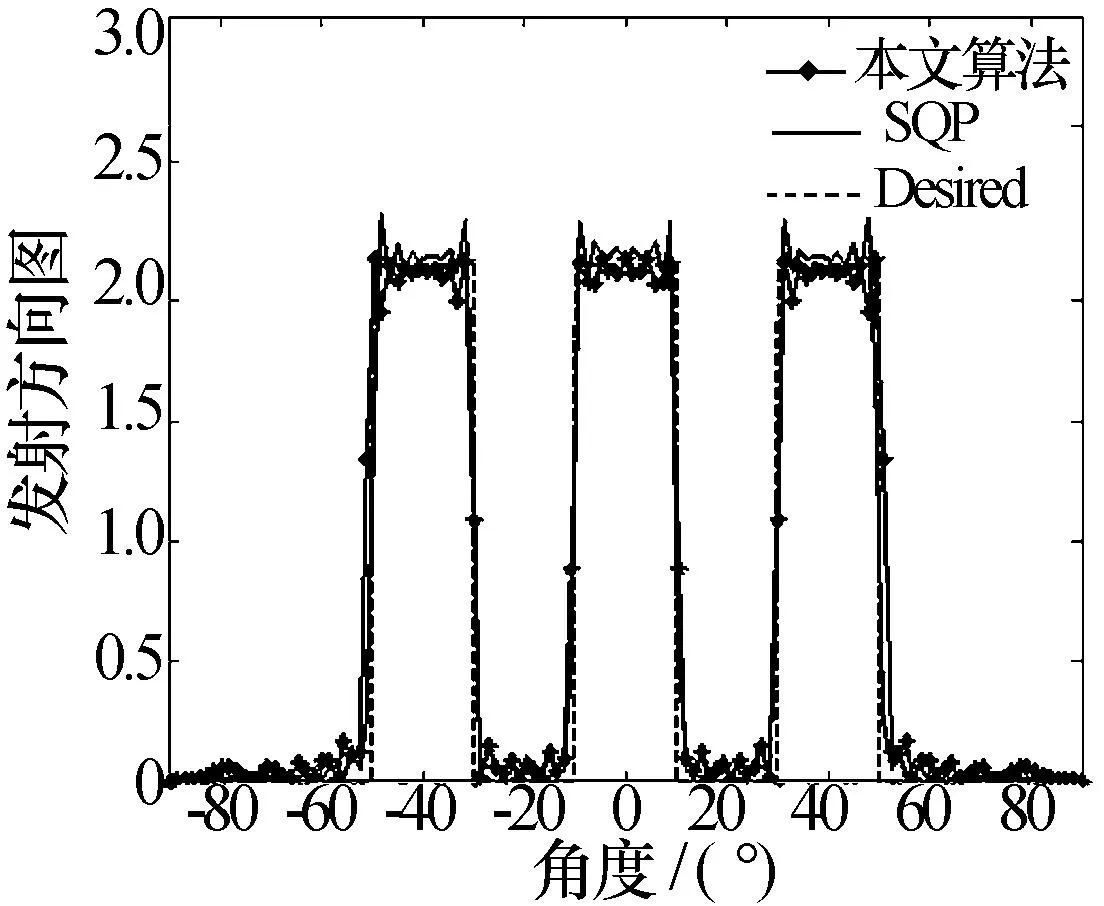
图2　多波束发射方向图

(27)

图3为单波束和多波束情况下，本文算法和SQP所设计的方向图与期望方向图的匹配误差随阵元数的变化曲线。可以看到，随着阵元数的增多，两种算法的匹配误差均减小。在阵元数较少的情况下，多波束的匹配误差要高于单波束，随着阵元数增多，误差逐渐减小，而对于本文算法来说，阵元数对匹配误差的影响更大，尤其是在多波束情况下，为了实现更精确的匹配，需要更多的阵元数。这主要是因为，本文算法设计方向图的性能取决于DFT点数，而DFT的点数与阵元数一致，在多波束情况下，若两个波束靠得太近，则需要更多的DFT点数才能获得更精确的匹配，因此，阵元数量是制约本文算法性能的一个关键因素。但是随着雷达技术的发展，阵元数量的制约得到很大程度的改善，因此本文算法的性能可以得到较好的保证。

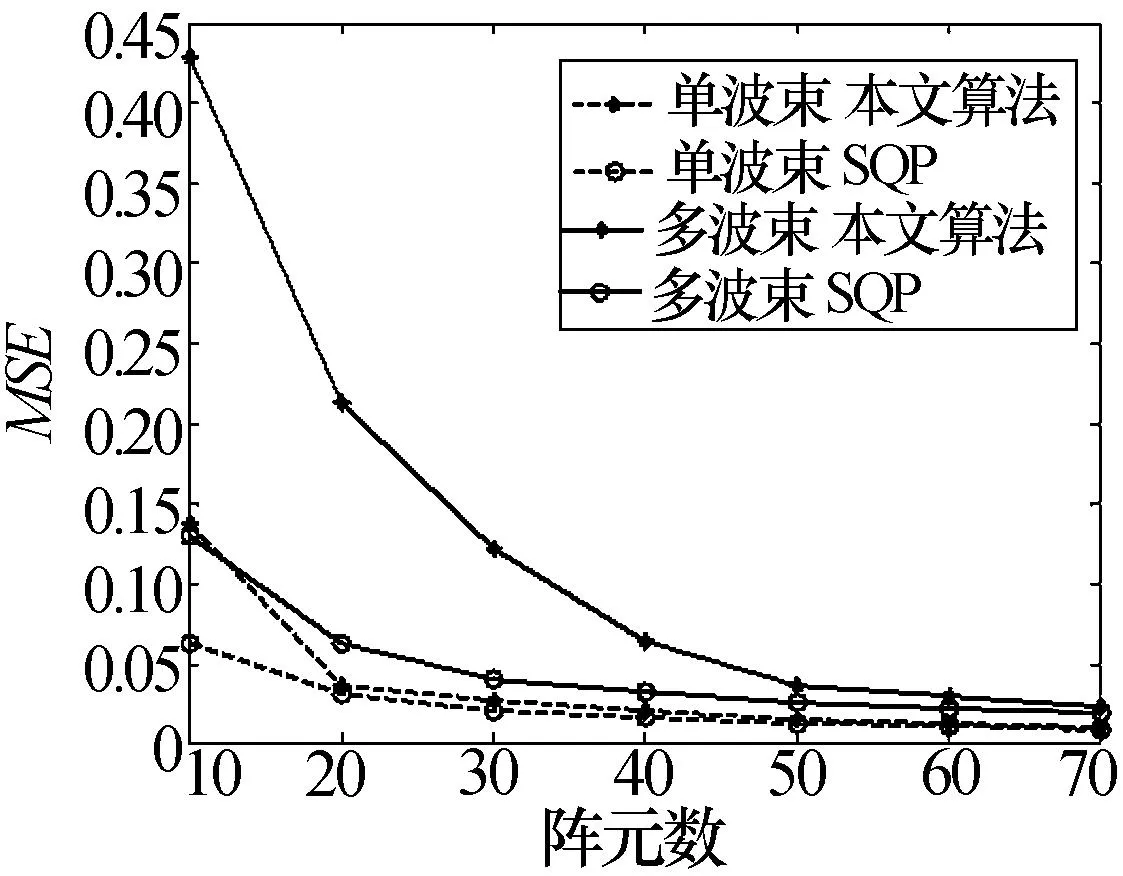
图3　匹配误差随阵元数变化曲线

3.2空域互相关性能

图4为本文算法与SQP所设计方向图的空域互相关性能比较图。本文算法设计的方向图的空域互相关旁瓣明显低于SQP所设计方向图的互相关旁瓣，这主要是因为本文构造的发射信号协方差矩阵能够满足式(24)，理论上，本文设计的方向图的互相关旁瓣应该足够低。但实际上互相关性能没有达到足够低，主要还受到两个因素的影响：(1)角度θ转换为离散傅里叶频率k时，存在取整运算，将会带来计算的误差，影响互相关性能。(2)本文验证的是不同离散频率对应导向矢量之间的互相关为0，转换为角度时，因为阵元数量有限，导致角度间隔不能达到足够小，不能保证空间任意角度之间的互相关性为0。但是，随着阵元数的增多，互相关性能将会得到提升，如图4中c)、d)所示。本文合成的方向图具有较好的空域互相关性能，能够减小不同方向回波之间的互相干扰，提高后续信号处理能力，例如参数估计精度等。

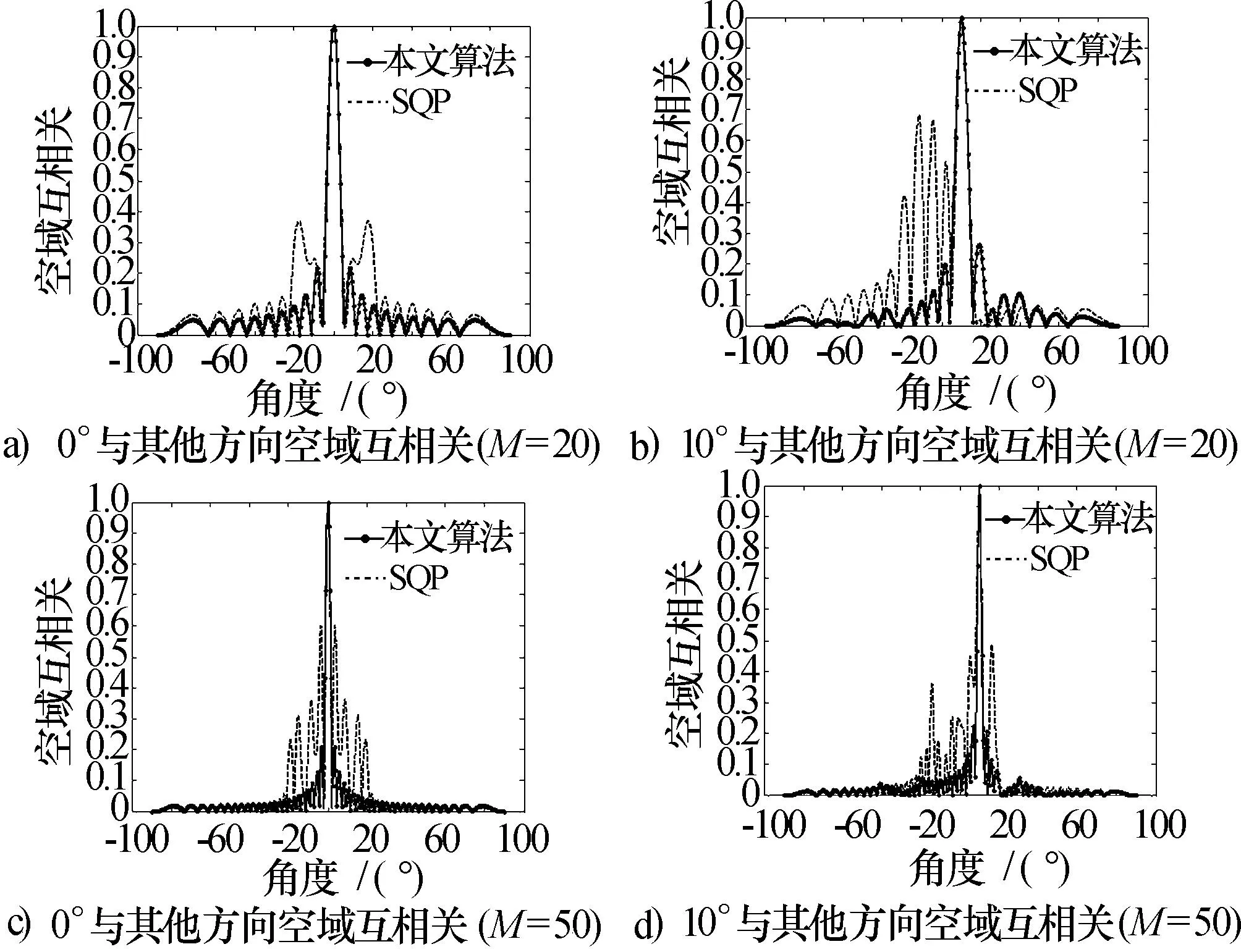
图4　互相关方向图

3.3复杂度分析

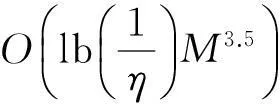
表1　复杂度对比

4结束语

本文提出了一种基于DFT的MIMO雷达发射方向图设计算法。首先，利用DFT构造发射信号的协方差矩阵，保证算法的低复杂度特性；然后，阐述了算法的理论依据，分别从理论上证明了本文构造的协方差矩阵满足方向图设计模型的约束条件，以及利用该协方差矩阵设计得到的方向图具备较好的匹配性能和较低的空域互相关旁瓣。仿真及性能分析结果表明：所提算法具备复杂度低、方向图匹配性能良好以及方向图空域互相关性较小等方面的优点。

参 考 文 献

[1]HASSANIEN A, VOROBYOV S A. Phased-MIMO radar: A tradeoff between phased-array and MIMO radars[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3137-3151.

[2]AHMED S, THOMPSON J S, PETILLOT Y R, et al. Unconstrained synthesis of covariance matrix for MIMO radar transmit beampattern[J]. IEEE Transactions on Signal Processing, 2011,59(8): 3837-3849.

[3]HUA G, ABEYSEKERA S S. MIMO radar transmit beampattern design with ripple and transition band control[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2963-2974.

[4]HAIMOVICH A M, BLUM R S, CIMINI L J. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008,25(1): 116-129.

[5]WANG P, LI H, HIMED B. A parametric moving target detector for distributed MIMO radar in non-homogeneous environment[J]. IEEE Transactions on Signal Processing, 2013, 61(9): 2282-2294.

[6]LI J, STOICA P. MIMO radar with colocated antennas: review of some recent work[J]. IEEE Signal Processing Magazine, 2008,24(5):106-114.

[7]KALOGERIAS D S, PETROPULU A P. Matrix completion in colocated MIMO radar: recoverability, bounds & theoretical guarantees[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 309-321.

[8]STOICA P, LI J, XIE Y. On probing signal design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2007,55(8): 4151-4161.

[9]AITTOMAKI T, KOIVUNEN V. Low-complexity method for transmit beamforming in MIMO radars[C]// Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Honolulu,HI: IEEE Press, 2007: 305-308.

[10]胡亮兵, 刘宏伟, 杨晓超, 等. 集中式 MIMO 雷达发射方向图快速设计方法[J]. 电子与信息学报, 2010, 32(2): 481-484.

HU Liangbing, LIU Hongwei, YANG Xiaochao, et al. Fast transmit beampattern synthesis for MIMO radar with colocated antennas[J]. Journal of Electronics & Information Technology, 2010, 32(2): 481-484.

[11]LIPOR J, AHMED S, ALOUINI M S. Fourier-based transmit beampattern design using MIMO radar[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2226-2235.

[12]STOICA P, LI J, ZHU X. Waveform synthesis for diversity-based transmit beampattern design[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2593-2598.

[13]AHMED S, THOMPSON J, PETILLOT Y T，et al. Finite alphabet constant-envelope waveform design for MIMO radar[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5326-5337.

李奕蓉女，1990年生，硕士。研究方向为MIMO雷达波形设计技术。

Transmit Beampattern Design for MIMO Radar Based on Discrete Fourier Transform

LI Yirong，HU Hanying

(School of Navigation and Space Target Engineering,Information Engineering University,Zhengzhou 450001, China)

Abstract：In order to ensuring good matching performance and low spatial cross-correlation of multiple-input multiple-output(MIMO) radar beampattern, as well as decreasing computational complexity, an algorithm for transmit beampattern design based on discrete Fourier transform(DFT) is proposed in this paper. First, a cost function contains matching performance and spatial cross-correlation is constructed, then a close-form of transmit signal covariance matrix is given by DFT. This method can avoid high complexity caused by convex optimization efficiently. Theoretical analysis indicates that the designed covariance matrix can fully satisfy basic constraints of beampattern design model, meanwhile it can minimize the cost function. Simulation and performance analysis shows that computational complexity of the algorithm is low, and the designed beampattern has good matching performance and low spatial cross-correlation.

Key words：MIMO radar；transmit beampattern；discrete Fourier transform；low complexity；matching performance；spatial cross-correlation

中图分类号：TN957.51

文献标志码：A

文章编号：1004-7859(2016)02-0027-06

收稿日期：2015-10-20

修订日期：2015-12-22

通信作者：李奕蓉Email：liyirong131@163.com

DOI：·信号处理· 10.16592/ j.cnki.1004-7859.2016.02.007