基于探测性能的舰载雷达电磁兼容分析

方小星，朱志宇，张　冰，李　阳2

(江苏科技大学 电子信息学院，　江苏 镇江 212003)



基于探测性能的舰载雷达电磁兼容分析

方小星，朱志宇，张冰，李阳2

(江苏科技大学 电子信息学院，江苏 镇江 212003)

摘要：针对舰船编队时同种雷达较多，相互之间存在电磁兼容影响的问题,利用描述雷达探测性能的最大作用距离的衰减来描述雷达系统中同频段间的电磁兼容程度。首先，分别建立相同工作频段、不同频率雷达间的电磁兼容模型；得到整雷达系统的电磁兼容模型。然后，通过仿真定量分析了模型的雷达间距、压制系数、灵敏度等重要参数对电磁兼容的影响，对发挥协同作战雷达的最大效益提供了数字化分析依据。

关键词：电磁兼容；舰载雷达；最大作用距离；相同工作频段

0引言

舰船编队时，由于同型号军舰的雷达配置上很多都是同种雷达。当同频或者相近频率的雷达同时工作时，就不能忽略雷达间的电磁兼容。电磁兼容性的好坏将直接影响雷达的工作性能，甚至左右一场海战的胜负。所以，需要对雷达间的电磁兼容程度进行预测。国内外研究学者对此作了很多研究，有基于干扰三要素所提出的电磁兼容模型[1-3]，一般都是用辐射源的有效干扰功率与敏感设备的灵敏度门限值的差值得到干扰裕量来预测电磁兼容程度；也有基于雷达的信干比的电磁兼容模型，文献[4]通过分析了雷达检测因子与虚警概率、检测概率的关系，利用综合信干比与检测因子之间的关系来建立电磁兼容模型；文献[5]利用雷达耦合时的干噪比大于检测门限的概率来建立电磁兼容模型。本文利用雷达在受到干扰的情况下，探测能力会降低，其最大作用距离衰减的特性，对整个编队的同频段的舰载雷达建立电磁兼容模型。

1雷达系统电磁兼容模型

1.1相同工作频段非同频时电磁兼容模型

通过雷达方程[6]知道，无干扰时，雷达的最大作用距离为

(1)

式中：P为雷达的发射功率；G为雷达天线增益；λ为雷达发射电磁波波长；σ为目标散射截面积；Smin为雷达最小可检测信号；L为雷达发射并接收电磁波过程中的能量损耗。

L的dB单位表达式为

(2)

式中：L′为大气吸收损耗、雨雪损耗、两部雷达的天线罩损耗、馈线传输损耗等各种损耗的和；LP为极化损耗, 即两部雷达极化方式的差异引入的损耗, 现代雷达大多采用线极化, 如果两部雷达极化方式相同, 极化损失取0 dB, 否则极化损失较大, 一般取20 dB；Lr=(32.5+20lgf+20lgR)为电磁波空间传播损耗, 其中，f为频率(单位为MHz)，R为传播距离(单位为km)。

假设有N部雷达同时工作，且存在同频干扰。一般的情况下，雷达多在同频段非同频状态下工作，此时雷达n收到其他雷达的干扰会受到接收机的选择性曲线产生的对无用发射机发射频谱抑制的影响。此系数(FDR)可由ITU-R SM.337-6建议书得出。

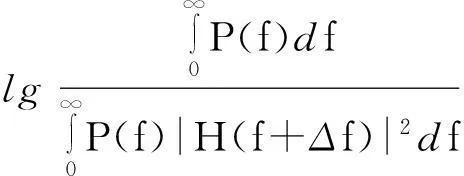
(3)

式中：P(f)为干扰信号等效中频的功率谱密度；H(f)为接收机的频率响应；Δf=ft-fr，ft为干扰源的即时频率，fr为接收机的调谐频率。

FDR可以分为两项，调谐抑制(OTR)和频率失谐抑制(OFR)，后者是由干扰源和接收机失谐产生的额外抑制。

FDR(Δf)=OTR+OFR(Δf)dB

(4)

其中

(5)

第n个雷达收到的其他雷达的干扰Pm可表示为

(6)

式中：Pi为相邻干扰雷达i的发射功率；Gi为相邻干扰雷达i的天线增益；Gn为受干扰雷达n的天线接收增益；γn为雷达i干扰信号对雷达n接收天线的极化系数；Rin为雷达i与受干扰雷达n之间距离；Lin为雷达i发射的电磁波被雷达n接收过程中的能量损耗；FDRni为第i个雷达干扰对雷达n的频率相关抑制系数，这里为一般值，不为dB值；λti为第i个干扰雷达的波长。

雷达n收到的目标信号功率Prs为

(7)

式中：Rn为雷达n与目标的距离；λrn为雷达n的波长。

在受干扰条件下，雷达若要发现目标，收到的目标信号功率Prs和接收的干扰功率Prj(Prj=Prn)必须满足以下条件

(8)

式中：Kn为第n个雷达的压制系数。

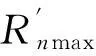
(9)

(10)

1.2可能出现空间对准时电磁兼容模型

1.2.1被干扰雷达可被对准

当被雷达天线对准，接收机前端会出现过载现象，电磁兼容程度很差，可认为电磁兼容程度μ=0。

如果被干扰雷达2和干扰雷达1两个雷达的扫描范围内，就要考虑雷达1对雷达2对准时的情况。假设雷达1、2的距离为R12，以雷达1为球心，R12为半径作一个球面，使得雷达2落在球面上，用雷达1的水平扫描角度ϑ1和俯仰扫描角度θ1将其扫描面积表示出来。同样的方法将对准雷达2的极限面积表示出来，如图1所示。

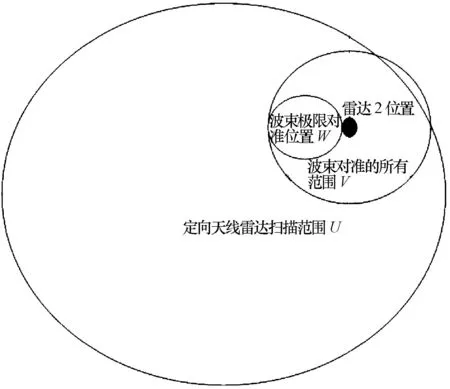
图1　对准范围模拟图

图1中最小的圆是某个时刻的波束的极限对准面积W，将W沿着黑点平移一圈，得到的所有范围为V；U是雷达扫描范围。干扰概率p21为

(11)

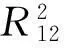
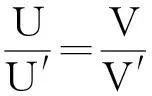
(12)

故p21的最终值与雷达1、2之间的距离无关。

假设有M个雷达对雷达n可对准。雷达i对雷达n的对准概率为

(13)

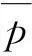
(14)

(15)

1.2.2干扰雷达与被干扰雷达可相互对准

当两个雷达的主瓣波束可以相互对准的时候，既需要避免对其他天线的对准，也需要避免对准其他天线。

首先，由文献[9]知道两个雷达相互对准需要水平方位和俯仰方位都对准，其概率为

(16)

式中：Ph为水平方位对准概率；α1、α2为雷达1和雷达2的天线波束宽度；ϑ1、ϑ2为雷达1、2天线水平扫描区域的角度(ϑ1、ϑ2在文献中默认为360°)；Pv为俯仰方位对准概率；β1、β2雷达1和雷达2俯仰波束宽度；θ1、θ2为雷达1和雷达2俯仰角的扫描范围。

(17)

(18)

那么其电磁兼容程度μ″m为

μ″m=

(19)

1.3舰载相同频段雷达组成的系统间电磁兼容模型

将所有相同频段的雷达组成一个系统，预测整个舰载雷达系统的电磁兼容程度。假设总共有N部雷达，K个雷达可以对准其他雷达，其中有M个雷达可以两两对准，则总电磁兼容程度为

(20)

式中：ηi为第i个雷达的重要系数。

在建立了雷达系统的电磁兼容模型后可以看出，雷达的各种技术参数对电磁兼容程度都有一定的影响。

2算例分析

通过算例分析雷达参数对于电磁兼容程度的影响。为方便计算，将所有雷达放在同一水平面考虑。表1给出了四部同频段(9 000 MHz～9 100 MHz)雷达的主要技术参数。

表1雷达的主要技术参数

假设雷达A～D功率偏移谱密度ΔP(Δf)与接收机的频率响应H(f)为

ΔP(Δf)dB=

(21)

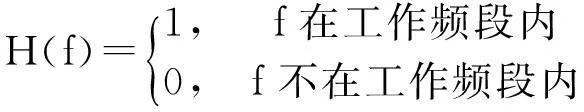
(22)

式中：Δf为与工作频率的偏移。

经计算可得：1/FDRnA≈0.858 2；1/FDRnB≈0.866 8；1/FDRnC≈0.866 8；1/FDRnD≈0.429 3。

2.1雷达间距对电磁兼容程度μ的影响

图2给出了两两雷达之间的电磁兼容性与雷达间距关系图。

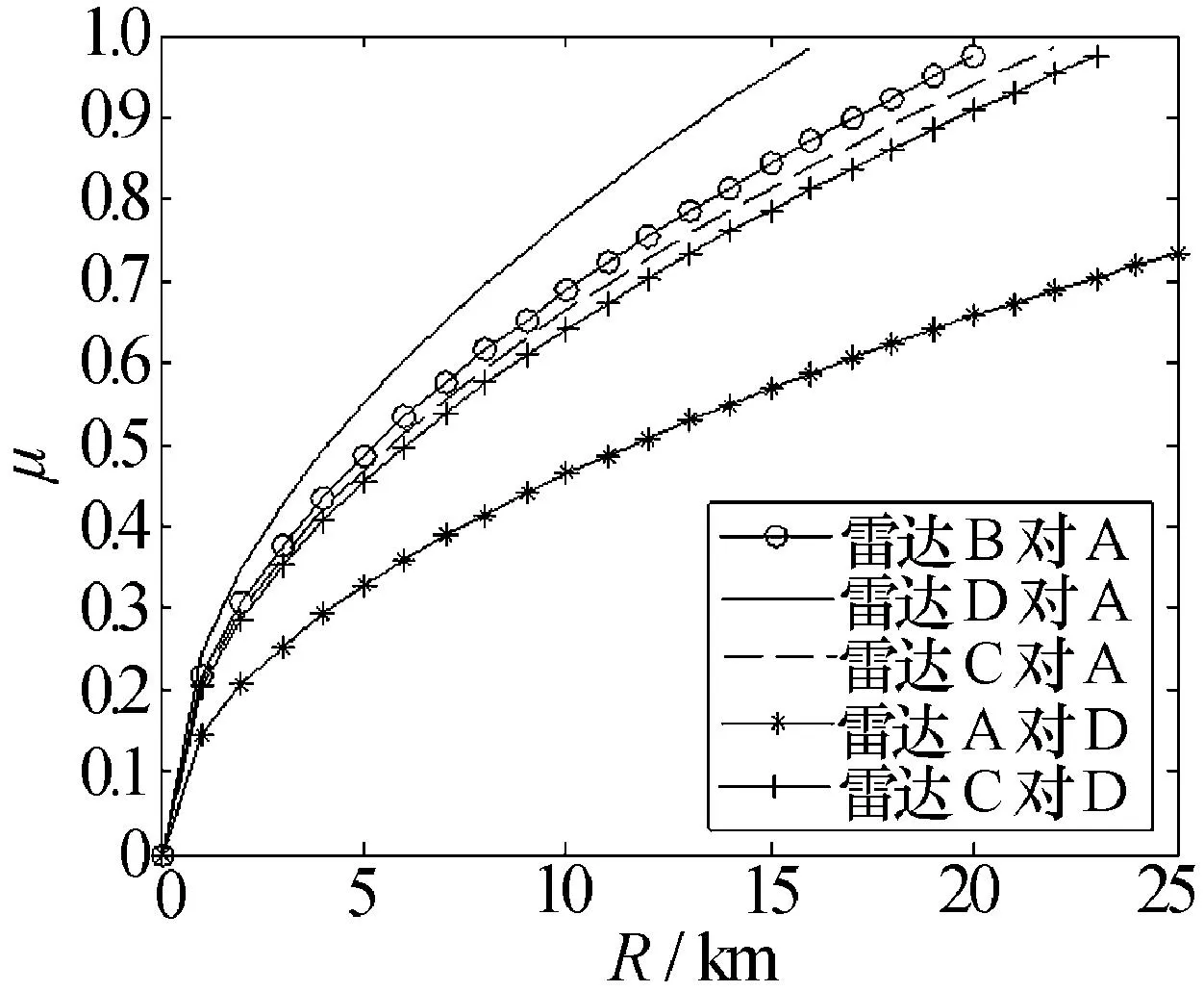
图2　雷达电磁兼容性与雷达间距关系

图2中，μ是电磁兼容程度，R是两雷达相距的距离。由图中雷达B对雷达A曲线、雷达D对雷达A曲线和雷达C对雷达A曲线可以明显看出，雷达C对雷达A的干扰最大，雷达D最小。而且此五部雷达中，雷达A对雷达D的干扰最大，电磁兼容性最差。

2.2雷达重要系数对总电磁兼容的影响

通过雷达间距对电磁兼容程度影响的仿真可以看出两雷达之间距离越远电磁兼容程度越高。现在做如下假设：雷达C与雷达D相距21.2132km、雷达A与雷达C相距22.1044km、雷达D与雷达A相距22.104 4 km；雷达A完全在雷达D的扫描范围内。雷达C、D的重要系数相同，雷达A、C、D三个雷达组成一个雷达协同系统，三个雷达的重要系数总和为1。下面是雷达A重要度系数与整个雷达系统电磁兼容程度的关系。

图3中，η是雷达A的重要系数，Φ是整个雷达系统的电磁兼容程度。从图中可以看出：雷达重要度越大整个雷达系统的Φ越小，说明雷达A对整个雷达系统的干扰程度高。

图3　雷达A重要度系数与总电磁兼容程度关系

2.3雷达灵敏度对总电磁兼容 的影响

假设雷达A、C、D重要度系数分别为0.20、0.35、0.45；分别对雷达A、C、D中的一个雷达灵敏度进行变化仿真时，其他雷达采用表1中的参数。灵敏度越高，最小可检测信号最小。图4是雷达最小可检测信号大小对总电磁兼容的影响图。

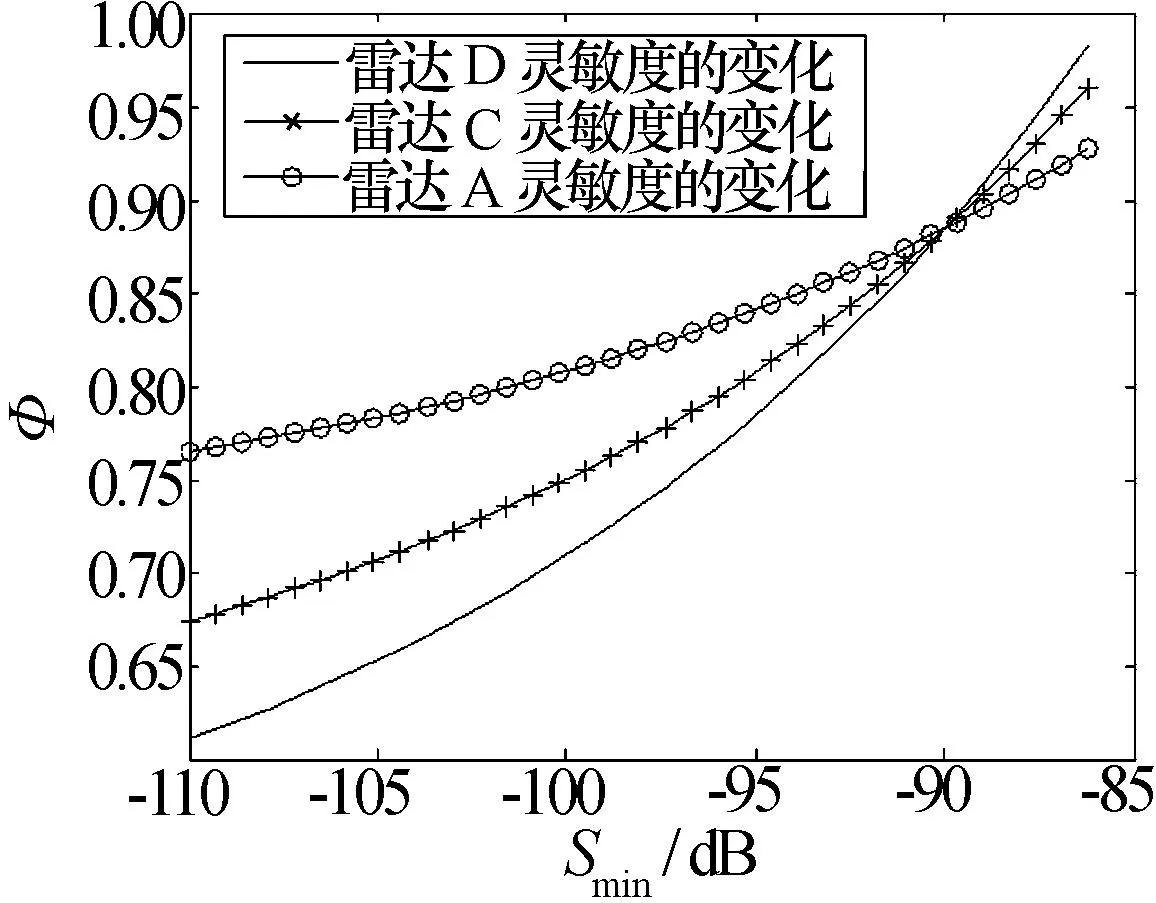
图4　雷达灵敏度与总电磁兼容的关系

图4中Smin是雷达的最小可检测信号大小；Φ是整个雷达系统的电磁兼容程度。从图中可以看出：最小可检测信号越小，灵敏度越高，而整个雷达系统的电磁兼容程度越小，所以雷达灵敏度越高越容易干扰，在雷达A、C、D组成的系统实际工作情况下中，雷达D的灵敏度的增大对Φ影响最大，雷达C次之，雷达A最小。

2.4雷达压制系数对总电磁兼容Φ的影响

下面对雷达的压制系数进行分析，假设雷达A、C、D重要度系数分别为0.20、0.35、0.45；分别对雷达A、C、D中的一个雷达压制系数进行变化仿真时，其他雷达采用表1中的参数。仿真图如图5所示。

图5　雷达压制系数与总电磁兼容的关系

图5中，K是雷达压制系数，Φ是整个雷达系统的电磁兼容程度。图中可以看出：压制系数越大，雷达电磁兼容程度越大，而且雷达A的压制系数的增大对Φ影响最小，雷达C次之，雷达D最大。

3结束语

利用雷达的最大作用距离的损耗大小分析雷达间的电磁兼容程度，建立了整个雷达系统的总电磁兼容程度模型，应用本文提出的分析方法，可以在海战场上进行雷达任务调度时对总电磁兼容程度的影响数字化，对发挥协同作战雷达的最大效益提供分析依据。

参 考 文 献

[1]胡皓全, 杨显清, 赵家升. 雷达之间电磁干扰预测模型研究[J]. 电子科技大学学报, 2001,30(1): 37-40.

HU Haoquan,YANG Xianqing, ZHAO Jiasheng. Research on electromagnetic interference prediction model in radar system[J]. Journal of Electronic Technology University, 2001, 30(1): 37-40.

[2]赵欣楠, 程光伟. 雷达系统间电磁兼容性的计算与预测[J]. 火控雷达技术, 2007, 36(4): 48-51.

ZHAO Xinnan, CHENG Guangwei. Prediction and evaluation of EMC in radar system[J]. Firepower Control Radar Technology, 2007, 36(4): 48-51.

[3]DANIEL W, TAM S, AZU C. A computer-aided design technique for EMC analysis[C]//1995 IEEE Electromagnetic Compatibility Symposium. Atlanta: IEEE Press,1995: 234-235.

[4]王先超, 栗飞. 海战场电子干扰环境下雷达作用距离建模与仿真[J]. 海军航空工程学院学报, 2014, 29(1): 43-46.

WANG Xianchao, LI Fei. Under the sea battlefield electronic interference environment radar distance modeling and simulation[J]. Naval Aviation Engineering College, 2014, 29(1): 43-46.

[5]TERRY F. Antenna coupling model for radar electromagnetic compatibility analysis[J]. IEEE Transactions on EMC,1989, 31(1): 85-87.

[6]马哈夫扎. 雷达系统分析与设计[M]. 刘永坚, 倪嘉骊, 译. 北京：电子工业出版社, 2008.

MAHAFZA. Radar system analysis and design[M]. LIU Yongjian, LI Jiali, translate. Beijing: Publishing House of Electronics Industry, 2008.

[7]李圭源, 张厚, 殷雄, 等. 基于作用距离衰减的雷达间电磁兼容模型[J]. 电讯技术, 2010, 50(3): 49-53.

LI Kuiyuan, ZHANG Hou, YIN Xiong, et al. Radar EMC model based on the role of distance attenuation[J].Telecommunications Technology, 2010,50(3): 49-53.

[8]史豪杰, 邢清华, 刘付显. 基于最大作用距离损耗的雷达间电磁兼容度量新方法[J]. 现代防御技术, 2010, 38(6): 138-140.

SHI Haojie, XING Qinghua, LIU Fuxian. New methods of radar EMC based on the loss of maximum range[J]. Modern Defense Technology, 2010, 38(6): 138-140.

[9]侯民胜. 雷达之间的干扰及概率计算[J]. 雷达与对抗, 2006(2): 16-18.

HOU Minsheng. The interference and probability calculation between the radar[J]. Radar and ECM, 2006 (2): 16-18.

方小星男，1991年生，硕士研究生。研究方向为电磁兼容分析。

朱志宇男，1971年生，教授，硕士生导师。研究方向为电力系统自动化、智能控制、信号与信息处理、电磁兼容等。

张冰女，1967年生，教授，硕士生导师。研究方向为雷达信号处理、电磁兼容。

李阳男，1978年生，博士，讲师。研究方向为电磁兼容。

Electromagnetic Compatibility Analysis of Ship-borne Radar Based on Radar Detection Performance

FANG Xiaoxing，ZHU Zhiyu，ZHANG Bing，LI Yang

(Department of Electronics and Information,Jiangsu University of Science and Technology,Zhenjiang 212003, China)

Abstract：Aimed at the electromagnetic compatibility(EMC) problems between same working band radars on fleet battle ships, radar detection performance such as maximum radar range is used to describe the EMC degree between the radars in radar system. The EMC degree model of entire radar system can be gotten by establishing EMC model of every two radars.Through the simulation, the relationship is analysed between the degree of EMC and several important parameters in the model such as the distance between the radar and so on which provides a digital basis for analyzing maximum benefit of the radar in coordinating combat.

Key words：EMC; ship-borne radar; maximum operating range; same working band

中图分类号：TN959.7

文献标志码：A

文章编号：1004-7859(2016)02-0006-05

收稿日期：2015-10-19

修订日期：2015-12-16

通信作者：方小星Email：fang_xiaoxing@126.com

基金项目：船舶预研支撑技术基金资助项目(13J3.3.5)；江苏省普通高校研究生科研创新计划资助项目(KYLX15_1109)

DOI：·总体工程· 10.16592/ j.cnki.1004-7859.2016.02.002