慢跳跳频信号的时差估计方法

欧阳鑫信，万　群，熊瑾煜，贺　青，文　飞

(1. 电子科技大学 电子工程学院，　成都 611731；

2. 盲信号处理重点实验室，　成都 610041)



慢跳跳频信号的时差估计方法

欧阳鑫信1,2，万群1，熊瑾煜2，贺青2，文飞1

(1. 电子科技大学 电子工程学院，成都 611731；

2. 盲信号处理重点实验室，成都 610041)

摘要：针对慢跳速跳频信号跳带宽、采样率高数据量大的特点，提出了各跳部分数据拼接的跳频信号快速时差估计方法。同时，针对跳频信号的互相关函数存在周期副峰容易导致错误模糊估计的问题，利用先验信息或单跳信号的时差估计值作为引导值，将最终时差估计的搜索范围限定在一个周期以内，避免模糊估计的产生，有效地提高了跳频信号的时差估计精度。仿真结果表明：在信噪比大于8 dB时，提出的跳频信号时差估计方法能精确地估计时差，并且有效抑制周期副峰的影响。

关键词：跳频；时差；周期峰；拼接

0引言

跳频通信具有良好的抗干扰与抗截获性能，在通信领域中得到广泛的应用。目前使用的各种跳频通信系统的工作带宽越来越宽、工作频点越来越多，也向跳频通信的检测与定位提出了严峻的挑战。时差定位是导航与定位的重要手段，而时差定位的关键在于准确地估计时差。时差参数估计是时差定位系统研究的核心内容之一，也是一个研究已久的课题[1-3]，是现代信号处理中信号检测与参数提取问题的一个重要组成部分。时差参数估计研究的基本问题是根据所接收到的目标信号，准确、快速地估计和测定出接收信号相对于基准时间的延迟到达时间(TOA)，或者是不同接收站接收的信号之间由于传播距离不同所导致的相对时间延迟到达时间差(TDOA)，并由此进一步确定其他的有关参量，例如信源目标的距离、方位和速度等。跳频通信信号因其跳变的特点，给时差估计带来很大难题。而对跳频信号进行高精度快速的时差估计有利于对其进行连续实时的定位与跟踪，具有广阔的应用前景。因此，研究跳频信号的高精度快速时差估计算法具有重要的意义。

针对跳频信号的检测、特征参数提取已经有大量的研究工作[4-5]，但针对跳频信号时差估计的研究并不多。文献[6]提出了一种利用跳频信号特征提取参考频率点处的相位差来估计跳频信号的时延，其本质也是利用谱相关拟合相位的方法，这种方法能达到很高的估计精度，但需要先对相位解模糊。文献[7]从跳频信号的特征出发，提出了利用不同跳之间的载波相位差分提取时差的方法，这种方法计算量少，但需要对载波差有较高的估计精度且存在相位模糊的问题需要解决。文献[8]提出一种基于稀疏分解重构的跳频信号时差估计方法，通过重构得到每跳信号的载频和时间中心，从而估计出时差，从其仿真结果来看，其估计精度也有限。文献[9]提出了不同信道条件下接收到的跳频信号模型，并在此基础上提出了跳频信号的最大似然估计算法，在平坦衰落信道下能达到很高的估计精度，但未考虑计算量和周期峰模糊的问题。文献[10]介绍了GSM跳频信号互相关函数的周期峰现象，但未分析此现象的原因以及解决的方法。

本文针对慢跳速跳频信号跳带宽、数据量大的特点，在跳频信号最大似然时差估计算法的基础上，将各跳的部分数据拼接，并利用慢跳跳频信号单跳的时差估计值或者先验信息作为引导值来抑制周期峰模糊的影响，提出了一种各跳部分数据拼接的跳频信号快速时差估计方法。仿真表明提出的方法能快速精确地估计跳频信号时差，并能有效抑制周期副峰的影响。

1跳频信号时差估计方法

1.1信号模型

根据跳频信号的特点，平坦衰落信道下，两个传感器接收到的跳频信号的信号模型可描述为

(1)

式中：sp(t)和Td分别为第p跳信号和驻留时间；τ为信号源到达两个传感器的相对时延；γ1和γ2为接收端的幅度与相位影响因子；n1(t)、n2(t)为相互独立的零均值高斯白噪声，并且都独立于s(t)。

跳频信号跳带范围大，采样率高，直接计算时差的数据量和计算量都很大。因时差估计精度主要受有效带宽影响，受积累时间长度的影响较小。为降低计算量提高处理速度，并能保证得到有效的时差估计，估计用的数据只截取每跳的前T″d(T″d/Td≪1)数据，同时积累多跳信号保证有效带宽基本覆盖跳带范围。多跳拼接处理的信号模型如下

(2)

两路信号的傅里叶变换可表示为

(3)

1.2跳频信号时差估计

当信号与噪声都为高斯白过程，广义互相关算法为最大似然估计[1-2]。广义互相关的算法如下

(4)

因跳频信号在频域上是稀疏的，互相关函数只需要累积频域上很少的数据。设检测到P跳信号的频率成分分别为Bp=[fp-B/2,fp-B/2]，因此频域加权函数Ψg(f)可设为

则式(4)变为

(5)

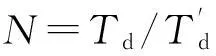
2互相关函数的周期峰

2.1周期峰分析

一个载频为fc、带宽为B、功率为σ2的带限高斯噪声信号，其自相关函数为[11]

Rxx(τ)=σ2sinc(Bτ)ej2πfcτ

(6)

跳频信号可认为是由多个带限信号时域相连拼接组成的，假设信号也为高斯的，则跳频信号的自相关函数为

(7)

式中：M为跳数；B为带宽；σ2为每跳功率；fc为各跳最小载频；Δf为信道间隔；K为跳频信道数。则两路含时差Δt的互相关函数为

(8)

|Rxy(τ)|=σ2βsinc(Bτ)

(9)

(10)

观察上式可以看出，当τ-Δt为1/Δf的整数倍时，β都能取到最大值，即当τ=Δt+n/Δf，n=±1,±2,…时，互相关函数|Rxy(τ)|会产生周期副峰。此时|Rxy(τ)|只受sinc(Bτ)的影响，若周期副峰在sinc函数的主瓣内，则周期副峰容易受噪声影响超过主峰的幅度，导致错误的模糊估计

图1表示无噪声跳频信号互相关函数的归一化结果和sinc函数的主瓣比较情况，图2表示信噪比为5 dB情况下两路跳频信号100次仿真估计的结果。从图1和图2可以看出，跳频函数的周期相关峰的归一化幅度只受sinc函数的影响，主峰两边的副峰在信噪比不高的情况下很容易受噪声影响超过主峰产生错误的模糊估计。

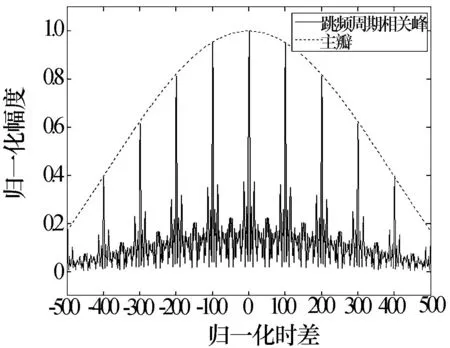
图1　sinc函数主瓣内的跳频周期相关峰

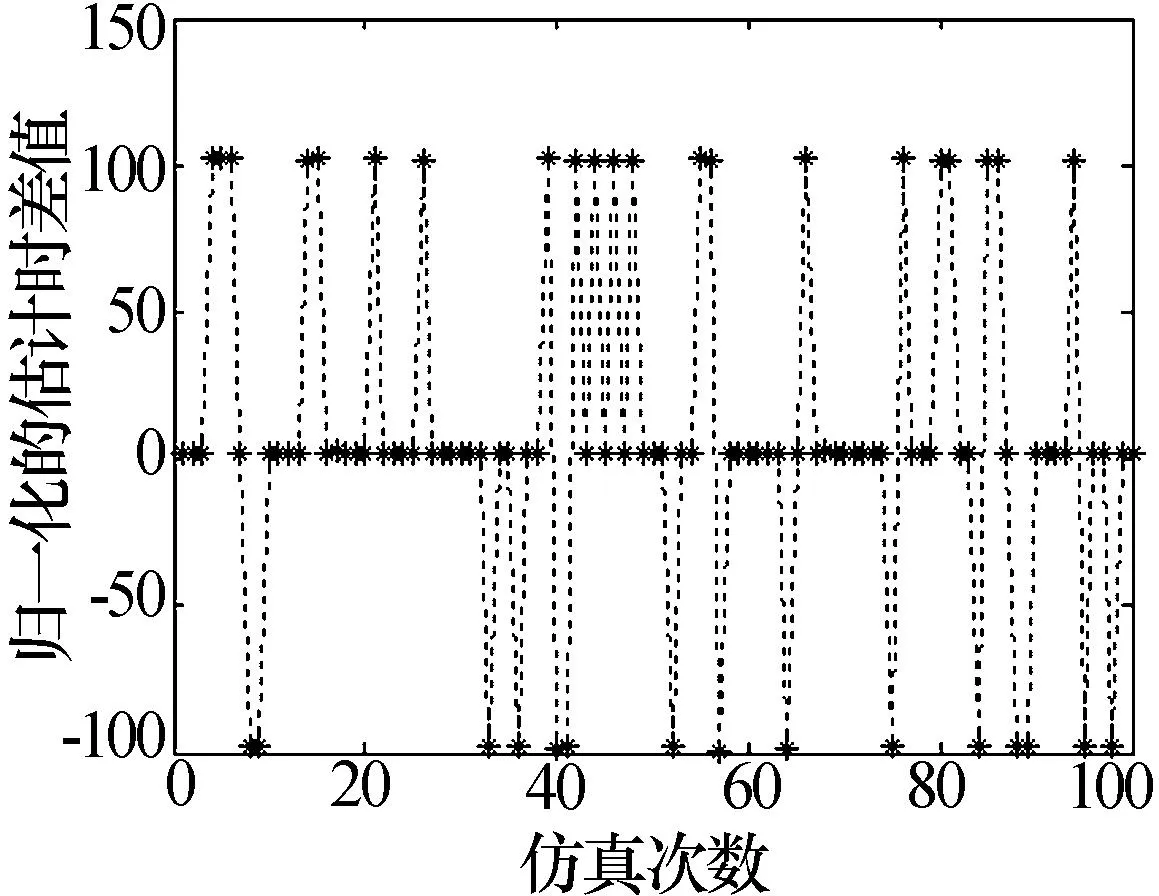
图2　周期副峰引起的模糊估计情况

2.2周期峰影响的抑制方法

可以看出，周期副峰具有一定的周期，如果能把时差搜索范围确定在一个周期内，就不会产生错误的模糊估计。确定时差搜索范围有两种方法：一是根据先验信息如布站情况和辐射源大致位置范围确定时差搜索范围；二是利用慢速跳频信号单跳的时差估计结果作为跳频信号时差估计初始值，在这个初始值的一个周期范围内搜索。第二种方法有效是因为慢跳跳频信号的单跳持续时间比较长，单跳的时差估计精度比较高，单跳的估计结果也具有指导意义。当单跳时差估计精度在一个周期内时，则可以完全消除周期峰的影响。

根据跳频信号参数分析出相关峰的周期后，如果有可利用的先验信息，则可以采用上述第一种方法来确定搜索范围；如果没有，则采用第二种方法来限定搜索范围。

3仿真结果与分析

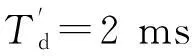
图3表示10跳信号拼接后100次仿真中，有无单跳估计值作为引导值的时差估计模糊出现次数。图4表示四种不同算法100次时差估计的均方根误差情况。其中单跳估计只利用一跳信号的数据，积累时间长度20 ms，每跳取2 ms数据拼接后的10跳信号积累时间长度也是20 ms。

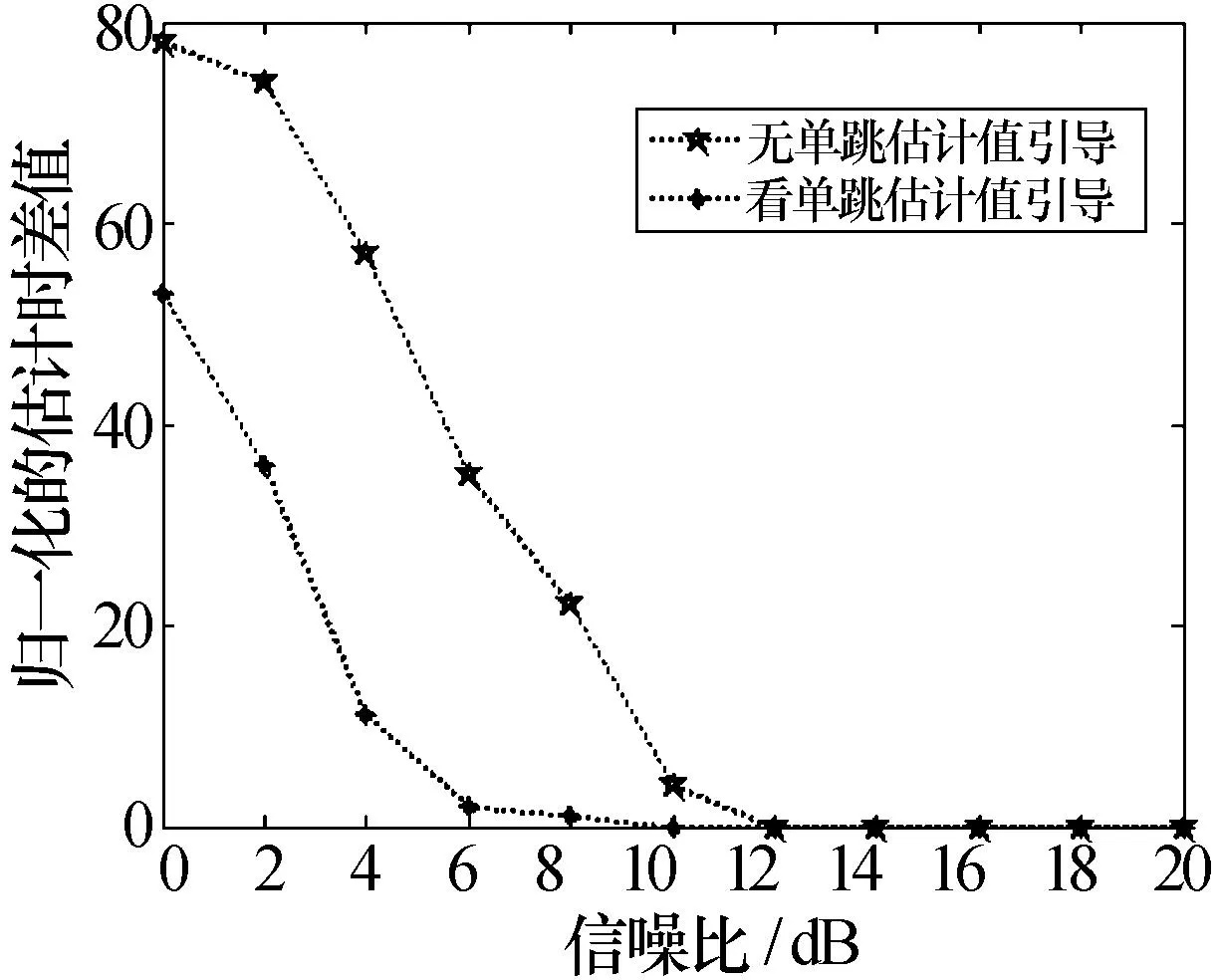
图3　两种算法的模糊估计次数情况

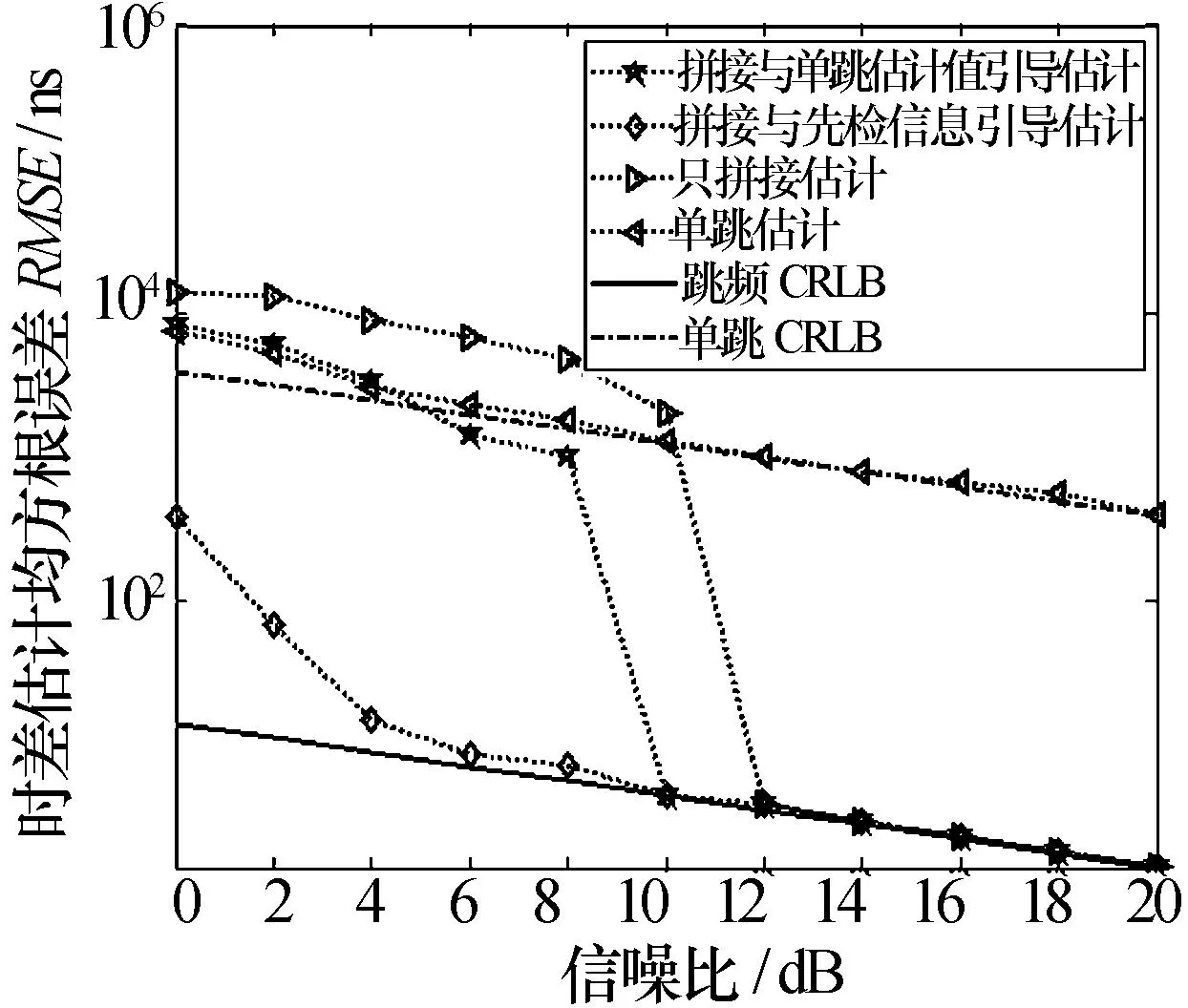
图4　不同算法的时差估计精度对比情况

从图3可以看出，利用单跳数据的估计值作为跳频信号时差估计的时差搜索引导值能降低模糊估计出现的次数，没有单跳估计值引导时，需要12 dB以上才不会出现模糊估计，有单跳估计值引导时，在10 dB以上就不会出现模糊估计的情况了。从图4的算法对比情况图也可以看出，在利用单跳估计值引导的情况下，能有效地抑制模糊估计的影响，在较低的信噪比条件下就能达到很高的时差估计精度，有效提高了时差估计的精度。

分析图4表明：

1)在利用单跳估计值引导的情况下，能有效地抑制模糊估计的影响，在较低的信噪比条件下就能达到很高的时差估计精度，优于无单跳估计值引导的情况；

2)利用先验信息限定时差搜索在一个周期内，能更有效地提高跳频信号的时差估计精度；

3)在出现模糊估计时，无单跳估计值引导的算法要在信噪比高于10 dB时才比单跳估计结果更准确，而有单跳估计值引导的算法在信噪比高于4 dB时就比单跳估计结果更准确；

4)在没有模糊估计时，积累时间、信号速率一样的定频信号与跳频信号的时差估计性能相差悬殊，跳频信号能达到纳秒级的估计精度。

根据图3和图4的仿真结果以及跳频信号时差估计CRLB，可以看出在较低信噪比情况下，跳频信号时差估计精度主要受模糊估计的影响。利用先验信息限定时差搜索范围能很有效地解决这个问题，但应用场景很受限，利用单跳估计值引导虽然达不到非常好的效果，但也能有效地抑制周期峰对跳频信号时差估计的影响。仿真中通过对跳频信号截取再拼接，将处理的数据量和计算量都降低了10倍，有效地提高了系统的处理速度和实时性。

4结束语

本文针对慢跳跳频信号跳带范围大，在时差估计中能够积累的有效带宽大，同时跳带范围大带来采样率高数据量和计算量大的问题，给出了一种慢跳跳频信号多跳截取拼接的时差估计方法，在保证估计精度的同时也大大降低了计算量。拼接的跳数和时间长度可以根据实际情况灵活选择。针对跳频信号相关函数具有周期峰的特性，分别提出了利用先验信息和单跳信号时差估计值来限定时差搜索范围改善周期峰的影响，抑制模糊估计。这种方法也可应用到FSK调制信号等相关函数具有周期峰的时差估计中。

参 考 文 献

[1]KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustic, Speech and Signal Processing, 1976, 24(4): 320-327.

[2]CARTER G C. Coherence and time delay estimation[J]. Proceedings of the IEEE, 1987,75(2): 236-255.

[3]黄桂根, 李品, 丁坚. 宽带干扰信号的数字相关检测与时差估计[J]. 现代雷达, 2015, 37(5): 21-24.

HUANG Guigen, LI Pin, DING Jian. Digital correlation detection and TDOA estimation of broadband jamming signal[J]. Modern Radar, 2015, 37(5): 21-24.

[4]陈新宁. 跳频通信侦察技术研究[D].长沙: 国防科技大学, 2006.

CHEN Xinning. Study on reconnaissance of frequency hopping communication[D]. Changsha: National University of Defense Technology, 2006.

[5]张毅敏. 跳频通信信号参数估计及干扰技术研究[D]. 西安: 西安电子科技大学, 2006.

ZHANG Yimin. Research on the methods of parameters estimate and jamming technology for FHSS communication signal[D]. Xi′an: Xidian University, 2006.

[6]刘伟, 罗景青. 一种新的宽带跳频信号时延估计方法及精度分析[J]. 信号处理, 2010, 26(9):1323-1328.

LIU Wei, LUO Jingqing. A new time delay estimate method of wide-band FH signal and precision analysis[J]. Signal Processing, 2010, 26(9):1323-1328.

[7]WANG J, XU Y, XU P. A linear method for TDOA estimation of frequency-hopping signal[C]// International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM). [S.l.]: IEEE Press, 2012: 1-4.

[8]闫云斌, 全厚德, 崔佩璋. 一种新的跳频信号时延估计方法[J]. 电讯技术，2013, 53(3): 288-292.

YAN Yunbin, QUAN Houde, CUI Peizhang. A novel time delay estimation method of frequency-hopping signals[J]. Telecommunication Engineering, 2013, 53(3):288-292.

[9]徐保根, 万义和, 汤四龙, 等. 不同信道条件下的跳频信号时差估计方法[J]. 四川兵工学报, 2012, 33(11): 86-88.

XU Baogen, WAN Yihe, TANG Silong, et al. TDOA estimation for frequency-hopping signals in fading channels[J]. Journal of Sichuang Weapon Engineering, 2012, 33(11): 86-88.

[10]GOETA A, ROSE R, ZORN S, et al. A wideband crosscorrelation technique for high precision time delay estimation of frequency hopping GSM signals[C]// 41st European Microwave Conference (EuMC).[S.l.]: IEEE Press, 2011: 33-36.

[11]PACE P E, 陈祝明,江朝抒, 等. 低截获概率雷达的检测与分类[M]. 2版. 北京：国防工业出版社, 2012.

PACE P E, CHEN Zhuming, JIANG Chaoshu, et al. Detecting and classifying low probability of intercept radar[M]. 2nd ed. Beijing: National Defense Industry Press, 2012.

欧阳鑫信男，1987年生，博士研究生。研究方向为无源定位、参数估计。

万群男,1971年生，教授,博士生导师。研究方向为阵列信号处理、无源定位。

熊瑾煜男,1975年生,高级工程师,博士生导师。研究方向为无源定位总体技术、超短波信号处理。

贺青男，1984年生，博士，工程师。研究方向为阵列信号处理。

文飞男，1984年生，博士。研究方向为阵列信号处理、参数估计。

TDOA Estimation of Slow-hopping FH Signal

OUYANG Xinxin1,2，WAN Qun1，XIONG Jinyu2，HE Qing2，WEN Fei1

(1. Electronic Engineering College,University of Electronic Science and Technology of China,Chengdu 611731, China)(2. National Key Laboratory of Science and Technology on Blind Signal Processing,Chengdu 610041, China)

Abstract：Since the hop band of slow-hopping frequency hopping (FH) signals is large, the sample rate is very high, and the amount of data needing to be processed is large, a time difference of arrival (TDOA) estimation method based on part data split jointed is proposed for the slow-hopping signals, which can get accurate results quickly. There are periodical peaks in the correlation results of FH signals, and it will bring vague estimation results. To restrain the influence of periodical peaks, two methods are proposed. The first is to set the search range of TDOA in a period with the use of pre-information. The second is to make use of the estimation result of single hop signal, and the TDOA search range will be set in a period include the estimation result of single hop signal. The results of computer simulations demonstrate that the proposed methods can restrain the influence of periodical peaks effectively, and get very accurate estimation results when the signal-to-noise ration is higher than 8 dB.

Key words：frequency-hopping; time difference of arrival; period peak; split joint

中图分类号：TN957.51

文献标志码：A

文章编号：1004-7859(2016)02-0019-04

收稿日期：2015-10-16

修订日期：2015-12-17

通信作者：欧阳鑫信Email：ouyxxwork@163.com

DOI：·信号处理· 10.16592/ j.cnki.1004-7859.2016.02.005