考生作答数据反馈对Angoff标准设定结果的影响

2016-04-07 05:28张咏梅

心理学探新 2016年1期

张咏梅　田　一

(北京教育科学研究院，北京 100191)

张咏梅田一

(北京教育科学研究院，北京 100191)

摘要：以大规模学业成就水平测验为背景，采用组间设计，按类别将专家分为五组，在反馈数据环节随机给予每个专家组未调整的考生真实作答数据和经过上调、下调0.5或1个标准差的调整数据后，采用单因素方差分析与项目反应理论两参数模型考查专家组在标准设定Angoff方法中如何参考使用题目作答数据。结果表明，反馈考生题目作答数据对Angoff标准划定结果有明显影响：反馈未经调整的真实考生题目作答数据影响较大；反馈调整后的高于真实考生题目作答数据影响相对较小，反馈低于真实考生题目作答数据影响相对较大。

关键词：Angoff方法；标准设定；考生题目作答数据反馈

1问题提出

标准设定是标准参照测验编制、实施和结果报告过程中最重要的环节之一，是为测验确立临界分数线(Cut Scores)的过程。标准设定体现了考试目的、内容及测试者能力在广泛的社会或教育环境中的专业价值。依据考试目的，在学业成就水平测试或证书资格考试中，通常需要建立“通过与否”一个或多个临界分数线，如合格线、良好线和优秀线。

Angoff方法作为标准设定领域中应用历史悠久、范围较广的方法之一，由美国学者Angoff(1971)在《教育测量》第二版“评分、常模与等值分数”一章中首次提出。起初，此法要求担当评委角色的专家判断“某等级内最低能力水平的人或人群”能够正确作答每道多项选择题概率或百分率，所有题目概率或百分率总和即为此等级内最低分数或临界分数线。在实施过程中，需要为评委设置数据反馈、小组讨论、多轮评定等环节，增加了这些操作环节后的Angoff方法被称为“调整后Angoff方法”。作为当前国际上采用较多的标准设定形式，调整后Angoff方法在多轮重复评定中，反馈数据通常包括：①常规数据，如某类别考生组在每道题目的完成表现；②影响数据，如在专家评委暂时划定的标准下，预计某参照组可能通过的百分率；③一致性数据，即评委在单个题目上的一致性情况(Hambleton & Pitoniak，2006)。

虽然在标准设定Angoff方法中提供反馈数据已成为重要一环，但在教育测量研究领域就是否反馈数据存在争议。有学者则认为其有利于经验丰富的专家评委将反馈数据与题目内容结合进行整合判断(Clauser，Swanson，& Harik，2002)，也有学者提出专家评委可能会对数据产生过多依赖(Clauser，Harik，Margolis，McManus，Mollon，Chis，& Williams，2009a；Clauser，Mee，Baldwin，Margolis，& Dillon，2009b)，导致忽视题目内容而仅依据数据结果进行判断。

关于数据反馈环节在Angoff法中作用的研究集中于：①反馈数据与判断结果之间是否存在关系？Clauser等(2002)检验了内科医生对于医学证书考试题目所做的判断，发现在未提供考生实际表现数据时的专家判断与以考生实际表现数据为基础的经验性条件概率间仅具有低到中等程度的相关。Clauser等(2009a，2009b)的后继研究检验了在专家判断难度与条件概率间的关系，发现当缺乏真实数据反馈时，两者间相关较低；当提供实际表现数据时，相关显著上升。②如果反馈数据，判断如何改变？Hambleton(2001)提出，提供表现数据对判断的影响“可能更多是在心理方面而非教育测量方面”，并认为这种影响体现在“专家评委估计分数间的变异而非所最终估计的临界分数”；Brandon(2004)对六个为专家评委提供表现数据的研究进行了综述，其中四个研究表明了在临界线上的显著变化。③如何运用反馈数据？Dillon和Walsh(2000)调查了专家评委在判定过程中如何运用反馈数据，研究要求评委挑出那些实际表现数据所体现的情况与评委对考生期待不一致的题目，并报告如何将实际表现数据与以内容为依据的判定相整合？评委们的回答集中在两方面：一是尽管实际表现与预想不同，也应坚持最初以内容为基础的判断；二是实际表现数据反映出之前没有甄别出的题目内容问题，应对判断进行调整。

近十年来，随着标准参照测验在我国教育质量评价、学业成就水平测试、资格证书考试中越来越广泛地应用(常蕤，2008；汪存友，余嘉元，2010)，以Angoff为代表的多种标准设定方法开始在国内引起关注，但就在标准设定过程中反馈数据对所制定分数线影响问题还鲜有涉及。文章采用实验研究的方式，以大规模学业成就水平测试中临界分数线的划定为研究背景，探求Angoff方法中反馈考生作答数据是否会对专家评委分数线制定结果产生影响，专家评委如何运用所提供的反馈数据进行研究，以期为当前标准设定的科学应用提供借鉴。

2研究方法

2.1研究工具和样本

依托北京市2010年五年级语文学科大规模学业成就水平测验进行，在此测验中的学生学业表现是体现区域教育教学质量核心指标。根据需要，将采用标准设定过程制定合格、优秀两条临界学业水平分数线。测验包括55道二级计分题目。有效测试人数为99162人，占本区域五年级学生总人数的94.4%。

2.2研究步骤

2.2.1建立专家评委组

专家评委组共25人(小学语文学科领域课程研究人员5人，教学研究人员10人，一线教师10人)。其中，评委在小学语文学科方面至少具有十年教龄，且一线教师在本年度教授五年级语文课程。

2.2.2实验设计

采用组间设计方式。将三类评委划分为五组，每组5人(1名学科领域课程研究人员、2名教学研究人员和2名一线教师)。在正式评判时，每组评委均需按照一定步骤和要求，对处于“刚刚合格”、“刚刚优秀”水平的学生群体正确作答55道题目的百分率进行逐一判断。

实验过程中，将向五个评委组反馈五种类别考生题目作答数据，即随机向其中一组反馈考生未调整的真实作答通过率，而向另四组随机反馈作调整之后的作答通过率。依据Clauser等(2009b)的研究，作答通过率调整方式为：①将题目真实通过率(答对百分率)转换成自然对数Ln(p/1-p)；②计算所有对数的标准差；③将题目真实通过率的对数进行相应的标准差调整，即分别增加或降低0.5、1个标准差；④将调整后的题目转换回到真实通过率量表上去。因此，反馈的五类题目作答数据组分别为真实作答通过率组T组和调整后作答通过率组T+0.5SE、T-0.5SE、T+1SE、T-1SE组。

2.2.3实验步骤

准备阶段：向评委组介绍五年级语文学业成就测验背景目的及Angoff方法流程，熟悉操作环节。实验阶段：分两轮进行。第一轮呈现55道题目评定表，要求评委组在认真浏览试卷上每道题目后，阅读相关资料，估计每等级内最低能力水平学生群体答对百分率。第二轮向评委组反馈考生题目作答通过率。提醒如果数据显著不同于自己预期，请专家再仔细地阅读题目，进行深入细致的小组讨论。继续鼓励专家小组讨论存在较大判断差异题目，考虑产生组内差异原因。开始第二轮评定。

2.3研究问题及数据分析方法

2.3.1研究问题

研究问题包括反馈考生作答数据是否会对评委组的制定结果产生影响？向各评委组反馈未调整作答数据和调整作答数据后，其更改判断的程度是否相同？同时假设如果评委认为在反馈数据帮助下，能够更清楚地甄别出题目存在的问题从而更改初始判断，那么推断评委会更改那些具有真实作答数据反馈的题目，而对那些具有调整后作答数据反馈的题目或不做调整或做较小幅度调整。

2.3.2数据分析方法

单因素方差分析：在整卷水平，对各评委组制定的测验合格、优秀分数线进行差异分析，检验各评委组初始分数线差异情况及反馈考生题目作答数据后最终分数线差异情况。采用软件SPSS18.0完成数据分析。

在每道题目上，评委均需估计(合格、优秀水平)最低能力考生群体正确回答的概率。对与分数线相对应能力水平的考生群体而言，此概率与项目反应理论下的经验条件概率在逻辑上存在密切相关。而这种对应关系被认为是评价判断划定结果合理性的重要基础，也是Angoff方法的重要组成部分(Clauser et al.，2002)。

依据已有研究的应用情况(Clauser et al.，2002；Clauser et al.，2009b)，采用2PLM来估计临界分数相对应能力水平学生通过某题目的经验条件概率，其所期待的指定能力水平的考生正确反应概率(经验条件概率)被表示为：

a：表示题目区分度，b：表示题目难度，θ：表示能力水平，P：表示为经验条件概率，即能力水平为θ的考生通过某题目的经验条件概率，量表因子D为1.7。

以Hambleton等人(1991)相关方法为依据，确定临界分数对应能力水平为θ的考生群体答对某题目的经验条件概率p(θ)的步骤为：①通过两参数模型获得测验期望分数(原始分数量尺)和能力量尺的关系；②将每位专家对每道题目的判断结果加和求平均，得到测验原始临界分数后，根据测验期望分数和能力量尺的关系，找到相对应学生能力值θ。 ③将每个临界分数所对应的学生群体能力值θ代入各题的两参数模型，即可得到该群体答对每题的经验条件概率p(θ)。

采用软件PARSCALE4.1完成数据分析，且55道题目与模型的拟合系数均在0.8~1.2之间，表明模型拟合良好。

2.3.3相关概率指标说明

PI(合格)，PI(优秀)：第一轮未提供考生题目作答数据前，评委组基于领域内容分别对刚刚达到合格、优秀水平学生群体答对某题目的初始直接的概率判断。

安和庄所属乍舌，就是患得患失的鬼算盘也瞪大了眼睛，因为温文尔雅的萧飞羽竟然能够以内力与修为誉为宇内第一的强者抗衡。紫阳道长对天问大师传音：“试招有三分对七分之嫌。”

PR(合格)，PR(优秀)：第二轮提供考生题目作答数据后，评委组根据反馈作答数据对刚刚达到合格、优秀水平学生群体答对某题目直接的概率判断。

CI(合格)，CI(优秀)：第一轮未提供考生题目作答数据前，根据两参数模型，所得到的评委组基于领域内容确定的合格、优秀水平分数线对应能力水平的学生答对某题的初始经验条件概率。

CR(合格)，CR(优秀)：第二轮提供考生题目作答数据后，根据两参数模型，所得到的评委组根据反馈作答数据确定的合格、优秀水平分数线对应能力水平的学生答对某题的最终经验条件概率。

3研究结果与分析

3.1作答数据反馈对分数线制定的影响——基于对整卷制定结果的单因素方差分析

表1　作答数据反馈对于分数线制定的影响

注：Ⅰ表示第一轮制定结果；Ⅱ表示第二轮制定结果。

单因素方差分析结果由表1所示：对于第一轮评委组判断的结果分析表明，在仅基于领域内容所制定的初始合格线Ⅰ、优秀线Ⅰ方面，各评委组之间不存在显著性差异F(4，20)=0.59，p>0.05；F(4，20)=0.96，p>0.05。对于第二轮评委组判断的结果分析表明，在反馈考生作答数据后，各评委组所制定的合格线Ⅱ、优秀线Ⅱ存在显著性差异F(4，19)=5.73，p<0.01，η2=0.55；F(4，19)=22.55，p<0.01，η2=0.83，说明各评委组接受的学生作答信息对其合格线、优秀线的判定产生了显著影响。具体而言，在接受学生作答信息后，各专家组均有所提高；在优秀分数线上，T组、T±0.5SE组、T+1SE组均有所提高，而T-1SE组有所降低。对于评委组两轮所制定的合格线差值绝对值|Ⅰ-Ⅱ|、优秀线差值绝对值|Ⅰ-Ⅱ|的结果分析表明，在合格线调整幅度方面存在边缘显著差异F(4，19)=2.63，p=0.07，η2=0.36。合格线调整幅度与反馈作答数据的调整幅度间具有中等程度的负相关(r=-0.28)，这意味着作答数据被调整的幅度越大，评委组对于合格线调整的幅度越小。而在优秀线调整幅度方面则不存在显著性差异F(4，19)=0.50，p>0.05，调整幅度与反馈作答数据的调整幅度无关(r=0.001)。

总的来说，作答数据反馈对合格线和优秀线的制定结果产生显著影响。对合格线的影响体现在：在所有专家组均调高合格线的同时，并未贸然随着反馈作答数据的调整幅度而相应增加调整力度，而是在将数据与领域内容进行结合分析后相应减少调整幅度；对优秀线的影响则体现在：虽然在相应调整幅度方面不存在显著性差异，但是当反馈的作答数据明显低于真实作答数据(T-1SE)时，优秀线随之下降。优秀线下调是否出于评委组保证相应优秀率的考虑，还有待于研究证实。

3.2作答数据反馈对分数线制定的作用——基于题目的项目反应理论两参数模型的分析

表2　基于领域内容的初始概率判断(PI)与相应经验条件概率判断(CI)的相关分析

注：*表示相关系数显著(p<0.05)，**表示相关系数非常显著(p<0.01)，下同。评委组基于领域内容的题目初始直接概率判断(PI)与基于两参数模型的经验条件概率判断(CI)之间的相关表明了基于领域内容的初始分数线划定的逻辑合理性程度。结果如表2和图1所示：在未反馈题目作答数据前，①无论是制定合格线还是制定优秀线，PI与CI之间存在低至中等程度的相关(0.21~0.51)。②制定合格线时PI与CI之间的相关程度大都高于优秀线(0.38>0.32，0.48>0.35，0.51>0.27，0.34>0.21)。

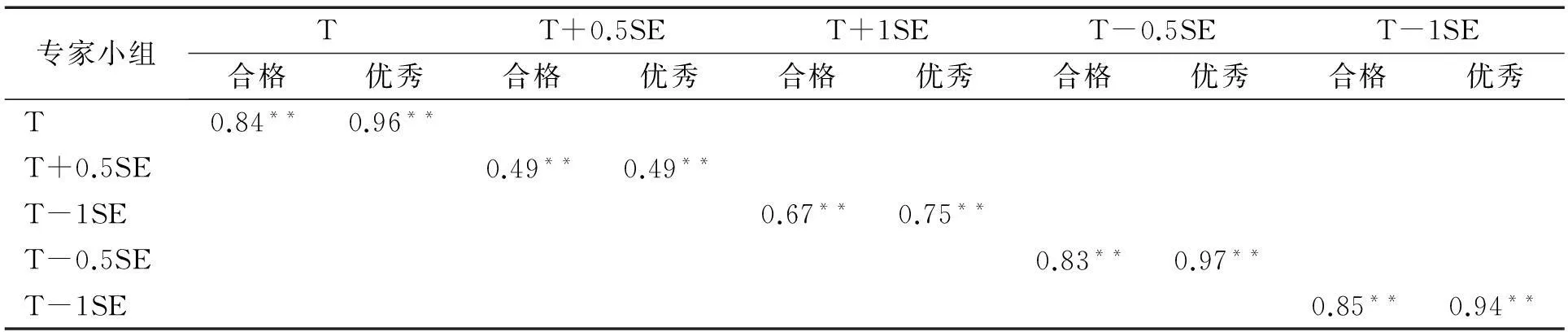
表3　基于作答数据反馈的概率判断(PR)与相应条件概率判断(CR)相关分析

评委组基于反馈作答数据调整后的题目直接概率判断(PR)与基于两参数模型的经验条件概率判断(CR)之间的相关表明了反馈作答数据调整后的分数线划定的逻辑合理性程度。结果如表3和图1所示。在反馈题目作答数据后，①无论是制定合格线还是制定优秀线，PR与CR之间存在中等至较高程度的相关(0.49~0.97)，且较本组表2中PI与CI之间的相关有了较大幅度提高(除T+0.5SE组外)；②对基于真实作答数据反馈的T组而言，PR与CR间的相关已达到很高的程度(0.84，0.96)。虽其与T-0.5SE组和T-1SE组无明显差异，但却明显高于T+0.5SE组和T+1SE组；③在制定优秀线时PR与CR之间的相关程度大都高于合格线(0.96>0.84，0.97>0.83，0.75>0.66，0.94>0.85)。

表2、表3和图1综合反映了在题目水平，反馈和不反馈题目作答数据条件下，评委组的直接概率判断与基于两参数模型的经验条件概率判断之间相关关系的变化情况：①在反馈考生题目作答数据后，专家直接判断概率与基于模型的相应经验条件概率之间的相关均有显著提高，这意味着无论反馈给专家的数据是否属实，前者均受到数据反馈的显著影响。②当反馈的调整后题目作答通过率数据高于真实作答情况时(T+0.5SE、T+1SE组)，评委组受到数据反馈的影响相对较小；而当反馈的调整后题目作答通过率数据低于真实作答情况(T-0.5SE、T-1SE组)，评委组受到数据反馈的影响与T组接近。③制定合格线时PI与CI间相关程度大都高于优秀线，在制定优秀线时PR与CR间相关程度大都高于合格线，可能由于在合格线的制定时相对较大程度地依据所考查的领域内容，而在优秀线制定时则相对较大程度依据所反馈的考生作答数据。

在上述研究结果基础上，深入探求反馈不同条件作答数据即真实作答数据和调整后的作答数据，基于领域内容的初始直接判断对数据反馈调整后判断的影响或者解释程度。与Clauser(2009)研究相同，采用|PI-CI|与|PR-CR|间的相关系数(R)和决定系数(R2)来说明这种影响程度或者解释程度，决定系数越大解释程度越高。

注：RI代表PI和CI的相关系数，RR代表PR和CR的相关系数。图1　基于领域内容概率判断(PI，CI)与基于作答数据反馈概率判断(PR，CR)散点系列图

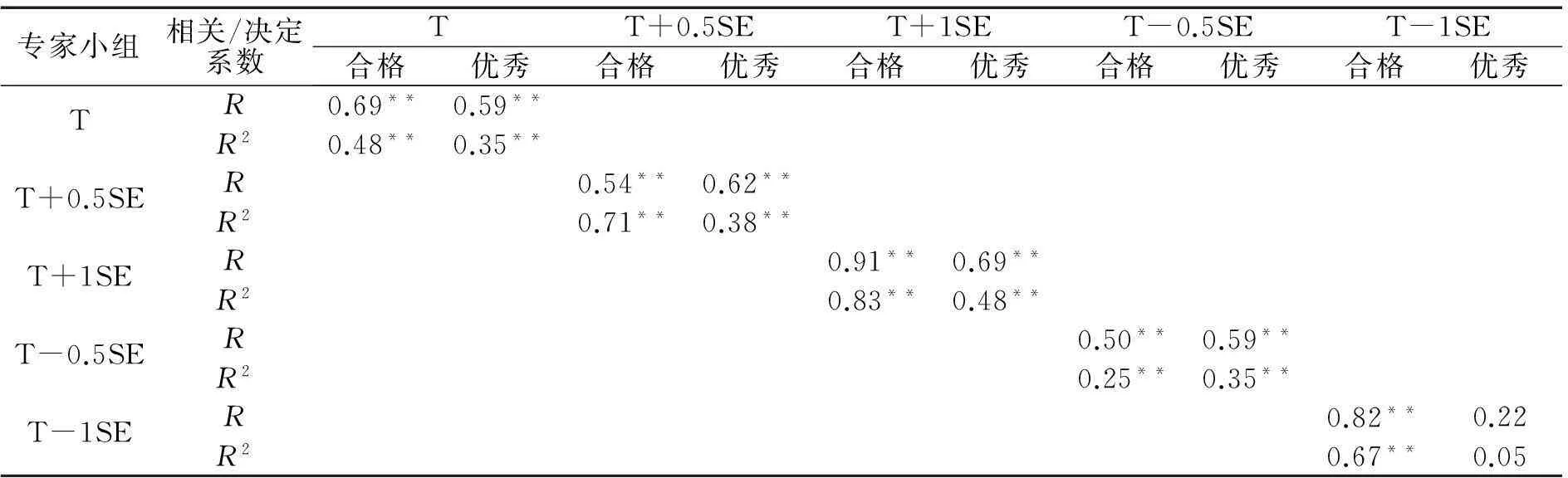
专家小组相关/决定系数TT+0.5SET+1SET-0.5SET-1SE合格优秀合格优秀合格优秀合格优秀合格优秀TR0.69**0.59**R20.48**0.35**T+0.5SER0.54**0.62**R20.71**0.38**T+1SER0.91**0.69**R20.83**0.48**T-0.5SER0.50**0.59**R20.25**0.35**T-1SER0.82**0.22R20.67**0.05

4综合讨论

以大规模学业成就水平测试为背景，通过合格线与优秀线的标准设定过程，考查了评委是否将反馈的考生作答数据结合进Angoff方法且如何运用这些数据的情况，得到两个重要结论：①无论反馈的考生作答数据真实与否，均会对评委制定结果产生明显影响。此与美国学者Clauser等(2002)、Clauser等(2009b)的研究结论相一致。②与反馈真实作答数据组相比，部分被反馈了调整后数据的评委组也对题目做了基于领域内容的相应调整。此结论与Clauser等(2009b)认为所反馈真实数据和调整后数据对评委组产生了“相同程度影响”的结论存在差异。例如，评委组在整卷水平并未依赖作答数据调整幅度而相应增加对合格线的调整力度，在题目水平当反馈的调整后题目作答数据高于真实作答情况时(T+0.5SE组，T+1SE组)，其受到作答数据反馈的影响相对较小。这表明评委在一定条件下，面对调整后数据且没有提供任何关于考生如何作答题目的更深层信息时，依然依赖其领域知识而非仅数据结果，故并未大幅度更改其初始判断。与此同时，还需要关注的是，当反馈的调整后题目作答数据低于真实作答情况时(T-0.5SE组，T-1SE组)，即数据是调整后的且未提供任何关于考生如何作答题目的更深层信息时，专家还是愿意改变其判断。这充分表明评委在一定条件下，还会过重地依赖于反馈数据而非领域知识，且进行了机械地追随和运用。

当前研究还发现与上述结论相关的两个现象：①制定合格线时相对较多地依据了所考查的领域内容，而在制定优秀线时则相对较多地依据了所反馈的考生题目作答数据，推断可能与评委组对学科课程标准的熟悉程度有关。我国当前义务教育阶段的学科课程标准即为合格标准，而优秀标准则未做清晰的说明与界定。因此，评委对于合格水平学生群体所应掌握的内容及程度较为熟悉，而且合格率又是判断教育教学质量的核心基线指标，这或许是对于合格线判断较为慎重且更倚重于领域内容的深层原因。②专家组对低于和高于真实反馈数据值的判断模式不同，高于时更依赖于领域内容。这可能是由于作为学业成就水平测试的标准参照测验，多年来其难度一直较低即考生群体的题目答对率相对较高。因此，在调整后更高的反馈数据可能会引起专家学者的警觉，在基于领域内容找不到充分合理解释的时候，其调整的可能性较小，即使调整其客观可调整幅度也会较小。

图2　基于领域内容的|PI-CI|与基于作答数据反馈的|PR-CR|的散点系列图

综上所述，在应用Angoff方法于标准参照测验分数线制定过程中，是否反馈数据对划定结果的影响极为复杂。在此情况下，简单判定支持或放弃Angoff方法均不可取且也很难保证其他方法就能完全提供基于内容的判断而同时避免实验中所体现的问题。因此，在今后运用Angoff方法制定分数线的过程中，如何有效地设计与实施前期的热身练习并在此过程中引导评委正确解读、运用所反馈的数据信息应为关注重点。此外，由于受客观环境所限，当前实验研究仅选取在真实作答通过率基础上增加或降低0.5、1个标准差的条件下开展，建议在今后同类研究中可设定范围更宽、间隔更细的实验条件进行。

5研究结论

在Angoff标准设定方法中，无论反馈的考生题目作答数据真实与否，均会对合格线和优秀线制定结果产生明显影响；反馈未经调整的真实考生题目作答数据对分数线制定影响较大。与其相比，反馈调整后的高于真实考生题目作答数据对分数线制定影响相对较小，反馈调整后的低于真实考生题目作答数据对分数线制定影响相对较大；反馈考生题目作答数据对合格线制定影响相对较小，即制定合格线较多依赖领域内容的判断；而对优秀线制定影响相对较大，即制定优秀线较多依赖于考生题目作答数据的反馈。

参考文献

常蕤.(2008).一种基于Rasch模型的Angoff方法及其应用.心理学探新，28(4)，76-79.

汪存友，余嘉元.(2010).关于两种Angoff法比较的模拟实验研究.心理科学，33(1)，159-161.

Angoff，W.H.(1971).Scales，norms，and equivalent scores.In R.L.Thorndike(Ed.)，Educationalmeasurement(2nd ed.，pp.508-600).Washington，DC：American Council on Education.

Brandon，P.R.(2004).Conclusions about frequently studied modified Angoff standard setting topics.AppliedMeasurementinEducation，17，59-88.

Clauser，B.E.，Swanson，D.B.，& Harik，P.(2002).A multivariate generalizability analysis of the impact of training and examinee performance information on judgments made in an Angoff-style standard-setting procedure.JournalofEducationalMeasurement，39，269-290.

Clauser，B.E.，Harik，P.，Margolis，M.J.，McManus，I.C.，Mollon，J.，Chis，L.，& Williams，S.(2009a).Empirical evidence for the evaluation of performance standards estimated using the Angoff procedure.AppliedMeasurementinEducation，22，1-21.

Clauser，B.E.，Mee，J.，Baldwin，S.G.，Margolis，M.G.，& Dillon，G.F.(2009b).Judges’ use of examinee performance data in an Angoff standard-setting exercise for a medical licensing examination：An experimental study.JournalofEducationalMeasuremen，46，390-407.

Dillon，G.F.，& Walsh，W.P.(2000).Using performance data to set standards：Practical impact and the perception of judges.CLEARExamReview，11(1)，15-18.

Hambleton，R.K.，Swaminathan，H.，& Rogers，H.J.(1991).Fundamentalsofitemresponsetheory.Newbury Park，CA：Sage.

Hambleton，R.K.，& Pitoniak，M.J.(2006).Setting performance standards.In R.L.Brennan(Ed.)，Educationalmeasurement(4th ed.，pp.433-470).Westport，CT：American Council on Education/Praeger.

Hambleton，R.K.(2001).Setting performance standards on educational assessments and criteria for evaluating the process.In G.Cizek(Ed.)，Standardsetting：Concepts，methodsandperspectives(pp.89-116).Mahwah，NJ：Erlbaum Associates.

Influence of the Feedback of Students’ Performance Data on Standard-setting Result in Angoff Method

Zhang YongmeiTian YiHao YiLi Meijuan

(Beijing Academy of Educational Sciences，Beijing 100191)

Abstract：Based on the large-scale academic test，the study used between group design，divided the experts into five groups，and provided them with the examinee true performance data，up or down 0.5 or 1 standard deviations of the true data.At the same time，the study used one-way ANOVA and two parameter model to test that how the experts read the performance data to set standard in the Angoff method.The results show that the feedback of the data had the significant influence on the setting of the qualified line and the excellent line；the feedback with unadjusted and true performance data had great influence on the standard setting.Compared with that，the feedback with adjusted and above the true performance data had smaller influence on the standard setting，and the feedback with adjusted and below the true performance data had greater influence on the standard setting.

Key words：Angoff method；standard setting；feedback of the students’ performance data

中图分类号：B841.2

文献标识码：A

文章编号：1003-5184(2016)01-0084-08

通讯作者：田一，E-mail：tianyio-001@163.com。郝懿李美娟

心理学探新2016年1期

心理学探新的其它文章: 权力感对为自己和为他人消费行为的影响; 领悟社会支持量表的多元概化分析; CAT中能力参数估计方法的改进：R-MLE估计法*; 微笑影响面孔吸引力判断的眼动研究*; 定量数据分析效应值：意义、计算与解释*; 认知诊断模型下整体和项目拟合指标*