定量数据分析效应值：意义、计算与解释*

蒲显伟

(南京理工大学外国语学院，南京 210094)



定量数据分析效应值：意义、计算与解释*

蒲显伟

(南京理工大学外国语学院，南京 210094)

摘要：由于零假设显著性检验存在的问题，近年来国外许多研究者、期刊编辑和研究学会建议或要求定量研究结果报告效应值作为对显著性检验结果的补充，然而国内心理学、教育学等社会科学领域还很少有学者对效应值进行专门研究。文章将讨论显著性检验存在的问题，效应值的定义及其重要性，效应值的分类、效应值的计算方法和效应值的解释标准。

关键词：效应值；意义；计算；解释

1引言

近几十年来，零假设显著性检验(又被称为零假设检验、显著性检验、统计检验或统计显著性检验，以下简称显著性检验)被广泛地应用于心理学、教育学等社会科学的定量研究中。然而，显著性检验从出现开始，就有学者指出了其存在的问题。Joseph Berkson于1938年在美国统计学会期刊上发表了一篇文章，对显著性检验的内在逻辑和检验效力提出了挑战(Cohen，1994；Kirk，1996)。近年来，研究者对显著性检验的批评更加猛烈(Cohen，1994；Ferguson，2009；Kirk，1996；Schimidt，1996；Sun et al.，2010)。鉴于此，许多研究者建议在定量研究中报告效应值(effect size)作为对显著性检验结果的补充，因为显著性检验只表明研究的统计显著性，而效应值代表研究的实际显著性；同时，国外的一些期刊，也在其编辑方针中明确要求定量研究必须报告效应值；美国心理学会于2010年出版的格式手册第6版(APA 2010，p.33)也明确要求研究者汇报定量研究结果的效应值。受这些建议和要求的影响，国外社会科学领域的一些学者开始在其发表的文章中报告效应值，国内一些心理学期刊，如《心理学探新》，也于2014年开始对效应值的报告作出了明确要求。然而，国内社会科学领域仅有几位学者对效应值的意义和计算方法进行了简单介绍(胡竹菁，2010；胡竹菁，戴海琦，2011；卢谢峰，唐源鸿，曾凡梅，2011；蒲显伟，2014；权朝鲁，2003，等)。因此，本文将对显著性检验存在的问题，效应值的重要性，效应值的分类、效应值的计算方法和效应值的解释标准作一介绍和讨论。

2显著性检验存在的问题

显著性检验是用来判断样本与样本，样本与总体的差异是由抽样误差引起还是本质差别造成的推断统计方法。具体作法是：根据问题的需要对所研究的总体作某种假设，称为零假设，如控制组和接受某种实验处理的试验组没有显著性差异；然后选取合适的统计量，然后根据实测的样本，计算出统计量的值，并根据预先设定的显著性水平进行检验，做出拒绝或接受零假设的判断。通常的判断规则是：当被检验的统计量随机发生的概率等于或小于0.05或0.001时，拒绝零假设；反之就接受零假设。

国外的研究者对显著性检验的批评主要有以下几点。第一、显著性检验的结果与我们所想要知道的研究结果背道而驰(Cohen，1994；Kirk，1996；Larson-Hall，2010)。研究者真正想要知道的是P(H0|D)，即在给定样本的情况下零假设成立的概率。而显著性检验告诉研究者的是P(D|H0)，即在零假设成立的情况下样本发生的概率。第二、显著性检验受样本容量的影响较大(Ellis，2010；Ferguson，2009；Grissom & Kim，2005)。第三、以点为界的二分决策容易让研究者产生误解(Cohen，1994；Kirk，1996；Rosnow & Rosenthal，2003)。统计结果判断的临界点(p=0.05或0.001)是人为设定的，但许多研究者把这一临界点当着判断是非的客观标准，甚至把临界点神圣化了。第四、研究者对显著性检验还有其他方面的错误理解。其中最为普遍的是把统计显著性与实际显著性等同，以及把显著性水平当着是能够成功复制该研究的概率(Cohen，1994；Ferguson，2009；Kirk，1996；Larson-Hall，2010；Volker，2006)。然而，显著性水平只表示在零假设成立的情况下样本发生的概率，效应值才能表明研究结果的实际重要性，检验功效才表示成功复制的概率。

3效应值的重要性

由于显著性检验存在的问题以及人们对显著性检验结果的错误理解和运用，国外好几位学者(如Schmidt，1996)建议禁止使用显著性检验，他们认为显著性检验不仅没有促进，反而严重阻碍了心理科学的发展。然而更多的研究者认为，虽然显著性检验有其内在的缺陷，但大多数问题是由于研究者对其错误的理解和运用而产生的。显著性检验并非完全无用，至少它能证明某一个试验结果是否是由于抽样误差而产生的。因此，这些研究者建议在定量研究结果中增加效应值的报告作为对显著性检验结果的补充(Kirk，1996；Vacha-Haase & Thompson，2004；Volker，2006)。

效应值(又被译为效应量、效果量、效应大小或效应幅度)是指用来量化样本结果与零假设预期偏离程度的统计量(Alhija & Levy，2009；Cohen，1988，1994；Sun et al.，2010)，是独立于测量尺度的统计量，能非常直观地表明组间差异的大小或变量之间关系的强弱，代表的是研究结果的实际显著性，即研究结果在实际生活中的有效性(Ellis，2010)。

效应值的报告不仅是许多研究者的建议，而且是一些学会和期刊编辑方针的要求。早在1994年，美国心理学会出版手册第4版就“鼓励”研究者提供效应值的信息。随着关于显著性检验的争论日趋激烈，美国心理学会又成立了一个推断统计小组(TFSI：the Task Force on Statistical Inference)以研究和解决包括显著性检验在内的关于统计应用的一些有争议的问题(Wilkinson & TFSI，1999)。该小组由各方面的专家组成，包括统计学家、统计学教师、期刊编辑、统计书籍作者、计算机专家和其他特邀的资深专家学者。专门小组的研究结果于1999年在American Psychologist期刊上发表，同时小组建议对出版手册第4版关于统计的章节进行修改。2001年出版手册第5版进一步“建议”研究者在报告显著性检验结果的同时报告效应值。而到了2010年，出版手册第6版则“要求”研究者报告效应值(APA 2010，p.33)。2006年美国教育研究学会(the American Educational Research Association)也发表文章，要求其旗下期刊所刊登的文章必须报告效应值(AREA，2006)。到目前为止，国外社会科学领域共有不同学会的近30种期刊对效应值的报告做出了要求(Sun et al.，2010)。

除了专家学者的建议和要求，效应值在实际运用方面也具有极为重要的作用(Ellis，2010；Grissom & Kim，2005；Larson-Hall，2010；Volker，2006)。首先、效应值能直观地表明组间差异的大小或变量之间关系的强弱，它代表的是研究结果的实际显著性。第二、效应值可以帮助研究者在实验前估计出要使得研究具有统计上的显著性所需要的样本容量。第三、效应值也是功效分析不可或缺的参数。此外、效应值也是元分析者不可或缺的参数。效应值的报告不仅能节省元分析者处理数据的时间，而且能提高元分析的准确性。

4效应值的分类

5效应值的计算

5.1参数检验效应值

表1是常用的参数检验效应值的计算方法(Ellis 2010；Ferguson，2009；Field，2005；Grissom & Kim，2005；Larson-Hall，2010；Levine & Hullett，2002；Volker，2006)。参数检验是在总体分布已知的情况下，对总体分布的参数如均值、方差等进行推断的方法。参数检验的数据必须满足一定的前提条件，如数据呈正态分布、方差齐性、样本独立等(Field，2005；Leech & Onwuegbuzie，2002)。

在t检验中，最为常用的效应值是Cohen’sd，计算方法如表1中公式(1)，即用两组均值差除以两组的平均方差(SDpooled)。其实在Cohen(1988)最初提出的公式中，分母是用总体的方差(σ)而非样本的方差(s)，然而总体的方差难以知晓，因此在实际研究中，一般用样本方差来代替总体方差。当两个组样本容量和方差相似时，可用公式(1)来计算效应值。当两组样本容量相似但方差有较大差异时，用公式(2)，即分母为控制组的方差，因为该组没有接受实验处理，因此其方差更接近总体方差，此效应值被称为Glass’s △。当两组样本容量差异较大时，使用公式(3)来计算效应值，其中分母也是两个组的平均方差。但与公式(1)所不同的是，公式(3)中平均方差是通过对各组的样本方差按样本容量进行加权处理(Ellis，2010，p.10)。

表1　常用参数检验的效应值计算方法

相关分析是研究两个变量之间的相关程度以及相关方向，相关系数为Pearson’sr，也即是分析结果的效应值。统计软件SPSS可以直接输出r值。此外为了便于理解也可以用r2作为效应值。例如，考试焦虑和考试成绩之间的相关系数r为-0.32，那么r2=0.10，该值表示考试焦虑能解释考试成绩10%的变异。平方类的效应值虽然更好理解，但丢失了相关方向(正相关还是负相关)的信息。

回归分析研究一个或多个自变量(其中至少一个是分类变量)与一个因变量之间的关系，尤其是其中一个自变量发生变化对因变量产生的影响。回归分析结果的效应值通常用R2或△R2(adjustedR2)来表示，其含义与r2相同。△R2是对R2所做的校正。统计软件SPSS可以直接输出R2和△R2值。

5.2非参数检验效应值

表2是常用的非参数检验效应值的计算方法(Ellis，2010；Field，2005；Volker，2006)。非参数检验是在总体分布未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。非参数检验方法在推断过程中不涉及有关总体分布的参数，因而被称为“非参数”检验。如前所述，参数检验的一个重要前提条件是数据呈正态分布，虽然参数检验也能容忍数据在一定程度上偏离正态分布，但如果偏离过多，使用参数检验会影响研究结果的准确性。因此，在这种情况下，非参数检验比参数检验更有效力，因为非参数检验对于数据分布和样本大小等没有严格的要求。

在相关分析中，Spearman相关系数(ρorrs)和Kendall tau(τ)相关系数是Pearson相关系数的非参数形式，也是非参数相关分析的效应值。由于数据偏离正态分布，非参数相关分析首先要把原始数据转换为秩(rank)进行检验。当样本容量较小而且转换后的数据有很多相同的秩时一般使用kendall tau系数。

表2　常用非参数检验的效应值计算方法

卡方检验主要是检测列联表中两个分类变量之间的关系，即实际频数与指定分布的频数是否相符。统计软件SPSS输出结果中包含卡方检验统计量χ2及其效应值，如phi (φ)和Cramer’sV(φc)等。另外Cohen’sw也是较常用的效应值。phi (φ) 、Cramer’sV(φc)和Cohen’sw可以分别用表2中公式(6)、(7)和(8)来计算，其中k为列联表中较小的列或联的数值。当列联表为2×N时(N≥2)，那么k值为2，φ、φc和w三个效应值是相等的。需要注意的是，phi (φ)是用来表示2×2列联表的效应值，Cramer’sV(φc)和Cohen’sw可以用来表示任何大小的列联表效应值。此外，更为直观的卡方检验效应值是OR优比值(odds ratio)，其计算方法也比较简单，可参考Field(2005)一书第694页。

Mann-Whitney检验和Wilcoxon符号秩检验分别是独立样本和配对样本t检验对应的非参数检验，其效应值均可用相关系数r来表示。统计软件SPSS不能直接输出r值，但我们可以通过输出结果中的检验统计量Z值用公式(9)来计算，公式中的N为观测个数(observations)。需要注意的是，在Mann-Whitney U检验中，观测个数等于样本大小，而在Wilcoxon符号秩检验中，观测个数等于样本大小乘以2，因为Wilcoxon符号秩检验中同一组受试参加了两次测试。

Kruskal-Wallis检验是一元方差分析对应的非参数检验，其总体效应值为η2，计算方式如公式(10)，即用Kruskal-Wallis检验的统计量χ2除以样本容量减1，SPSS也不能直接输出η2值。与一元方差分析一样，仅知道Kruskal-Wallis检验的总体效应值对于研究者没有太大意义，更重要的是要知道多个独立样本中两两之间的组间差异效应值。然而，Kruskal-Wallis检验并不像一元方差分析一样提供post-hoc多重比较，因此只能用Mann-Whitney U检验对各组进行组间两两比较。

5.3效应值计算软件

在表1和表2中列出的定量研究常用的参数和非参数检验效应值中有一些是统计软件SPSS可以直接输出的，而其他的效应值只能通过SPSS输出结果中包含的描述性数据(如均值、方差等)和检验的统计量(如t值、F值、χ2值等)根据表中所列公式来进行计算。互联网上也可以搜索到很多计算效应值的在线或可下载的软件(表3)。其中功能较强大的是Devilly开发的效应值生成器4.1(Effect Size Generator 4.1)和Wilson的效应值计算器(Effect Size Calculator)。这两款软件都提供不同类型的统计检验效应值的计算，以及不同类型效应值的互相转换。另外效应值生成器4.1还能对保存的检验结果进行元分析。

表3　常用参数和非参数检验效应值计算软件

6效应值的解释

表4是Cohen(1988)提出的解释效应值大小的标准(Ellis，2010，p.41)。以两类效应值最基本的代表d和r为例，当d小于0.2或r小于0.1时，效应值可忽略不计；d大于0.2小于0.5或r大于0.1小于0.3为较小的效应值；d在0.5到0.8之间或r在0.3到0.5之间是中等效应值；而d大于0.8或r大于0.5为较大效应值。

这些标准是Cohen根据多年的研究经验总结出的，一些研究者认为还是比较准确的(Sun et al.，2010)，但也有人对这些标准提出了质疑。Ferguson(2009)在对前人研究进行分析后总结出的社会学领域的解释标准比Cohen的标准要大很多，分别为d=0.41，1.15和2.70。Oswald和 Plonsky(2010)在比较了第二语言习得领域的27个元分析研究后提出的效应值标准分别为d=0.40，0.70和1.00，也比Cohen的标准要大一些。因此，研究者在解释研究结果的效应值时不能机械地照搬这些标准，而应该结合自己研究的领域和研究的目的。更为重要的是，研究者应把自己研究结果的效应值与同领域前人的研究结果的效应值进行对比分析和解释，同时报告效应值的置信区间，提高效应值估计的准确性，这样经过不断的积累和元分析者的努力，各个研究领域就能制定出适合自身特点的效应值解释标准。机械地照搬Cohen提出的效应值解释标准也会使研究者又一次陷入显著性检验以点为界二分决策的错误中。

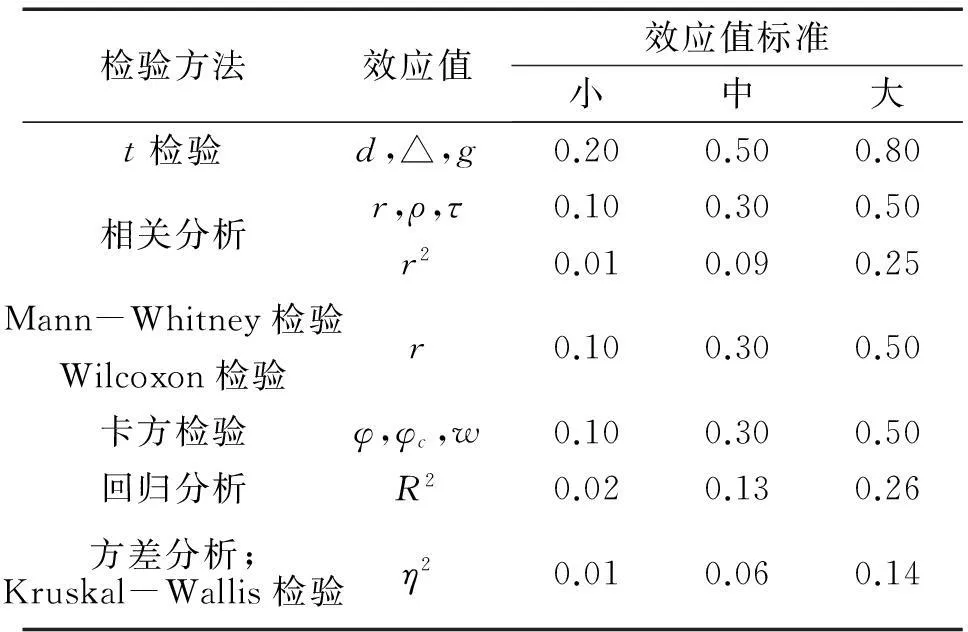
表4　效应值解释标准

7结语

本文介绍了统计显著性检验存在的问题、效应值的定义及其重要性、效应值的分类、效应值的计算方法和效应值的解释标准，以期为国内社会科学领域对效应值不太熟悉的研究者提供一定的参考。在实际研究中，研究者应该根据自己所采用的检验方法选择合适的效应值。本文的另一目的是引起国内社会科学领域定量研究者对效应值的重视。国外的许多研究者、期刊编辑和研究学会都建议或者要求定量研究者在其研究结果中报告效应值，但国内还很少有人进行专门研究。因此，定量研究者不能仅仅满足于汇报研究结果的统计显著性，还应该在此基础上报告研究结果的实际显著性并结合自身的研究领域对其做出更为科学的解释。

参考文献

胡竹菁.(2010).平均数差异显著性检验统计检验力和效果大小的估计原理与方法.心理学探新，30(1)，68-73.

胡竹菁，戴海琦.(2011).方差分析的统计检验力和效果大小的常用方法比较.心理学探新，31(3)，254-259.

卢谢峰，唐源鸿，曾凡梅.(2011).效应量：估计、报告和解释.心理学探新，31(3)，260-264.

蒲显伟.(2014).定量数据分析效应值研究综述.统计与信息论坛，24(11)，18-22.

权朝鲁.(2003).效果量的意义及测定方法.心理学探新，23(2)，39-44.

Alhija，F.N.，& Levy，A.(2009).Effect size reporting practices in published articles.EducationandPsychologicalMeasurement，69(2)，245-265.

American Educational Research Association.(2006).Standards on reporting on empirical social science research in AERA publications.EducationalResearcher，35(6)，33-40.

American Psychological Association.(2010).PublicationmanualoftheAmericanPsychologicalAssociation(6th ed.).Washington，DC：Author.

Cohen，J.(1988).Statisticalpoweranalysisforthebehavioralsciences(2nd ed.).Hillsdale，NJ：Erlbaum.

Cohen，J.(1994).The earth is round (p<0.05).AmericanPsychologist，49(12)，997-1003.

Ellis，P.D.(2010).Theessentialguidetoeffectsizes.Cambridge：Cambridge University Press.

Ferguson，C.(2009).An effect size primer：A guide for clinicians and researchers.ProfessionalPsychology：ResearchandPractice，40(5)，1-7.

Field，A.(2005).DiscoveringstatisticsusingSPSS(2nd ed.).London：Sage Publications.

Grissom，R.，& Kim，J.(2005).Effectsizesforresearch：Abroadpracticalapproach.Mahwah，NY：Lawrence Erlbaum Associates.

Kirk，R.E.(1996).Practical significance：A concept whose time has come.EducationalandPsychologicalMeasurement，56(5)，746-759.

Larson-Hall，J.(2010).AguidetodoingstatisticsinsecondlanguageresearchusingSPSS.New York：Routledge.

Leech，N.L.，& Onwuegbuzie，A.J.(2002).Acallforgreateruseofnonparametricstatistics.Paper presented at the annual meeting of the Mid-South Educational Research Association(Chattanooga，TN，Nov.6-8).

Levine，T.R.，& Hullett，C.R.(2002).Eta squared，partial eta squared，and misreporting of effect size in communication research.HumanCommunicationResearch，28(4)，612-625.

Oswald，F.L.，& Plonsky，L.(2010).Meta-analysis in second language research：Choices and challenges.AnnualReviewofAppliedLinguistics，30(1)，85-110.

Rosenthal，R.，& DiMatteo，M.(2001).Meta analysis：Recent developments in quantitative methods for literature reviews.AnnualReviewofPsychology，52，59-82.

Rosnow，R.，& Rosenthal，R.(2003).Effect sizes for experimenting psychologists.CanadianJournalofExperimentalPsychology，57(3)，221-237.

Schmidt，F.(1996).Statistical significance testing and cumulative knowledge in psychology：Implications for the training of researchers.PsychologicalMethods，1(2)，115-129.

Sun，S.，Pan，W.，& Wang，L.(2010).A comprehensive review of effect size reporting and interpreting practices in academic journals in education and psychology.JournalofEducationalPsychology，102(4)，989-1004.

Vacha-Haase，T.，& Thompson，B.(2004).How to estimate and interpret various effect sizes.JournalofCounselingPsychology，51(4)，473-481.

Volker，M.A.(2006).Reporting effect size estimates in school psychology research.PsychologyintheSchools，43(6)，653-672.

Wilkinson，L.，& APA Task Force on Statistical Inference.(1999).Statistical methods in psychology journals：Guidelines and explanations.AmericanPsychologist，54(8)，594-604.

Effect Sizes in Quantitative Analysis：Significance，Computation and Interpretation

Pu Xianwei

(Nanjing University of Science and Technology，Nanjing 210094)

Abstract：Considering the problems related with null hypothesis significance testing，many foreign researchers，journal editors and research associations have recently encouraged or required the reporting of effect sizes as part of the statistical results in empirical studies.However，few domestic researchers of social sciences have ever studied effect sizes.This article serves as a primer of effect sizes in order to assist researchers of quantitative studies in understanding the significance of effect sizes and in the computation and interpretation of the various types of effect sizes.

Key words：effect sizes；significance；computation；interpretation

中图分类号：B841.2

文献标识码：A

文章编号：1003-5184(2016)01-0064-06

*基金项目：江苏省高校哲学社会科学研究基金项目(2013SJD740018)，中央高校基本科研业务费专项资金项目(NJUSTWGY14001，30920140132029)，南京理工大学教改项目“英语专业创新实验教学体系建设”。