基于光学敏感器增强脉冲星导航系统性能

熊　凯，魏春岭

(北京控制工程研究所 空间智能控制技术重点实验室，北京　100190)



基于光学敏感器增强脉冲星导航系统性能

熊凯，魏春岭

(北京控制工程研究所 空间智能控制技术重点实验室，北京100190)

摘要：本文研究增强X射线脉冲星导航系统性能的方法。脉冲星导航系统以通过X射线探测器测量得到的和通过脉冲星时间模型预测得到的脉冲到达时间之差作为观测量，信号处理过程中，脉冲到达时间差通过观测脉冲轮廓和标准脉冲轮廓的比对来计算。由于构造观测脉冲轮廓需要用到航天器位置信息，脉冲星导航系统的定位性能会受到航天器初始位置误差的影响。为了解决这一问题，提出采用基于“脉冲星+光学”的组合导航方法，将紫外导航敏感器测量信息引入脉冲星导航系统，该方法能够在航天器初始位置误差较大的情况下，显著改善TOA测定精度和导航系统性能。通过数学仿真和对比研究验证了所设计的组合导航方法的有效性。

关键词：自主导航；X射线脉冲星；光学导航；相位估计；航天器

0引言

航天器自主导航系统通过自身设备确定航天器的位置和速度，能够减轻航天任务对地面测控的依赖，提高航天器的自主生存能力。在过去的20 a里，全球定位系统(global positioning system，GPS)是低轨卫星的重要导航手段。但是，由于GPS主要对地面目标提供服务，当航天器在高于GPS卫星的轨道上运行或执行深空探测任务时，GPS信号往往非常微弱，甚至无法接收到有效的GPS信号。此外，还要应对GPS受到干扰或破坏的情况。因此，在利用GPS进行导航的同时，有必要探索新的自主导航方式[1]。

X射线脉冲星能够发射具有稳定周期的脉冲信号，是理想的导航天体源。脉冲到达时间观测量反映了航天器相对于太阳系质心的位置矢量在脉冲星视线矢量上的投影，可用于确定航天器的位置和速度[2-8]。在航天器上通过X射线探测器获取的原始观测量是光子到达时间。通过对光子到达时间观测量的处理获取脉冲到达时间，是脉冲星导航算法的核心环节[9-12]。常用的信号处理方法是通过周期折叠构建观测脉冲轮廓，并将观测脉冲轮廓与标准脉冲轮廓模板进行相位比对，二者之间的相位差反映了脉冲到达时间差，进而将计算得到的脉冲到达时间差观测量用于导航解算。应当说明，为了消除相对论效应和多普勒效应的影响，在应用周期折叠方法获取观测脉冲轮廓之前，需要将光子到达时间转换至太阳系质心。然而，如果航天器的位置和速度是未知的，那么，时间转换和周期折叠无法准确进行，此时，观测脉冲轮廓会变得模糊，从而造成脉冲到达时间差的不确定性。

本文研究通过光学敏感器增强X射线脉冲星导航(X-ray pulsar-based navigation，XNAV)系统性能的方法。针对航天器位置误差影响脉冲到达时间(time of arrival，TOA)之差测定精度的问题，提出引入先进光学敏感器测量信息辅助进行导航，将通过光学导航获得的位置信息用于建立时间转换方程，对原始脉冲星光子到达时间观测量进行时间转换和周期折叠。通过数学仿真考察了航天器初始位置误差对脉冲到达时间差计算精度的影响，分析了初始误差较大的情况下，基于“脉冲星+光学”的组合导航方法对改善脉冲到达时间差测定精度和位置估计精度的作用。

1X射线脉冲星导航

本节介绍脉冲星信号的时间转换和周期折叠等处理方法，指出在计算脉冲到达时间差的过程中，需要用到航天器位置信息，航天器位置误差会对脉冲到达时间差测定产生不利影响。

1.1X射线脉冲信号

脉冲星导航系统的原始观测量是通过航天器上的X射线探测器获得的光子到达时间。光子到达时间通常建模为泊松过程，并通过周期性的脉冲轮廓函数λ(t)≥0来描述，在非重叠时间窗口内的光子数为独立的泊松随机变量。在时间窗口(s，t)内到达光子数为Ns，t的概率为

(1)

式(1)中，Ns，t为在时间窗口(s，t)内到达的光子数，泊松过程的积分速率为

(2)

光子数Ns，t的均值和方差分别为

E(Ns,t)=var(Ns,t)=Λ(s,t)

(3)

脉冲轮廓函数反映了来源于所观测的脉冲星和宇宙背景中的所有光子到达X射线探测器的平均速率，该函数如(4)式所示。

λ(t)=λb+λsg(t)

(4)

式(4)中，λb和λs为已知常数，分别表示来源于宇宙背景和作为导航信号源的脉冲星的光子到达速率。函数g(t)用于描述脉冲星光子到达速率的周期性变化。函数g(t)是非负的，满足式(5)及式(6)

(5)

mint∈[0,Tp]g(t)=0

(6)

函数g(t)定义在时间区间t∈[0,Tp]内，在式(5)和式(6)中，Tp表示脉冲周期。该定义可周期延拓到整个时间轴，即

g(t+nTp)=g(t)

(7)

式(7)中，n是正整数。脉冲星各个周期的光子流量变化情况可以用一个周期的脉冲轮廓函数来描述。

1.2时间转换

在脉冲星导航系统中，用于修正航天器位置误差的是脉冲到达时间差，即通过X射线探测器测量得到的和通过模型预测得到的同一脉冲到达指定空间参考点的时间之差。脉冲到达时间差可通过观测脉冲轮廓与标准脉冲轮廓相位比对的方式来计算。通常选择太阳系质心(solar system barycenter，SSB)作为进行相位比对的空间参考点，原因在于SSB相对于脉冲星的加速度很小，在SSB可以观测得到稳定的、周期性的X射线脉冲辐射，脉冲辐射随时间变化的情况可以简单的用类似周期函数的形式来表述。脉冲到达时间差反映了航天器位置误差在脉冲星视线矢量上的投影，基本概念如图1所示。

为了在SSB构建观测脉冲轮廓，在航天器上观测到的光子到达时间需要转换到SSB。在时间转换过程中，除航天器位置变化对光子到达时间的影响之外，还需要考虑航天器运动对时钟的影响，以及太阳系重力场效应等因素。光子到达航天器的时间和到达SSB的时间之间的关系可用如(8)式所示的时间转换方程来描述[13]

(8)

图1　航天器位置误差在脉冲星视线矢量上的投影

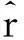
(9)

(10)

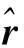
1.3周期折叠

到达航天器的X射线脉冲星信号非常微弱，受X射线探测器有效面积的限制，往往很难根据一个脉冲周期的光子到达时间观测量建立观测脉冲轮廓，而是需要对脉冲星进行多个脉冲周期的重复观测。航天器上的X射线探测器记录大量的光子到达时间观测量，并将光子到达时间通过(9)式转换到SSB，接下来，应用周期折叠方法，在SSB构造观测脉冲轮廓。

周期折叠根据以下步骤进行(如图2所示)：首先，根据光子到达时间，将所有光子到达事件排列到一条时间轴上；其次，将该时间轴折叠到一个单个的时间区间，该时间区间的长度等于1个脉冲周期；接下来，将该时间区间分割为多个具有同样长度的时间窗口，并计算在整个观测时段内落入各个时间窗口的光子数；最后，对落入各个时间窗口的光子数进行标准化处理，从而在一个单个的脉冲周期内建立观测脉冲轮廓。

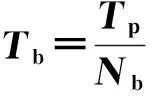
(11)

(12)

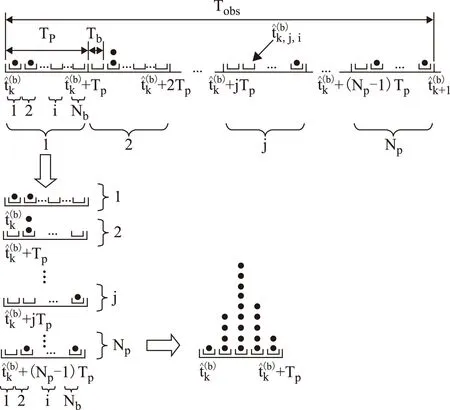
图2　周期折叠过程示意图

1.4脉冲到达时间差计算

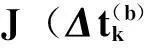
(13)

(14)

2导航性能改善

考虑到在光子到达时间观测量的时间转换过程中需要航天器的位置信息，如果航天器的位置不是精确已知的，则时间转换不能准确进行，这将导致观测脉冲轮廓波形失真。由于失真的观测脉冲轮廓和标准脉冲轮廓形状不一致，通过二者的比对计算得到的脉冲到达时间差具有较大误差。特别是对于X射线脉冲星导航系统而言，由于需要较长的观测时段来构造观测脉冲轮廓，测量更新的间隔较大，修正航天器位置信息的频率非常低，而航天器在惯性空间中的位置是时变的，如果仅依赖X射线脉冲星导航系统进行初始定位，则初始化时间较长。针对这一问题，本文提出，融合X射线探测器和光学敏感器的测量信息，建立“脉冲星+光学”组合导航系统。将光学测量信息引入自主导航系统，相当于为X射线脉冲星导航提供了中等精度的先验位置信息，能够克服航天器初始位置误差的影响，优化时间转换和脉冲叠加的处理过程，改善脉冲到达时间差测定精度，为实现航天器快速高精度高可靠自主导航奠定基础[14-15]。

星光角距是典型的光学导航观测量之一，定义为地心方向矢量和恒星方向矢量的夹角，如图3所示。

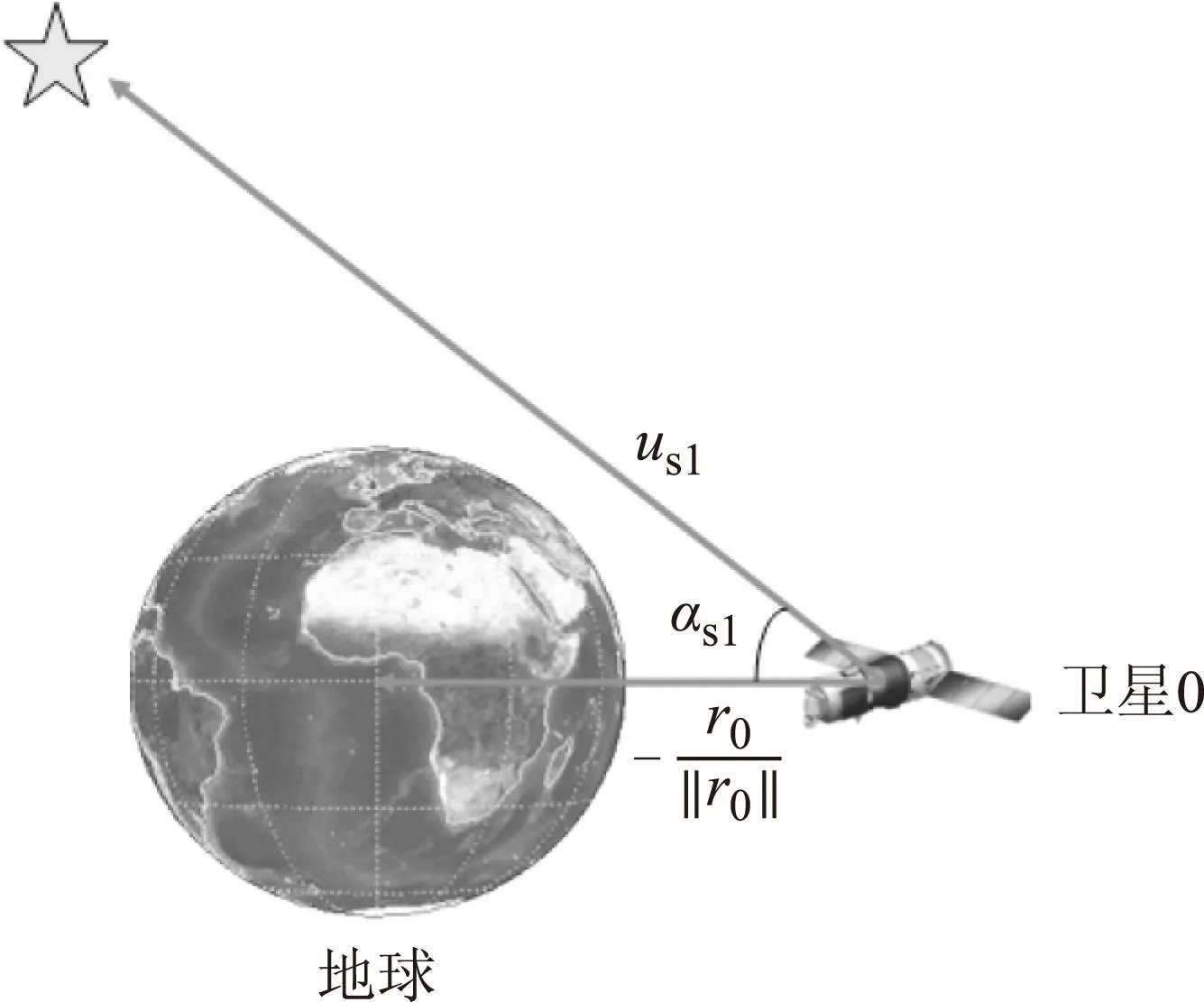
图3　星光角距观测量

图3中，us1是恒星方向矢量，-r0/‖r0‖是地心方向矢量。北京控制工程研究所研制的紫外导航敏感器是一种先进的光学敏感器，采用光机电一体化结构，能够实现对地球和恒星的同时同探测器成像，集成了地球敏感器和星敏感器的功能。采用紫外导航敏感器可以直接从成像信息中提取出导航所需的星光角距观测量，避免导航精度受平台姿态误差或敏感器相对安装误差的影响。

紫外导航敏感器的测量方程为

yu,k=hu(xk)+vu,k

(15)

式(15)中，

(16)

(17)

yu,k表示紫外导航系统的观测量，状态变量xk为航天器的位置矢量和速度矢量在地心惯性系的3个分量，vu,k表示测量噪声，αsj是星光角距，usj(j=1，2)是恒星方向矢量，下标j用于区分不同的恒星。应用过程中，通过观测多颗恒星有助于提高导航精度。

在“脉冲星+光学”组合导航系统中，通过扩展卡尔曼滤波(extended Kalman filter，EKF)算法处理脉冲星和光学导航观测量，获取航天器位置和速度的最优估计值。选择航天器位置和速度矢量作为状态变量，X射线探测器提供的脉冲到达时间差和紫外导航敏感器提供的星光角距作为观测量，EKF算法基于简化的航天器轨道动力学模型，以及测量方程(8)式和(15)式进行设计。基于EKF的信息融合算法如式(18)～式(22)所示。

时间更新为

(18)

(19)

测量更新为

(20)

(21)

(22)

图4　“脉冲星+光学”信息融合策略

“脉冲星+光学”组合导航系统的信息融合策略如图4所示，其运行流程包括光子TOA和星光角矩测量、时间转换、周期折叠、脉冲到达时间差计算，以及信息融合和位置估计等步骤。一方面，脉冲到达时间差信息用于EKF解算，估计航天器的位置和速度；另一方面，EKF估计结果用于光子TOA数据处理，以获得脉冲到达时间差观测量。在组合导航系统中，信号处理和导航解算的过程密切联系，不可分割。组合导航系统的特色在于：将光学敏感器测量信息引入脉冲星原始信号的闭环处理过程，辅助建立时间转换方程，对X射线光子到达时间数据进行时间转换。引入紫外导航敏感器测量信息的主要优势在于：能够在航天器先验位置误差较大的情况下获得清晰稳定的观测脉冲轮廓，提高脉冲到达时间差的计算精度，对航天器自主导航系统提供高精度的观测量，从而提升自主导航性能。

3仿真结果

本节通过数值仿真分析基于“脉冲星+光学”的组合导航方法的性能。假定航天器在近圆轨道上围绕地球飞行，轨道半长轴为7 471 km，轨道倾角为63°。设置航天器初始位置和速度误差分别为50 km和50 m/s。用于导航的2颗X射线脉冲星分别为B0531+21和B1821-24。仅利用1台X射线探测器进行导航，采用分时段观测2颗脉冲星的方式，假定X射线探测器转在2维指向机构上，可实现对导航脉冲星的跟踪观测，设观测周期为200 s。脉冲速率常数设为λb=5 ph/s和λs=10 ph/s。假定星光角距测量精度为0.02°，仿真时间为5个观测周期。

将通过周期折叠和脉冲轮廓比对得到的脉冲到达时间差观测量用于航天器自主导航，脉冲到达时间差计算和导航解算迭代进行，通过EKF得到的航天器位置误差曲线如图5所示。图中实线表示航天器位置误差，虚线表示EKF估计误差矩阵相应对角元的平方根。不难看出，脉冲星导航性能受到航天器初始误差的显著影响，导航滤波在仿真过程中未收敛。

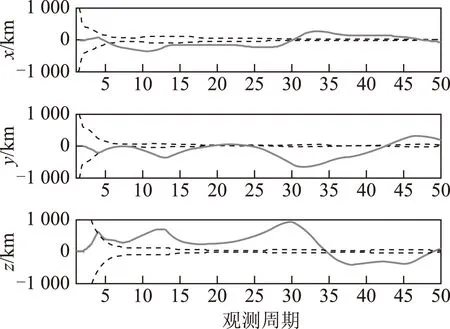
图5　脉冲星导航位置估计误差曲线

通过周期折叠方法得到的脉冲星B1821-24的观测脉冲轮廓如图6所示。图中实线表示观测脉冲轮廓，虚线表示标准脉冲轮廓。受初始位置和速度误差的影响，波形出现了明显的失真。采用失真的波形进行轮廓比对，将影响脉冲到达时间差测定精度，并进一步影响状态估计和自主导航精度。

图6　观测脉冲轮廓与标准脉冲轮廓比对(XNAV)

将紫外导航敏感器提供的光学导航信息引入脉冲星导航系统，得到的组合导航位置估计误差曲线如图7所示。相对单独采用脉冲星导航而言，组合导航系统性能得到了显著改善，导航滤波快速收敛，状态估计误差曲线在EKF方差规定的误差界范围内，能够达到km级的精度水平。

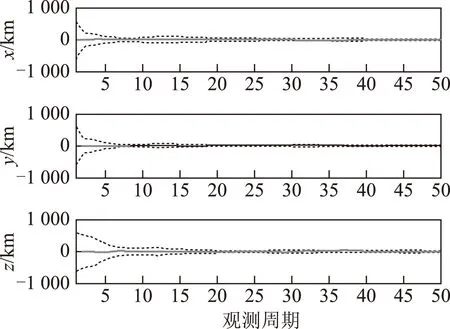
图7　组合导航位置估计误差曲线

此时，脉冲星B1821-24的观测脉冲轮廓和标准脉冲轮廓如图8所示，观测脉冲轮廓在波形上接近标准脉冲轮廓，此时通过轮廓比对能够获得较为精确的脉冲到达时间差。上述仿真结果说明所设计的基于“脉冲星+光学”的组合导航方法是有效的。

图8　观测脉冲轮廓与标准脉冲轮廓比对(组合导航)

4结束语

X射线脉冲星导航系统的信号处理和观测量提取过程中需要用到航天器的位置信息，因此，存在导航性能易受航天器初始误差影响的问题。在航天器初始位置和速度误差较大的情况下，单独采用脉冲星导航方式难以在短时间内获得理想的导航精度。针对这一问题，本文提出通过“脉冲星+光学”的组合导航方式来提升脉冲到达时间差观测量的测定精度。与现有工作相比，本文方法的主要特色在于，将紫外导航敏感器提供的中等精度的测量信息用于优化脉冲星光子到达时间信号的闭环处理过程，以获得清晰稳定的脉冲波形。所提方法的优势在于能够在航天器初始误差较大的情况下，显著改善X射线脉冲星导航系统的性能，实现快速高精度自主导航。

参考文献

[1]FANG J，NING X.Installation direction analysis of star sensors by hybrid condition number[J].IEEE Transactions on Instrumentation and Measurement，2009，58(10)：3576-3582.

[2]SHEIKH S I，PINES D J，RAY P S，et al.Spacecraft navigation using X-ray pulsars[J].Journal of Guidance，Control and Dynamics，2006，29(1)：49-63.

[3]XIONG K，WEI C L，LIU L D.The use of X-ray pulsars for aiding navigation of satellites in constellations[J].Acta Astronautica，2009，64(4)：427-436.

[4]DU J，FEI B，LIU Y，et al.Application of STEKF in X-ray pulsar based autonomous navigation[J].Procedia Engineering，2012，29(4)：4369-4373.

[5]LIU J，MA J，TIAN J，et al.Pulsar navigation for interplanetary mission using CV model and ASUKF[J].Aerospace Science and Technology，2012，22(1)：19-23.

[6]DENG X P，HOBBS G，YOU X P，et al.Interplanetary spacecraft navigation using pulsars[J].Advances in Space Research，2013，52(9)：1602-1621.

[7]WANG Y，ZHENG W，SUN S，et al.X-ray pulsar-based navigation system with the errors in the planetary ephemerides for earth-orbiting satellite[J].Advances in Space Research，2013，51(12)：2394-2404.

[8]WEI E，JIN S，ZHANG Q，et al.Autonomous navigation of mars probe using X-ray Pulsars：modeling and results[J].Advances in Space Research，2013，51(5)：849-857.

[9]EMADZADEH A A，SPEYER J L.On modeling and pulse phase estimation of X-ray pulsars[J].IEEE Transactions on Signal Processing，2010，58(9)：4484-4495.

[10]RINAURO S，COLONNESS S，SCARANO G.Fast near-maximum likelihood phase estimation of X-ray pulsars[J].Signal Processing，2013，93(1)：326-331.

[11]ZHANG H，XU L，SONG S，et al.Fast method for X-ray pulsar signal simulation[J].Acta Astronautica，2014，98(5)：189-200.

[12]LI S L，LIU K，XIAO L L.Fleet algorithm for X-ray pulsar profile construction and TOA solution based on compressed sensing[J].Optik，2014，125(7)：1875-1879.

[13]费保俊，孙维瑾，潘高田，等.X射线脉冲星自主导航的光子到达时间转换[J].空间科学学报，2010，30(1)：85-90.

[14]杨成伟，郑建华，李明涛.基于脉冲星和太阳敏感器的日地系Halo轨道组合导航研究[J].北京理工大学学报，2013，33(6)：612-616.

[15]杨成伟，郑建华，高东.基于脉冲星和紫外敏感器的自主定轨定姿授时研究[J].空间科学学报，2013，33(2)：194-199.

Performance Enhancement of X-ray Pulsar Navigation Based on Optical Sensor

XIONGKai，WEIChunling

(Science and Technology on Space Intelligent Control Laboratory，Beijing Institute of Control Engineering，Beijing 100190，China)

Abstract：This paper studies the X-ray pulsar-based navigation (XNAV) method for spacecrafts based on the difference between the measured and predicated pulse arrival times，which is calculated by comparing an observed pulse profile with a standard pulse profile in practice.It is specified that the performance of the XNAV system may be degraded in the presence of spacecraft orbit error.To cope with this problem，a novel navigation scheme is presented by integrating the autonomous optical navigation and the XNAV.The XNAV/optical integrated navigation system is effective to enhance the navigation performance in the case that the spacecraft orbit error is rather large.The superiority of the presented integrated navigation method is illustrated through numerical simulations.

Key words：autonomous navigation；X-ray pulsar；optical navigation；phase estimation；spacecraft

中图分类号：P228

文献标识码：A

文章编号：2095-4999(2016)-01-0038-06

作者简介：第一熊凯(1976—)，男，北京人，高级工程师，主要从事航天器自主导航和姿态确定方面的研究工作。

基金项目：国家973计划(2013CB733100)；重点实验室基金(9140C590201130C59213)。

收稿日期：2015-06-12

引文格式：熊凯，魏春岭.基于光学敏感器增强脉冲星导航系统性能[J].导航定位学报，2016，4(1)：38-43.(XIONG Kai，WEI Chunling.Performance Enhancement of X-ray Pulsar Navigation Based on Optical Sensor[J].Journal of Navigation and Positioning，2016，4(1)：38-43.)DOI：10.16547/j.cnki.10-1096.20160108.