基于最差性能最优的水下目标定位方法研究

周　旋，邹海英，唐　弢，孟玲龙，路喜平，宋海岩

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)



基于最差性能最优的水下目标定位方法研究

周旋，邹海英，唐弢，孟玲龙，路喜平，宋海岩

(黑龙江工程学院 电气与信息工程学院,黑龙江 哈尔滨 150050)

摘要：浅海多途环境下的水下目标定位问题一直以来是研究热点，但大多数现有方法受不精确的海洋环境及信道参数信息的影响，稳健性能严重退化，限制其在实际工程中的进一步应用。针对以上问题，基于射线理论模型，结合最差性能最优自适应波束形成处理器，提出一种稳健的水下目标定位方法，利用最差性能最优(Worst-Case Optimization)和二阶锥规划的概念，有效地克服算法对水下环境参数(海水深度、海底反射系数等)的依赖性，提高算法的稳健性，并通过计算机仿真验证该方法的正确性和有效性。

关键词：目标定位；稳健；最差性能最优；二阶锥规划

目标定位是阵列信号处理的重要研究内容，广泛应用于雷达、声纳、通信、医学成像等军用及民用领域。众多优秀的空间谱估计算法广泛应用于各个研究领域，其中水下目标定位就是重要的应用领域之一，并取得了丰硕成果[1]。然而，随着人们对水下声传播理论的逐渐认识，发现在浅海多途条件下，单纯的基于平面波模型的定位方法已经不能满足实际情况的要求，多途效应会使定位算法出现很大的误差，甚至使算法失效。为了对水下声源进行准确的定位，出现了大量的结合实际水声信道特性进行声源定位的方法。匹配场处理(MFP)就是用于波导中源定位的经典方法[2-5]。Lakshmipathi等人提出了一种新的子空间正交高分辨算法，用于浅海中的信号入射方位角估计[6]。张爱民等人基于浅海简正波模型，利用最小二乘子空间相交方法进行浅海目标方位的估计[7]。候云山等人同样采用简正波声场理论，推导了方位角的最大似然估计公式[8]。

虽然学者们已经做了大量的研究，但大多数浅海声源定位方法在实际应用中面临着一个共同的问题：稳健性问题，即要求精确获取海洋环境及信道的参数，例如：海底沉积层的声学特性、海底空间变化特性、海底反射系数、海水声速、海水深度等信息，不精确的海洋环境及信道信息将使算法的性能严重退化，产生很大的定位误差。然而，在实际的情况下，通常只能获得水声环境及信道参数的近似值，这必将严重影响算法的性能[9]。

针对以上问题，本文以高频声信号近程定位为工程背景，在浅海多途条件下，基于射线理论模型，提出一种稳健的水下声源定位方法。该算法实际上是在无限多个非凸二次约束条件下进行二次函数优化的问题，首先将非凸优化问题转化成二阶锥规划(Second Order Corn Programming，SOCP)问题，再通过优化工具SeDuMi进行有效求解[10]。理论分析和计算机仿真表明，本文提出的声源定位方法对声传播模型具有很强的鲁棒性，对信道及环境参数等不确定性因素具有很好的宽容性，具体地说，就是对海底反射系数、海洋信道深度、阵型扰动等参数的不确定性具有较强的稳健性，同时算法执行效率高，具有应用于实际工程的光明前景。

1阵列信号模型

图1　浅海水平线阵阵列信号模型

阵列信号模型如图1所示，考虑深度为Hm的均匀Pekeris信道[11]，垂直接收平面阵置于水下hrm处，声源置于水下hsm处且与垂直阵水平距离Rm。定义声源入射的方位角为θ，俯仰角为φ及水平距离为R，假设对基阵接收信号有意义的虚源个数为M。第i个基元接收的信号可表示为

(1)

考虑噪声的影响，平面阵接收到的信号矢量可以表示为

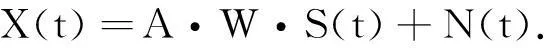
(2)

其中：

式中：A为镜像空间，W为加权系数，B=A·W为源矢量，式(2)即为浅海多途条件下的阵列信号模型。

2基于最差性能最优的稳健水下目标定位方法

2.1基于最差性能最优的稳健方法原理

考虑源矢量误差Δ的影响，将源矢量B重新表达为如下形式：

(3)

则实际的源矢量B将属于下面的集合：

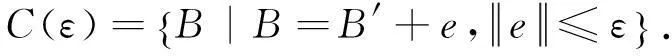
(4)

对属于集合C(ε)的源矢量进行约束，即阵列响应的绝对值不小于1：

(5)

因此，稳健算法可以表示成约束最优问题：

(6)

其中，Rtrue为严格意义上的统计量。通过化简，可得式(6)等价形式：

(7)

式(7)与不确定集的表达形式相似[12]。该方法的主要目的是解决由于源矢量误差而引起的算法性能下降的问题；同时，由于B′中不包含水深、海底反射系数等参数，故该方法对这些参数具有很强的稳健性。为方便起见，称表达式(7)为最小方差稳健定位算法(Minimum Variance robust algorithm，MV-robust)。

2.2基于矢量最优化的稳健算法求解

根据正则化方法[13]，式(7)可等效为：

(8)

(9)

令

(10)

(11)

(12)

(13)

则式(9)可表式成二阶锥形式：

(14)

至此，可将式(8)的优化问题转化成式(14)的二阶锥优化问题，利用SeDuMi软件可以方便地进行求解[10]。

3计算机仿真分析

在本文的仿真中，信噪比和阵型扰动的定义分别为

信噪比定义：

阵型扰动定义：

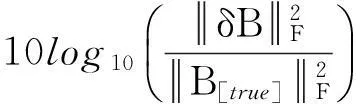
3.1仿真分析单声源方位估计结果

信号频率f=200 kHz，平面阵y轴方向阵元个数9个，z轴方向阵元个数9个，取平面阵中心基元为坐标原点，阵元间距半波长，采样快拍数1 024×10(6.4 ms)，水深15 m，声源入水深度5 m，接收基阵入水深度5 m，声源距基阵的水平距离R为8倍水深，声源入射方位角25°。海水声速1 500 m/s，密度1.0 g/cc，海底声速1 700 m/s，密度2.0 g/cc。阵型扰动-5 dB，信噪比20 dB。方位角扫描范围[20°:1°:30°]，深度扫描范围[2:1:13]，约束参数0.7，仿真结果如图2所示。

(a) 常规处理器估计结果

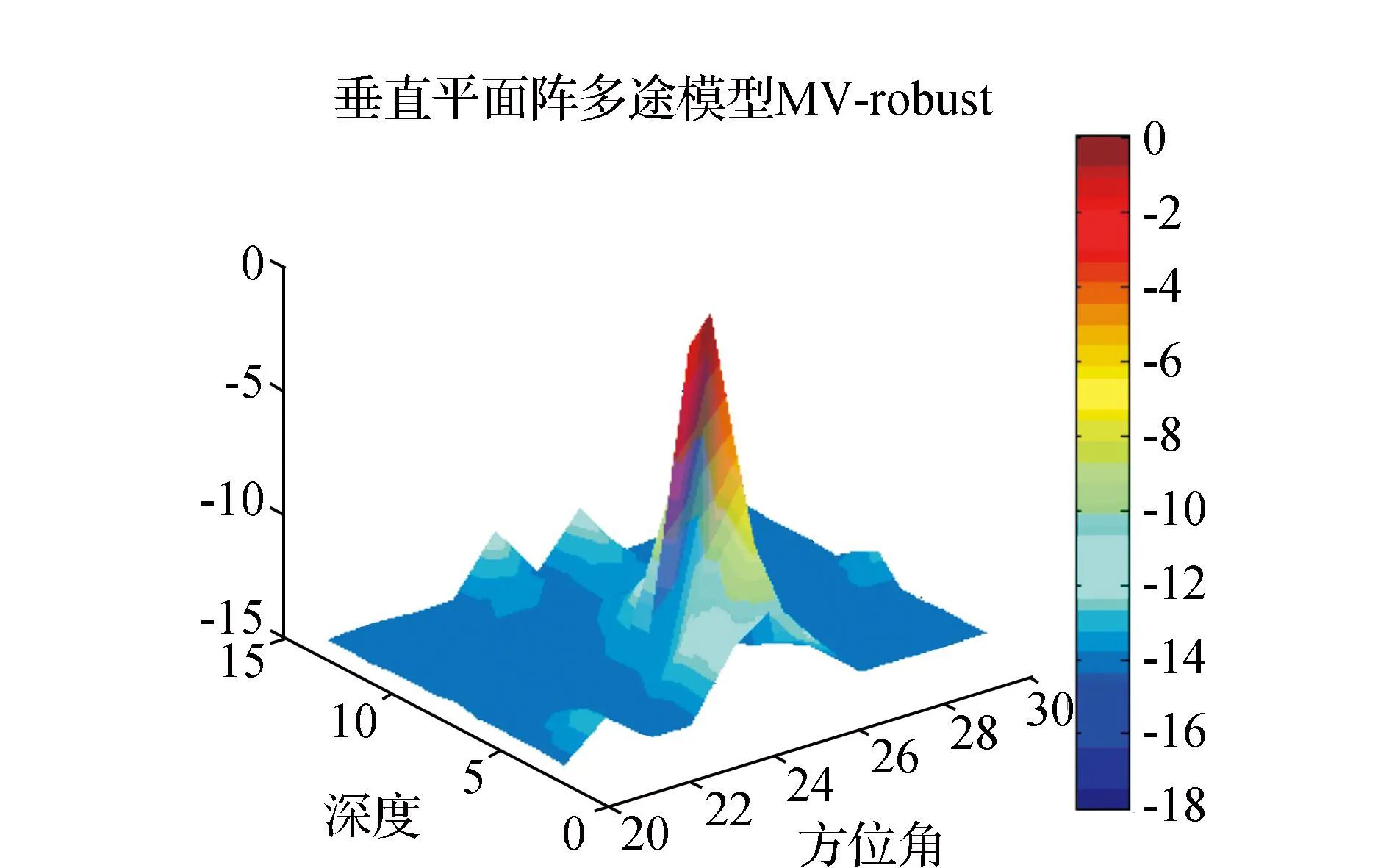
(b) MV-robust估计结果图2　单声源方位估计结果

图2(a)为常规处理器估计的结果，图2(b)为最小方差稳健法(MV-robust)估计的结果。比较两种方法的仿真结果可以看出，常规方法的分辨率较低，尤其是深度分辨率，并且旁瓣级的起伏较大，不利于目标的检测，虚警概率高；MV-robust算法的分辨力明显高于常规算法，与常规算法相比，不仅主瓣峰值尖锐，而且旁瓣级较低，有利于对目标的检测，大大提高了目标的检测概率。

3.2仿真分析相干源方位估计结果

两相干信号频率f=200 kHz，平面阵y轴方向阵元个数11个，z轴方向阵元个数11个，取平面阵中心基元为坐标原点，阵元间距半波长，采样快拍数1 024×10(6.4 ms)，水深15 m，声源1入水深度5 m，声源2入水深度6 m，接收基阵入水深度5 m，声源距基阵的水平距离R为8倍水深，声源1入射方位角25°，声源2入射方位角27°。海水声速1 500 m/s，密度1.0 g/cc，海底声速1 700 m/s，密度2.0 g/cc。方位角扫描范围[20°:1°:30°]，深度扫描范围[2:1:13]，阵型扰动-5 dB，信噪比20 dB，约束参数0.9，仿真结果如图3所示。

图3(a)为常规处理器估计的结果，图3(b)为MV-robust估计的结果。比较两种方法的仿真结果可以看出，常规方法的分辨率较差，旁瓣的起伏较大；MV-robust算法分辨率明显高于常规方法，能够清晰辨别两个相干源目标，并且旁瓣级较低，有利于信号的检测。

3.3仿真分析算法性能

3.3.1海底沉积层特性对估计结果的影响

信号频率f=200 kHz，平面阵y轴方向阵元个数9个，z轴方向阵元个数9个，取平面阵中心基元为坐标原点，阵元间距半波长，采样快拍数1 024×10(6.4 ms)，水深15 m，声源入水深度5 m，接收基阵入水深度5 m，声源距基阵的水平距离R为2倍水深，声源入射方位角25°。海水密度1.0 g/cc，海水声速1 500 m/s。阵型扰动-5 dB，信噪比20 dB。

方位角扫描范围[20°:1°:30°]，深度扫描范围[2:1:13]，约束参数0.7。表1给出了不同海底地质条件下，分别用常规方法和MV-robust估计声源深度和方位角的统计结果。

(a) 常规处理器估计结果

(b) MV-robust估计结果图3　相干源方位估计结果

表1　不同海底地质条件下估计声源的深度和方位角

从表1的统计结果可以看出，常规方法和MV-robust算法对声源深度和方位的估计结果都很准确，但MV-robust算法估计结果的空间谱峰值明显高于常规算法，说明其稳健性更强。从表中还可以看出，不同沉积层条件下，本文MV-robust算法估计的空间谱峰基本保持不变，说明其受海底沉积层声学特性的影响较小。

3.3.2信噪比对估计结果的影响

仿真条件：信号频率f=200 kHz，平面阵y轴方向阵元个数9个，z轴方向阵元个数9个，取平面阵中心基元为坐标原点，阵元间距半波长，采样快拍数1 024×10(6.4 ms)，水深15 m，声源入水深度5 m，接收基阵入水深度5 m，声源距基阵的水平距离R为2倍水深，声源入射方位角25°。海水密度1.0 g/cc，海水声速1 500 m/s，沉积层密度2.0 g/cc，沉积层声速1 700 m/s。阵型扰动-5 dB。方位角扫描范围[20°:1°:30°]，深度扫描范围[2:1:13]，约束参数0.7。表2给出了不同信噪比条件下，分别用常规方法和MV-robust算法估计声源深度和方位角的统计结果。

表2　不同信噪比条件下估计声源的深度和方位角

从表2的统计结果可以看出，信噪比在0～50 dB范围内，常规方法和MV-robust算法对声源深度和方位的估计结果都很准确，但MV-robust算法估计结果的空间谱峰值明显高于常规算法，说明其稳健性更强。从表中还可以看出，随着信噪比逐渐降低，本文MV-robust算法估计的空间谱峰值逐渐变小，说明在较低的信噪比条件下，MV-robust算法的性能有所下降。

4结束语

在浅海环境下，由于声传播多途效应的影响，导致传统的方位估计算法存在较大的估计偏差，在某些情况下，甚至会导致谱峰分裂。从理论上来说，完全知道水声传播的信道及环境参数才有可能对声源进行准确可靠的定位。但是，在大多数实际情况下，根本无法准确地得到这些参数，这样就使得估计结果不稳定，甚至使估计方法失效。根据以上情况，本文建立了符合水声传播特点的阵列模型，研究了一种稳健的浅海高分辨声源定位方法，该方法基于最差性能最优和二阶锥规划的概念，对信道及环境参数等不确定性因素具有很强的宽容性。计算机仿真给出了本文方法对单声源及相干源估计的结果，同时分析了算法对不同的海底沉积层及信噪比的稳健性能，充分验证了该方法的有效性，同时为该方法的工程实用化奠定了理论基础。

参考文献

[1]TUNCER E,FRIEDLANDER B. Classical and Modern Direction-of-Arrival Estimation[M]. Elsevier, 2009.8.

[2]DOSSOA S E,WILMUT M J. Bayesian tracking of multiple acoustic sources in an uncertain ocean environment. J. Acoust. Soc. Am., 2013, 133(4): EL274-EL280.

[3]SEONG W,BYUN S H. Robust matched field-processing algorithm based on feature extraction[J].IEEE J. Oceanic ENG., 2002,27:642-652.

[4]YANG T C. Data-based matched-mode source localization for a moving source[J]. J. Acoust. Soc. Am., 2014, 135(3): 1218-1230.

[5]SNELLEN M, SIMONS D G.An evaluation of the accuracy of shallow water matched field inversion results[J], J. Acoust. Soc. Am., 2001,109(2):514-527.

[6]LAKSHMIPATHI S, ANAND G V. Subspace intersection method of high-resolution bearing estimation in shallow ocean[J]. Signal Processing, 2004,84:1367-1384.

[7]张爱民, 林京, 黄晓砥. 最小二乘子空间相交方法用于浅海目标方位估计[J]. 哈尔滨工程大学学报, 2006, 27(1):1-4.

[8]侯云山, 黄建国, 张立杰, 等. 一种新的浅海目标方位估计方法[J]. 西安交通大学学报, 2008, 42(10):1295-1299.

[9]舒象兰, 韩树平, 孙荣光, 等. 声传播多途效应对目标方位估计影响的仿真研究[J]. 舰船科学技术, 2009, 31(9):121-124.

[10] STURM J F. Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones[J]. Optim Meth Softw, 1999, 11:625-653.

[11] SHI J, YANG D S, SHI S G. A robust localization and identification method of noise sources using second-order cone programming[J]. Journal of Harbin Engineering University. 2011, 32(12):1549-1555.

[12] VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust Adaptive Beamforming Using Worst-Case Performance Optimization: A Solution to the Signal Mismatch Problem[C]. IEEE Transactions on Signal Processing, 2003, 51(2):313-324.

[13] 李鹏飞. Tikhonov正则法在解决不适定问题的应用[D]. 济南：山东大学, 2009.

[责任编辑：郝丽英]

Underwater source localization in shallow water based on worst-case optimization

ZHOU Xuan, ZOU Haiying, TANG Tao, MENG Linglong, LU Xiping, SONG Haiyan

(College of Electrical and Information Engineering, Heilongjiang Institute of Technology, Harbin 150050, China)

Abstract：Due to the multipath effect, the source localization in shallow water has been an area of active interest. However, most methods for source localization in shallow water are sensitive to the assumed model of the underwater environment and have poor robustness against the underwater channel uncertainty, which limit their further application to practical engineering. In this paper, a new method of source localization in shallow water, based on worst-case optimization concept, is proposed, which is highly robust against environmental factors affecting the localization, such as the channel depth, the bottom reflection coefficients, and so on. Through constructing the uncertainty set of the source vector errors and only extracting a direct sound and a reflected sound from the sea surface, the proposed method can accurately localize one or more sources in shallow water dominated by multipath propagation. Computer simulations show better performance of the proposed method as compared with existing algorithms and establish a theoretical foundation for the practical engineering application.

Key words：source localization in shallow water; robust; worst-case optimization; second-order cone programming

中图分类号：TN911.7

文献标识码：A

文章编号：1671-4679(2016)01-0035-05

作者简介：周旋(1994-)，男，本科生，研究方向：现代信号处理．

基金项目：黑龙江省青年科学基金项目(QC2014C079)；黑龙江省普通本科高等学校青年创新人才培养计划(UNPYSCT-2015101)；黑龙江工程学院大学生创新训练项目(201411802039)

收稿日期：2015-10-19